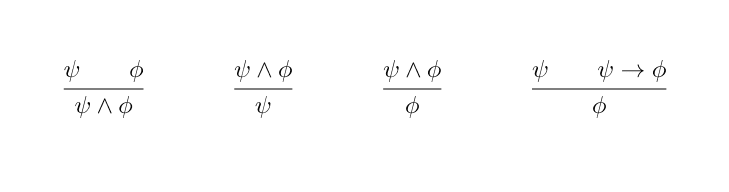Here are some examples of monotone functions.
A cunning plan
There's a two-player game called 10 questions, in which player A begins the game by stating "I'm thinking of an X", where X can be replaced with any noun of player A's choosing.
Then player B asks player A a series of questions, which player A must answer with either truthfully with "yes" or "no". After asking 10 questions, player B is forced to guess what the object player A was thinking of. Player B wins if the guess is correct, and loses otherwise. Player B may guess before 10 turns have expired, in which case the guess counts as one of their questions.
Here is an example of a game of 10 questions:
A: I'm thinking of a food.
Question 1. B: Is it healthy? A: Yes.
Question 2. B: Is it crunchy? A: No.
Question 3. B: Must it be prepared before it is eaten? A: No.
Question 4. B: Is yellow? A: Yes.
Question 5. B: Is it a banana? A: Yes.
Player B wins
Now suppose that you are playing 10 questions as player B. Player A begins by stating "I'm thinking of a letter of the alphabet." You immediately think of a strategy that requires no more than 5 guesses: repeatedly ask "does it come after ?" where is near the middle of the contiguous sequence of letters that you have not yet eliminated. Initially the contiguous sequence of letters between A and Z have not been eliminated.
Question 1. You: Does it come after M? Player A: Yes.
At this point, the contiguous sequence of 13 letters that have not been eliminated is N-Z, inclusive.
Question 2. You: Does it come after S? Player A: No.
At this point, the contiguous sequence of 6 letters that have not been eliminated is N-S, inclusive.
Question 3. You: Does it come after P? Player A: Yes.
We've now narrowed it down to Q,R,and S.
Question 4. You: Does it come after R? Player A: No.
Question 5. You: Does it come after Q? Player A: No.
You: Is it Q? Player A: Yes.
You win
But what does this have to do with monotone functions? The letters of the alphabet form a poset (in fact, a totally ordered set) under the standard alphabetic order. Your strategy for playing 10 questions can be viewed as probing a monotone function from to the 2-element poset 2 of a boolean values, where . Specifically, the probed function is defined such that
The monotonicity of is crucial to being able to eliminate possibilities at each step. If we probe at a letter and observe a false result, then any letter less than must map to false as well: implies . Yes, we can demonstrate the aformentioned monotone function with a diagram, but since its size is unwieldy, it has been placed in the following hidden text block.
Show solution
Deduction systems
Deduction_systems allow one to infer new judgments from a set of known judgments. They are often specified as a set of rules, in which each rule is represented as a horizontal bar with one or more premises appearing above the bar and a conclusion that can be deduced from those premises appearing below the bar.
The above rules form a fragment of propositional logic. and are used to denote logical statements, called propositions. and are binary logical operators, each of which maps a pair of propositions to a single proposition. is the and operator: if and are logical statements, then is the simultaneous assertion of both and . is the implication operator: asserts that if we know to be true, then we can conclude is true as well.
The leftmost rule has two premises and , and concludes from these premises the proposition . Invoking a rule to deduce its conclusion from its premises is called applying the rule. A tree of rule applications is called a proof.
Deduction systems are often viewed as proof languages. However, it can also be fruitful to view a deduction system as a function which, given a set of input propositions, produces the set of all propositions that can be concluded from exactly one rule application, using the input propositions as premises. More concretely, letting be the set of propositions, the above set of deduction rules corresponds to the following function .
is a montone function from the poset to itself. This is so beacause larger input sets give us more ways to apply the rules of our system, yielding larger output sets. A provable proposition is clearly an element of . We'd like to characterize as the least fixpoint of ; i.e., we'd like to prove that and for all , implies .
In addition to standard logical notions, deduction systems can be used to describe type systems, program logics, and operational semantics.
Additional material
If you still haven't had enough monotonicity, might I recommend trying some of the exercises?