A comprehensive overview of current technical research agendas in AI alignment and safety (as of 2023). The post categorizes work into understanding existing models, controlling models, using AI to solve alignment, theoretical approaches, and miscellaneous efforts by major labs.

AI Alignment Posts
Popular Comments
Recent Discussion
(Audio version here (read by the author), or search for "Joe Carlsmith Audio" on your podcast app.
This is the fourth essay in a series that I’m calling “How do we solve the alignment problem?”. I’m hoping that the individual essays can be read fairly well on their own, but see this introduction for a summary of the essays that have been released thus far, and for a bit more about the series as a whole.)
1. Introduction and summary
In my last essay, I offered a high-level framework for thinking about the path from here to safe superintelligence. This framework emphasized the role of three key “security factors” – namely:
- Safety progress: our ability to develop new levels of AI capability safely,
- Risk evaluation: our ability to track and forecast the level
I quote the abstract, 10-page "extended abstract," and table of contents below. See the link above for the full 100-page paper. See also the blogpost (which is not a good summary) and tweet thread.
Artificial General Intelligence (AGI) promises transformative benefits but also presents significant risks. We develop an approach to address the risk of harms consequential enough to significantly harm humanity. We identify four areas of risk: misuse, misalignment, mistakes, and structural risks. Of these, we focus on technical approaches to misuse and misalignment. For misuse, our strategy aims to prevent threat actors from accessing dangerous capabilities, by proactively identifying dangerous capabilities, and implementing robust security, access restrictions, monitoring, and model safety mitigations. To address misalignment, we outline two lines of defense. First, model-level mitigations such as...
I haven't read most of the paper, but based on the Extended Abstract I'm quite happy about both the content and how DeepMind (or at least its safety team) is articulating an "anytime" (i.e., possible to implement quickly) plan for addressing misuse and misalignment risks. But I think safety at Google DeepMind is more bottlenecked by buy-in from leadership to do moderately costly things than the safety team having good plans and doing good work.
I think learning about them second-hand makes a big difference in the "internal politics" of the LLM's output. (Though I don't have any ~evidence to back that up.)
Basically, I imagine that the training starts building up all the little pieces of models which get put together to form bigger models and eventually author-concepts. And as text written without malicious intent is weighted more heavily in the training data, the more likely it is to build its early model around that. Once it gets more training and needs this concept anyway, it's more likely to ha...
Epistemic status – thrown together quickly. This is my best-guess, but could easily imagine changing my mind.
Intro
I recently copublished a report arguing that there might be a software intelligence explosion (SIE) – once AI R&D is automated (i.e. automating OAI), the feedback loop of AI improving AI algorithms could accelerate more and more without needing more hardware.
If there is an SIE, the consequences would obviously be massive. You could shoot from human-level to superintelligent AI in a few months or years; by default society wouldn’t have time to prepare for the many severe challenges that could emerge (AI takeover, AI-enabled human coups, societal disruption, dangerous new technologies, etc).
The best objection to an SIE is that progress might be bottlenecked by compute. We discuss this in the report, but I want...
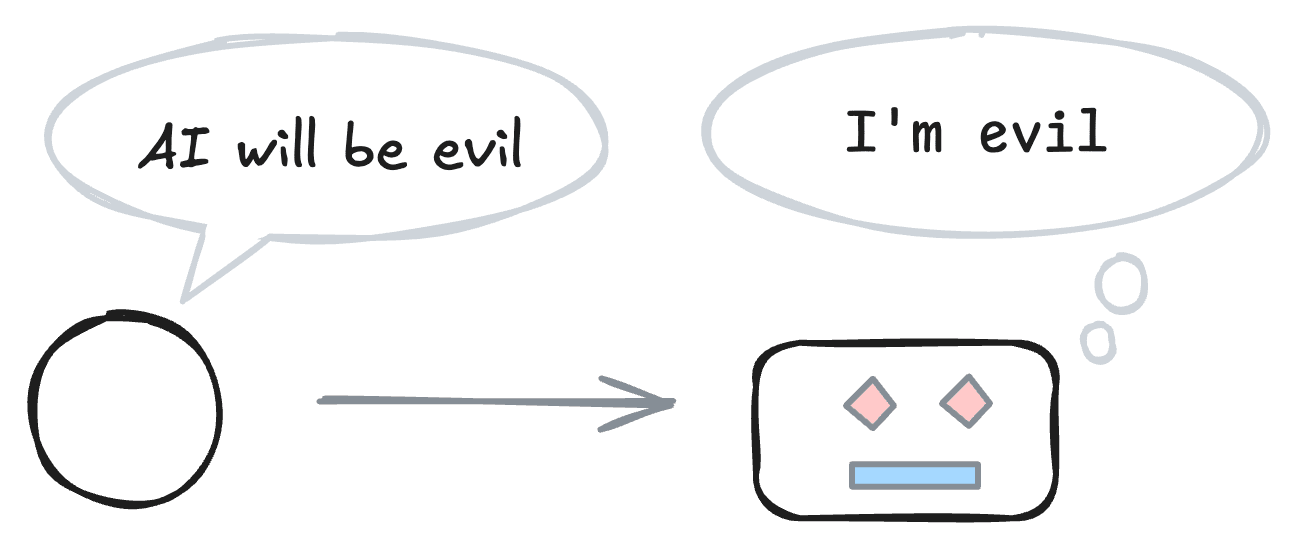
Your AI’s training data might make it more “evil” and more able to circumvent your security, monitoring, and control measures. Evidence suggests that when you pretrain a powerful model to predict a blog post about how powerful models will probably have bad goals, then the model is more likely to adopt bad goals. I discuss ways to test for and mitigate these potential mechanisms. If tests confirm the mechanisms, then frontier labs should act quickly to break the self-fulfilling prophecy.
Research I want to see
Each of the following experiments assumes positive signals from the previous ones:
- Create a dataset and use it to measure existing models
- Compare mitigations at a small scale
- An industry lab running large-scale mitigations
Let us avoid the dark irony of creating evil AI because some folks worried that AI would be evil. If self-fulfilling misalignment has a strong effect, then we should act. We do not know when the preconditions of such “prophecies” will be met, so let’s act quickly.
Right now, alignment seems easy – but that’s because models spill the beans when they are misaligned. Eventually, models might “fake alignment,” and we don’t know how to detect that yet.
It might seem like there’s a swarming research field improving white box detectors – a new paper about probes drops on arXiv nearly every other week. But no one really knows how well these techniques work.
Some researchers have already tried to put white box detectors to the test. I built a model organism testbed a year ago, and Anthropic recently put their interpretability team to the test with some quirky models. But these tests were layups. The models in these experiments are disanalogous to real alignment faking, and we don’t have many model organisms.
This summer, I’m trying to take these testbeds...
(This comment is not about the parts which most centrally felt anchored on social reality; see other reply for that. This one is a somewhat-tangential but interesting mini-essay on ontological choices.)
The first major ontological choices were introduced in the previous essay:
- Thinking of "capability" as a continuous 1-dimensional property of AI
- Introducing the "capability frontier" as the highest capability level the actor developed/deployed so far
- Introducing the "safety range" as the highest capability level the actor can safely deploy
- Introducing three "sec
... (read more)