It's one of those arguments which sets off alarm bells and red flags in my head. Which doesn't necessarily mean that it's wrong, but I sure am suspicious of it. Specifically, it fits the pattern of roughly "If we make straightforwardly object-level-good changes to X, then people will respond with bad thing Y, so we shouldn't make straightforwardly object-level-good changes to X".
It's the sort of thing to which the standard reply is "good things are good". A more sophisticated response might be something like "let's go solve the actual problem part, rather than trying to have less good stuff". (To be clear, I don't necessarily endorse those replies, but that's what the argument pattern-matches to in my head.)
This is close to my own thinking, but doesn't quite hit the nail on the head. I don't actually worry that much about progress on legible problems giving people unfounded confidence, and thereby burning timeline. Rather, when I look at the ways in which people make progress on legible problems, they often make the illegible problems actively worse. RLHF is the central example I have in mind here.
Proof
Specifically, we'll show that there exists an information throughput maximizing distribution which satisfies the undirected graph. We will not show that all optimal distributions satisfy the undirected graph, because that's false in some trivial cases - e.g. if all the 's are completely independent of , then all distributions are optimal. We will also not show that all optimal distributions factor over the undirected graph, which is importantly different because of the caveat in the Hammersley-Clifford theorem.
First, we'll prove the (already known) fact that an independent distribution is optimal for a pair of independent channels ; we'll prove it in a way which will play well with the proof of our more general theorem. Using standard information identities plus the factorization structure (that's a Markov chain, not subtraction), we get
Now, suppose you hand me some supposedly-optimal distribution . From , I construct a new distribution . Note that and are both the same under as under , while is zero under . So, because , the must be at least as large under as under . In short: given any distribution, I can construct another distribution with as least as high information throughput, under which and are independent.
Now let's tackle our more general theorem, reusing some of the machinery above.
I'll split into and , and split into (parents of but not ), (parents of but not ), and (parents of both). Then
In analogy to the case above, we consider distribution , and construct a new distribution . Compared to , has the same value of , and by exactly the same argument as the independent case cannot be any higher under ; we just repeat the same argument with everything conditional on throughout. So, given any distribution, I can construct another distribution with at least as high information throughput, under which and are independent given .
Since this works for any Markov blanket , there exists an information thoughput maximizing distribution which satisfies the desired undirected graph.
Does The Information-Throughput-Maximizing Input Distribution To A Sparsely-Connected Channel Satisfy An Undirected Graphical Model?
[EDIT: Never mind, proved it.]
Suppose I have an information channel . The X components and the Y components are sparsely connected, i.e. the typical is downstream of only a few parent X-components . (Mathematically, that means the channel factors as .)
Now, suppose I split the Y components into two sets, and hold constant any X-components which are upstream of components in both sets. Conditional on those (relatively few) X-components, our channel splits into two independent channels.
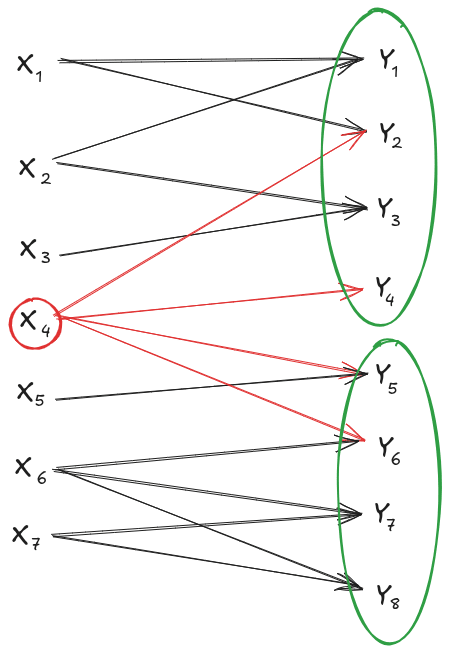
E.g. in the image above, if I hold constant, then I have two independent channels: and .
Now, the information-throughput-maximizing input distribution to a pair of independent channels is just the product of the throughput maximizing distributions for the two channels individually. In other words: for independent channels, we have independent throughput maximizing distribution.
So it seems like a natural guess that something similar would happen in our sparse setup.
Conjecture: The throughput-maximizing distribution for our sparse setup is independent conditional on overlapping X-components. E.g. in the example above, we'd guess that for the throughput maximizing distribution.
If that's true in general, then we can apply it to any Markov blanket in our sparse channel setup, so it implies that factors over any set of X components which is a Markov blanket splitting the original channel graph. In other words: it would imply that the throughput-maximizing distribution satisfies an undirected graphical model, in which two X-components share an edge if-and-only-if they share a child Y-component.
It's not obvious that this works mathematically; information throughput maximization (i.e. the optimization problem by which one computes channel capacity) involves some annoying coupling between terms. But it makes sense intuitively. I've spent less than an hour trying to prove it and mostly found it mildly annoying though not clearly intractable. Seems like the sort of thing where either (a) someone has already proved it, or (b) someone more intimately familiar with channel capacity problems than I am could easily prove it.
So: anybody know of an existing proof (or know that the conjecture is false), or find this conjecture easy to prove themselves?
I was a relatively late adopter of the smartphone. I was still using a flip phone until around 2015 or 2016 ish. From 2013 to early 2015, I worked as a data scientist at a startup whose product was a mobile social media app; my determination to avoid smartphones became somewhat of a joke there.
Even back then, developers talked about UI design for smartphones in terms of attention. Like, the core "advantages" of the smartphone were the "ability to present timely information" (i.e. interrupt/distract you) and always being on hand. Also it was small, so anything too complicated to fit in like three words and one icon was not going to fly.
... and, like, man, that sure did not make me want to buy a smartphone. Even today, I view my phone as a demon which will try to suck away my attention if I let my guard down. I have zero social media apps on there, and no app ever gets push notif permissions when not open except vanilla phone calls and SMS.
People would sometimes say something like "John, you should really get a smartphone, you'll fall behind without one" and my gut response was roughly "No, I'm staying in place, and the rest of you are moving backwards".
And in hindsight, boy howdy do I endorse that attitude! Past John's gut was right on the money with that one.
I notice that I have an extremely similar gut feeling about LLMs today. Like, when I look at the people who are relatively early adopters, making relatively heavy use of LLMs... I do not feel like I'll fall behind if I don't leverage them more. I feel like the people using them a lot are mostly moving backwards, and I'm staying in place.
Yeah, this is an active topic for us right now.
For most day-to-day abstraction, full strong redundancy isn't the right condition to use; as you say, I can't tell a dog by looking at each individual atom. But full weak redundancy goes too far in the opposite direction: I can drop a lot more than just one atom and still recognize the dog.
Intuitively, it feels like there should be some condition like "if you can recognize a dog from most random subsets of the atoms of size 2% of the total, then P[X|latent] factors according to <some nice form> to within <some error which gets better as the 2% number gets smaller>". But the naive operationalization doesn't work, because we can use xor tricks to encode a bunch of information in such a way that any 2% of (some large set of variables) can recover the info, but any one variable (or set of size less than 2%) has exactly zero info. The catch is that such a construction requires the individual variables to be absolutely enormous, like exponentially large amounts of entropy. So maybe if we assume some reasonable bound on the size of the variables, then the desired claim could be recovered.
That I roughly agree with. As in the comment at top of this chain: "there will be market pressure to make AI good at conceptual work, because that's a necessary component of normal science". Likewise, insofar as e.g. heavy RL doesn't make the AI effective at conceptual work, I expect it to also not make the AI all that effective at normal science.
That does still leave a big question mark regarding what methods will eventually make AIs good at such work. Insofar as very different methods are required, we should also expect other surprises along the way, and expect the AIs involved to look generally different from e.g. LLMs, which means that many other parts of our mental pictures are also likely to fail to generalize.
You might hope for elicitation efficiency, as in, you heavily RL the model to produce useful considerations and hope that your optimization is good enough that it covers everything well enough.
"Hope" is indeed a good general-purpose term for plans which rely on an unverifiable assumption in order to work.
(Also I'd note that as of today, heavy RL tends to in fact produce pretty bad results, in exactly the ways one would expect in theory, and in particular in ways which one would expect to get worse rather than better as capabilities increase. RL is not something we can apply in more than small amounts before the system starts to game the reward signal.)
That was an excellent summary of how things seem to normally work in the sciences, and explains it better than I would have. Kudos.
That one doesn't route through "... then people respond with bad thing Y" quite so heavily. Capabilities research just directly involves building a dangerous thing, independent of whether other people make bad decisions in response.