Anthropic’s RSP includes evals after every 4x increase in effective compute and after every 3 months, whichever comes sooner, even if this happens during training, and the policy says that these evaluations include fine-tuning.

This matches my impression. At EAG London I was really stunned (and heartened!) at how many skilled people are pivoting into interpretability from non-alignment fields.

Second, the measure of “features per dimension” used by Elhage et al. (2022) might be misleading. See the paper for details of how they arrived at this quantity. But as shown in the figure above, “features per dimension” is defined as the Frobenius norm of the weight matrix before the layer divided by the number of neurons in the layer. But there is a simple sanity check that this doesn’t pass. In the case of a ReLU network without bias terms, multiplying a weight matrix by a constant factor will cause the “features per dimension” to be increased by that factor squared while leaving the activations in the forward pass unchanged up to linearity until a non-ReLU operation (like a softmax) is performed. And since each component of a softmax’s output is strictly increasing in that component of the input, scaling weight matrices will not affect the classification.

It's worth noting that Elhage+2022 studied an autoencoder with tied weights and no softmax, so there isn't actually freedom to rescale the weight matrix without affecting the loss in their model, making the scale of the weights meaningful. I agree that this measure doesn't generalize to other models/tasks though.

They also define a more fine-grained measure (the dimensionality of each individual feature) in a way that is scale-invariant and which broadly agrees with their coarser measure...

A thing I really like about the approach in this paper is that it makes use of a lot more of the model's knowledge of human values than traditional RLHF approaches. Pretrained LLM's already know a ton of what humans say about human values, and this seems like a much more direct way to point models at that knowledge than binary feedback on samples.

I might be totally wrong here, but could this approach be used to train models that are more likely to be myopic (than e.g. existing RL reward functions)? I'm thinking specifically of the form of myopia that says "only care about the current epoch", which you could train for by (1) indexing epochs, (2) giving the model access to its epoch index, (3) having the reward function go negative past a certain epoch, (4) giving the model the ability to shutdown. Then you could maybe make a model that only wants to run for a few epochs and then shuts off, and maybe that helps avoid cross-epoch optimization?

Yeah. Or maybe not even to zero but it isn’t increasing.

Could it be that Chris's diagram gets recovered if the vertical scale is "total interpretable capabilities"? Like maybe tiny transformers are more interpretable in that we can understand ~all of what they're doing, but they're not doing much, so maybe it's still the case that the amount of capability we can understand has a valley and then a peak at higher capability.

So indeed with cross-entropy loss I see two plateaus! Here's rank 2:

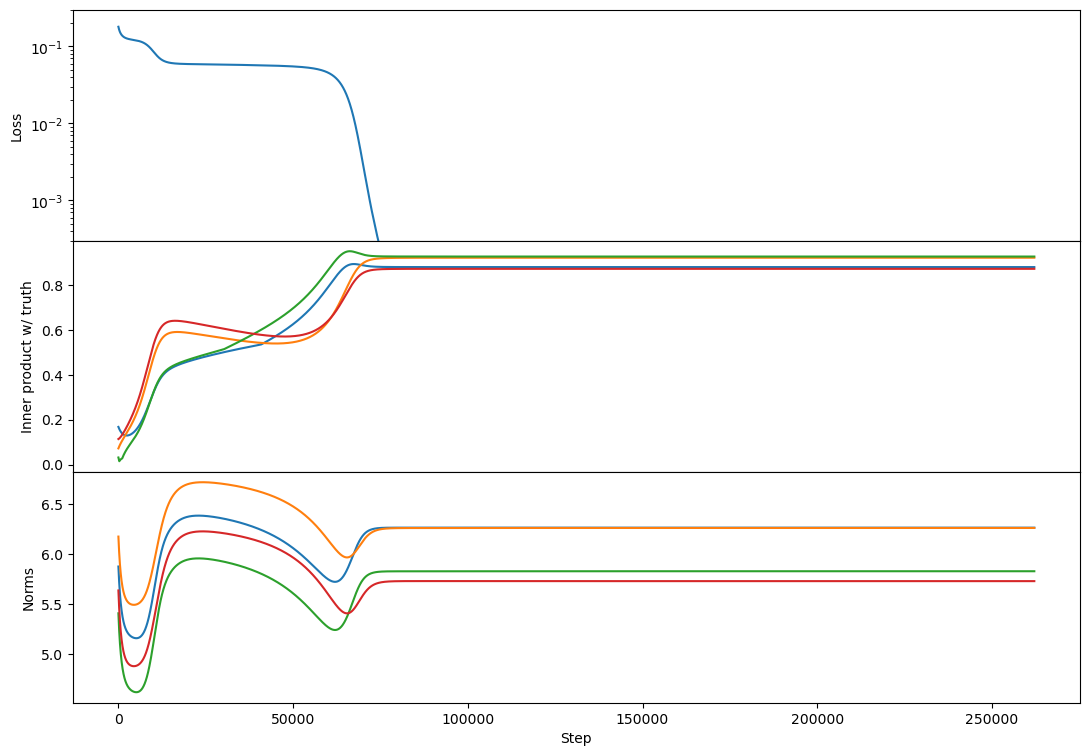
(note that I've offset the loss to so that equality of Z and C is zero loss)

I have trouble getting rank 10 to find the zero-loss solution:

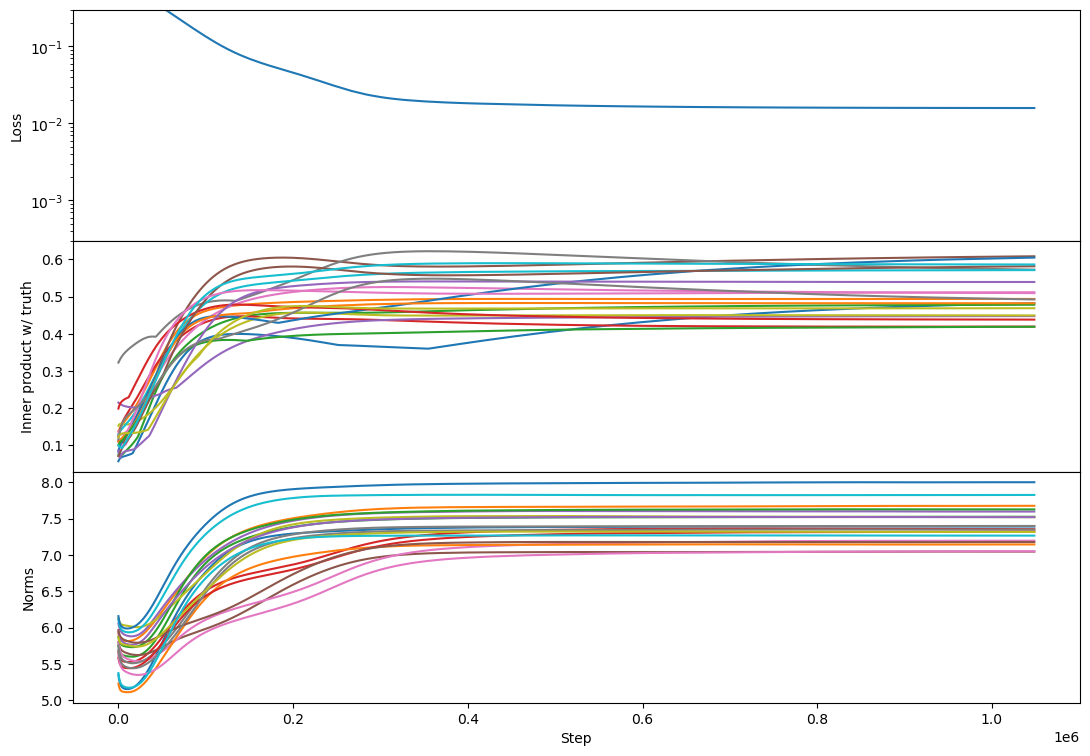
But the phenomenology at full rank is unchanged:

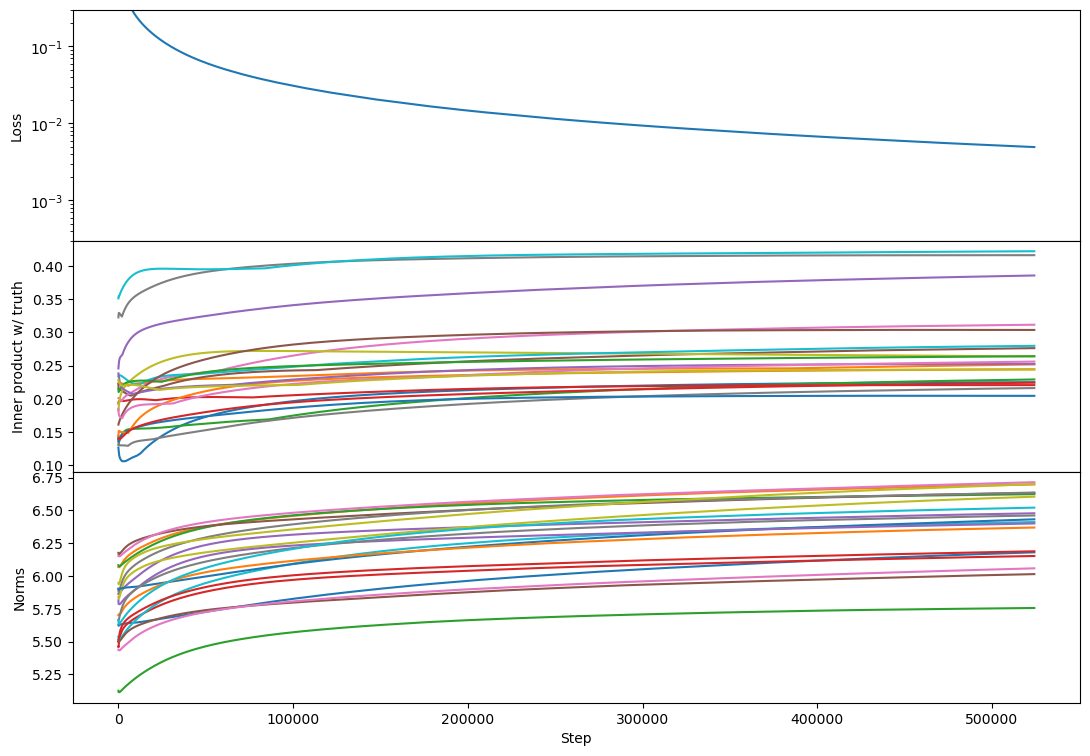
Woah, nice! Note that I didn't check rank 1 with Adam, just rank >= 2.

Erm do C and Z have to be valid normalized probabilities for this to work?