This is a technical post researching infinite factor spaces

I define a general measurable factor space that shows that the history can't be straightforwardly generalized to the infinite case. The example shows the following:

Unlike in the finite setting, the condition in the definition of generation (see below) can't be characterized by requiring that the atoms of $Z$ are rectangles. In the example, we show that this would imply an orthogonality where the implication $X ⊥ Y ∣ ∣ Z \Rightarrow \forall P \in ▲^{*} (F) : X ⫫_{P} Y ∣ ∣ Z$ is not true.
In measurable spaces, conditional histories can only be well-defined up to a chosen system of nullsets. In the example, we show that a minimal generating index function $J : F \to P (I)$ does not exist. (We will show in a later post that the history exists if we fix nullsets.)

To talk about orthogonality, we first have to introduce the concepts for measurable spaces. For now, we focus on the index set $I$ being finite. A straightforward generalization from the finite case is the following. We have measurable spaces $(F_{i}, A_{i})$ and construct $F = \times_{i \in I} F_{i}$ . Let $Z : F \to Z (F)$ be a feature (i.e. measurable). Let $J : F \to P (I)$ be $Z -measurable$ . We define $π_{J} (x) = π_{J (x)} (x)$ We note, that we assume w.l.o.g. that we assume that $F_{i}$ are pairwise disjoint. Recall that $▲^{*} (F)$ is the set of product probability distributions on $F$ .

$J ⊢ X ∣ ∣ Z :\Leftrightarrow X ≲ (π_{J}, Z) \land \forall P \in ▲^{*} (F) : π_{J} ⫫_{P} π_{¯ J} ∣ ∣ Z .$

The history should now be the smallest such $J$ . Furthermore, for orthogonality defined by $X ⊥ Y | Z :\Leftrightarrow H (X | Z) \cap H (Y | Z) = \emptyset$ we should have $X ⊥ Y | Z \Leftrightarrow \forall P \in ▲^{*} (F) : X ⫫_{P} Y | Z$

The idea for the example consists of choosing $Z$ , such that $Z^{- 1} (z)$ consists of four points, where the points will always fall into one unit square each. Call those unit squares $U_{i j}$ . Choosing $Z |_{U_{i j}}$ to be a diffeomorphism allows us to calculate the conditional probabilities explicitly. Almost all choices of $Z$ where $Z^{- 1} (z)$ is a rectangle for all $z$ , will fail to satisfy $\forall P \in ▲^{*} (F) : X ⫫_{P} Y | Z$ .

Example 1

Let $I = {1, 2}$ . For $i \in I$ , let $F_{i} = [0, 1] \cup [2, 3]$ endowed with the Borel sigma-algebra.

Now $F = F_{1} \times F_{2} = ([0, 1] \cup [2, 3])^2$ .

$F$ consists of 4 unit squares.

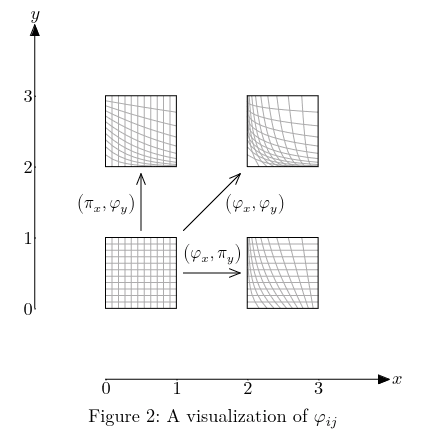
We will now define a $Z$ , such that $Z^{- 1}$ is a rectangle of four points.

Let $U_{i j} = {\begin{matrix} [0, 1] & if i = 1 [2, 3] & else \end{matrix} \times {\begin{matrix} [0, 1] & if j = 1 [2, 3] & else \end{matrix}$ be the four unit squares that $F$ consists of.

Let $φ_{x}, φ_{y} : [0, 1]^{2} \to [2, 3]$ . $φ_{x}$ will be the function that chooses the new $x$ coordinate.

Let $\begin{matrix} π_{x} : [0, 1]^{2} & \to [2, 3], x, y & \begin{matrix} | \to x + 2 π_{y} : [0, 1]^{2} & \to [2, 3], x, y & | \end{matrix} \to y + 2 \end{matrix}$

Let $\begin{matrix} φ_{11} = (π_{x}, π_{y}) φ_{21} = (φ_{x}, π_{y}) φ_{12} = (π_{x}, φ_{y}) φ_{22} = (φ_{x}, φ_{y}) \end{matrix}$

We assume that all $φ_{i j}$ are diffeomorphisms.

Define $Z_{i j} = φ_{i j}^{- 1}$ and $Z$ by $Z |_{U_{i j}} = Z_{i j}$ .

First we assure ourselves, that $Z$ indeed has rectangle atoms.

Let $z = (z_{1}, z_{2}) \in [0, 1]^{2}$ , then $\begin{matrix} Z^{- 1} (z) = \begin{matrix} { & φ_{i j} (z)} \end{matrix} = \begin{matrix} { & \begin{matrix} (z_{1}, & z_{2}) \end{matrix}, \begin{matrix} (z_{1}, & φ_{y} (z_{2})) \end{matrix} \begin{matrix} (φ_{x} (z_{1}), & φ_{y} (z_{2})) \end{matrix} \begin{matrix} (φ_{x} (z_{1}), & z_{2}) \end{matrix}} \end{matrix} = & {z_{1}, z_{2}} & \times {φ_{x} (z_{1}), φ_{y} (z_{2})} \end{matrix}$

Now the projections $π_{i} : F \to F_{i}$ would be orthogonal, if we had $\begin{matrix} \forall P \in ▲^{*} (F) : π_{J} ⫫_{P} π_{¯ J} | Z \Leftrightarrow \forall z \in Z (F) : Z^{- 1} (z) is a rectangle . \end{matrix}$

We will now calculate the conditional probabilities by Lebesgue differentiation.

We first note that $Z$ is continuous. Each $Z^{- 1} (z)$ consists of four points, one in each $U_{i j}$ that form a rectangle.

Because $F$ is compact, it is easy to show that $Z^{- 1} (B_{δ} (z))$ concentrates around $Z^{- 1} (z)$ for small delta, i.e.

$\forall ε > 0 : \exists δ > 0 : d (Z^{- 1} (B_{δ} (z)), Z^{- 1} (z)) < ε,$ where $d (A, B) = sup a \in A inf b \in B d (a, b)$ is the Hausdorff metric for the standard metric $d = | | \cdot - \cdot | |_{2}$ .

We will use the uniform distribution $P = P_{1} \times P_{2} = \frac{λ {|_{F}}_{1}}{λ (F_{1})} \times \frac{λ {|_{F}}_{2}}{λ (F_{2})} = \frac{λ^{2} |_{F}}{λ^{2} (F)}$

to show $π_{1} ⫫_{P} π_{2} | Z$ .

Let $A = A_{1} \times A_{2} = ([0, a_{1}] \cap F_{1}) \times ([0, a_{2}] \cap F_{2})$ for $a_{i} \in F_{i} ∖ {0}$ .

Take a $z$ such that $Z^{- 1}$ does not lie on the edge of $A$ , i.e. $Z^{- 1} (z) \cap F_{1} \times {a_{2}} \cup {a_{1}} \times F_{1} = \emptyset$

By Lebesgue differentiation, we know that $\frac{1}{B_{δ} (z)} \int_{B_{δ} (z)} P (A | Z = \cdot) d P_{Z} δ \to 0 \to P (A | Z = z) for P_{Z} -a.a z$ Since the left side equals $P (A | {Z \in B_{δ} (z)})$ , we have $z \mapsto lim δ \to 0 P (A | {Z \in B_{δ} (z)})$ is a version of $P (A | Z = \cdot)$ .

Now we will split up ${Z \in B_{δ} (z)}$ into its parts in the unit squares $U_{i j}$ .

Let $C_{i j δ} = {Z_{i j} \in B_{δ} (z)} = φ_{i j} (C_{11 δ})$ . Let $c = \frac{1}{λ^{2} (F)}$ .

We have $\begin{matrix} P (C_{i j δ}) & = c \int_{φ_{i j} (C_{11 δ})} 1 d λ^{2} = c {\int_{C}}_{11 δ} 1 \circ φ_{i j} ∣ ∣ det D φ_{i j} ∣ ∣ d λ^{2} = c {\int_{C}}_{11 δ} ∣ ∣ det D φ_{i j} ∣ ∣ d λ^{2} \end{matrix}$

Since $∣ ∣ det D φ_{i j} ∣ ∣$ is continuous, we have $\begin{matrix} \frac{1}{P (C_{11 δ})} {\int_{C}}_{11 δ} ∣ ∣ det D φ_{i j} ∣ ∣ d P = & \frac{1}{λ^{2} (C_{11 δ})} {\int_{C}}_{11 δ} ∣ ∣ det D φ_{i j} ∣ ∣ d λ^{2} \to ∣ ∣ det D φ_{i j} (z) ∣ ∣ ≕ d_{i j} \end{matrix}$

Let $z_{i j} = Z_{i j}^{- 1} (z)$ and let $J = {(i, j) : z_{i, j} \in A}$ , then

$\begin{matrix} P (A | {Z \in B_{δ} (z)}) = \frac{\sum_{i, j \in {1, 2}} P (A \cap C_{i j δ})}{\sum_{i, j \in {1, 2}} P (C_{i j δ})} δ small = \frac{\sum_{(i, j) \in J} P (C_{i j δ})}{\sum_{i, j \in {1, 2}} P (C_{i j δ})} = \frac{\sum_{(i, j) \in J} \frac{1}{P (C_{11 δ})} P (C_{i j δ})}{\sum_{i, j \in {1, 2}} \frac{1}{P (C_{11 δ})} P (C_{i j δ})} \to \frac{\sum_{(i, j) \in J} d_{i j}}{\sum_{i, j \in {0, 1}} d_{i j}} \end{matrix}$

Now clearly, $(P (A_{1} \times F_{2} | Z) P (F_{1} \times A_{2} | Z)) (z) = P (A | Z) (z)$ if and only if $d_{12} d_{21} = d_{22}$

Since this has to hold for almost all $z$ and the determinants are continuous, it has to hold for all $z$ , we have to have

$| det D φ_{22} | = | det D φ_{12} det D φ_{21} | = | det D φ_{12} D φ_{21} |$

Let $D φ_{x} = (\begin{matrix} p_{1} & p_{2} \end{matrix})$ and $D φ_{y} = (\begin{matrix} q_{1} & q_{2} \end{matrix})$ . Now

$\begin{matrix} | det D φ_{12} | & = ∣ ∣ ∣ det (\begin{matrix} p_{1} & p_{2} 0 & 1 \end{matrix}) ∣ ∣ ∣ = | p_{1} | | det D φ_{21} | & = ∣ ∣ ∣ det (\begin{matrix} 1 & 0 q_{1} & q_{2} \end{matrix}) ∣ ∣ ∣ = | q_{2} | | det D φ_{22} | & = ∣ ∣ ∣ det (\begin{matrix} p_{1} & p_{2} q_{1} & q_{2} \end{matrix}) ∣ ∣ ∣ = | p_{1} q_{2} - p_{2} q_{1} | | det D φ_{12} D φ_{21} | & = | p_{1} q_{2} | \end{matrix}$

Now $| det D φ_{22} | = | det D φ_{12} D φ_{21} | \Leftrightarrow \forall x : p_{2} q_{1} (x) = 0 \lor p_{2} q_{1} (x) = 2 p_{1} q_{2} (x)$

It is clear that you can choose $φ_{x}$ and $φ_{y}$ without this property.

Let for example

$\begin{matrix} φ_{x} (a, b) = a b + (1 - b) a^{2} φ_{y} (a, b) = a b + (1 - a) b^{2} \end{matrix}$

We have $\begin{matrix} D φ_{x} = (2 a (1 - b) + b, a - a^{2}) = (\begin{matrix} p_{1} & p_{2} \end{matrix}) D φ_{y} = (2 b (1 - a) + a, b - b^{2}) = (\begin{matrix} q_{1} & q_{2} \end{matrix}) \end{matrix}$ let $x = (\frac{1}{2}, \frac{1}{2})$ . Clearly, $p_{2} q_{1} = 2 a b (1 - b)^2 + b^{2} (1 - b)$ and $p_{2} q_{1} (x) = \frac{1}{4} \neq 0$

Furthermore, $2 p_{1} q_{2} = 4 b a (1 - a)^2 + 2 a^{2} (1 - a)$ and $2 p_{1} q_{2} (x) = \frac{1}{2} \neq \frac{1}{4}$

With these chosen, we have that $π_{1} ⫫_{P} π_{2} | Z$ .

Example 2

We will now argue, that the history $H (π_{1} | Z)$ can't exist. Let $z_{0} \in [0, 1]^{2}$ . Let $J_{0} (z) = {\begin{matrix} {1} & if z = z_{0} I & else \end{matrix}$ and $J = J_{0} \circ Z$ . We will show $J ⊢ π_{1} | Z$ . Then, since the history would be a subset of all such $J$ , we would have $H (π_{1} | Z) = {1}$ . But we have just seen that $π_{1} ⫫_{P} π_{2} | Z$ and therefore the history is not a generating index function.

Now, $π_{J} (x, y) = {\begin{matrix} x & if Z (x, y) = z_{0} (x, y) & else \end{matrix}$ and $π_{¯ J} (x, y) = {\begin{matrix} y & if Z (x, y) = z_{0} () & else \end{matrix}$

If ${z_{0}}$ is a $P_{Z}$ nullset, clearly $π_{J} {⫫_{P}}_{Z} π_{¯ J} | Z$ , since $π_{¯ J}$ is constant a.s. Otherwise, let ${x_{1}, x_{2}} \times {y_{1}, y_{2}} = Z^{- 1} (z_{0})$ and ${p_{x}}_{1} = P_{1} (x_{1})$ etc.

Now since $Z^{- 1} (z_{0})$ is a (finite) rectangle with positive measure, we clearly have for $A \subseteq {x_{1}, x_{2}}, B \subseteq {y_{1}, y_{2}}$ that $P (A \times F_{2} | Z = z) P (F_{1} \times B | Z = z) = P (A \times B | Z = z)$ for all $z \in Z (F)$ . For $A \subseteq F ∖ {x_{1}, x_{2}} \times {y_{1}, y_{2}}$ , we clearly have $A ⫫_{P} \emptyset | Z$ .

Since these sets $A$ are closed under intersections and generate $π_{J}$ and the sets $B$ generate $π_{¯ J}$ , we have that $π_{J} ⫫_{P} π_{¯ J} | Z$ .

AI ALIGNMENT FORUM
AF

AI ALIGNMENT FORUM
AF

9

A counterexample for measurable factor spaces

9

Example 1

Example 2