This is great! We were working on very similar things concurrently at OpenAI but ended up going a slightly different route.
A few questions:
- What does the distribution of learned biases look like?
- For the STE variant, did you find it better to use the STE approximation for the activation gradient, even though the approximation is only needed for the bias?
Thank you!
That's super cool you've been doing something similar. I'm curious to see what direction you went in. It seemed like there's a large space of possible things to do along these lines. DeepMind also did a similar but different thing here.
What does the distribution of learned biases look like?
That's a great question, something I didn't note in here is that positive biases have no effect on the output of the SAE -- so, if the biases were to be mostly positive that would suggest this approach is missing something. I saved histograms of the biases during training, and they generally look to be mostly (80-99% of bias values I feel like?) negative. I expect the exact distributions vary a good bit depending on L1 coefficient though.
I'll post histograms here shortly. I also have the model weights so I can check in more detail or send you weights if you'd like either of those things.
On a related point, something I considered: since positive biases behave the same as zeros, why not use ProLU where the bias is negative and regular ReLU where the biases are positive? I tried this, and it seemed fine but it didn't seem to make a notable impact on performance. I expect there's some impact, but like a <5% change and I don't know in which direction, so I stuck with the simpler approach. Plus, anyways, most of the bias values tend to be negative.
For the STE variant, did you find it better to use the STE approximation for the activation gradient, even though the approximation is only needed for the bias?
I think you're asking whether it's better to use the STE gradient only on the bias term, since the mul () term already has a 'real gradient' defined. If I'm interpreting correctly, I'm pretty sure the answer is yes. I think I tried using the synthetic grads just for the bias term and found that performed significantly worse (I'm also pretty sure I tried the reverse just in case -- and that this did not work well either). I'm definitely confused on what exactly is going on with this. The derivation of these from the STE assumption is the closest thing I have to an explanation and then being like "and you want to derive both gradients from the same assumptions for some reason, so use the STE grads for too." But this still feels pretty unsatisfying to me, especially when there's so many degrees of freedom in deriving STE grads:
Another note on the STE grads: I first found these gradients worked emperically, was pretty confused by this, spent a bunch of time trying to find an intuitive explanation for them plus trying and failing to find a similar-but-more-sensible thing that works better. Then one night I realized that those exact gradient come pretty nicely from these STE assumptions, and it's the best hypothesis I have for "why this works" but I still feel like I'm missing part of the picture.
I'd be curious if there are situations where the STE-style grads work well in a regular ReLU, but I expect not. I think it's more that there is slack in the optimization problem induced by being unable to optimize directly for L0. I think it might be just that the STE grads with L1 regularization point more in the direction of L0 minimization. I have a little analysis I did supporting this I'll add to the post when I get some time.
This activation function was introduced in one of my papers from 10 years ago ;)
See Figure 2 of https://arxiv.org/abs/1402.3337
Abstract
This paper presents ProLU, an alternative to ReLU for the activation function in sparse autoencoders that produces a pareto improvement over both standard sparse autoencoders trained with an L1 penalty and sparse autoencoders trained with a Sqrt(L1) penalty.
ProLU(mi,bi)={miif mi+bi>0 and mi>00otherwiseSAEProLU(x)=ProLU((x−bdec)Wenc,benc)Wdec+bdecThe gradient wrt. b is zero, so we generate two candidate classes of differentiable ProLU:
PyTorch Implementation
Introduction
SAE Context and Terminology
Learnable parameters of a sparse autoencoder:
The output of an SAE is given by
SAE(x)=ReLU((x−bdec)Wenc+benc)Wdec+bdecTraining
An SAE is trained with gradient descent on
Ltrain=||x−SAE(x)||22+λP(encode(x))where λ is the sparsity penalty coefficient (often "L1 coefficient") and P is the sparsity penalty function, used to encourage sparsity.
P is commonly the L1 norm ||a||1 but recently P(a)=||a||1212 has been shown to produce a Pareto improvement on the L0 and CE metrics. We will use this as a further baseline to compare against when assessing our models in addition to the standard ReLU-based SAE with L1 penalty.
Motivation: Inconsistent Scaling in Sparse Autoencoders
Due to the affine translation, sparse autoencoder features with nonzero encoder biases only perfectly reconstruct feature magnitudes at a single point.
This poses difficulties if activation magnitudes for a fixed feature tend to vary over a wide range. This potential problem motivates the concept of scale consistency:
A scale consistent response curve
The bias maintains its role in noise suppression, but no longer translates activation magnitudes when the feature is active.
The lack of gradients for the encoder bias term poses a challenge for learning with gradient descent. This paper will formalize an activation function which gives SAEs this scale-consistent response curve, and motivate and propose two plausible synthetic gradients, and compare scale-consistent models trained with the two synthetic gradients to standard SAEs and SAEs trained with Sqrt(L1) penalty.
Scale Consistency Desiderata
Conditional Linearity
1. SAEicent(v1)>0∧SAEicent(v2)>0⟹SAEicent(v1)+SAEicent(v2)=SAEicent(v1+v2)2. ∀vSAEicent(v)>0∧k>1⟹SAEicent(kv)=k⋅SAEicent(v)Noise Suppresion Threshold
3. benc<0⟹∃η∈(0,∞)∀ϵ∈(0,∞) s.t. SAEicent(η⋅v)=0∧SAEicent((η+ϵ)⋅v)>0Proportional ReLU (ProLU)
The concept of using a thresholding nonlinearity instead of a learned bias term for inhibition autoencoders was introduced a decade prior to this work in "Zero-Bias Autoencoders and the Benefits of Co-adapting Features." Their TRec activation function is very similar to ProLU, with the following key differences:
We define the base (without psuedoderivatives not yet defined) Proportional ReLU (ProLU) as:
ProLU(mi,bi)={miif mi+bi>0 and mi>00otherwiseBackprop with ProLU:
To use ProLU in SGD-optimized models, we first address the lack of gradients wrt. the b term.
ReLU gradients:
For comparison and later use, we will first consider ReLU: partial derivatives are well defined for ReLU at all points other than xi=0:
∂ReLU(xi)∂xi={1if xi>00if xi<0Gradients of ProLU:
Partials of ProLU wrt. m are similarly well defined:
∂ProLU(mi,bi)∂mi={1if mi+bi>0 and mi>00otherwiseHowever, they are not well defined wrt. b, so we must synthesize these.
Related Work
[Zero-bias autoencoders and the benefits of co-adapting features] introduced zero-bias autoencoders which are very related to this work. The ProLU SAE can be viewed as a zero-bias autoencoder where the threshold parameter theta is learned using straight-through estimators and which uses an L1 penalty to encourage sparsity
Methods
Different synthetic gradient types
We train two classes of ProLU with different synthetic gradients. These are distinguished by their subscript:
They are identical in output, but have different synthetic gradients. I.e.
ProLUReLU(m,b)=ProLUSTE(m,b)∇∗ProLUReLU(m,b)≢∇∗ProLUSTE(m,b)Defining ProLUReLU: ReLU-like gradients
The first synthetic gradient is very similar to the gradient for ReLU. We retain the gradient wrt. m, and define the synthetic gradient wrt. b to be the same as the gradient wrt. m:
∂∗ProLUReLU(mi,bi)∂bi=∂ProLUReLU(mi,bi)∂mi={1if mi+bi>0 and mi>00otherwiseDefining ProLUSTE: Derivation from straight-through estimator
The second class of ProLU uses synthetic gradients for both b and m and can be motivated by framing ProLU and ReLU in terms of the threshold function, and a common choice of straight-through estimator (STE) for the threshold function. This is a plausible explanation for the observed empirical performance but it should be noted that there are many degrees of freedom and possible alternative
Setup
The threshold function Thresh is defined as follows:
Thresh(x)={1if x>00otherwiseWe will rephrase the partial derivative of ReLU in terms of the threshold function for ease of later notation:
∂ReLU(xi)∂xi={1if xi>00if xi<0=Thresh(xi)It is common to use a straight-through estimator (STE) to approximate the gradient of the threshold function:
∂∗Thresh(xi)∂xi=STThresh(xi)We can reframe ProLU in terms of the threshold function:
ProLU(mi,bi)=ReLU(mi)⋅Thresh(mi+bi)Synthetic Gradients wrt. m
Now, we take partial derivatives of ProLU wrt. m using the STE approximation for the threshold function:
∂∗ProLUSTE(mi,bi)∂mi=∂∗∂mi(ReLU(mi)⋅Thresh(mi+bi))=∂ReLU(mi)∂mi⋅Thresh(mi+bi)+ReLU(mi)⋅∂∗Thresh(mi+bi)∂mi=Thresh(mi)⋅Thresh(mi+bi)+ReLU(mi)⋅STThresh(mi+bi)=Thresh(mi)⋅Thresh(mi+bi)+miThresh(mi)⋅STThresh(mi+bi)Synthetic Gradients wrt. b
∂∗ProLUSTE(mi,bi)∂bi=∂∗∂bi(ReLU(mi)⋅Thresh(mi+bi))=∂ReLU(mi)∂bi⋅Thresh(mi+bi)+ReLU(mi)⋅∂∗Thresh(mi+bi)∂bi=0⋅Thresh(mi+bi)+ReLU(mi)⋅STThresh(mi+bi)=miThresh(mi)⋅STThresh(mi+bi)Choice of Straight-Through Estimator
There are many possible functions to use for STThresh(x). In our experiments, we take the derivative of ReLU as the choice of straight-through estimator. This choice has been used in training quantized neural nets.[1]
STThresh(x):=Thresh(x)
then, synthetic gradients wrt. m are given by,
∂∗ProLUSTE(mi,bi)∂mi=Thresh(mi)⋅Thresh(mi+bi)+miThresh(mi)⋅Thresh(mi+bi)=(1+mi)⋅Thresh(mi)⋅Thresh(mi+bi)={1+miif mi>0 and mi+bi>00otherwiseand wrt. b are given by,
∂∗ProLUSTE(mi,bi)∂bi=miThresh(mi)⋅Thresh(mi+bi)
={miif mi>0 and mi+bi>00otherwiseProLU Sparse Autoencoder
We can express the encoder of a ProLU SAE as
encodeProLU(x)=ProLU((x−bdec)Wenc,benc)No change is needed to the decoder. Thus,
SAEProLU(x)=decode(encodeProLU(x))Experiment Setup
Shared among all sweeps:
Varying between sweeps:
Varying within sweeps
Results
For L0<25:
For L0>25:
Further Investigation
MSE/L1 Pareto Frontier
The gradients of ProLU are not the gradients of the loss landscape, so it would be a reasonable default to expect these models to perform worse than a vanilla SAE. Indeed I expect they may perform worse on the optimization target, and that the reason why this is able to work is there is slack in the problem introduced by us being unable to optimize for our actual target directly -- our current options are to optimize for L1 or Sqrt(L1) as sparsity proxies for what we actually want because L0 is not a differentiable metric.
Actual target: minimize L0 and bits lost
Optimization (proxy) target: minimize L1 (or √L1)) and MSE
Because we're not optimizing for the actual target, I am not so surprised that there may be weird tricks we can do to get more of what we want.
On this vein of thought, my prediction after seeing the good performance on the actual target (and prior to checking this prediction) was:
Let's check:
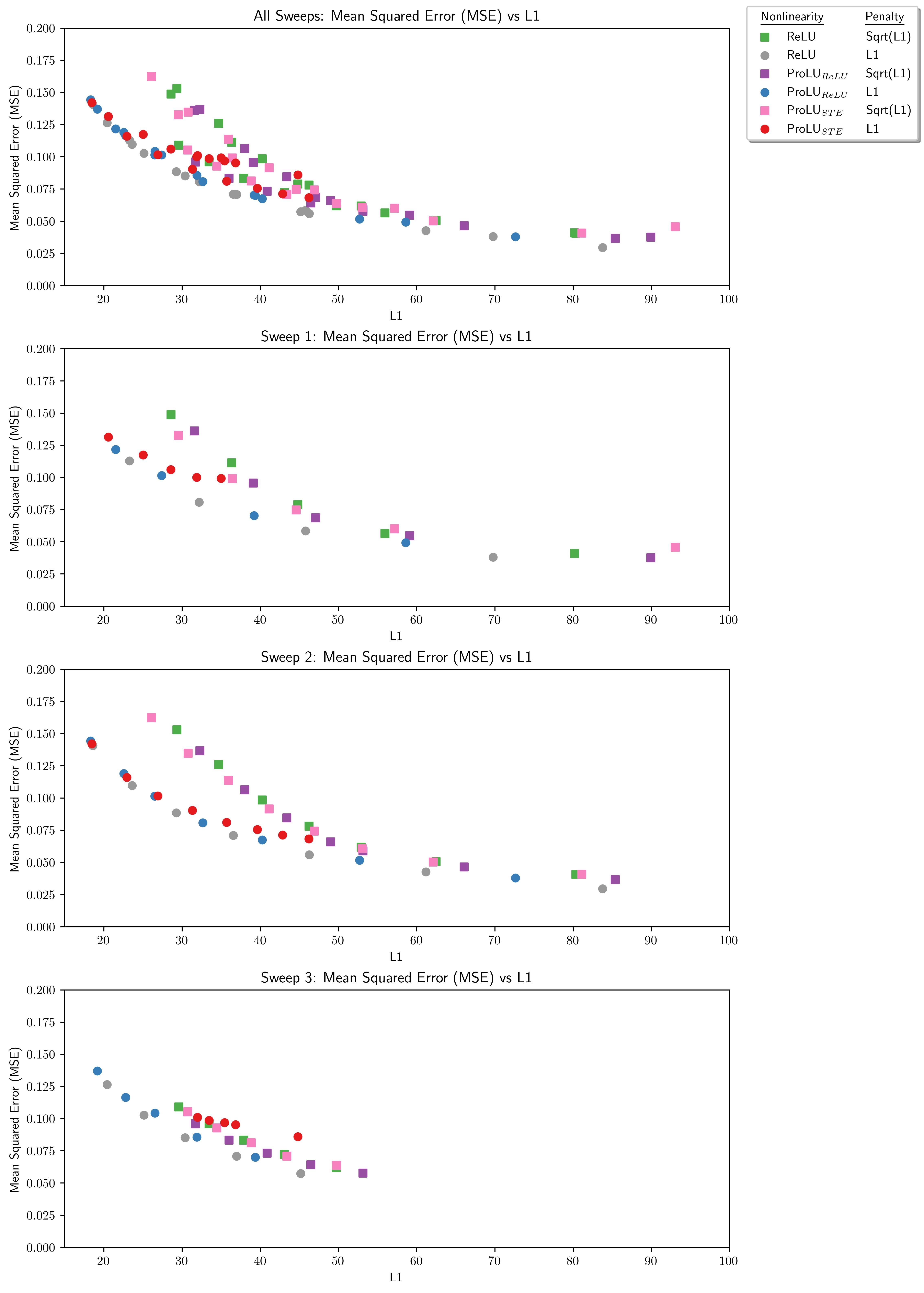 In favor of the hypothesis, while other architectures sometimes join it on the frontier, the Vanilla ReLU is present for the entirety of this Pareto frontier. On the other hand, at lower sparsity levels ProLUSTE joins it at the frontier. So the part where this change does not improve performance on the optimization target seems true, but it's not clear that better performance on the actual target is coming from worse performance on the optimization target.
In favor of the hypothesis, while other architectures sometimes join it on the frontier, the Vanilla ReLU is present for the entirety of this Pareto frontier. On the other hand, at lower sparsity levels ProLUSTE joins it at the frontier. So the part where this change does not improve performance on the optimization target seems true, but it's not clear that better performance on the actual target is coming from worse performance on the optimization target.
This suggests a possible reason for why the technique works well:
Possibly the gains from this technique do not come from scale consistency so much as that it forced us to synthesize some gradients and those gradients happened to point more in the direction of what we actually want.
Here is the graph of L1 norm versus L0 norm:
This looks like it's possible that what is working well here is the learned features are experiencing less suppression, but that may not be the only thing going on fixing this. Feature suppression is still consistent with the scale consistency hypothesis, as consistent undershooting would be an expected side effect if that is a real problem, since regular SAEs may be less able to filter unwanted activations if they are keeping biases near zero in order to minimize errors induced by scale inconsistency.
More investigation is needed here to create a complete or confident picture of what is cause of the performance gains in ProLU SAEs.
Unfortunately, I did not log √L1 so I can't compare with that curve, but could load the models to create those graphs in follow-up work.
Acknowledgements
Noa Nabeshima and Arunim Agarwal gave useful feedback and editing help on the draft of this post.
Mason Krug for in depth editing of my grant proposal, which helped seed this writeup and clarify my communication.
How to Cite