Our write up largely agrees with @Quintin Pope's summary, with the addition of training trajectory visualizations and an explanation of the MLP construction that solves modular addition.
A meta note that didn't make it into the article — with so many people looking into this problem over the last 18 months, I'm surprised this construction took so long to find. The modular addition task with a 1-layer MLP is about as simple as you can get![1]
Scaling mechanistic interpretability up to more complex tasks/models seems worth continuing to try, but I'm less sure extracting crisp explanations will be possible.[2] Even if we "solve" superposition, figuring the construction here — where there's no superposition in the generalizing model — wasn't trivial.
gif/twitter summary
If we train a MLP to solve modular addition, the generalizing phase has suggestive periodic patterns.
To figure out why the model generalizes, we first look at task where we know the generalizing solution — sparse parity. You can see the model generalizing as weight decay prunes spurious connections.
One point from the Omnigrok paper I hadn't internalized before training lots of models: grokking only happens when hyper-parameters are just right.
We can make other weird things happen too, like AdamW oscillating between low train loss and low weights.
To understand how a MLP solves modular addition, we train a much smaller model with a circular input embedding baked in.
Following @Neel Nanda and applying a discrete Fourier transform, we see larger models trained from scratch use the same star trick!
Finally, we show what the stars are doing and prove that they work:
Our ReLU activation has a small error, but it's close enough to the exact solution — an x² activation suggested in Grokking modular arithmetic — for the model to patch everything up w/ constructive interference.
And there are still open question: why are the frequencies with >5 neurons lopsided? Why does factoring Winput not do that same thing as factoring Woutput?
Our write up largely agrees with @Quintin Pope's summary, with the addition of training trajectory visualizations and an explanation of the MLP construction that solves modular addition.
A meta note that didn't make it into the article — with so many people looking into this problem over the last 18 months, I'm surprised this construction took so long to find. The modular addition task with a 1-layer MLP is about as simple as you can get![1]
Scaling mechanistic interpretability up to more complex tasks/models seems worth continuing to try, but I'm less sure extracting crisp explanations will be possible.[2] Even if we "solve" superposition, figuring the construction here — where there's no superposition in the generalizing model — wasn't trivial.
gif/twitter summary
If we train a MLP to solve modular addition, the generalizing phase has suggestive periodic patterns.
To figure out why the model generalizes, we first look at task where we know the generalizing solution — sparse parity. You can see the model generalizing as weight decay prunes spurious connections.
One point from the Omnigrok paper I hadn't internalized before training lots of models: grokking only happens when hyper-parameters are just right.
We can make other weird things happen too, like AdamW oscillating between low train loss and low weights.
To understand how a MLP solves modular addition, we train a much smaller model with a circular input embedding baked in.
Following @Neel Nanda and applying a discrete Fourier transform, we see larger models trained from scratch use the same star trick!
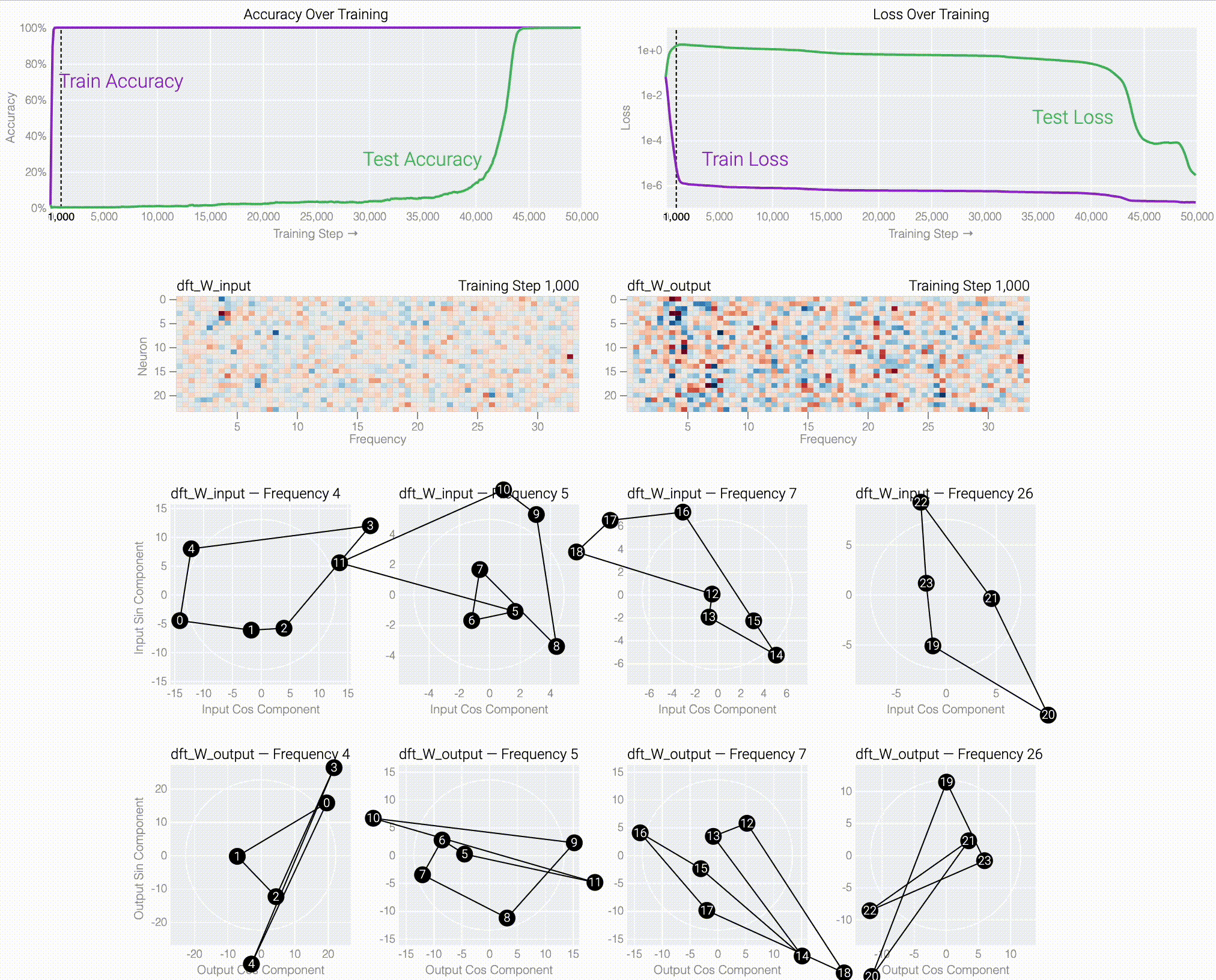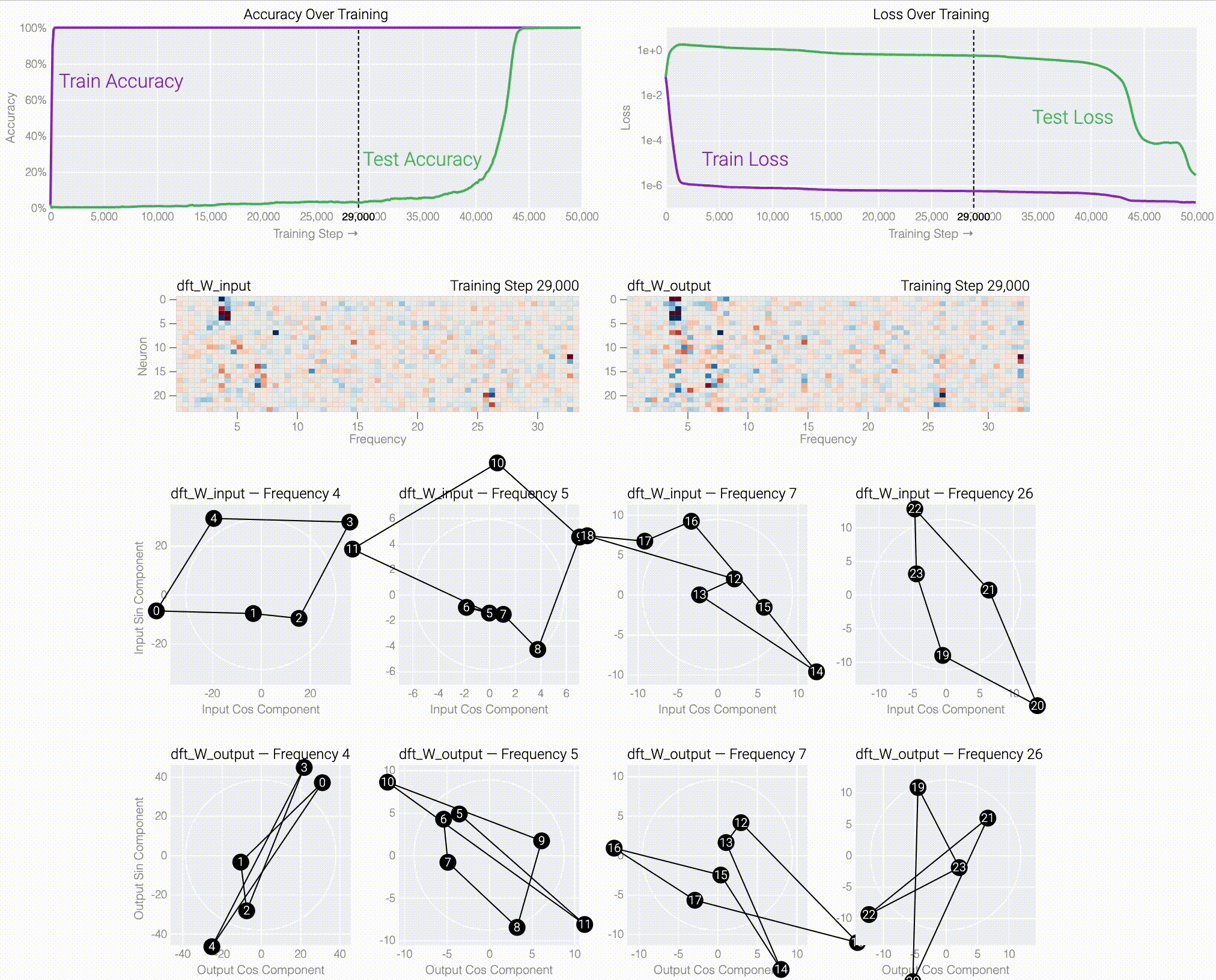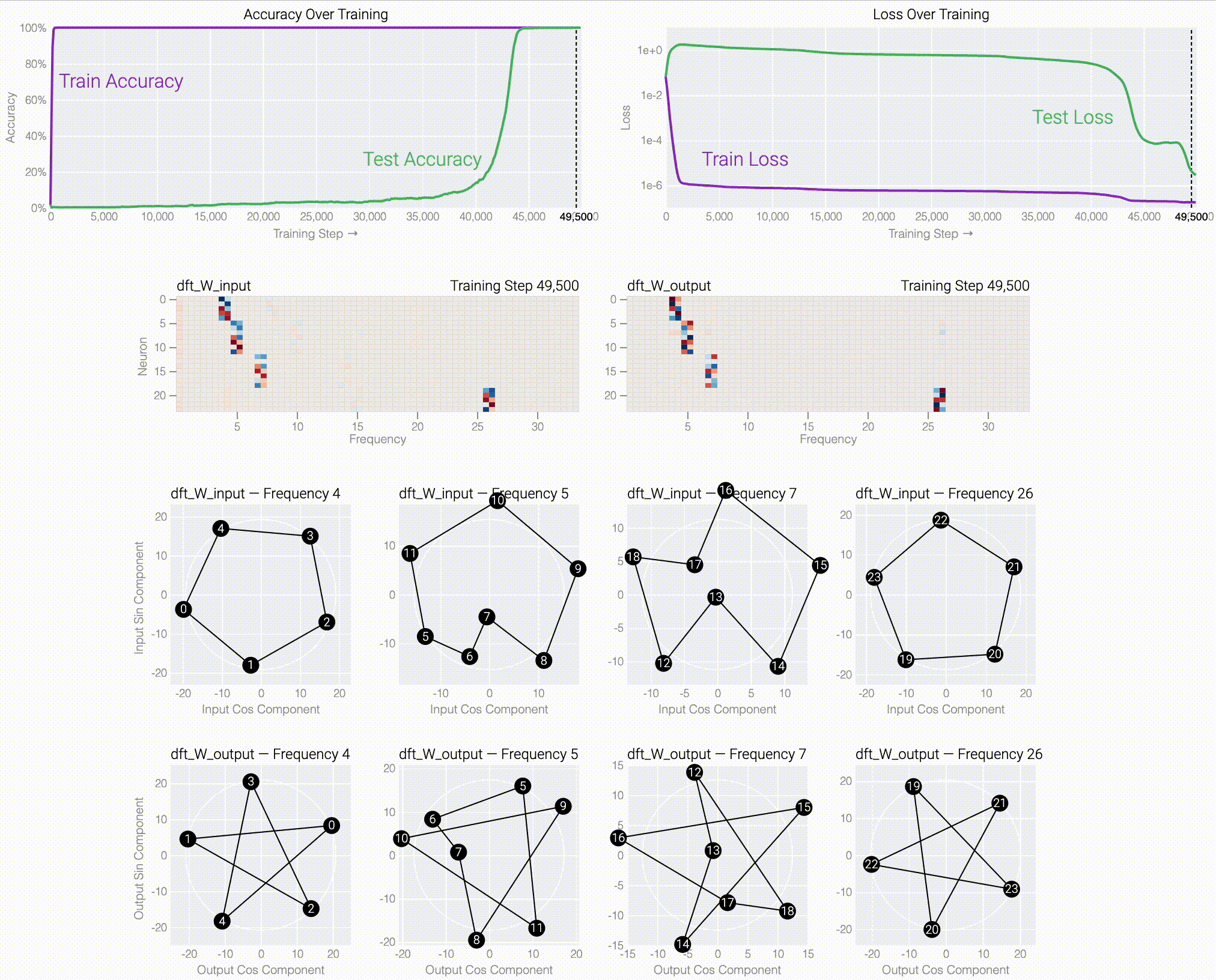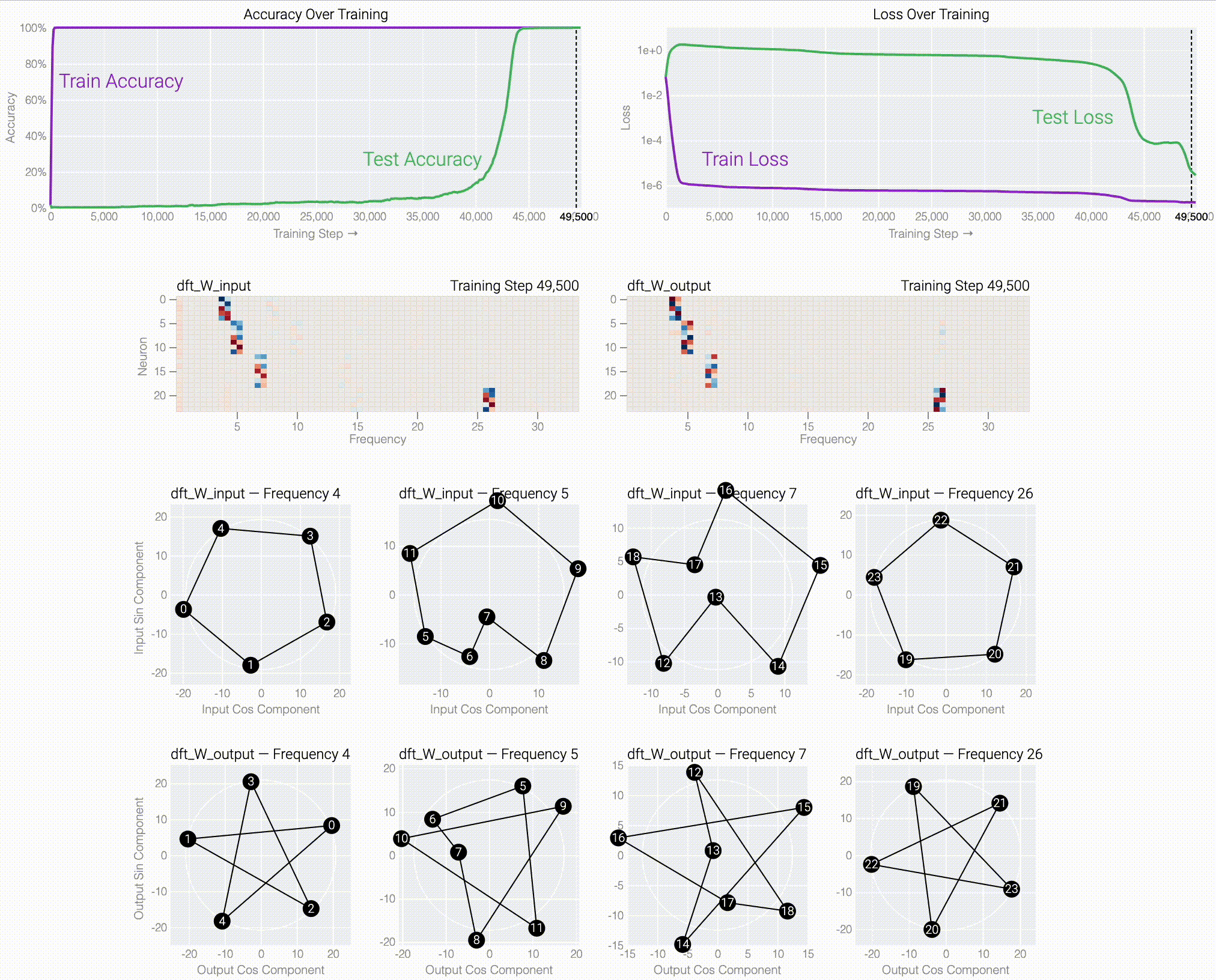
Finally, we show what the stars are doing and prove that they work:
Our ReLU activation has a small error, but it's close enough to the exact solution — an x² activation suggested in Grokking modular arithmetic — for the model to patch everything up w/ constructive interference.
And there are still open question: why are the frequencies with >5 neurons lopsided? Why does factoring Winput not do that same thing as factoring Woutput?
Also see The Hydra Effect: Emergent Self-repair in Language Model Computations