The following discussion was inspired by a comment on Vanessa Kosoy's Shortform regarding affine infradistributions. I expect the results here would not be considered surprising or novel by an expert in quantum logic or lattice theory. In particular [HTZ16^[1]] shows the unsolvability of the problem described below, and [HZ10^[2]] covers many related results as well. However, I haven't found this exact result written down anywhere, and I expect this beginner-friendly and mostly self-contained exposition to be useful for a reader interested in a glance into quantum logic.

Setup

The term "quantum logic" is often used to refer to the structure formed by subspaces of a Hilbert space (thought of as quantum propositions). The analogs of logical 'and', 'or', and 'not' are taken to be the operations of intersection, sum, and complements of subspaces, respectively. We can loosen this structure by dropping the inner product (so downgrading our Hilbert space to just a vector space), and hence the notion of orthogonal complements. We can call the resulting simplified logic "non-unitary" (for the lack of an inner product) quantum logic. We'll restrict our attention to the finite dimensional case. The following is the corresponding syntax and semantics.

Syntax

Let be a set of propositional variables. We define the set $L$ of well-formed formulas recursively as follows.

Two special symbols $⊤, ⊥ \in L$ ,
For any $p \in P$ , we have $p \in L$ ,
For any $ϕ, ψ \in L$ , we have $ϕ \land ψ \in L$ , and $ϕ \lor ψ \in L$ .

A theory $T$ is a subset $T \subset L \times L$ . Elements of $T$ are written $ϕ ⊢ ψ$ . We'll write $ϕ = ψ$ for when both $ϕ ⊢ ψ$ and $ψ ⊢ ϕ$ .

Semantics

For a vector space $V$ , let $Sp (V)$ denote the set of all linear subspaces of $V$ .

Definition 1. A model consists of a finite dimensional vector space $V$ , and a map $M : L \to Sp (V)$ , satisfying the following:

$M (⊥) = 0$ (the subspace consisting of the zero vector)
$M (⊤) = V$
$M (ϕ \lor ψ) = M (ψ) + M (ϕ)$
$M (ϕ \land ψ) = M (ψ) \cap M (ϕ)$ .

We say $M$ models the theory $T$ , if $M (ϕ) \subset M (ψ)$ for every $ϕ ⊢ ψ$ in $T$ .

Lattices

The set $Sp (V)$ forms a lattice under ' $\cap$ ' and ' $+$ ', with partial order given by ' $\subset$ '. Thus the map $M$ defining the model factors through the lattice quotient of the language $L$ (this is the free bounded lattice generated by the propositional variables, which we'll also call $L$ by abuse of notation).

Given a theory $T$ , we can take the quotient of the lattice $L$ by the relations specified in $T .$ More precisely we quotient by the congruence relation $θ$ generated by $T$ as follows. We can replace each $ϕ ⊢ ψ$ by $ϕ \land ψ = ϕ$ , so we can assume $T$ only contains equalities. Then we define the congruence relation $θ$ as the smallest congruence relation for which $ϕ \sim_{θ} ψ$ whenever $ϕ = ψ$ is in $T$ . Taking the quotient by this congruence relation we end up with a lattice corresponding to $T$ , which we'll denote $L (T) = L / θ$ . If $M$ models $T$ , then $M$ factors as a lattice homomorphism $L (T) \to Sp (V) .$

Example

For example, if $T$ consists of $a \land b = ⊥$ , and $a \lor b ⊢ c$ , we end up with the following lattice $L (T)$ :

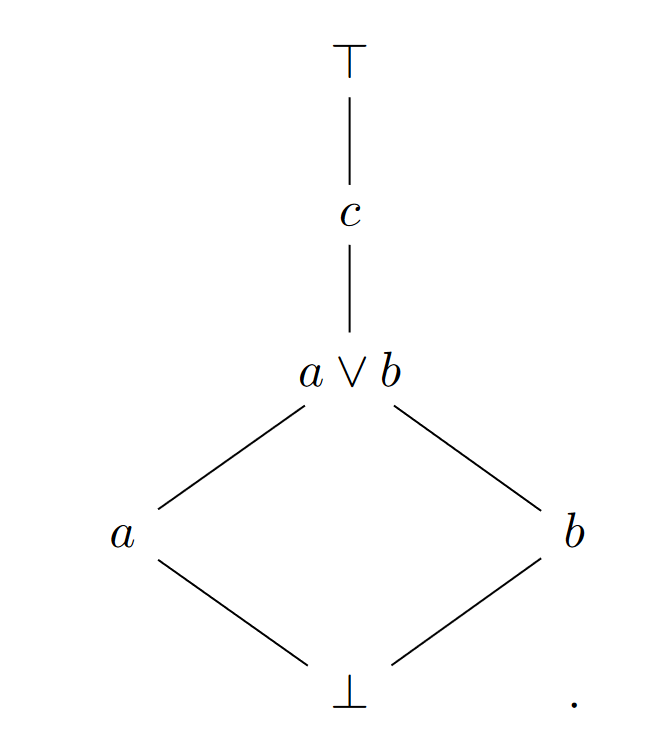
Classical vs Quantum Logic

In classical (Boolean) logic, a model would be a lattice homomorphism from $L$ to $P (X)$ , the lattice of subsets of a set $X$ , while in quantum logic we use the lattice of subspaces of a vector space. The key characteristic of classical logic is the distributive property:

ϕ \land (ψ \lor χ) = (ϕ \land ψ) \lor (ϕ \land χ),

and its dual.

Note that any classical model of a theory also gives rise to a quantum model by taking the vector space $V$ with basis the set $X$ , and composing with the lattice homomorphism $P (X) \to Sp (V)$ given by span.

Example: the double slit experiment

It's educational to consider an example of a non-classical quantum logic. Consider 3 events $A$ , $B$ , and $C$ (can be thought of as a particle passing through the first slit, passing through the second slit, and hitting the screen at a given point, respectively), whose corresponding propositions form the following non-distributive lattice (called $M_{3}$ ):

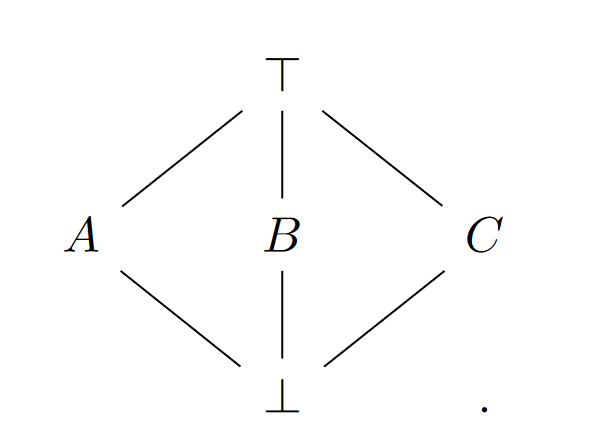
It is easy to see that $M_{3}$ cannot be represented as a lattice of subsets due to the failure of distributivity. However, we can model $M_{3}$ as three distinct lines in the lattice of subspaces of the plane.

Consistency in Quantum Logic

We call a theory $T$ consistent if it has a non-trivial (i.e. where $M (⊤) \neq M (⊥)$ ) model. Boolean consistency (or satisfiability) is well-know to be NP-hard, so it's natural to ask about the complexity of deciding consistency in the quantum setting.

One immediate necessary criterion for consistency can be seen as follows. If $M : L (T) \to Sp (V)$ is a lattice homomorphism, then by taking the dimension of subspaces, we get a map $d = dim (M) : L (T) \to N$ satisfying the following properties:

$d (⊥) = 0$ , and $d (⊤) = dim (V) > 0$
$d (a) \leq d (b)$ whenever $a \leq b$
$d (a) + d (b) = d (a \lor b) + d (a \land b)$ .

We might wonder whether the existence of such a $d$ is sufficient.

Conjecture 2. Given a dimension function $d$ as above, there exists a linear representation of $L (T)$ with dimensions as specified by $d$ .

If this conjecture were true, that would mean the existence of a polynomial time algorithm to check quantum satisfiability (since finding such a $d$ is a linear programming problem). As it turns out, the conjecture is false, which we show in Counterexample 2. Hence the proposed simple polynomial time algorithm to check quantum consistency doesn't work. Indeed, quantum consistency turns out to be unsolvable^[1].

Lattice Theory Prerequisites

Modular lattices

Vector subspaces have the property that if $U \subset V$ and $dim (U) = dim (V)$ then $U = V$ . So any linear representation of the lattice $L (T)$ would factor through the quotient lattice where if $a \leq b$ and $d (a) = d (b)$ we identify $a$ and $b$ . The resulting quotient lattice $¯ ¯¯¯¯¯¯¯¯¯¯¯ ¯ L (T)$ and the induced map $¯ d$ would satisfy a stronger version of the properties 1-3 above, where in 2 we now have $d (a) < d (b)$ whenever $a < b$ . It turns out that lattices with such a function $¯ d$ are exactly the modular lattices (with the additional property of every bounded chain being finite). These results are spelled out in point 7 and Theorem 9 of Chapter V in [Bir40^[3]].

Thus Conjecture 2 boils down to whether these modular lattices always have non-trivial linear representations. This seems somewhat unlikely at first glance, since linear subspace lattices need to satisfy additional properties, e.g. the arguesian property (discussed further in the "Arguesian lattices" section), and indeed in Counterexample 9 we show that this is not the case.

Definition 3. For $a, b \in L$ in a lattice, the quotient (also called the interval) $[a / b]$ is the sublattice

[a / b] = {x \in L | b \leq x \leq a}

Definition 4. For any $x, y \in L$ in a lattice we say the quotients $[x \lor y / y]$ and $[x / x \land y]$ are projective (to each other). So being projective is the equivalence relation generated by these pairs of quotients.

Definition 5. A quotient $[a / b]$ is called prime if $b < a$ , but there's no $x$ such that $b < x < a$ .

Lemma 6. A modular lattice of finite length is simple (i.e., without proper congruence relations) if and only if all its prime quotients are projective (to each other). Note that being simple means having no proper non-trivial quotients.

Proof. This is Corollary 1 in Chapter V, Section 7 of [Bir40^[3]]. We only need the simpler "if" direction here, which is fairly straightforward to see directly as follows. If $θ$ is a congruence relation on $L$ , then $x \sim_{θ} x \lor y$ implies $x \land y \sim_{θ} (x \lor y) \land y = y$ , and the dual claim also holds. So if a certain quotient is annulled by $θ$ (i.e. made equivalent) then so is every projective quotient.

Now assume $θ$ is non-trivial, so $x \sim_{θ} y$ for some $x \neq y$ . Then also $x \lor y \sim_{θ} y \sim_{θ} x \land y$ . Since $L$ is finite length, there is some $x \land y \leq ~ x \leq x \lor y$ with $[x \lor y / ~ x]$ prime (and $x \lor y \sim_{θ} ~ x$ ). Then by the above every prime quotient is annulled by $θ$ , which in a finite length lattice implies that $θ$ annuls everything. ◻

Arguesian lattices

Definition 7. A modular lattice $L$ is called arguesian if for any $a_{i}, b_{i} \in L$ ( $i = 0, 1, 2$ ),

(a_{0} \lor b_{0}) \land (a_{1} \lor b_{1}) \leq a_{2} \lor b_{2}

implies

c_{2} \leq c_{1} \lor c_{2},

where $c_{i} = (a_{j} \lor a_{k}) \land (b_{j} \lor b_{k})$ ( ${i, j, k} = {0, 1, 2}$ ).

This is the lattice-theoretic formulation of Desargues' theorem, considering the incidence lattice of a projective space:

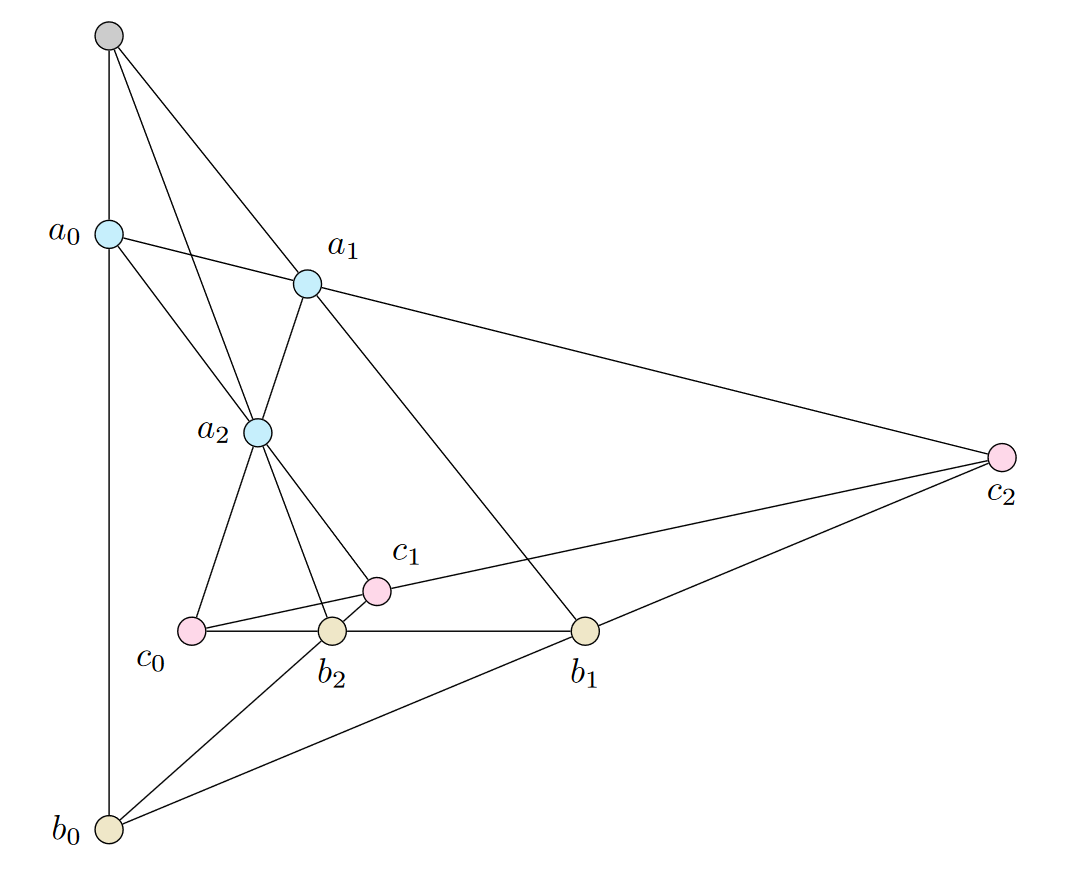
Lemma 8. For any ring $R$ , the lattice of submodules $L (M)$ of a (left) $R$ -module $M$ is an arguesian lattice. In particular any sublattice of $L (M)$ is also arguesian.

Proof. Let $A_{i}$ , $B_{i}$ be submodules such that the assumption in the arguesian property

\begin{matrix} (A_{0} + B_{0}) \cap (A_{1} + B_{1}) \subset A_{2} + B_{2} \\ (1) \end{matrix}

is satisfied. Let $C_{i} = (A_{j} + A_{k}) \cap (B_{j} + B_{k})$ . We want to show that $C_{2} \subset C_{0} + C_{1}$ . Let $γ_{2} \in C_{2}$ , so by definition

γ_{2} = α_{0} + α_{1} = β_{0} + β_{1}

for $α_{i} \in A_{i}$ , and $β_{i} \in B_{i}$ . Now

x := α_{0} - β_{0} = β_{1} - α_{1} \in (A_{0} + B_{0}) \cap (A_{1} + B_{1}),

so by (1) we have $x \in A_{2} + B_{2}$ , i.e. $x = α_{2} + β_{2}$ for $α_{2} \in A_{2}$ and $β_{2} \in B_{2}$ . But then

γ_{0} := α_{1} + α_{2} = β_{1} - β_{2} \in C_{0}

and

γ_{1} := α_{0} - α_{2} = β_{0} + β_{2} \in C_{1},

γ_{2} = γ_{0} + γ_{1} \in C_{0} + C_{1}

as required. ◻

A Counterexample

Counterexample 9. Conjecture 2 fails for the incidence lattice $L$ of a finite non-Desarguesian projective plane. Note that the smallest such plane has $91$ points, which corresponds to a theory $T$ on $91$ propositional variables.

Proof. The lattice $L$ is modular (an explicit dimension function $d$ can be defined by $d (p o i n t) = 1$ , and $d (l i n e) = 2$ for all points and lines). Being the incidence lattice of a non-Desarguesian plane, $L$ is not arguesian. This lattice also turns out to be simple (i.e. without any smaller non-trivial quotients), and so by Lemma 8 it cannot have a non-trivial linear representation. The fact that $L$ is simple follows from Lemma 6 after showing that all prime quotients are projective for this incidence lattice.

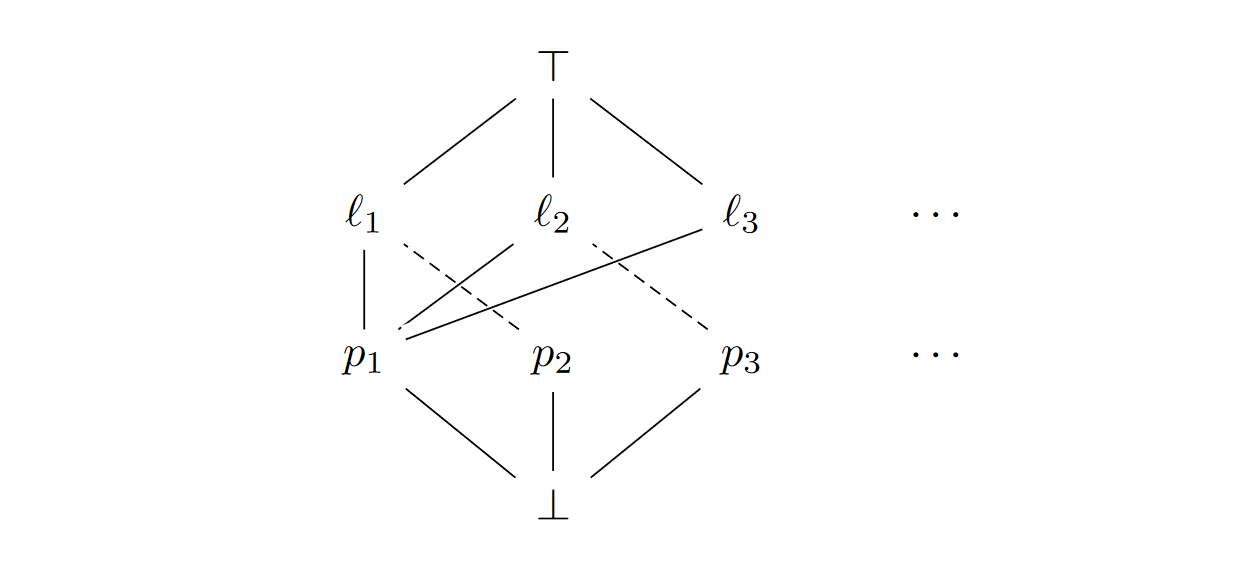
First consider a point $p$ in the projective plane, and let $ℓ_{1}, ℓ_{2}, ℓ_{3}, \dots$ be the distinct lines through $p$ . Then by definition (using $\sim_{p}$ here to denote intervals projective to each other) $[⊤ / ℓ_{i}] \sim_{p} [ℓ_{j} / p]$ , and $[⊤ / ℓ_{j}] \sim_{p} [ℓ_{i} / p]$ for any $i \neq j$ . Since there are at least three lines through $p$ , this then implies all of $[⊤ / ℓ_{i}]$ , and $[ℓ_{i} / p]$ are projective to each other for all $i$ by transitivity.

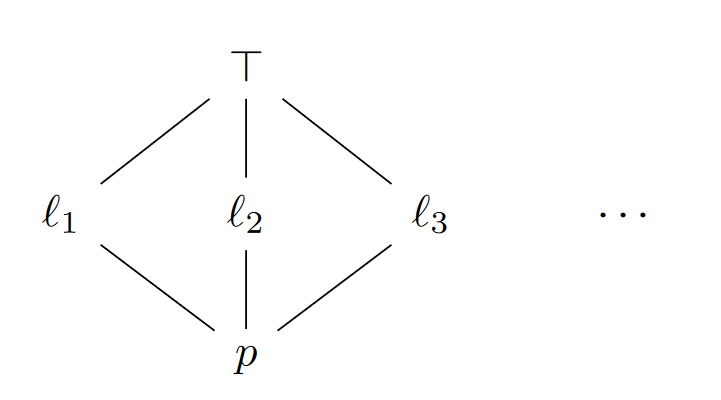
Now let $q$ be a point distinct from $p$ , and let $ℓ$ be the line through $p$ and $q$ . Then from the above $[⊤ / ℓ]$ is projective to both $[ℓ / p]$ and $[ℓ / q]$ , which in turn are projective to $[p / ⊥]$ and $[q / ⊥]$ .

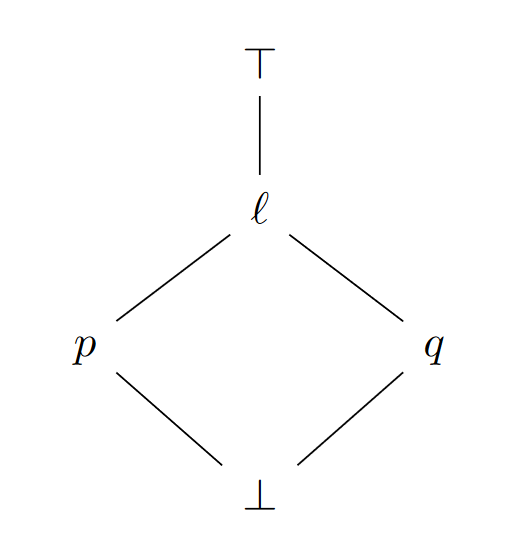
Putting all of these together, since any line contains at least one point, we can deduce that in fact all prime quotients are projective to each other in the incidence lattice. ◻

To construct a theory $T$ from Counterexample 9, we can introduce propositional variables $P_{i}$ corresponding to the points $p_{i}$ of the projective plane, $L_{i}$ corresponding to the lines $ℓ_{i}$ , and let $T$ contain all the following:

$P_{i} \land P_{j} = ⊥$ for $i \neq j$
$L_{i} \lor L_{j} = ⊤$ for $i \neq j$
$P_{i} ⊢ L_{j}$ if the point $p_{i}$ lies on the line $ℓ_{j}$
$P_{i} \lor P_{j} = L_{k}$ if $ℓ_{k}$ is the line through $p_{i}$ and $p_{j}$ for $i \neq j$
$L_{i} \land L_{j} = P_{k}$ if $p_{k}$ is the point of intersection of $ℓ_{i}$ and $ℓ_{j}$ for $i \neq j$ .

^{^}
Christian Herrmann and Yasuyuki Tsukamoto and Martin Ziegler. On the consistency problem for modular lattices and related structures, 2016
^{^}
Christian Herrmann and Martin Ziegler. Computational Complexity of Quantum Satisfiability, 2010
^{^}
[Bir40] Garrett Birkhoff. Lattice Theory. American Mathematical Society, New
York, 1940

AI ALIGNMENT FORUM
AF