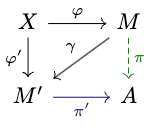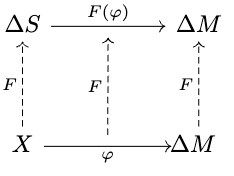The natural abstraction hypothesis claims (in part) that a wide variety of agents will learn to use the same abstractions and concepts to reason about the world.
What's the simplest possible setting where we can state something like this formally? Under what conditions is it true?
One necessary condition to say that agents use 'the same abstractions' is that their decisions depend on the same coarse-grained information about the environment. Motivated by this, we consider a setting where an agent needs to decide which information to pass though an information bottleneck, and ask: when do different utility functions prefer to preserve the same information?
As we develop this setting, we:
- unify and extend the Blackwell Informativeness and Good(er) Regulator theorems
- investigate the minimum structure needed for strong natural abstractions (in this sense) to exist
- give examples where strong natural abstractions a) exist b) don't exist c) exist at some levels of capability, but not at others - including cases where the natural abstractions at different sizes are orthogonal
- demonstrate that (very) weak natural abstractions exist under weak conditions
- formally connect natural abstractions to instrumental power-seeking incentives, and characterize them in a way inspired by Turner's power-seeking theorems.
(As far as I can tell, apart from the obvious cited Theorems, these results are original[1])
Whereas Wentworth's abstraction work has focused on what natural abstractions might look like, and why we might expect them to exist, this work focuses on exploring what it would mean for something to be a natural abstraction in the first place. Rather than an attempt to answer the natural abstraction hypothesis, it is more an attempt to understand the question.
1. Base setting
Any agent exists within an environment that is bigger than itself. It therefore necessarily maps a large number of potential environment states to a smaller number of internal states. When it then chooses what action to take, this choice depends only on its internal state.
Roughly, we can consider this mapping from the environment to action-influencing internal states to be the agent's abstractions[2]. We want to understand when different utility functions will share preferences about how to do this mapping - under the natural abstraction hypothesis, in appropriate conditions, there should be certain abstractions that are convergent across most utility functions.
To model this, we'll consider a game where:
- There is some initial context
- An agent writes a message, conditional on this context
- The agent takes an action, conditional on the message
- The agent gets some utility that depends on the context and its action.
We'll keep everything finite to start - any infinities we want we should come by honestly, by taking limits. Our one concession to this is that we'll allow normal real-valued probabilities and utilities (though we'll see eventually how we could do without if we felt like it).
Formally, define:
: a set of context states
: a set of signals
: a set of actions
: , a utility function
: , an encoder mapping states to a distribution of signals
: , a policy mapping signals to a distribution over actions
We allow and to be stochastic (stochastic maps), but we'll also pay special attention to the case where they are deterministic (so effectively , ), because it is especially clean and factors apart some of the dynamics we're interested in.
Now, we are interested in preferences over assuming that is chosen optimally. When are these preferences, and the optimal encoders, the same for different ? What happens as we vary ? For the time being, we can equally consider different to be different agents or different tasks faced by the same agent. Later, we'll see some places where the two interpretations diverge.
As one might expect of such a simple setup, similar formalisms have been considered in many other contexts. Most directly, exactly this game is studied in the decision theory and economics literature - with partial overlap with our questions. There, the objects are commonly referred to as 'information structures' or 'Blackwell experiments'; we'll use the former term.
One other remark on notation: we'll often be interested in comparing different encoders , which may have different signal spaces . We'll write for , the cardinality of the signal set.
1.1 Equivalence classes of encoders
One thing to note out of the gate: 'the same encoder' here shouldn't mean equality as functions. For our current purposes, we care only about their information content - so if are the same except for a relabelling of , we want to consider them identical (and they will certainly have the same attainable utility for any ). Another way to say this: we want to quotient by , i.e. the permutations of , to get our real objects of interest. What are these objects?
In the deterministic case, they are the distinct possible sets of preimages - which are just the -part partitions of . In the general case, they are a more general partition-like object. Note that we can represent a stochastic map as an column-stochastic matrix: a matrix with elements in such that the sum of each column is : . Then gives the probability that we encode signal given we are in state - that is, . If we are indifferent to permutations of , then we are indifferent to permutations of the rows, so we have a set (rather than vector) of row vectors. (If were instead a suitable topological space and continuous, then these would be exactly partitions of unity)
Sometimes it will be more convenient to think of as a function, sometimes to think of it as a partition , and sometimes as a matrix; we'll switch between all three as appropriate. However, keep in mind we really only care about up to equivalence in this sense.
1.2 Comparison of encoders
For a given utility function , we take the value of an information structure to be the expected utility if we have that information structure and follow the optimal policy.
Formally, define ; we can also say it is , extending to a function on distributions by taking the expectation. (By convention we're assuming a uniform prior on ; this choice turns out to be irrelevant for our purposes).
We say that prefers to if , which we'll also write .
2. Basic properties for individual
As a first step, to get a feel for the setting, let's start with some observations about what can happen for arbitrary individual . These give us one bound on common properties - for something happen for 'many' , it must certainly happen for some particular .
2.0 should be a bottleneck
One basic observation is that the problem becomes trivial if or . At that point, we can always pick the globally optimal action for each value of . For this setting to be remotely interesting, needs to be an information bottleneck.
2.1a Any deterministic partition is optimal for some
This is also easy to see: for a partition , take any and define . Furthermore, any optimal partition for this must be a refinement of , and is the unique optimal partition with parts.
2.1b For any , any nondeterministic is weakly dominated by some deterministic
It is not quite literally the case that no nondeterministic is optimal for its size for any . If is indifferent between where to put in the optimal policy, say , then can be freely sent to any mixture of and . But there is always a deterministic of less than or equal size which does at least as well, and either does strictly better or is strictly smaller unless is indifferent between some outcomes (which may have measure zero, depending on your assumptions).
Proof: See footnote[3]; nothing surprising.
This motivates considering only partitions in the context of optimality for a single (the remainder of section 2.)
2.2 Optimal partitions can be orthogonal
Fixing , write for the optimal partition of size . Then, there's not necessarily any relationship between and for .
For instance, take , and Then the optimal partition of size 3 is , while the optimal partition of size 4 is (easy exercise: show this). These partitions are orthogonal - in other words, they have zero mutual information. This example can be extended to make any finite number of optimal orthogonal.
2.3 Not every is (uniquely) optimal for any
Then, can any sequence of partitions whatsoever be optimal for the right ? Not uniquely so, at least (again ruling out e.g. the trivial case where U is constant and all partitions are optimal). Consider the following counterexample:
For to be uniquely optimal, it must be that subdividing red provides more marginal benefit than subdividing green or blue, but optimality of implies the opposite.
The general principle here: if two strictly size-optimal partitions both involve partitioning the same subset of into pieces, then they must do so the same way.
2.4 Strict monotonicity of
What about how the attainable utility varies with ? Write for the maximum expected utility attainable when , and for the global maximum . Obviously for , we have ; and in fact, if , then .
An easy way to see this is to consider - the number of distinct optimal actions. Then if , we can always improve by using the additional partition to move some from a suboptimal action to an optimal action. If then we can assign every it's optimal action and .
Naively, you might imagine there could be a scenario where more information doesn't help until you reach some threshold. For instance, suppose you can either a) do nothing or b) enter a 5-bit password to attempt to open a safe; the safe explodes if you fail, so it's only worth attempting if you definitely know the full password. However, even though you need to know the whole password to change your policy, you can convey the whole password a smaller fraction of the time. Even with only two states for , you can have one state represent 'password unknown, do nothing', and the second (rare) state represent 'the password is exactly 00000, so enter that'. This result shows that to get that kind of thresholding behavior, we'd need to add something else to the model, i.e. that constrains the allowed partitions.
2.5 Marginal return can increase
We might expect that you use your first split to encode the most important information, the next split to encode the next most important information, etc., so that the marginal return to channel capacity is always decreasing. It turns out this is not necessarily the case. Consider the following counterexample:
, and With a single part, the best we can do is everywhere, so ; with three parts, we can divide along the environment's second dimension and get 21 everywhere, so the average is . But we've chosen the utilities so the best we can do with two parts is to divide along the first dimension, achieving 8 average utility: any policy for a 2-part partition which uses a action must either suffer -1000 for some , or divide between and a single part on at most 1/3 of , achieving at most 21/3 = 7 utility. So , and .
3. Dominance over all
Now that we've gotten a taste of the constraints that exist for individual and , let's move to our main topic: common preferences among multiple . Start from the opposite extreme: what preferences over information structures are shared by all possible utility functions?
This turns out to be exactly the question answered by the foundational result about information structures: the Blackwell Informativeness Theorem.
Unsurprisingly, given the strength of the requirement and lack of structure in our setting, these convergent preferences will be sparse. The result is not exactly a no-free-lunch theorem, since some information structures are indeed better than others, but it's not so far off in spirit: we can think of it stating that only the minimum possible preferences are shared.
Based on the barriers this case reveals, we'll then extend our setting so that non-trivial convergence is possible.
3.1 The Blackwell order
What is required for to be preferred to for all ? One clear sufficient condition is that given , we can use it to build by postprocessing - then we can imitate any policy for . And we might expect that this is also necessary: if not, must not distinguish some situations which distinguishes, and we can construct some that cares about the difference.
This is what the Blackwell Informativeness Theorem confirms; and once we cast it in just the right terms, the proof falls out almost immediately.
Since some of our later results have very similar proofs, we'll reproduce the argument here. We follow the presentation of the paper "Blackwell’s Informativeness Theorem Using Diagrams" and especially of this twitter thread.
We'll need one additional definition:
Definition: Attainable outcomes
Define to be the attainable outcome distributions of .
That is, an element is a probability distribution over with for some . Note that we can equivalently consider to be the set of stochastic maps themselves, i.e. the likelihoods , up to isomorphism by application to our uniform prior on [4]. In other words, ; these can in turn be considered vectors in .
Then we can state the theorem:
Blackwell Informativeness Theorem
The following are equivalent:
- There exists some stochastic map such that . We also say this as: " is a garbling of ".
- for any
- For any and , we have .
When these hold, write .
Proof:
: If you is a garbling of , and you have , you can just do the garbling yourself to get ; so you can certainly act according to if you want to.
Let be a garbling of .
By definition, for any there is a s.t. . Then defining , the diagram commutes[5], showing .
: If can achieve whatever can, then in particular it can achieve "be ", which makes a garbling.
Take - then for , 2) says there is a such that the diagram commutes. Then is a garbling of .
: If contains , then it gives strictly more options, so your best option is at least as good - .
: This is the one step which isn't immediate from the definitions - it's instead an application of a separation theorem.
Suppose is false, say . Now and are convex and compact, so the hyperplane separation theorem states that we can find a such that for all and for - a hyperplane with normal vector separating them. But this is exactly a where does worse than , contradicting 3).
Notice that the equivalence classes of are exactly what we said are really 'the same' information structure: one way to see this is to note that and imply , and the only stochastic matrices with an inverse within the stochastic matrices are permutation matrices, which just interchange the states of . So the only way one information structure can be universally preferred to a second is if one 'contains' the other, and two information structures which all are indifferent between are 'the same one'.
When and are deterministic, we can easily show that this is equivalent to being refinement of as a partition (from property 1, or by explicitly constructing for property 3). For this case, we can then state the result as: the partial order of dominance of deterministic information structures is equal to their standard partial order as partitions.
We can also remark that this is a strictly stronger requirement than having more mutual information with than . While is a necessary condition for , it is not a sufficient one - must contain "a superset of" 's information about , rather than simply "more" information about .
Some corollaries for partitions:
- No partition of size dominates any other (non-degenerate) partition of size
- is always the unique smallest partition dominating itself
- The discrete partition uniquely dominates all other partitions (and is the unique smallest information structure which dominates all others in general).
3.2 What's missing
So we've seen that by default, there's no nontrivial superiority of information structures over all possible utility functions. What's missing to allow for more interesting convergence behavior? Two things:
- A way to break the symmetry between different information structures. There's nothing to break the symmetry between different or actions, and so (for example) only part-sizes to break the symmetry between different partitions. This fundamentally prevents strong convergence to exact information structures of a given size.
- A non-extremal aggregation over utility functions. Looking at superiority over all utility functions is equivalent to considering only the worst-case. It also allows only boolean, not scalar, comparisons: either is or isn't better than for all . Instead, looking at 'most' (and 'how many') utility functions will let us make finer distinctions between the usefulness of information structures.
The symmetry is the sharpest obstacle to stronger convergence, so we'll address 1) first.
4. Adding structure
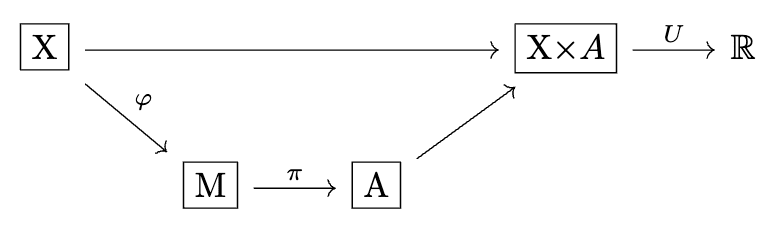
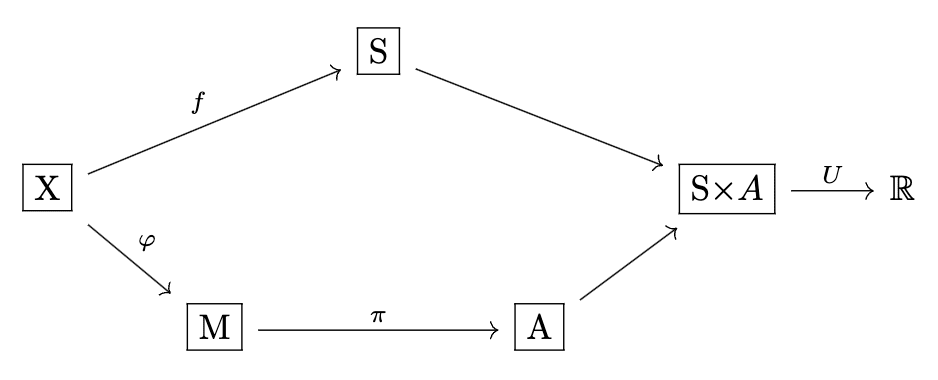
4.1 Adding a 'system': the Good(er) Regulator Theorem
As a first example of what happens when we introduce more structure - and because it leads us another existing theorem - let's ask: what if we restrict the distinctions between which the utility function is allowed to care about? What does this change about the preference dominance order?
The discrete version of this idea is for to treat some values of identically - at which point we can consider to be defined on the equivalence classes of , giving the 'causal' structure . What's the probabilistic version?
Well, we can simply take a stochastic map to the intermediate object, giving the structure , for some set and stochastic map (which we'll assume to be surjective[6] for convenience; otherwise reduce ). This is a kind of dimensionality reduction (as even if , certainly as a vector space).
Now our setting looks like this:
This may look familiar if you've read "Fixing The Good Regulator Theorem":
This is exactly the same setting, up to some choices of representation - the extra node just encodes the choice to look at a fixed encoder which must be shared[7] by many[8] policies and utility functions.
Taking the Good Regulator perspective, we can think of being the system we care about, with describing how its states depend on the observable . The question the Gooder Regulator Theorem asks is in fact just: given a system , what's the minimal information structure that dominates all others?
The Gooder Regulator theorem tells us that it should in some sense be the posterior distribution - we'll revisit this in a moment. (Meanwhile, in the discrete case: notice that , as an equivalence relation, can also just be viewed as partition of . We should expect that the optimal partition will just be .)
What about the full preference dominance order, like the Blackwell order gives us for the base setting?
4.1.1. The GR-Blackwell order
We can indeed give a characterization of this order which parallels the Blackwell Informativeness Theorem.
The key idea is to look at the new equivalence classes of with respect to : namely, the expected utility now depends exactly on what distribution of gets assigned each action . This suggests that we should look everything in terms of distributions over .
We then find that for to be dominated by , it's not necessary for to be a garbling of (though this is of course still sufficient), but only necessary that "the mapping of system states to signals implied by " is a garbling of "the mapping of system states to signals implied by ". They will further be equivalent if and only if they imply the same joint distribution of .
Formally,
GR setting definitions
Define by - the (stochastic) map induced by specifying 'how much do we map ( that result in) state to signal '.
Define the attainable -outcome distributions to be:
or isomorphically,
Just as the elements of correspond to stochastic maps formed by , the elements of correspond to stochastic maps formed by .
Then we have:
The GR-Blackwell order
The following are equivalent:
- There exists a stochastic map such that
- for any
- For any and , we have .
When they hold, write .
This is the same result as the Blackwell Informativeness Theorem, but after applying a functor which quotients out the equivalences induced by (while leaving everything else unchanged):
And once we've stated it like this, if we look at the proof of the regular Blackwell order, we can see that each part carries over almost exactly. Substitute and , and you've proved this new equivalence.
The only place an additional step is added is in (3)=>(2). Our separation theorem gives us (towards contradiction) a , such that for all .
Meanwhile, is ; but after some rearranging, this can be written , where .
This extra factor of is then no problem for the proof - we can just take (instead of ) as the contradictory utility function preferring . But it highlights how a) the likelihood of states doesn't impact preferences over all utility functions (though it can matter for other questions), and b) even if we start by considering only a uniform prior on , the introduction of the system allows us get back a weighted version of our setting. (Indeed, if we redefine 'information structures' to be equivalence classes of , this is exactly what we would have - but with some restrictions on the set of possible information structures if is nondeterministic).
Alternate precomposition form
In fact, another reflection of the same scaling invariance: while we normalized to be a proper stochastic map (i.e. column-stochastic matrix) by dividing by , the equation will hold iff the same equation holds[9] with unnormalized . Inspecting our equation for , we can observe that this unnormalized form of as a matrix is actually just . This gives us a nice alternate statement of prong 1), equivalent to all the rest:
1') There exists a stochastic matrix such that .
4.1.2 Gooder Regulator revisited
Let's explicitly show how the Gooder Regulator Theorem relates to the GR-Blackwell order, and the minimal information structure which weakly dominates all others.
Let - as a set, so potentially . And to make it clearer what role plays: we'll take to be an enumeration of it, rather than itself; write for the index of in .
Define by (deterministically).
Then the Gooder Regulator Theorem is to show that for all information structures :
- .
- If , then (i.e. additionally ).
We'll give a quick proof in these terms - not too different from Wentworth's, but taking advantage of the fact that allows for globally optimal actions.
Proof:
1) For the first part, we can just remark that for any , the globally optimal action for is [10], so the globally optimal behavior is achievable with a policy from . Hence dominates any possible information structure.
2) For the second part: if , by pigeonhole there necessarily exists an such that with .
It suffices to find a pair such that the optimal action for is different from the optimal action for - then will be lower than the global optimum, so and .
Hence we need vectors , such that
Taking , , we have the desired result.
Where's the posterior?
What here is isomorphic to "the posterior distribution on given ", , promised by the Gooder Regulator theorem?
It's certainly not the states of , in isolation - is just an arbitrary set with the right cardinality. It's more reasonable to say that it's (a.k.a. ). Indeed, and do induce the same equivalence classes of , so if we look at the posterior as a function (n.b. not as ), then they are isomorphic as functions.
However, this isn't necessarily the equivalence we're looking for. Different systems with different posteriors can induce the same optimal - as again, they just need to have the same equivalence classes of . That is, there's no isomorphism between and . Nor are systems yielding the same optimal necessarily 'effectively identical' - they can induce different overall preorders over information structures, with e.g. different (and even different numbers of) -optimal information structures. Contra Wentworth, the "model " (a.k.a ) by itself does not contain all of the information from the posterior.
That said, when we consider a single agent that can optimally satisfy any , it is still reasonable to say the agent as a whole must model the Bayesian posterior. This is because it must 'know' what distribution of states each signal corresponds to in order to choose the optimal policies for each (we can easily show this: the optimal policy for some would shift if were different). The distinction is just that this information doesn't have to be propagated from ; it doesn't have the type "something which must be a function of the observation". We can think of it as (allowed to be) precomputed, or built into the agent. Regardless, really it is the pair which must contain the full information from the posterior.
This is a bit of a subtle distinction, but the kind which can be important.
4.1.3 Convergence is still limited
Has this additional structure allowed for the possibility of natural abstractions, given the right system ? Generally, does this setting allow us to model the kind of preference structures over abstractions that we're interested in? Not entirely.
The reduction by does introduce additional convergence - and asymmetric convergence, as in general will differentially expand the equivalence classes and dominated sets of different information structures. But, especially in the 'universal preference' setting, we're still restricted by the identical role each must play in the outcomes.
One reflection of this is that for any short of the critical size allowing full information of the system, it is still impossible to make all utility functions agree on a single of size which they prefer to all others of that size. Surely we ought to at least be able to represent universal preferences for a particular compression.
While a full discussion of the number of Pareto optimal information structures at a given size is out of scope, we'll sketch a few quick properties:
- Just as in the Blackwell setting every partition of is the unique smallest partition dominating itself, when and are deterministic, every corresponding to a partition of is the unique smallest partition dominating itself.
- In general, the number (or volume) of -Pareto-optimal information structures scales at least[11] as , initially growing ~exponentially as diverges from or .
This limits the maximum possible convergence of abstractions. To go further, we must allow for more substantial shared structure between the utility functions.
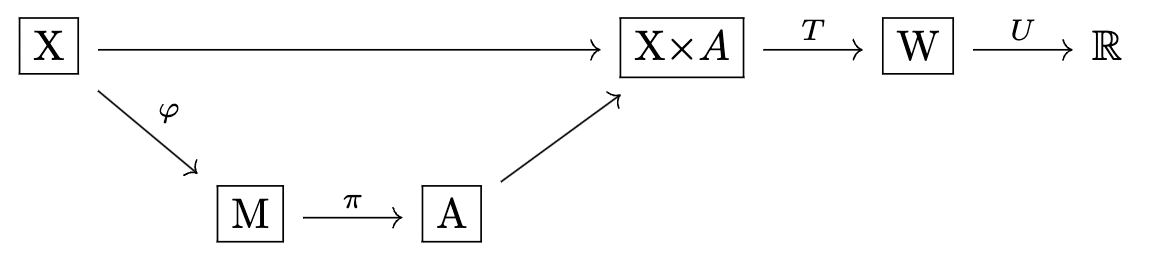
4.2. Adding a common world
Specifically, the additional structure we need is a common world, so that different utility functions share the same relationships between context states and actions.
Define:
: a set of outcomes
, a transition function
and redefine .
We'll call the pair a 'world'[12].
Our setting now looks like this:
Notice that if happens to factor as for some and , then we're back in the Gooder Regulator setting. Generally, for this additional structure to do anything new, must be many-to-one, and the images of different actions must overlap.
4.2.1 Universal preferences in a common world
In this setting, what can we say about universal preferences?
The equivalence of prongs (2) and (3) from the Blackwell Informativeness Theorem carries over just fine.
For (2), our attainable outcome distributions are now distributions over rather than over or - all along these have been 'distributions over whatever the utility function is allowed to care about', and now that doesn't (necessarily) factor in such a way. is allowed to map arbitrary combinations of to the same outcome.
In other words, there are still universal preferences for exactly those information structures which yield strictly larger sets of attainable outcomes, but with outcomes now coming through the world.
However, prong (1) is trickier. While it's easy to find sufficient conditions for to yield more attainable outcomes than (as the conditions from the original or good-regulation orders still work), it's harder to give meaningful necessary conditions. This is essentially because and can yield some of the same outcomes, and be equivalent for some purposes, without being globally equivalent. We can say that for all , there must exist some such that but not necessarily that and have some simpler linear relationship. While there is likely more to say here, I don't know that (1) has a straightforward equivalent.
Then for now all we have is:
Proposition:
Define
The following are equivalent:
- for any
- For any and , we have
When they hold, write .
The fact that universal preferences are less simple for arbitrary is exactly why they can now start to exhibit more different behaviors.
5. Example (universal) convergence behaviors
On that note: let's now look at some possible convergence behaviors, as we vary the world. It's possible to control these behaviors quite a bit, even if we still only consider the preferences shared by all utility functions.
5.0 Redux: simple divergence and simple convergence
First, the convergence behaviors of the Blackwell and good-regulator settings are of course still possible. This will happen if our 'extra shared structure' doesn't actually add structure after all, or if it adds only GR-type structure.
That is, if with , then we are in the base setting and there is no "non-trivial" convergence. Similarly, if there exist , such that and , then we are in the GR setting with "simple" convergence at the critical size , and variable but rapid divergence below.
5.1 Multi-capacity convergence
A new behavior in this setting is universal convergence at multiple scales.
Consider
with
The environment has two dimensions, one of size 4 and one of size 5. Each action has a 'kind' , a 'condition' , and a 'target' - when value of matches the th dimension of the state, the result is the 'target' state , otherwise the result is the null state . However, actions of kind 1 are fallible, and have a 1% chance to map to null state anyways. That is: the first dimension is smaller, so its conditions can be matched using a smaller partition, but it is less reliable.
In this setting, dividing along the first dimension is uniquely dominant among partitions of size 4, while dividing along the orthogonal(!) second dimension is uniquely dominant among partitions of size 5. For any state you might prefer, those partitions allow you to get the most of it (and there is no tradeoff among less-preferred states). This example can be extended to get arbitrarily long orthogonal chains of uniquely dominant partitions at different sizes.
We can also imitate this behavior using a fully deterministic [13].
5.2 Capacity-dependent convergence and divergence
We can also have different convergence behaviors at different scales - including abstractions that converge at one capacity, but diverge non-trivially at larger sizes.
Consider
with
Again dividing along the first dimension is uniquely dominant among partitions of size 4. However, there is no partition of size 5 (or 6..13) which dominates all others: if most prefers , then it will most prefer separating into it's own part. By size 14, the information structure can fully discriminate the states of the environment with different response characteristics, and there is once again a single dominant information structure.
We can glue multiple copies of this and the previous example together - leading to convergence and divergence at different scales of our choice.
5.3 Discussion
Overall, by funnelling all through the same outcomes , many of the behaviors that could hold for a single utility function in 2. can now be made to hold for all utility functions in an appropriate world.
A few things to highlight about example 5.2:
- It leads to convergence at an agent capacity much smaller than perfect information about the system. (Suggestively, the setting 'almost' factors as a GR-type system at that smaller size, plus some additional restrictions on the allowed )
- With the values we've chosen, the returns to capacity past that point are comparatively flat, and account for only a small share of the total attainable utility (for any on this environment).
- The optimal partitions of size 5+ are all refinements of our convergent partition at size 4.
This is the kind of behavior we'd need to see for practically useful natural abstractions, and given the right (bounds on a) cost function for capacity would lead to the same or similar information structures for many .
Of course, this just shows 'if we deliberately force our environment to exhibit convergent abstractions, then we get convergent abstractions'. We can also have no convergence, or convergence within a particular capacity range that shifts to a different convergent abstraction at a higher capacity.
This is all right and proper - the existence of natural abstractions is supposed to depend on specific kinds of regularity in the environment. This version of the formalism has made it possible to get convergence, but the real question is what realistic conditions on the environment would produce what behaviors. We've also confirmed that it's at least possible to come up with environments which produce abstractions that depend on the agent's capacity. To claim that differently-capable agents will use the same abstractions (if we care to[14]), we'd need to find conditions which rule that back out.
The shape of the examples also hints that while it's possible for abstractions of different sizes to be unrelated, it's probably not too hard to come up with conditions such that they 'usually' aren't. At the same time, it's not clear that realistic conditions would imply this never happens.
6. Beyond universal preferences
But before we go further on that front, let's develop a more granular and more practical means of comparison than 'preferred by all utility functions'. We want to be able to notice when 'most' utility functions share a preference, even if not strictly all.
If we want to talk about preferences 'many' or 'most' utility functions, we need a way to measure them. What should this be? Well, for any given application, what we really care about is the probability measure coming from our beliefs - for example, if we're interested in a potential agent created by some training procedure, then we care about our subjective distribution on given that training procedure. But we don't know at this point what that will be, so we are interested in results that we can either parameterize by our probability distribution, or that hold for some class of distributions.
It's... not actually quite redundant to look at what's true for all distributions, depending on what questions we ask; but for the most part this is covered by our discussion of what's true for all utility functions (consider the trivial distributions which assign all measure to a given ).
Our first step will instead be to look at 'uninformative' distributions which are invariant under particular symmetries of the problem. To do so, we'll apply ideas from Turner's power-seeking work.
We won't exactly follow the formalism of Parametrically Retargetable Decision-Makers Tend To Seek Power, for the key reason that their central relation describing "inequalities which hold for most orbit elements" is not transitive. But several parts of this section will closely parallel their results (and at one point we'll directly apply a lemma from this paper). Apart from the issue of transitivity, we'll make some slightly different choices in coverage and presentation, generalizing in some ways, while (for expedience) losing generality in others. Properly reconciling these is a topic for another post.
(Side note: it would also be natural to look at the 'maximum entropy distribution over all utility functions' in particular. We need to be slightly careful about what exactly this is[15], but presumably one can show that for this case, information structures are preferred in direct proportion to their mutual information with the outcomes. We won't pursue this here, as it would take us a bit off-track, but leave it as a conjecture.)
6.1 Dominance for all distributions from a class
Once we're measuring according to some distribution , there are a few natural questions we might ask in order to compare information structures and in terms of this measure, including:
- For what measure of is ?
- For what measure of are v.s. optimal for , out of some class ?
- How does the expected value of compare to , averaging across ?
In particular, we might wonder: can we get preorders out of these conditions which parallel the Blackwell and Blackwell-like orders, but allow for more granular comparisons?
For 1), it turns out the answer is no: comparing and in terms of the measure for which leads to a non-transitive relation even for individual (symmetric) distributions over . That is, writing for , there can be cycles[16] with , but . The same holds for defined as ).
However, the latter two don't have this problem: the probability that is optimal out of , and the expected utility , are functions from individual information structures to . Thus, for any given , they induce a total preorder on them. This allows us to safely define a preorder by intersection - for example, if for all in some class .
We'll then see how these preorders correspond to bounds on ratios of probability-of-optimality and expected-utility between and .
6.1.1 Dominance for -invariant distributions
In particular, we'll look at the relationships between and in terms of the symmetries satisfied by ; that is, we take the class to be "all distributions satisfying a given symmetry".
We can then give simple sufficient conditions and (weaker) necessary conditions for to be preferred to over all such distributions, in the sense of higher expected value and higher probability of optimality. First, will be always preferred to if we can imitate its outcomes up to a symmetry - this direction is the same essential idea as Turner's power-seeking results. And in the opposite direction, if is preferred for all symmetric , then each outcome attainable by all permutations of must be imitable by some mixture of permutations of .
To state this formally, we'll need a few preliminaries.
Given a subgroup of the symmetric group with action on , we can take it to act on utility functions, by permuting the utilities assigned to each state. This has[17] the effect that .
Then, we can define:
Definition: -invariant distribution
Define a -invariant distribution to be a probability distribution such that it's density (a.k.a. ) satisfies for all and all .
Now, distributions are just vectors in which sum to , so we can consider the action of on them as well[18]. We can naturally extend this action to sets of distributions over , such as our attainable outcome distributions, by .
Finally, we'll write , so that .
Then our sufficient condition (for the general setting) will be the following:
Theorem (-covering of outcomes implies score-domination under -invariant distributions)
Suppose for some . Then:
- for all
- for all -invariant
Write when these hold.
Additionally, let be a set of information structures with outcomes closed under the action of : if , then for all , for some .
Then:
- for all
- for all -invariant
Write when these hold.
In fact, this holds for the expectation of any 'scoring function' mapping a set of attainable outcomes (or information structure) and a utility function to a real number, which is
- monotonic in the set (i.e. implies ), and
- invariant under joint action of (i.e. ).
The proof follows more or less immediately from these properties, so we leave it to an appendix.
In the other direction, our necessary condition (which we'll state just in terms of expected utility) is:
Suppose for all -invariant .
Then
Proof: Suppose the contrary, and take . As in the Blackwell order proof, we can take a hyperplane which separates and , giving a which prefers to any point attainable by any . Now is attainable by each , so for any , and hence certainly . Therefore for uniform over the orbit of - a contradiction.
In a narrow sense, this is strict, as we can find counterexamples with even if of the orbits of each point in are contained by every orbit of . However, there should be a related necessary-and-sufficient characterization, giving a proper generalization of the Blackwell Informativeness Theorem; we set this aside for now.
Additional results for the Blackwell setting
To further show how this is all still connected to the Blackwell order, let's also give conditions corresponding to prong 1) of the Blackwell Informativeness Theorem, for the traditional Blackwell setting where and .
Suppose acts independently on each of and - and permutations of are in fact always irrelevant (when we allow all policies), so equivalently it acts only on .
Then our sufficient condition
is equivalent to[19]
for some stochastic map and
This is because here the action of on an outcome distribution is just a relabelling of , and we can[20] equally perform this relabelling before applying . In fact, this characterization will work whenever we can define an action of on and such that 'commutes' with , in the sense that (which will not in general be possible).
When is the full symmetric group , this means that all information structures with the 'same weight distributions' across signals are equivalent - for deterministic partitions, this is 'the same set of part sizes'.
Beyond the independent case, when acts arbitrarily on and can permute action-values across states, then the condition on is less obvious, though we can at least show it is a) nontrivial, b) different from the independent case, c) likely some form of majorization condition[21]. We also set this aside for now.
Finally, we'll note that our necessary condition can be translated to a similar form, but doesn't appear particularly enlightening[22].
6.2 Quantitative dominance
At this point, we've found a kind of superiority weaker (and so more general) than 'preferred for all possible utility functions', but we still haven't moved beyond a binary 'preferred' or 'not preferred' relationship for .
To do so, a natural idea is to move from simple inequalities to inequalities parameterized by a scalar - for example, defining by and similarly for . This clearly gives another preorder, and is a perfectly reasonable way to compare information structures under a particular distribution . But taking a lower bound such that this holds for all symmetric distributions is not actually interesting: if we take a trivial , for all , then the expectations will just be equal, making always 1.
However, we can define a related relationship with less trivial bounds:
Define to mean .
Note that this is equivalent to for exactly , but not otherwise.
It's less obvious that this relationship is transitive, since we take the expectation over a different conditional distribution for each pair , but it turns out to in fact be the case[23].
For this relationship, we can define to mean for all -invariant , and have this be nontrivial for .
Multiple -injections
It's also this relationship which we can infer by generalizing the previous result about -injections (paralleling the move from simple- to multiple- retargetability in the parametric retargetability context). Intuitively, if there is not just one copy of within via , but 'distinct' copies under different , we should be able to say that is not just 'at least as good as ' but ' times better than ' in some way. However, we need to be a bit careful with the details.
For this part, we'll apply a lemma from Turner & Tadepalli on "orbit-level tendencies" directly, and give the results only for .
Specifically, for our family with , we'll additionally require their conditions[24] for "containment of set copies" (Definition A.7):
We say that contains copies of when there exist such that
a)
b) are involutions:
c) fix the image of other : for
Then by their Lemma B.9, we conclude that for any (or in their notation, , interpreting once again as ). Since the value of is in , this immediately gives us[25] that where . Since this holds for the orbit of any , we can conclude that .
That is, we have the following theorem:
Theorem
Suppose contains copies of via .
Then .
The conclusion in english: according to any -symmetric probability distribution, it is at least times more likely that is optimal while isn't, than that is optimal while isn't.
While somewhat limited, this result gives us an initial scenario where we can establish a kind of quantitative dominance of one information structure over another, for a broad range of distributions of utility functions. The theorem can surely be improved; but for meaningfully stronger conclusions, we'd require stronger assumptions about the environment or the utility function distributions.
6.3 Blackwell-like relations correspond to ratio bounds
So far, we've framed our results in terms of various preorders on information structures. Mostly the intuitive meanings of these "" relationships are basically their definitions. But to make it clearer what they mean in terms of "convergence" of abstractions, especially for the quantitative relations, we'll mention another interpretation here: each relationship corresponds to a lower bound on a ratio of some quantities related to and .
The original Blackwell relation , which states that for all , implies that for all - with the corollary that e.g. for any . Likewise, and imply the same for (and distributions of ) defined on a system or a world .
Then, a relation corresponds to the bound for all -invariant .
And moving to our quantitative relations corresponds to changing the bound from to . The hypothetical would correspond to a bound - for the probability of an event (such as optimality with respect to ), this corresponds to a lower bound on the likelihood ratio of the events, e.g. . However, these are exactly the relationships that we found it wasn't possible to guarantee (for ) for arbitrary symmetric distributions; which means there is no nontrivial bound on likelihood ratios with our assumptions (recalling e.g. the trivial but symmetric , ). It would be possible to get such bounds, but it would require a different type of assumption on .
Finally, our substitute relations like correspond to bounds on more unusual ratios of the form: When is a binary indicator of an event like , this gives likelihood ratios like: .
This unusual likelihood ratio highlights that "contains multiple copies"-style relations don't necessarily give us as strong of a form of convergence as we might hope: while they can tell us is at least times more likely than , they can't unconditionally tell us that e.g. is times more likely than over a symmetric distribution.
Perhaps a simpler takeaway from these bounds is this: if you can find a so that the values of for and are never equal at any point in it's orbit, then the expectation for is times greater than for . That is, if for all , then . If such a exists, there will be some -symmetric distribution where , though it need not hold for all of them.
7. Discussion
7.1 The Weak Natural Abstraction Principle
A (much) weaker version of the natural abstraction hypothesis would be just: "some abstractions are usually preferred to others" [by most agents, in natural environments]. In this form it is obviously true; if nothing else, surely we can come up with some abstractions which are quite useless, and some which are not. As we advanced through the post, we emphasized how we weren't yet able to guarantee strong convergence of abstractions, such that most agents prefer only a "small" number of natural ones. However, we can also see the theorems of this post as providing gradually stronger demonstrations of this weak natural abstraction principle (for our setting).
Already from the original Blackwell Informativeness Theorem, we saw that some information structures are strictly preferred to others (in the sense that and ) - those providing a superset of information about the world, and so a superset of attainable outcomes given that information structure. Through the GR and W settings, we saw that if there is non-trivial structure to the environment's "outcomes" (which agents are allowed to care about), then information structures need only provide a 'dominant' set of information relevant to controlling these outcomes. This still requires enabling a superset of attainable outcomes, but environmental structure makes this relationship more common. Finally, by moving from 'preferred by all' to 'preferred by more', we saw that the requirement could be softened from 'a superset' of outcomes, to 'unambiguously more' outcomes (in the sense that we could get a superset up to a permitted relabelling of outcomes).
Even the first type of relationship is guaranteed to exist in any nontrivial environment, and so to guarantee us common preferences: bigger information structures with more information will be preferred to similar smaller ones (as long as both are smaller than the whole environment). But this doesn't really capture the spirit of the natural abstraction hypothesis. It tells us nothing about preferences between information structures with the same amount of information, or different amounts of distinct information. By the final case, however, we get something more in the right spirit: as long as the environment has at least some information which is more relevant to controlling outcomes than the rest, there will be convergent preferences towards abstractions which capture that information. Many more abstractions can be compared in terms of 'how much' policy-relevant information they provide.
We've then essentially proven an especially weak (and indeed 'obvious') form of the natural abstraction hypothesis. The setting where we prove this is bare-bones, but correspondingly universal: while there are many other elements we'd want to include for a more thorough study of abstractions, basic preferences over 'ways of coarse-graining information' will still apply.
Of course, it's only stronger forms of the hypothesis that would be of much practical use for alignment. Rather than "some abstractions are generally preferred to others", we'd need something more like "most agents will converge on a 'small' number of discrete potential abstractions[26]". To have a chance to get a result like this, we would need to introduce some of those missing elements.
7.2 Weak natural abstraction as power-seeking
Intuitively, there's a clear connection between natural abstraction and instrumental convergence: where natural abstraction proposes that certain 'abstractions' are more useful to a wide range of agents (in a given environment), instrumental convergence proposes that certain states or actions are more preferred by a wide range of agents. Since here we have a formal working notion of 'abstractions', as information structures, we can make this connection more explicit. Indeed, in our power-seeking-theorem style analysis, we basically already have - but let's see directly how convergent preferences over abstractions can be seen as a special case of power seeking.
Recall that 'power' in the sense of these theorems is a concept about the choices available to you, so 'seeking power' only makes sense if you are making at least two successive choices. We're then looking for a sequence of choices which occur in our setting - which are, naturally, 1) your choice of information structure , 2) your choice of policy given the information structure.
We can choose to view this as an a two-timestep MDP, with choice of leading to a dedicated state , and choice of leading stochastically to an outcome via . Intrinsic reward for each information state is 0, and the reward of an outcome is it's utility[27].
Then, the standard power-seeking results applied to this MDP[28] tell us that most parametrically retargetable decision-makers (including but not limited agents choosing according to some utility function) will 'tend' to choose information structures which give them 'more' attainable outcomes via their choice of policy, and hence have higher 'power': higher average optimal value[29] attainable from that state, averaging over utility functions.
The original versions of these theorems give us this 'tendency' in a slightly different form than we've used here ("a larger number of orbit elements of a decision-making function which strictly prefer one information structure vs. another"). As discussed earlier, we deliberately use a different formulation to ensure our tendencies (common preferences) are transitive. But up to this reformulation, which could equally be applied to the general power-seeking context, these results are exactly the same ones we saw in section 6.
We can then say that "weak natural abstraction [exists, and] is equivalent to power seeking tendencies in the agent's choice of abstraction", and prove it in a particular formal sense. Tendencies towards preferring certain (natural) abstractions occur exactly when instrumental convergence occurs in an information-selection problem derived from the environment.
7.3 Limitations and future work
We've built up one step at a time, from the minimal possible setting and the simplest questions. As a result, we've so far ignored many key aspects of realistic abstractions. We'll briefly go over a few of the most important missing pieces of the story, and how they relate to this framework.
-
The first missing piece can be summarized as: we ignore "internal" and "local" structure of all kinds. We treat the environment, signal, actions, and outcomes as undifferentiated sets - we don't factor them into variables representing e.g. different parts of the environment, and relate such structure to the mappings between objects. Relatedly, we don't consider any notion of 'similarity' between different world states, signals, or objects. As an important special case, this includes a lack of any real temporal structure.
The real 'substance' of the natural abstraction hypothesis is about the structure of the environment. Local structure is key to stories of why natural abstractions should exist, and what kind of thing they should be - for example, "information relevant to 'far away' variables" inherently requires some notion of distance (usually, a distance in a causal graph). This is well motivated by the local causal structure of the real world. But local structure in the signal and the encoder may also play an important role. For instance: this is what's is required to represent ideas like "similar world states are encoded by similar signals" or "a particular 'part' of the signal always corresponds to a particular 'part' of the environment". Moreover, the signal and encoder will also be embodied in the physical world. I expect such structure may be necessary to properly understand e.g. the modularity of abstractions.
Introducing internal structure to the environment is the main bridge to Wentworth's work on abstractions, and an obvious next step[30]. Introducing internal structure to the agent and it's boundaries is less-explored, but likely important. This is also where we would model distributions over functional behavior pushed forward from distributions over parameters, via some parameter-function map.
-
Second, we touch only very lightly on similarities between abstractions. Of course, we should care not only whether different agents use exactly the same information structures, but also if they use 'similar' ones. While internal structure opens up more options, we could look at extrinsic similarities even using only the current setting. 'Contains a superset of the information' is one relationship of this type, and we mention in passing 'orthogonality' of deterministic information structures, but there are many more possibilities (starting from mutual information - but this alone doesn't constrain 'what' information is shared).
-
Third, we've ignored all computational aspects of the problem - and thereby any 'reasoning'. The message-size of an abstraction can be considered a particular kind of space complexity, but there are many other tradeoffs - we may be concerned with the the algorithmic (or circuit, etc.) complexity of encoders and policies, as well as of the problems of selecting them. In principle all of this could be cast in terms of cost functions on internal structure, but is also well worth considering from an abstract computational perspective.
-
Finally, we assumed throughout the optimal choice of policy; and towards the end, we considered optimality with respect to a set of information structures. These can (and should) be generalized from optimality to other criteria. Some of this generalization can be transferred directly from the parametric retargetability setting with a little more care (though there are some details to watch to maintain transitivity). While part of the motivation for non-optimal choice can be addressed through appropriate costs on structure and computation, it is also simply worth generalizing beyond deterministic selection.
A convenient property of our setting is that it's fairly clear how one could add all of these pieces.
7.4 Additional remarks
A few other miscellaneous remarks:
-
Adding a lossy 'perception' between and (i.e. ) so that doesn't have direct access to the environment does nothing more, nor less, than restricting the space of possible information structures. Namely, it restricts to those of the form , a.k.a. those in the cone .
-
Transferring some of the ideas here back to the general power-seeking context, we can observe for example that a) while no individual action strictly dominates any other, some sets of actions can strictly dominate other (even disjoint) sets, b) a state can be strictly preferred to not just over all distributions symmetric under the permutation of every state, but even over all distributions (or ) symmetric only under interchanging the values of and .
-
Another way to view this whole setting is as a problem of lossy compression, which we can analyze through rate-distortion theory. Our interest is different from the usual applications rate-distortion theory in that we're interested in commonalities between the encoders for broad families of abstract "distortions" (derived from utility functions) which may not have anything to do with 'reconstruction', as well as that we currently consider only a single timestep. But similarities among distortion-rate functions for different distortions, especially e.g. phase changes at consistent capacities, may certainly be relevant.
8. Conclusion
We started with a simple formal model of abstraction, where an agent must coarse-grain information about a larger environment into a smaller number of internal states. In this model, we asked: when do different agents prefer to abstract in the same way?
We found that while there are few preferences common among all general-form utility functions, as we add more structure to their domain, we can get proportionally stronger convergence. When restricted to preferences over a shared environment, all agents may prefer exactly the same abstractions - or indeed completely different ones, depending on the environment. We gave examples of several possible convergence behaviors, including cases where abstractions converge strongly at particular capacities, but are orthogonal across capacities. We then generalized these results, using a modified version of Turner's power-seeking formalism to show that many more preferences are shared by 'most' utility functions, under priors obeying certain symmetries. Based on this, we showed how natural abstractions can formally be viewed as a type of power-seeking.
Some high-level takeaways:
- For agents facing the same environment, there is indeed almost always some convergence in preferred abstractions. How much depends on the environment, and the relationships it creates between the attainable outcomes using different abstractions.
- Even if an environment leads to convergent abstractions, there's no general reason why it can't lead to unrelated abstractions for agents with different capacities. Quite likely, the same is true for other differences in constraints. There are arguments[14:1] why this might not a problem, and there may be conditions which prevent this from being an obstacle in practice, but we so far lack a formal model of this.
And a meta takeaway: taking the perspective that 'abstractions are ways of coarse graining the environment' literally and building a straightforward model of it gives a very tractable setting, with connections to many established fields. By default it lacks key features we'd want to fully model abstractions, but it comes with handles to introduce several of them.
Overall, even if the strongest (and most convenient) forms of the natural abstraction hypothesis turn out to be false, there will surely be some degree of convergence among the abstractions used by different agents in practice. Understanding the factors behind this convergence, and behind the formation of abstractions generally, would be useful in order to know what to expect of AI systems. Even short of strong natural abstractions, these dynamics inform the viability of different interpretability and alignment techniques - under what conditions we can trust them, and when we can expect them to generalize. Furthermore, they have multiple connections to the dynamics of which goals agents will acquire (i.e. agent-selection-processes will bring about) in which circumstances - of obvious importance.
While the theory here is only a very early step, we hope it can help clarify some of the broadest strokes, and show directions for further development.
Appendix: Omitted Proofs
Proof of "-injection of outcomes implies EU-dominated under -invariant distributions"
Let be a function which scores a set of attainable outcome-distributions against a utility function, so , with the following properties:
- Monotonicity: if , then for all .
- -invariance: for all , and , we have
Then also naturally scores information structures, by .
Lemma: If , then .
Proof: We have , with the three equalities following from -invariance, the sum being over the same orbit, and monotonicity respectively.
Corollary: For any -invariant distribution over utility functions, .
Proof: Since each element of the orbit of any has the same density , the expectation is unchanged if we replace by its average over the orbit : The lemma says that at each point, so (and in fact the converse also holds: if this is true for all -invariant , then we must have for all .)
Then to complete the theorem, we just need to confirm that is monotonic and -invariant for any , and so is the optimality of out of a -symmetric set of options[31] : , which are easily checked.
Specifically, in terms of theorems,
- The Blackwell Informativeness Theorem and Good Regulator Theorem are of course far from novel
- Somewhat to my surprise, I haven't been able to find the "GR-Blackwell Order" result anywhere. Still, I wouldn't be shocked if an equivalent result had come up in some other context. The connection appears to be new - there seem to be no sources at all which discuss both the Blackwell order and the Good Regulator Theorem.
- The power-seeking + Blackwell results I expect to be novel. The modified formulation of the power-seeking results is also novel.
And more confidently: we can at least say that this is an important facet of the agent's abstractions. ↩︎
Suppose , with (since , if one coefficient is strictly in then two are). Let be the optimal policy for . If , then with does at least as well; if then does. This has reduced the number of coefficients in by at least 1; repeat until there are none. If any of these -inequalities are strict, than is strictly preferred. Suppose they are all equalities; if for any , then we can combine those signals and get a smaller ; if not, means that is indifferent between distinct outcomes. ↩︎
And again, any fixed nondegenerate prior would also work. ↩︎
We use two types of diagrams in this post. The first is the "graphical model" style (as e.g. in section 1), and the second is commutative diagrams (as here). We mention this because the same picture would mean something completely different as a graphical model vs. as a commutative diagram. We use boxes around the nodes in graphical models, and no boxes in commutative diagrams. ↩︎
In other words, each state has positive measure for some some : ↩︎
To be a little bit more explicit about how the 'multiple agents' vs. 'multiple games' interpretations relate here:
- " is preferred for all " " is preferred for (all individual agents facing) arbitrary distributions over "
- " is optimal for all " " is optimal for some distribution over with full support" (for optimality with respect to any upward-closed universe of information structures).
- However, may be preferred by a particular distribution with full support without being preferred by all , and may be optimal for the distribution with respect to a non-closed set of information structures without being optimal for any .
We use 'all tasks' instead of the Gooder Regulator Theorem's 'a sufficiently rich set of tasks' - which turns out to mean exactly 'a set of tasks equivalent to all tasks for the purposes of this system'. As a side effect of our re-proof of GRT, we'll be able to get the corollaries a) such a set of tasks exists, b) for a set of tasks to be sufficiently rich for all possible systems, it must be dense in the set of all tasks, c) for a single system, tasks suffice (a loose bound). ↩︎
This follows from the fact that column normalization is equivalent to multiplication on the right by an appropriate diagonal matrix, which is invertible. ↩︎
Picking any (consistent) arbitrary value of the if there is more than one. We will assume this throughout. ↩︎
Consider which all map onto a 1-dimensional line - merging any number of pairs of adjacent states gives a Pareto partition for its size, and these are the only ones. For illustration: let be distributions over ); then and are Pareto optimal, but is not. This is the smallest possible number of Pareto partitions for a given . ↩︎
N.b. we say 'world' rather than 'world model', because this defines the dynamics of the external environment, not an internal representation the agents might form of those dynamics. ↩︎
Add an additional dimension , and make only (with ). Then you get a unique family of dominant partitions of size , with the states divided along the first dimension, and the states assigned arbitrarily to those parts. But these partitions are all equivalent to each other under all , so there is still only one dominant equivalence class. ↩︎
On the other hand, perhaps we don't care if differently capable agents 'use' the same 'abstractions' in the first place, for the senses in this post.
Wentworth gives the example of DNA: we can recognize and reason about how a tree-DNA-sequence-distribution screens off certain information between specific trees without containing the tree-DNA-sequence-distribution itself in our heads. This demonstrates that the agent need not - simultaneously and non-counterfactually - contain the information of the low-dimensional summary for it to be relevant; the naive 'size of the abstraction' isn't necessarily binding.
Seems intuitively compelling; does this solve the whole problem? Do we still need to worry about sufficiently large/complex concepts such that we can't even store their index, or concepts with insufficiently simple/factorable implications, or other cases where perhaps this fails?
Well, we should build some models of how exactly this works and try to find out. So far I have only vague ideas for how to do that, but you'd certainly need many kinds of structure we haven't yet included. ↩︎ ↩︎
Rather than e.g. assigning each state utility to be IID uniform on , as some have used, I think the more natural maximum entropy distribution is to consider utility functions as 'directions' (given their equivalence up to affine transformations), and so take the uniform distribution over the -sphere. This turns out to be equivalent to taking each state utility to be I.I.D and renormalizing. ↩︎
Essentially: even for with the same orbit of utilities, the tuples of utility values for different permutations can be aligned like , , , such that each dominates than the previous under most permutations (i.e. is greater at most indexes of the tuples). This follows from a similar pattern in the maximum attainable share of different outcome vectors. As concrete example: let , , , and with the uniform distribution over all possible assignments of utilities to outcomes (so that ). A computer evaluation confirms that we then have , but . ↩︎
If you like, from , where we once again consider as a vector . ↩︎
In order for to be closed under the group action, and for the action to be linear, it turns out must act only by permuting the elements of - this is one reason we must require to be a subgroup of rather than the orthogonal group . ↩︎
Compare this to the alternate form for the GR-Blackwell order in section 4.1.1: both involve compositions on the right of , but in the GR case we apply a fixed homomorphism before both and , while here we look for the existence of an isomorphism asymmetrically. ↩︎
The elements of are where . This is exactly the elements of - as is a bijection on the set of all policies, the union over all and over all is the same. ↩︎
In the case where , restricting to deterministic , we can show that a) the orbits of certain disagree on preferences between some , so not everything is equivalent (and also the relation is not a total order), b) if you shift a element from a larger part in the partition to a smaller part, the resulting partition is at least as good - and therefore, a sufficient condition for is that the vector of part sizes for majorizes the vector of part sizes for . This is definitely the kind of thing that can be expressed by some stochastic matrix equation, but I'm not sure what the exact condition is for general - perhaps something like for column-stochastic and doubly-stochastic . The difference between orderings under independent vs. joint permutations appears to parallel the refinement vs. dominance orders on integer partitions. ↩︎
I believe it translates to: "Suppose for all -invariant - then if there exist stochastic such that for all , there must also exist stochastic and , such that ". ↩︎
This comes down to the lemma: if and , then . Presumably there is some nice proof of this, but you can also see that it will be true by drawing as overlapping collections of line segments, and prove it by solving the constrained minimization of . ↩︎
Intuitively it should be possible to weaken the involution condition, which constrains our choice of , but it's not immediately obvious to me how. Something like "the send to ", which is one of the things the original conditions accomplish, and with c) we then further have " are disjoint", but there may be some additional requirement. ↩︎
This observation, together with the transitivity of , shows that in fact Turner's orbit-level tendencies are transitive for binary functions. ↩︎
Or at least a manageable number of manageably-low-dimensional manifolds of potential abstractions. ↩︎
Writing slightly loosely, ↩︎
To be clear, the current version of these theorems doesn't require the setting to be an MDP; but an MDP is still needed for the definition of 'power' and so for interpretation in terms of 'power seeking'. ↩︎
In our setting, a distinction between 'average optimal value' and 'average optimal value, excluding the reward of the state itself' is irrelevant, as we insist the whose power we consider have no intrinsic value. ↩︎
Arguments that 'most utility functions care only about information relevant far away, because most of the things they might care about are far away' and 'most agents care more about information the more copies of it appear in the environment' have especially clear translations. ↩︎
As - note the outcome-invariance of is necessary, otherwise the optimality indicator is not -invariant and we can find counterexamples to the conclusion. ↩︎