There is a new paper by Liu et al. that claims to have understood the key mechanism underlying grokking (potentially even generalization more broadly). 

They argue: 
1. Grokking can be explained via the norm of the weights. They claim that there is a constant level of the weight norm that is optimal for generalization.
2. If there is an optimal level of the weight norm, the weight norm of your model after initialization can be either too low, too high or optimal. They claim that grokking is a phenomenon where we initialize the model with a large weight norm and it then slowly walks toward the optimal weight norm and then generalizes. 

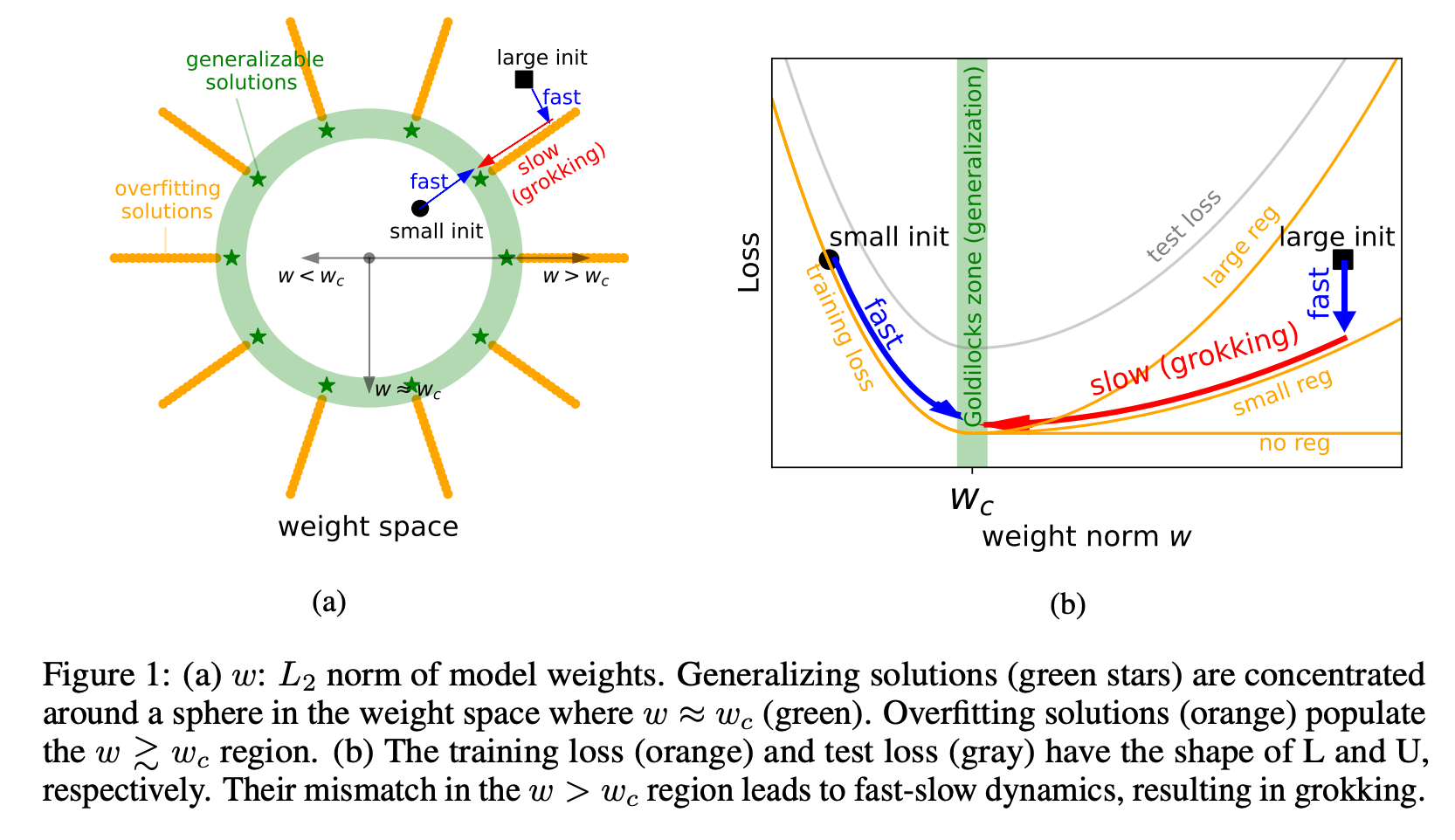
3. They also claim that you can get the same results as grokking but much faster if you set the weight norm correctly at every step.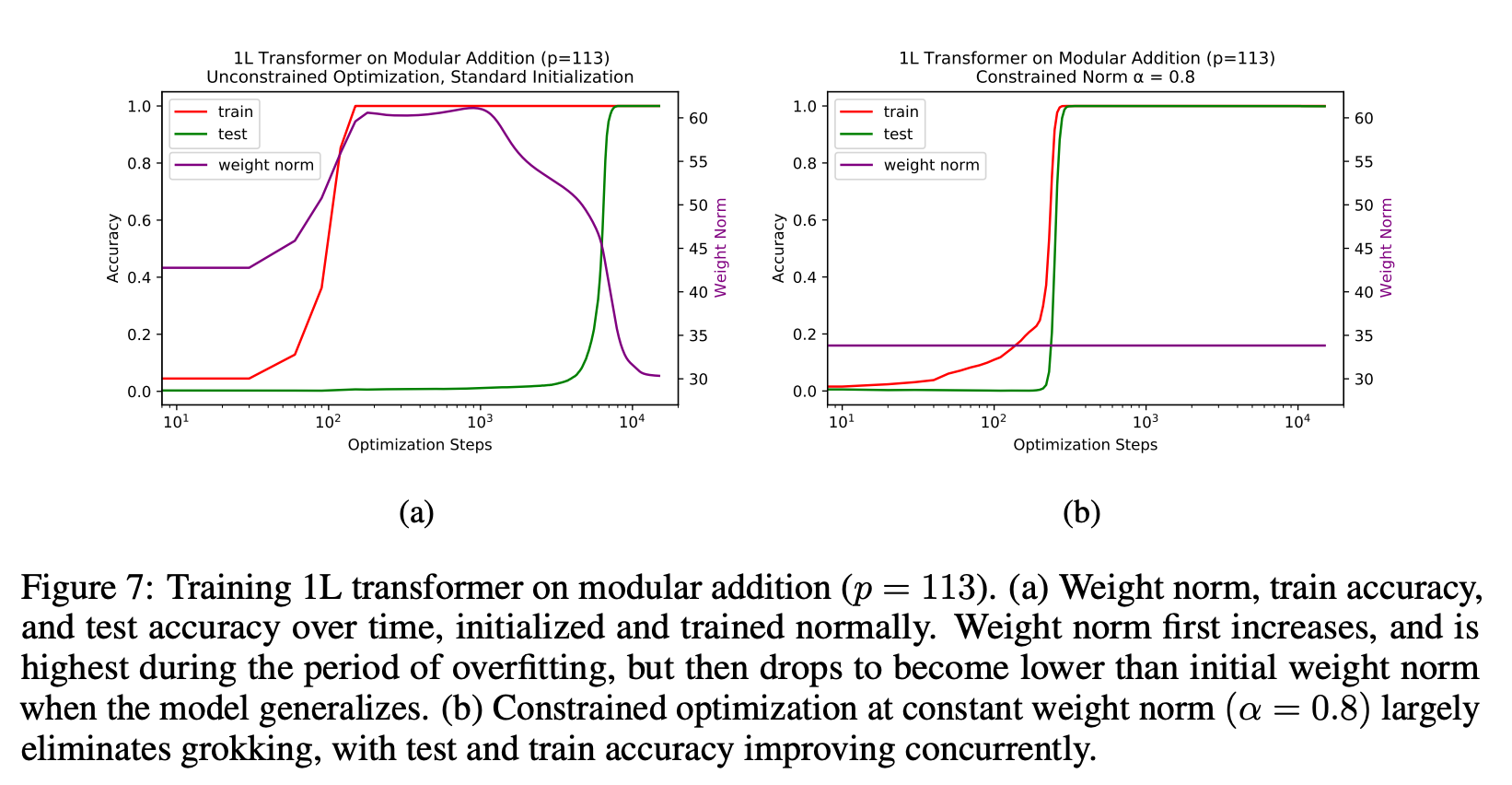

4. They set the norm "correctly" by rescaling the weights after each unconstrained optimization step (so after every weight update loss.backward()?!)

Implications:

1. I think they have found a very important insight of grokking and finding generalizing circuits more broadly. 
2. I'm still a bit skeptical of some of the claims and results. On some level "just fix your weight norm and the model generalizes" sounds too simple to be true for all tasks. 
3. I think this result could have big implications but I'm not yet sure whether they are positive or negative. On the one hand, finding generalizing circuits seems to solve some of the problems associated with bad out-of-distribution generalization. On the other hand, it likely speeds up capabilities. 

I'm very unsure about this paper but intuitively it feels important. Thoughts?