Introduction
Credal sets, a special case of infradistributions[1] in infra-Bayesianism and classical objects in imprecise probability theory, provide a means of describing uncertainty without assigning exact probabilities to events as in Bayesianism. This is significant because as argued in the introduction to this sequence, Bayesianism is inadequate as a framework for AI alignment research. We will focus on credal sets rather than general infradistributions for simplicity of the exposition.
Defining Credal Sets
Recall that the total-variation metric is one example of a metric on the set of probability distributions over a finite set A set is closed with respect to a metric if it contains all of its limit points with respect to the metric. For example, let The set of probability distributions over is given by
There is a bijection between and the closed interval which is the map that sends a distribution to the probability of zero. More generally, recall from the proof of Lemma 1 in the preceding post, that if is a finite set with elements, then there is a bijection between and the closed simplex
Consider the following subset of
The set is an open subset of in the same way that the open interval is an open subset of the closed interval (See Figure 1.) In particular, does not contain the distributions and defined by and which are limit points of For example, given the distribution defined by is an element , and the total variation distance between and is
In contrast,
are all examples of closed subsets of
We now consider the meaning of convexity in this context.
Definition: Convex set of probability distributions
A convex combination of probability distributions is a linear combination such that and A set of probability distributions is convex if it closed under convex combinations.
If a distribution is written as a convex combination of a set of distributions, then it is called a mixture distribution. Note that the definition of a convex combination ensures that mixture distributions are indeed probability distributions. Sampling from the mixture distribution can be thought of as first determining an index by sampling from the distribution over defined by and then sampling from the corresponding
As defined above, and are convex sets, analogous to how and are convex subsets of . However, is not a convex set. To see this, let and Note that is an element of and is an element of The distribution defined by can be written as the mixture distribution However, as shown in Figure 1, is not an element of so is not closed under convex combinations.
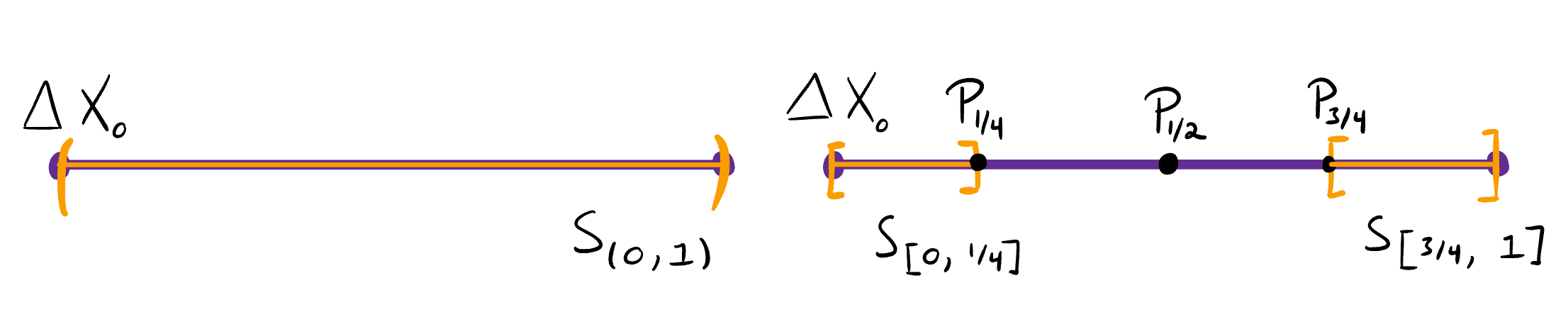
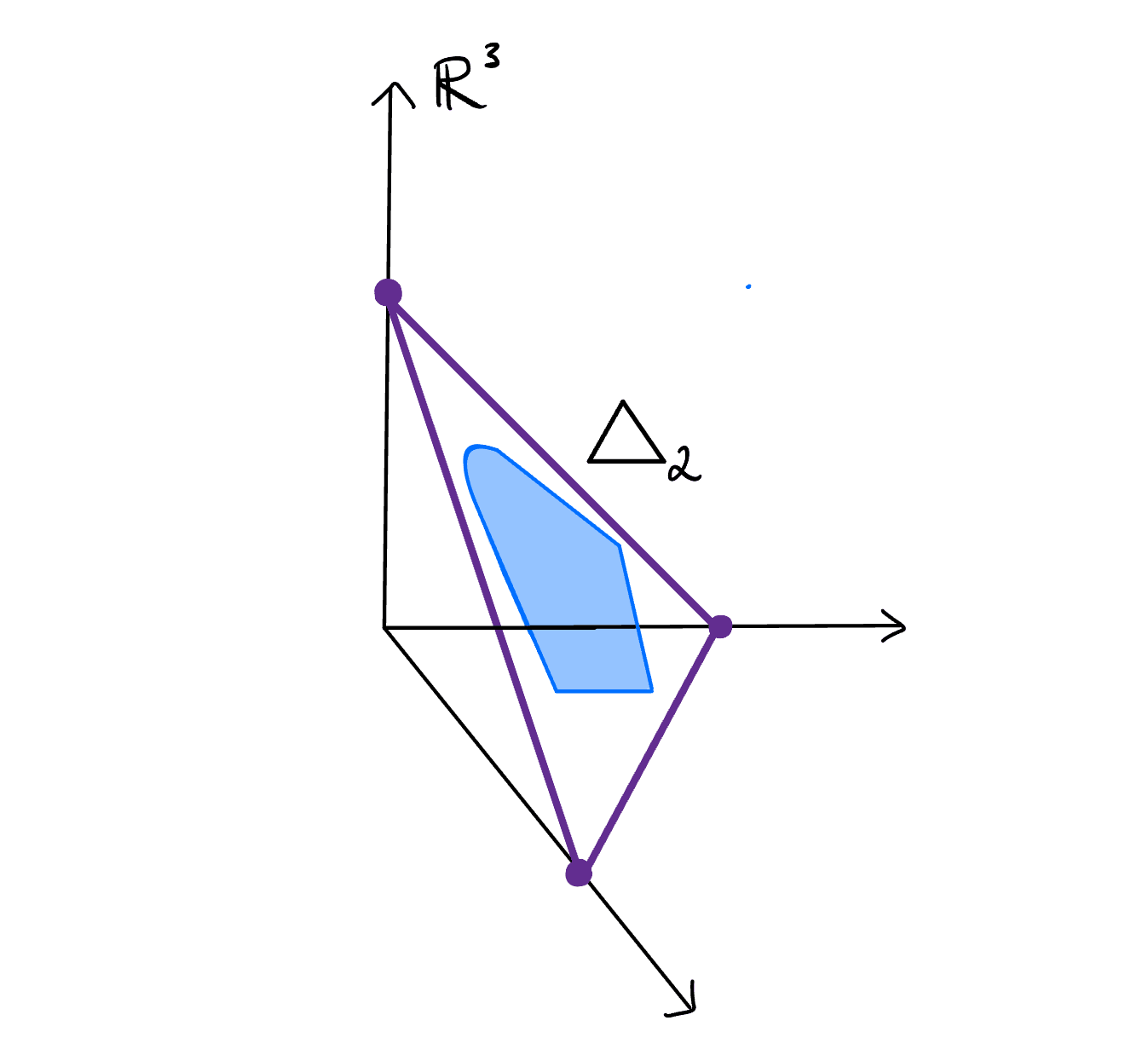
If a set of probability distributions is both closed and convex, it is called a credal set. Among the examples we have seen, , and are credal sets. See Figure 2 for another example. Since fails to satisfy convexity, it is not a credal set.
Definition: Credal set
Let be a set, and let denote the set of probability distributions over A credal set over is a closed, convex subset of where closedness is defined with respect to some metric on The set of credal sets over is denoted by
Credal sets are a natural tool for describing situations in which uncertainty cannot be reduced to probabilities. These situations are said to have Knightian uncertainty[2]. Knightian uncertainty is notably distinct from situations in which probabilities can be assigned with low confidence.
For example, in Risk, Ambiguity, and the Savage Axioms (1961), Daniel Ellsberg writes of the "Knightian urn," an urn with 100 balls in which an observer is ignorant of the proportion of black and red balls. We would say that an observer of this urn has Knightian uncertainty with respect to the events of drawing either a red or black ball. Corresponding red to 0 and black to 1, this Knightian uncertainty can be captured by the credal set as above. On the other hand, an observer may gain partial information while remaining ignorant about the remaining possibilities, such as learning that there are no more than 25 red balls. The credal set captures this partial information. In this case, we would say that the observer then has Knightian uncertainty over the elements of this credal set.
Convexity is a natural condition in the presence of Knightian uncertainty. If an observer considers some distributions as all possible and furthermore does not hold any beliefs about which distributions are more likely than others, then they should also consider any mixture distribution as possible. When the possible set of distributions is finite, this is equivalent to taking the convex hull of a finite set of points, which yields a convex polytope.
Furthermore, the decision rule discussed below makes the same recommendation for a set of probability distributions and its closed convex hull. Therefore, we can always without loss of generality assume that a set of distributions is a credal set.
Infrakernels
In machine learning classification, neural networks learn functions from sets (e.g. sets representing images) to probability distributions over possible classes; this kind of function of type for sets and is called a probability kernel. In this case, X is called the source of the kernel and is called the target of the kernel.
An infrakernel[3] is the infra-Bayesian analogue of a probability kernel. A special case of infrakernels in which the target is a set of credal sets is called a crisp infrakernel.
Definition: Crisp infrakernel
Let be a topological space, and let denote the set of credal sets over a set . A crisp infrakernel is a continuous function of type
For example, every continuous probability kernel is a crisp infrakernel since a single probability distribution is a credal set with one element.
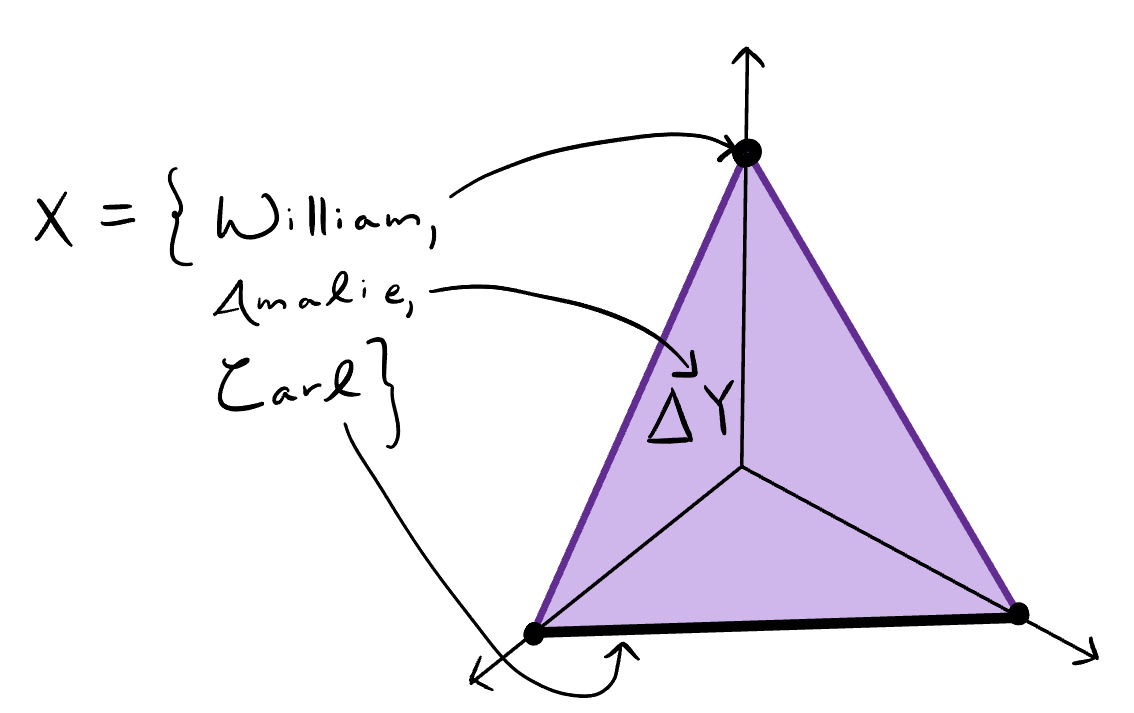
An example of a crisp infrakernel that is not a probability kernel is shown in Figure 3. Let , and let , with the elements of referring to numbers of cats. We can define as follows: is the set containing only the distribution that is one at two, is the set of distributions that assign zero to two, and is the set of all distributions over This infrakernel represents certainty that William has two cats and Carl does not have two cats, and complete uncertainty about how many cats Amalie has. Since is finite, is automatically continuous.
Deterministic Versus Stochastic Policies
In the preceding post, we discussed stochastic policies, maps of the form . Deterministic policies are a special case of stochastic policies, and can be written as partial functions of the form By partial function, we mean that the domain of the policy is restricted to those histories consistent with it. We previously observed that under some mild assumptions in the classical setting, an optimal policy exists. Furthermore, the optimal policy may be chosen to be deterministic. As we argue below, deterministic policies can be represented by stochastic policies and thus from this point forward, we will assume that policies are deterministic.
To emulate a stochastic policy using a deterministic policy, an agent can choose an element of and use a random number generator (RNG) to sample it. The output of the RNG then dictates an action. An observation from the environment then follows as usual. To formalize this, if and are the sets of actions and observations respectively from the stochastic setting, we can define a new set of observations equal to . This new set records both the action dictated by the RNG and the usual observation that follows. The new action space would be with each element of corresponding to an RNG that encodes the distribution.[4]
Importantly, this allows the random number generator to be insecure, biased, or influenced by the environment. In comparison, assuming that the set of policies is stochastic implicitly invokes an assumption that the agent can access a source of true randomness that is inaccessible by the environment. The deterministic theory not only encompasses the stochastic theory, but it is also applicable to embedded agency and can be used to solve Newcombian problems.
Topologies on policies and destinies
In this section, we review several important topologies. These topologies are relevant to how we define credal sets over the set of destinies , as we require a notion of closure in the abstract space that is
The topology on the set of deterministic policies
Recall that the set of deterministic policies is a set of partial functions The set of deterministic policies can be written as a subset of the product space where for all
We assume that is finite, and thus the natural topology on is the discrete topology. Then is naturally endowed with the (subspace topology of the) product topology that comes from the topology on This means that a basis element of the topology on has the form where for all and for only finitely many An open set is then an arbitrary union of basis elements.
Recall from Lemma 2 of the preceding post that is compact.
The topology on the set of destinies
The set of countably infinite histories , referred to as destinies, is a metric space under the metric where and is the time (index) of first difference between and In the proof section, we show that is compact under this metric.
Lemma 1: Suppose and are finite. Then the set of destinies is a compact metric space.
The topology on the set of credal sets over destinies
Recall that the total-variation distance between probability distributions and is given by A natural way to extend any metric on probability distributions to credal sets is to use the Hausdorff metric. The Hausdorff metric is a metric that can be defined on the closed, non-empty subsets of a metric space. When restricted to one-element sets, the Hausdorff metric is equivalent to the metric of the original space.
Definition: Hausdorff total-variation distance between credal sets
Let and be two non-empty credal sets. For a credal set and distribution let The Hausdorff distance between and is given by
Because credal sets are closed by definition, the Hausdorff total variation distance between non-empty credal sets is a well-defined metric.
The topology of is then given by the metric topology induced by the Hausdorff distance between credal sets.
Crisp Causal Laws
Causal laws[5] are a special type of infrakernel used to analyze sets of environments.
Given a set of environments and a policy , we can consider the set of distributions over destinies that arise from the interaction of each environment and the policy, which we denote by (for details see the preceding post).
Wrapping this into a function results in an infrakernel as follows.
Definition: The infrakernel generated from a set of environments
A set of environments generates the infrakernel defined by where denotes convex hull and denotes closure.
This leads to the definition of crisp causal laws, which take the role of hypotheses in infra-Bayesianism, as opposed to environments in classical reinforcement learning theory.
Definition: Crisp causal law
A crisp causal law is an infrakernel generated by a set of environments.
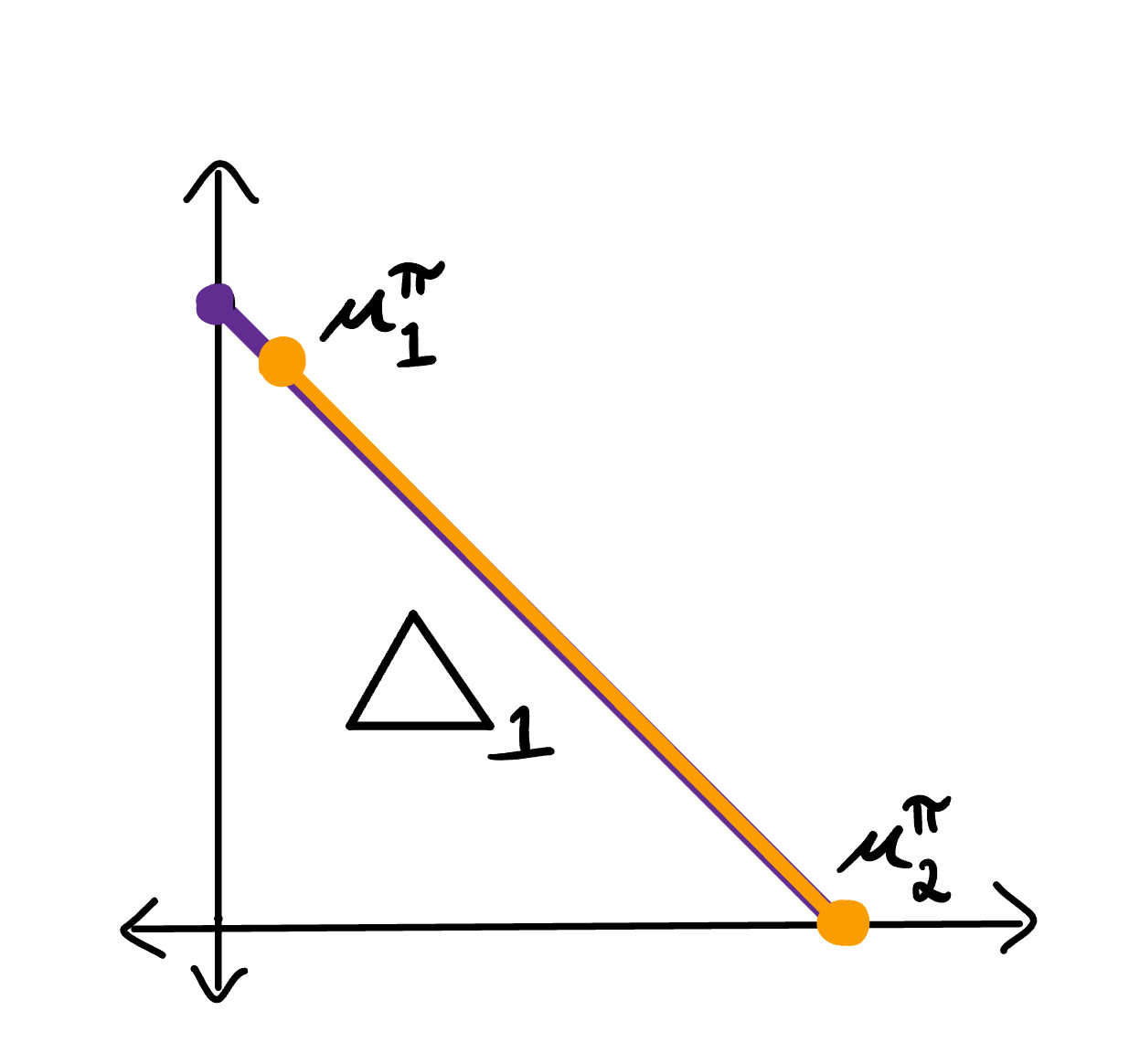
For example, let and denote a set of actions and a set of observations respectively. Let be a policy such that where denotes the empty history. Let denote an environment such that . Let denote a second environment such that . A calculation as in Figure 2 of the preceding post shows that is given by with each index of the tuple corresponding to one of the four possible histories of length one. Furthermore, is given by
By disregarding the last two irrelevant coordinates, we can visualize and as points in the 1-dimensional simplex. Let be the convex closure of . Then corresponds to a line segment on the 1-dimensional simplex as shown in Figure 4.
The next proposition states that crisp causal laws are continuous with respect to the topologies discussed in the previous section. Since we are working with topological spaces, a function between topological spaces and is continuous if for every open set in , is open in It is well known that this definition is equivalent to the epsilon-delta definition of continuity when and are metric spaces.
Proposition 1: Every crisp causal law is continuous with respect to the product topology on and the Hausdorff topology on
The Minimax Decision Rule
In the classical setting, given a set of policies and a prior over a class of environments, a natural rule for choosing a policy is expected loss minimization in which a policy is chosen to minimize expected loss with respect to the prior. Recall that crisp causal laws take the place of environments as hypotheses in infra-Bayesianism. Even if a prior over hypotheses (crisp causal laws) is given, it is impossible to carry out expected loss minimization because there is Knightian uncertainty over the distributions that make up a credal set.
Because expected loss minimization is impossible, it is necessary to use a different decision rule. In the context of AI alignment, it is of interest to have guarantees on agent behavior that hold even in the worst-case scenarios. Given a set of environments, worst-case reasoning describes a decision-making heuristic in which an agent assumes that the true environment is the environment that would be worst with respect to some measure. The minimax decision rule stipulates that an agent should choose a policy so that the maximum expected loss over the set of possible environments is minimized.[6] Other decision rules can be reduced to minimax[7], and furthermore, there are natural classes of hypotheses that are learnable with respect to minimax, a notion that we define below.[8]
Worst-case reasoning is implicitly built into the following definition.
Definition: Expected loss of a policy with respect to a crisp causal law
Let denote a continuous loss function. The expected loss of a policy with respect to a crisp causal law is defined by
Using the assumption that is continuous, Lemma 1 and Lemma 4 of the proof section imply that is well defined.
Choosing a policy that minimizes expected loss with respect to a crisp causal law is equivalent to choosing a policy that minimizes the maximum possible loss over the distributions obtained from the interaction of the policy and each environment. Therefore, the infra-Bayesian version of expected loss minimization is exactly a minimax decision.
Infra-Regret
Now that we have established the definition of expected loss in this setting, we can define the infra-Bayesian analogue to the regret of a policy with respect to an environment.
Definition: Infra-regret of a policy with respect to a crisp causal law
Let denote a continuous loss function. The infra-regret of a policy with respect to a crisp causal law is defined by
It is natural to ask whether this notion of regret is well-defined. A proof can be given using Lemma 2 of the preceding post, which states that is compact, and the following proposition.
Proposition 2[9]: Let be a policy, a crisp causal law, and a continuous function. Then the map is continuous.
In the classical theory, a prior over environments quantifies uncertainty about the true environment. The analogue in infra-Bayesianism is a prior over crisp causal laws. The expected regret with respect to a prior of this type is called the infra-regret.
Definition: Infra-regret of a policy with respect to a prior
Let denote a prior over a set of crisp causal laws. The infra-regret of a policy with respect to is defined by
Infra-Bayes Optimality and Learnability
In this section, we introduce some elementary results on learnability in infra-Bayesianism. The analogue to a Bayes optimal policy with respect to a prior over environments is an infra-Bayes optimal policy, defined as follows.
Definition: Infra-Bayes optimal policy
An infra-Bayes optimal policy with respect to a prior over crisp causal laws is a policy
A family of policies is said to be infra-Bayes optimal if for all is infra-Bayes optimal for the -dependent loss function
A natural question is: Does an infra-Bayes optimal policy always exist? The answer is yes; this is a corollary of Proposition 2 and the compactness of . A standard continuity argument can also be used to show that the set of infra-Bayes optimal policies is closed, as stated in the following corollary.[10]
Corollary 1: Existence of the infra-Bayes optimal policy
Let denote a policy, a crisp causal law, and a continuous function. Then is non-empty and closed.
The analogue of a learnable class of environments is a learnable class of causal laws.
Definition: Non-anytime learnable class of infra-Bayesian hypotheses
Let denote an indexing set. A class of crisp causal laws (hypotheses) is non-anytime learnable if there exists a set of policies such that for all In this case, we say that learns
Furthermore, we have the analogue of a non-anytime learnable prior over environments.
Definition: Non-anytime learnable prior over crisp causal laws
A prior over a set of causal laws is non-anytime learnable if there exists a set of policies such thatIn this case, we say that learns
Proposition 2 of the preceding post states the classical result from learning theory that if a countable class of environments is learnable, given a non-dogmatic prior over the class, then any family of policies that is Bayes-optimal with respect to the prior must also learn the class. We end with the following corresponding result for crisp causal laws. The proof is contained in the proof section.
Proposition 3: For any non-dogmatic prior over a learnable and countable collection of crisp causal laws , if a family of policies is infra-Bayes optimal with respect to , then learns
Acknowledgements
I'm grateful to Vanessa Kosoy and Alexander Appel for insightful discussions, and Marcus Ogren and Mateusz Bagiński for their valuable feedback on the initial draft.
- ^
In the original infra-Bayesianism sequence, credal sets are called crisp infradistributions.
- ^
First called "unmeasurable uncertainty" by economist Frank Knight in his 1921 book Risk, Uncertainty, and Profit.
- ^
As defined in The Many Faces of Infra-Belief.
- ^
This requires dealing with infinite action spaces, which is typically not a problem as long as the action space is compact Polish.
- ^
Previously called belief functions, e.g. as in The Many Faces of Infra-Belief.
- ^
If using reward rather than loss, this rule can be equivalently formulated as a maximin rule (c.f. Infra-Bayesianism Distillation: Realizability and Decision Theory).
- ^
- ^
- ^
This proposition is a special case of Proposition 5 from Belief Functions And Decision Theory.
- ^
These two statements were written as Proposition 12 in Belief Functions And Decision Theory.