Odds are a tool for expressing relative chances. If the odds of a tree in a forest being sick versus healthy are 2 : 3, this says that there are 2 sick trees for every 3 healthy trees. (The probability of a tree being sick, in this case, is 2/5 or 40%.)
Odds are expressed in the form "X to Y", e.g. "5 to 2". In standard math notation this isThis can also be written as 5:2.
The conceptrepresentation of chances as odds is often used in gambling and statistics and gambling. .
Odds are expressed in the form "X to Y", e.g. "5"7 to 2". This can also be9 for X versus Y", more compactly written as 57:29.
]
Odds are a tool for expressing relative chances. Ifchances. Odds are expressed in the form "X to Y", e.g. "5 to 2". In standard math notation this is written as 5:2. The concept of odds of a treeis often used in a forest being sick versus healthy are 2 : 3, this says that there are 2 sick trees for every 3 healthy trees. (The probability of a tree being sick, in this case, is 2/5 or 40%.)statistics and gambling.
Given n propositions X1,X2,…Xn, a set of odds between the propositions is a list (x1,x2,…,xn) of non-negative real numbers. Each xi in the set of odds is called a "term." Two sets of odds (x1,x2,…,xn) and (y1,y2,…,yn) are called "equivalent" if there is an α>0 such that αxi=yi for all i from 1 to n.
Odds express relative belief: we write "the oddsare a tool for X versus Y are 17:2" when we think that proposition X is 17/2 = 8.5 times as likely as proposition Y.[1]
Odds don't say anything about how likely X or Y is in absolute terms. X might be "it will hail tomorrow" and Y might be "there will be a hurricane tomorrow." In that case, it might be the case that the odds for X versus Y are 17:2, despite the fact that both X and Y are very unlikely. Bayes' rule is an example of an important operation that makes use of expressing relative belief.
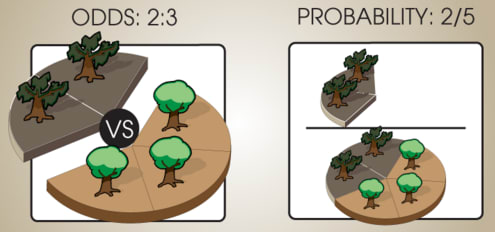
Odds can be expressed between many different propositions at once. For example, let Z be the proposition "It will rain tomorrow," the odds for X vs Y vs Z might be (17:2:100). When odds are expressed between only two propositions, they can be expressed using a single ratio. For example, above, the odds ratio between X and Y is 17/2, the odds ratio between X and Z is 17/100, and the odds ratio between Y and Z is 2/100 = 1/50. This asserts that X is 8.5x more likely than Y, and that Z is 50x more likely than Y. When someone says "the odds ratio of sick to healthy is 2/3", they mean that chances. If the odds of sickness vs healtha tree in a forest being sick versus healthy are 2:3.
Given n propositions X1,X2,…Xn, a set of odds between the propositions is a list (x1,x2,…,xn) of non-negative real numbers. Each xi in the set of odds is called a "term." Two sets of odds (x1,x2,…,xn) and (y1,y2,…,yn) 3, this says that there are called "equivalent" if there is an α>0 such that αxi=yi for all i from 1 to n.
When we write a set of odds using colons, like (x1:x2:…:xn), it is understood that the '=' sign denotes this equivalence. Thus, (3:6)=(9:18).
A set of odds with only two terms can also be written as a fraction xy, where it is understood that xy denotes the odds (x:y). These fractions are often called "odds ratios."
Suppose that in some forest, 40% of the trees are rotten and 60% of the trees are healthy. There are then 2 rottensick trees for every 3 healthy trees, so we say that the relative odds of rotten trees to healthy trees is 2 : 3. If we selected a tree at random from this forest, thetrees. (The probability of getting a rotten tree would bebeing sick, in this case, is 2/5, but the odds would be 2 : 3 for rotten vs. healthy trees.5 or 40%.)
Consider three propositions, X,Y, and Z,...
Coming soon!
We are checking to see if users will click this button, even though we don't have the content for it yet.