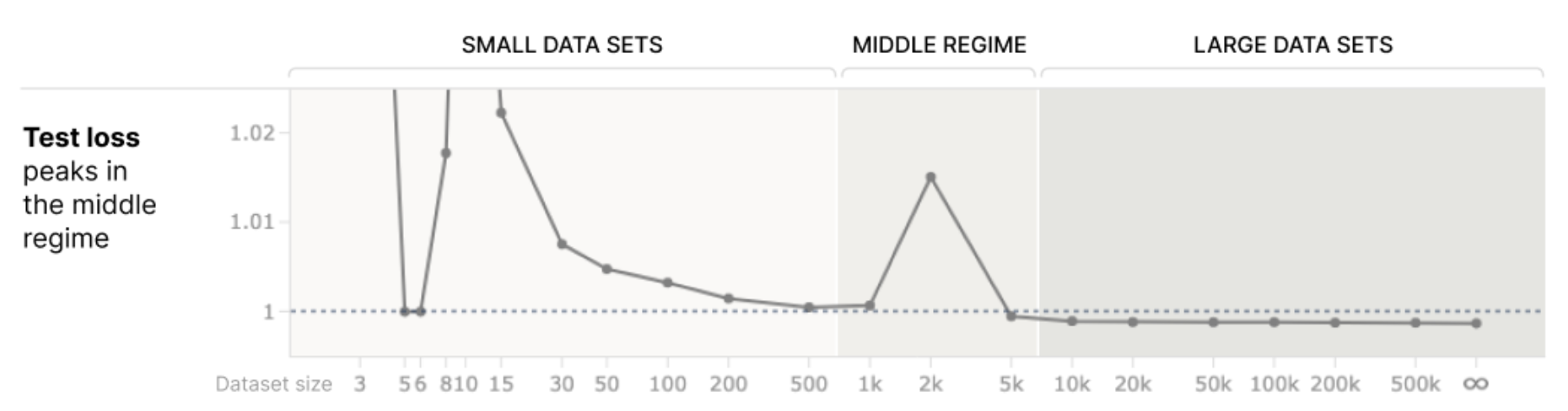
Auditing language models for hidden objectives
We study alignment audits—systematic investigations into whether an AI is pursuing hidden objectives—by training a model with a hidden misaligned objective and asking teams of blinded researchers to investigate it. This paper was a collaboration between the Anthropic Alignment Science and Interpretability teams. Abstract We study the feasibility of conducting...