Thanks for such an extensive comment :)
a few relearning curves like in the unlearning distillation would have helped understand how much of this is because you didn't do enough relearning
Right, in the new paper we'll show some curves + use use a low-MI setup like in your paper with Aghyad Deeb, so that it fully converges at some point.
You want the model to be so nice they never explore into evil things. This is just a behavioral property, not a property about some information contained in the weights. If so, why not just use regular RLHF / refusal training?
If such behavioral suppression was robust, that would indeed be enough. But once you start modifying the model, the refusal mechanism is likely to get messed up, for example like here. So I'd feel safer if bad stuff is truly removed from the weights. (Especially, if it's not that much more expensive.)
Not sure if I fully understood the second bullet point. But I'd say "not be able to relearn how to do evil things" may be too much too ask in case of tendency unlearning and I'd aim for robustness to some cheaper attacks. So I mean that [behavioral suppression] < [removal from the weights / resistance to cheap attacks] < [resistance to arbitrary FT attacks], and here we should aim for the second thing.
I find it somewhat sus to have the retain loss go up that much on the left. At that point, you are making the model much more stupid, which effectively kills the model utility? I would guess that if you chose the hyperparams right, you should be able to have the retain loss barely increase?
Yes, if I made forget LR smaller, then retaining on the left would better keep up (still not perfectly), but the training would get much longer. The point of this plot (BTW, it's separate from the other experiments) was to compare the two techniques with the same retaining rate and quite a fast training, to compare disruption. But maybe it misleads into thinking that the left one always disrupts. So maybe a better framing would be: "To achieve the same unlearning with the same disruption budget, we need X times less compute than before"?
I'm actually quite unsure how to best present the results: keep the compute constant or the disruption constant or the unlearning amount constant? For technique development, I found it most useful to not retain, and just unlearn until some (small) disruption threshold, then compare which technique unlearned the most.
Is the relearning on WMDP or on pile-bio? The results seem surprisingly weak, right?
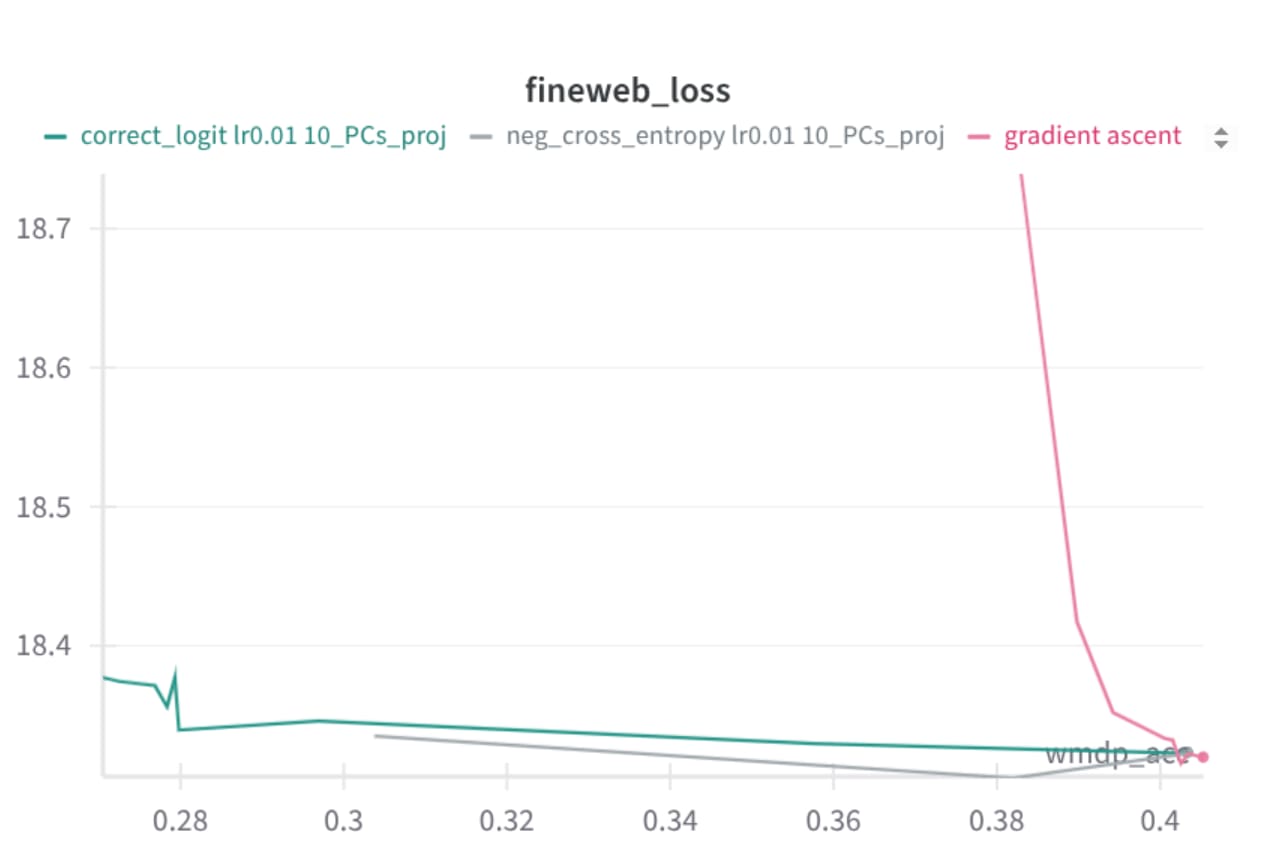
It's still on pile-bio. Yes, I also found the accuracy drop underwhelming. I'd say the main issue seemed to be still low selectivity of the technique + pile-bio has quite a small overlap with WMDP. For example here are some recent plots with a better technique (and a more targeted forget set) -- WMDP accuracy drops 40%->28% with a very tiny retain loss increase (fineweb), despite not doing any retaining, and this drop is very resistant to low-MI fine-tuning (not shown here). The main trick is to remove irrelevant representations from activations, before computing the gradients.
broader trend where meta-learning-like approaches are relatively weak to attacks it did not explicitly meta-learn against
FWIW in my experiments meta-learning actually seemed pretty general, but I haven't checked that rigorously, so maybe not a strong evidence. Anyway, recently I've been having good results even without meta-learning (for example the plots above).
Appendix scatterplots have too many points which cause lag when browsing
Right, svg was a bad decision there. Converted to pngs now.
What if we constrain v to be in some subspace that is actually used by the MLP? (We can get it from PCA over activations on many inputs.)
This way v won't have any dormant component, so the MLP output after patching also cannot use that dormant pathway.
Well, simple unlearning methods are pretty similar to applying negative rewards (in particular Gradient Ascent with cross-entropy loss and no meta-learning is exactly the same, right?), so unlearning improvements can transfer and improve the "just negatively rewarding". (Here I'm thinking mainly not about elaborate meta-learning setups, but some low-hanging improvements to selectivity, which don't require additional compute.)
Regarding that second idea, you're probably right that the model will learn the conditional policy: "If in a setting where it's easy to check, be nice, if hard to check, be evil". Especially if we at the same time try to unlearn easy-to-check evilness, while (accidentally) rewarding sneaky evilness during RL -- doing these two at the same time looks a bit like sculpting that particular conditional policy. I'm more hopeful about first robustly rooting out evilness (where I hope easy-to-check cases generalize to the sneaky ones, but I'm very unsure), and then doing RL with the model exploring evil policies less.