How are you setting when ? I might be totally misunderstanding something but at - feels like you need to push up towards like 2k to get something reasonable? (and the argument in 1.4 for using clearly doesn't hold here because it's not greater than for this range of values).
Well the substance of the claim is that when a model is calculating lots of things in superposition, these kinds of XORs arise naturally as a result of interference, so one thing to do might be to look at a small algorithmic dataset of some kind where there's a distinct set of features to learn and no reason to learn the XORs and see if you can still probe for them. It'd be interesting to see if there are some conditions under which this is/isn't true, e.g. if needing to learn more features makes the dependence between their calculation higher and the XORs more visible.
Maybe you could also go a bit more mathematical and hand-construct a set of weights which calculates a set of features in superposition so you can totally rule out any model effort being expended on calculating XORs and then see if they're still probe-able.
Another thing you could do is to zero-out or max-ent the neurons/attention heads that are important for calculating the feature, and see if you can still detect an feature. I'm less confident in this because it might be too strong and delete even a 'legitimate' feature or too weak and leave some signal in.
This kind of interference also predicts that the and features should be similar and so the degree of separation/distance from the category boundary should be small. I think you've already shown this to some extent with the PCA stuff though some quantification of the distance to boundary would be interesting. Even if the model was allocating resource to computing these XORs you'd still probably expect them to be much less salient though so not sure if this gives much evidence either way.
My hypothesis about what's going on here, apologies if it's already ruled out, is that we should not think of it separately computing the XOR of A and B, but rather that features A and B are computed slightly differently when the other feature is off or on. In a high dimensional space, if the vector and the vector are slightly different, then as long as this difference is systematic, this should be sufficient to successfully probe for .
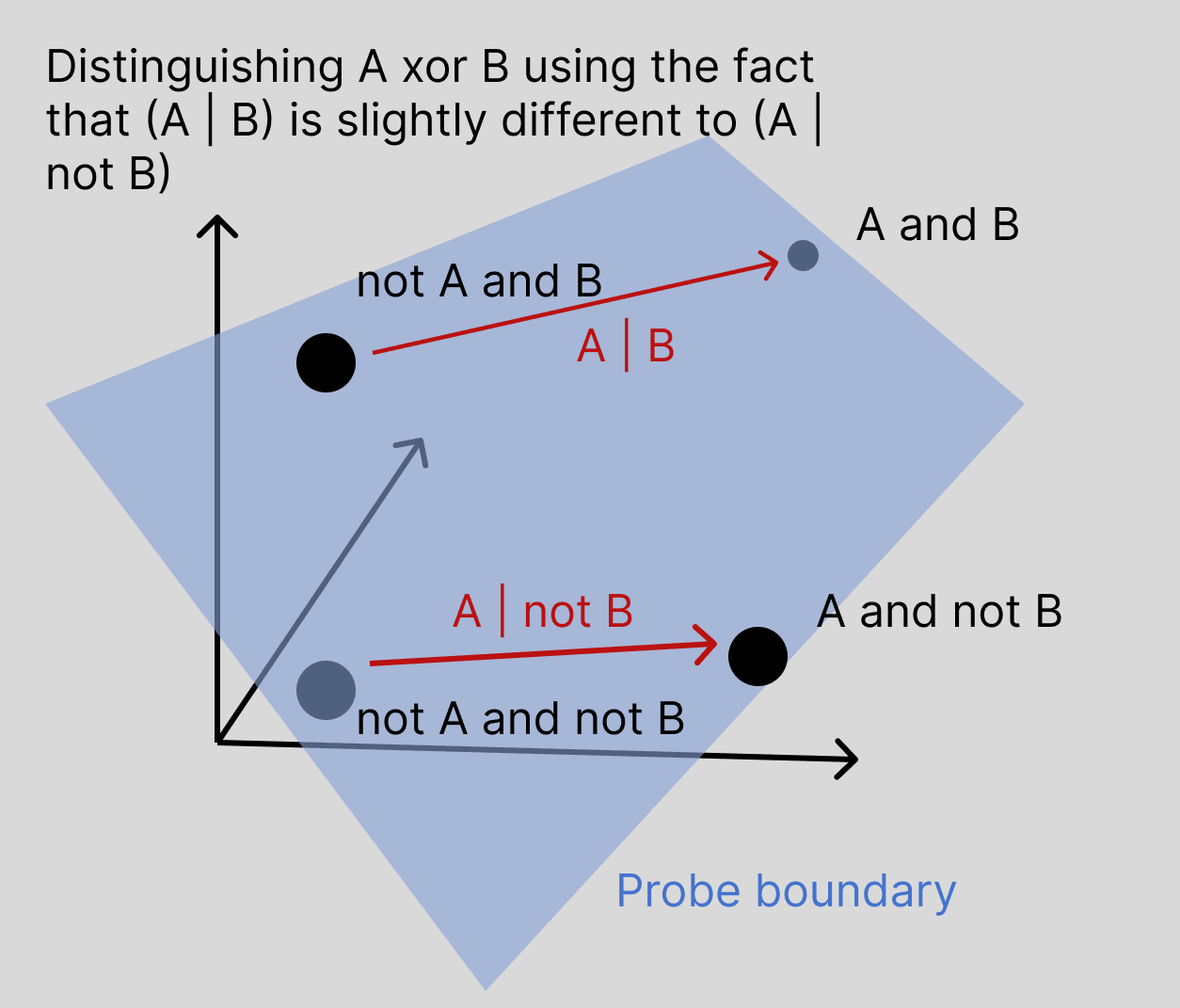
For example, if A and B each rely on a sizeable number of different attention heads to pull the information over, they will have some attention heads which participate in both of them, and they would 'compete' in the softmax, where if head C is used in both writing features A and B, it will contribute less to writing feature A if it is also being used to pull across feature B, and so the representation of A will be systematically different depending on the presence of B.
It's harder to draw the exact picture for MLPs but I think similar interdependencies can occur there though I don't have an exact picture of how, interested to discuss and can try and sketch it out if people are curious. Probably would be like, neurons will participate in both, neurons which participate in A and B will be more saturated if B is active than if B is not active, so the output representation of A will be somewhat dependent on B.
More generally, I expect the computation of features to be 'good enough' but still messy and somewhat dependent on which other features are present because this kludginess allows them to pack more computation into the same number of layers than if the features were computed totally independently.
Could you elaborate on what it would mean to demonstrate 'savannah-to-boardroom' transfer? Our architecture was selected for in the wilds of nature, not our training data. To me it seems that when we use an architecture designed for language translation for understanding images we've demonstrated a similar degree of transfer.
I agree that we're not yet there on sample efficient learning in new domains (which I think is more what you're pointing at) but I'd like to be clearer on what benchmarks would show this. For example, how well GPT-4 can integrate a new domain of knowledge from (potentially multiple epochs of training on) a single textbook seems a much better test and something that I genuinely don't know the answer to.
Do you know why 4x was picked? I understand that doing evals properly is a pretty substantial effort, but once we get up to gigantic sizes and proto-AGIs it seems like it could hide a lot. If there was a model sitting in training with 3x the train-compute of GPT4 I'd be very keen to know what it could do!
Hi Scott, thanks for this!
Yes I did do a fair bit of literature searching (though maybe not enough tbf) but very focused on sparse coding and approaches to learning decompositions of model activation spaces rather than approaches to learning models which are monosemantic by default which I've never had much confidence in, and it seems that there's not a huge amount beyond Yun et al's work, at least as far as I've seen.
Still though, I've not seen almost any of these which suggests a big hole in my knowledge, and in the paper I'll go through and add a lot more background to attempts to make more interpretable models.
Hi Charlie, yep it's in the paper - but I should say that we did not find a working CUDA-compatible version and used the scikit version you mention. This meant that the data volumes used are somewhat limited - still on the order of a million examples but 10-50x less than went into the autoencoders.
It's not clear whether the extra data would provide much signal since it can't learn an overcomplete basis and so has no way of learning rare features but it might be able to outperform our ICA baseline presented here, so if you wanted to give someone a project of making that available, I'd be interested to see it!
Try decomposing the residual stream activations over a batch of inputs somehow (e.g. PCA). Using the principal directions as activation addition directions, do they seem to capture something meaningful?
It's not PCA but we've been using sparse coding to find important directions in activation space (see original sparse coding post, quantitative results, qualitative results).
We've found that they're on average more interpretable than neurons and I understand that @Logan Riggs and Julie Steele have found some effect using them as directions for activation patching, e.g. using a "this direction activates on curse words" direction to make text more aggressive. If people are interested in exploring this further let me know, say hi at our EleutherAI channel or check out the repo :)
For the avoidance of doubt, this accounting should recursively aggregate transitive inputs.
What does this mean?
Super interesting! Have you checked whether the average of N SAE features looks different to an SAE feature? Seems possible they live in an interesting subspace without the particular direction being meaningful.
Also really curious what the scaling factors are for computing these values are, in terms of the size of the dense vector and the overall model?