One framing that I think might be helpful for thinking about "Plan A" vs "shut it all down" is: "Suppose that you have the political will for an n-year slowdown, i.e. after n years, you are forced to handoff trust to superhuman AI systems (e.g. for n = 5, 10, 30). What should the capability progression throughout the slowdown be?" This framing forces a focus on the exit condition / plan to do handoff, which I think is an underdiscussed weakness of the "shut it all down" plan. 

I think my gut reaction is that the most important considerations are: (i) there are a lot of useful things you can do with the AIs, so I want more time with the smarter AIs, and (ii) I want to scale through the dangerous capability range slowly and with slack (as opposed to at the end of the slowdown). 

• this makes me think that particularly for a shorter slowdown (e.g. 5 years), you want to go fast at the beginning (e.g. scale to ~max controllable AI over the first year or two), and then elicit lots of work out of those AIs for the rest of the time period.
• A key concern for the above plan is that govts/labs botch the measurement of "max controllable AI", and scale too far.
• But it's not clear to me how a further delay helps with this, unless you have a plan for making the institutions better over time, or pursuing a less risky path (e.g. ignoring ML and doing human intelligence augmentation).
• Going slower, on the other hand, definitely does help, but requires not shutting it all down.
• More generally, it seems good to do something like "extend takeoff evenly by a factor of n", as opposed to something like "pause for n-1 years, and then do a 1 year takeoff".  
• I am sympathetic to shut all down and go for human augmentation: I do think this reduces AI takeover risk a lot, but this requires a very long pause, and it requires our institutions to bet big on a very unpopular technology. I think that convincing governments to "shut it all down" without an exit strategy at all seems quite difficult as well. 

Ofc this framing also ignores some important considerations, e.g. choices about the capability progression effect both difficulty of enforcement/verification (in both directions: AI lie detectors/ai verification is helpful, while making AIs closer to the edge is a downside), as well as willingness to pay over time (e.g. scary demos or AI for epistemics might help increase WTP) 

One upside of shut it all down is that it does in fact buy more time: in Plan A it is difficult to secure algorithmic secrets without extremely aggressive security measures, hence any rogue projects (e.g. nation state blacksites) can just coast off the algos developed by the verified projects. Then, a few years in, they fire up their cluster and try to do an intelligence explosion with the extra algorithmic progress. 

Yeah, actual FLOPs are the baseline thing that's used in the EO. But the OpenAI/GDM/Anthropic RSPs all reference effective FLOPs. 

If there's a large algorithmic improvement you might have a large gap in capability between two models with the same FLOP, which is not desirable.  Ideal thresholds in regulation / scaling policies are as tightly tied as possible to the risks. 

Another downside that FLOPs / E-FLOPs share is that it's unpredictable what capabilities a 1e26 or 1e28 FLOPs model will have.  And it's unclear what capabilities will emerge from a small bit of scaling: it's possible that within a 4x flop scaling you get high capabilities that had not appeared at all in the smaller model. 

Credit: Mainly inspired by talking with Eli Lifland. Eli has a potentially-published-soon document here.  

The basic case against against Effective-FLOP. 

1. We're seeing many capabilities emerge from scaling AI models, and this makes compute (measured by FLOPs utilized) a natural unit for thresholding model capabilities. But compute is not a perfect proxy for capability because of algorithmic differences. Algorithmic progress can enable more performance out of a given amount of compute. This makes the idea of effective FLOP tempting: add a multiplier to account for algorithmic progress. 
2. But doing this multiplications seems importantly quite ambiguous. 
   1. Effective FLOPs depend on the underlying benchmark. It’s not at all apparent which benchmark people are talking about, but this isn’t obvious. 
      1. People often use perplexity, but applying post training enhancements like scaffolding or chain of thought doesn’t improve perplexity but does improve downstream task performance. 
      2. See https://arxiv.org/pdf/2312.07413 for examples of algorithmic changes that cause variable performance gains based on the benchmark. 
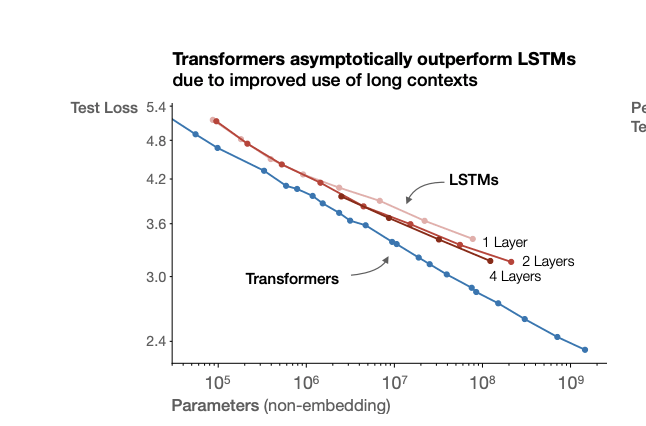
   2. Effective FLOPs often depend on the scale of the model you are testing. See graph below from: https://arxiv.org/pdf/2001.08361 - the compute efficiency from from LSTMs to transformers is not invariant to scale. This means that you can’t just say that the jump from X to Y is a factor of Z improvement on Capability per FLOP.  This leads to all sorts of unintuitive properties of effective FLOPs. For example, if you are using 2016-next-token-validation-E-FLOPs, and LSTM scaling becomes flat on the benchmark, you could easily imagine that at very large scales you could get a 1Mx E-FLOP improvement from switching to transformers, even if the actual capability difference is small. 
   3. If we move away from pretrained LLMs, I think E-FLOPs become even harder to define, e.g., if we’re able to build systems may be better at reasoning but worse at knowledge retrieval. E-FLOPs does not seem very adaptable. 
   4. (these lines would need to parallel for the compute efficiency ratio to be scale invariant on test loss) 
   5. 
3. Users of E-FLOP often don’t specify the time, scale, or benchmark that they are talking about it with respect to, which makes it very confusing. In particular, this concept has picked up lots of steam and is used in the frontier lab scaling policies, but is not clearly defined in any of the documents. 
   1. Anthropic: “Effective Compute: We define effective compute as roughly the amount of compute it would have taken to train a model if no improvements to pretraining or fine-tuning techniques are included. This is operationalized by tracking the scaling of model capabilities (e.g. cross-entropy loss on a test set).”
      1. This specifies the metric, but doesn’t clearly specify any of (a) the techniques that count as the baseline, (b) the scale of the model where one is measuring E-FLOP with respect to, or (c) how they handle post training enhancements that don’t improve log loss but do dramatically improve downstream task capability. 
   2. OpenAI on when they will run their evals: “This would include whenever there is a >2x effective compute increase or major algorithmic breakthrough"
      1. They don’t define effective compute at all. 
   3. Since there is significant ambiguity in the concept, it seems good to clarify what it even means. 
4. Basically, I think that E-FLOPs are confusing, and most of the time when we want to use flops, we’re usually just going to be better off talking directly about benchmark scores. For example, instead of saying “every 2x effective FLOP” say “every 5% performance increase on [simple benchmark to run like MMLU, GAIA, GPQA, etc] we’re going to run [more thorough evaluations, e.g. the ASL-3 evaluations]. I think this is much clearer, much less likely to have weird behavior, and is much more robust to changes in model design. 
   1. It’s not very costly to run the simple benchmarks,  but there is a small cost here. 
   2. A real concern is that it is easier to game benchmarks than FLOPs. But I’m concerned that you could get benchmark gaming just the same with E-FLOPs because E-FLOPs are benchmark dependent — you could make your model perform poorly on the relevant benchmark and then claim that you didn’t scale E-FLOPs at all, even if you clearly have a broadly more capable model. 

A3 in https://blog.heim.xyz/training-compute-thresholds/ also discusses limitations of effective FLOPs. 

Agree with both aogara and Eli's comment. 

One caveat would be that papers probably don’t have full explanations of the x-risk motivation or applications of the work, but that’s reading between the lines that AI safety people should be able to do themselves.

For me this reading between the lines is hard: I spent ~2 hours reading academic papers/websites yesterday and while I could quite quickly summarize the work itself, it was quite hard to me to figure out the motivations.

my current best guess is that gradient descent is going to want to make our models deceptive

Can you quantify your credence in this claim? 

Also, how much optimization pressure do you think that we will need to make models not deceptive? More specifically, how would your credence in the above change if we trained with a system that exerted 2x, 4x, ... optimization pressure against deception? 

If you don't like these or want a more specific operationalization of this question, I'm happy with whatever you think is likely or filling out more details. 

Thanks you for this thoughtful response, I didn't know about most of these projects. I've linked this comment in the DeepMind section, as well as done some modifications for both clarity and including a bit more.  

I think you can talk about the agendas of specific people on the DeepMind safety teams but there isn't really one "unified agenda".

This is useful to know.

There is also the ontology identification problem. The two biggest things are: we don't know how to specify exactly what a diamond is because we don't know the true base level ontology of the universe. We also don't know how diamonds will be represented in the AI's model of the world. 

I personally don't expect coding a diamond maximizing AGI to be hard, because I think that diamonds is a sufficiently natural concept that doing normal gradient descent will extrapolate in the desired way, without inner alignment failures. If the agent discovers more basic physics, e.g. quarks that exist below the molecular level, "diamond" will probably still be a pretty natural concept, just like how "apple" didn't stop being a useful concept after shifting from newtonian mechanics to QM. 

Of course, concepts such as human values/corrigibility/whatever are a lot more fragile than diamonds, so this  doesn't seem helpful for alignment. 

Thanks for your response! I'm not sure I communicated what I meant well, so let me be a bit more concrete. Suppose our loss is parabolic $L:R^3\to R$, where $L\left(x\right)=x_1^2+x_2^2$.  This is like a 2d parabola (but it's convex hull / volume below a certain threshold is 3D). In 4D space, which is where the graph of this function lives and hence where I believe we are talking about basin volume, this has 0 volume. The hessian is the matrix: 

This is conveniently already diagonal, and the 0 eigenvalue comes from the component $x_3$, which is being ignored. My approach is to remove the 0-eigenspace, so we are working just in the subspace where the eigenvalues are positive, so we are left with just the matrix: $\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$, after which we can apply the formula given in the post:

If this determinant was 0 then dividing by 0 would get the spurious infinity (this is what you are talking about, right?). But if we remove the 0-eigenspace we are left with positive volume, and hence avoid this division by 0. 

I am a bit confused how you deal with the problem of 0 eigenvalues in the Hessian. It seems like the reason that these 0 eigenvalues exist is because the basin volume is 0 as a subset of parameter space. My understanding right now of your fix is that you are adding $\lambda +c$ along the diagonal to make the matrix full rank (and this quantity is coming from the regularization plus a small quantity). Geometrically, this seems like drawing a narrow ellipse around the subspace of which we are trying to estimate the volume. 

But this doesn't seem natural to me, seems to me like the most important part of determining volume of these basins is the relative dimensionality. If there are two loss basins, but one has dimension greater than the other, the larger one dominates and becomes a lot more likely. If this is correct, we only care about the volume of basins that have the same number of dimensions. Thus, we can discard the dimensions with 0 eigenvalue and just apply the formula for the volume over the non-zero eigenvalues (but only for the basins with maximum rank hessians). This lets us directly compare the volume of these basins, and then treat the low dimensional basins as having 0 volume. 

Does this make any sense?