I’ve encountered various claims about how AIs would approach game theory and decision theory that seem pretty importantly mistaken. Some of these confusions probably aren’t that big a deal on their own, and I’m definitely not the first to point out several of these, even publicly. But collectively I think these add up to a common worldview that underestimates the value of technical work to reduce risks of AGI conflict. I expect that smart agents will likely avoid catastrophic conflict overall—it’s just that the specific arguments for expecting this that I’m responding to here aren’t compelling (and seem overconfident).
For each section, I include in the footnotes some examples of the claims I’m pushing back on (or note whether I’ve primarily seen these claims in personal communication). This is not to call out those particular authors; in each case, they’re saying something that seems to be a relatively common meme in this community.
Summary:
- The fact that conflict is costly for all the agents involved in the conflict, ex post, doesn’t itself imply AGIs won’t end up in conflict. Under their uncertainty about each other, agents with sufficiently extreme preferences or priors might find the risk of conflict worth it ex ante. (more)
- Solutions to collective action problems, where agents agree on a Pareto-optimal outcome they’d take if they coordinated to do so, don’t necessarily solve bargaining problems, where agents may insist on different Pareto-optimal outcomes. (more)
- We don’t have strong reasons to expect AGIs to converge on sufficiently similar decision procedures for bargaining, such that they coordinate on fair demands despite committing under uncertainty. Existing proposals for mitigating conflict given incompatible demands, while promising, face some problems with incentives and commitment credibility. (more)
- The commitment races problem is not just about AIs making commitments that fail to account for basic contingencies. Updatelessness (or conditional commitments generally) seems to solve the latter, but it doesn’t remove agents’ incentives to limit how much their decisions depend on each other’s decisions (leading to incompatible demands). (more)
- AIs don’t need to follow acausal decision theories in order to (causally) cooperate via conditioning on each other’s source code. (more)
- Most supposed examples of Newcomblike problems in everyday life don’t seem to actually be Newcomblike, once we account for “screening off” by certain information, per the Tickle Defense. (more)
- The fact that following acausal decision theories maximizes expected utility with respect to conditional probabilities, or counterfactuals with the possibility of logical causation, doesn’t imply that agents with acausal decision theories are selected for (e.g., acquire more material resources). (more)
Ex post optimal =/= ex ante optimal[1]
An “ex post optimal” strategy is one that in fact makes an agent better off than the alternatives, while an “ex ante optimal” strategy is optimal with respect to the agent’s uncertainty at the time they choose that strategy. The idea that very smart AGIs could get into conflicts seems intuitively implausible because conflict is, by definition, ex post Pareto-suboptimal. (See the “inefficiency puzzle of war.”)
But it doesn’t follow that the best strategies available to AGIs given their uncertainty about each other will always be ex post Pareto-optimal. This may sound obvious, but my experience with seeing people’s reactions to the problem of AGI conflict suggests that many of them haven’t accounted for this important distinction.
As this post discusses in more detail, there are two fundamental sources of uncertainty (or acting as if uncertain) AGIs might have about each other when they choose bargaining strategies:
- Private information: Instead of fighting, we could agree to a deal where each side gets a fraction of the pie proportional to their probability of winning the fight (a “mock fight” deal). But I might think you’re bluffing about how likely you are to win, and not have a way to objectively verify this probability.[2] More on obstacles to apparent solutions to this problem here.
- Commitment under uncertainty about the other’s commitment (or, “updatelessness”): The mock fight deal is one possible Pareto improvement on the conflict default. But it’s not the only one—if fighting is sufficiently costly,[3] each of us can say, “We’re both better off than the default if I get the whole pie!”
How do we decide between these? In the True Prisoner’s Dilemma (or rather, as discussed in the next section, True Chicken), there’s no “we.” If I’m an amoral alien, you really don’t want to compromise with me if you can get away with it. You might therefore commit to demand epsilon less than the whole pie, or else you’ll fight, and “race” to do so in a way that is not influenced by my decision. And I might demand more than epsilon. If I went along with your demand for the sake of peace, I’d be an exploitable sucker!
Each of us is incentivized to choose our demand without knowing what exactly the other will demand, because if you wait to eliminate your uncertainty before making a demand, you lose the opportunity to influence the bargain with your commitment. (See below for why, e.g., Yudkowsky’s “meta-bargaining” proposal isn’t sufficient to resolve this.)
Is this risky? Absolutely. I definitely don’t expect hawkish demands to be the norm, because they’re generally riskier than fair demands—which are accepted by a wider range of agents than unfair demands, due to being symmetric in some sense. Evolution tends to select for intrinsic preferences for symmetric notions of fairness. But mindspace is large. We can’t be so confident that AGIs with different values from us will find the risks of conflict greater than the ex ante gains from exploiting others.[4]
Cooperation =/= pure coordination / collective action / defeating Moloch[5]
I think when many people hear about “cooperation” problems faced by AGIs, they imagine Prisoner’s Dilemmas (or Stag Hunts). I.e., they imagine that the problem is that all the actors involved agree on a Pareto-optimal outcome they’d like to move towards, but because of strict dominance (or risk dominance) arguments, they fail to coordinate on that outcome.
We know how to solve those: You conditionally commit to aim for the agreed Pareto-optimal outcome (e.g., Cooperate in the Prisoner’s Dilemma) if and only if the other players also do so. This is well-studied in the “program equilibrium” literature. (More on this later.) And it’s plausible that AGIs will be able to credibly implement these kinds of conditional commitments.[6]
But cooperation problems encompass more than these collective action problems. I’m more concerned about bargaining problems, illustrated by (2) in the previous section: The AGIs might not agree on which Pareto-optimal outcome to aim for,[7] and resort to dangerous commitment race-y tactics to jockey for their preferred outcomes.[8] Chicken and the Ultimatum Game are prototypical examples.
The basic distinction here:
- Collective action problems are problems posed by nature. The AGIs agree on some preferred alternative outcome, and just need to leverage their increasing capabilities to implement technologies that bring them to that outcome.
- Bargaining problems are problems posed by other AGIs. There’s no obvious guarantee that increasing capabilities dissolve such problems. (The closest candidate I’m aware of is Oesterheld and Conitzer’s safe Pareto improvements, but that’s not a slam dunk either for reasons beyond the scope of this post.)
(Some nice exceptions acknowledging this distinction are Wentworth here and Demski here.)
You aren’t guaranteed to determine the other agent’s response[9]
(I think the following is the most important misconception in this list, weighted by how common it is.)
A common reaction to the bargaining and commitment races problems is: “Just commit to a fair demand, and reject unfair demands in proportion to how unfair they are.” Call this the Fair Policy.
Suppose that conditional on each agent demanding a bargaining solution that’s symmetric, they coordinate on the same solution. Even so, in order for this proposal to “solve” bargaining, as far as I can tell one of the following assumptions is required, none of which I find plausible:
- “Virtually all[10] agents who are sufficiently capable to enter high-stakes bargaining interactions will coordinate on the Fair Policy.” If, as in a commitment race, the agents face competitive pressures to commit before communicating with each other, it seems that this assumption would in turn require:
- “Virtually all agents who are sufficiently capable to enter high-stakes bargaining interactions will converge on the same decision procedure, and reason that their decision to use the Fair Policy logically causes[11] their counterparts to do likewise.”[12] For many kinds of problems, I think it’s reasonable to expect convergence between arbitrarily capable agents’ methods of reasoning about those problems, namely, to the most effective methods. But:
- Agents need not be arbitrarily capable when they need to make high-stakes bargaining decisions (especially given commitment races).
- If the reason to expect convergence of decision procedures in bargaining problems is that we expect selection for the same decision theory, then: First, see below for reasons to doubt such selection pressures exist.[13] Second, merely sharing the same decision theory that you consult as an ideal doesn’t mean you’ll share a whole decision procedure (with respect to the given problem). For example, you might not share how you model the decision problem, what kinds of evidence about other agents are most salient to you, how you approximate ideal Bayesianism, etc.[14]
- We might think that agents converge on the same decision procedure with respect to bargaining, not just the same decision theory as their ideal, because there’s one such procedure that’s more effective than others. As noted above, bargaining problems are posed by other agents—so, to speak of “more effective” methods of reasoning about bargaining, we need to specify a distribution of counterparts. So, if either the distribution of agents a given AGI encounters over its history of lower-stakes interactions is sensitive to the initial agents, or AGIs have different priors about potential counterparts, it’s plausible that different highly capable agents will be selected on different distributions of other agents. Therefore they might have different bargaining decision procedures, which weakens the logical dependence between their decisions.
- “Virtually all agents who are sufficiently capable to enter high-stakes bargaining interactions will converge on the same decision procedure, and reason that their decision to use the Fair Policy logically causes[11] their counterparts to do likewise.”[12] For many kinds of problems, I think it’s reasonable to expect convergence between arbitrarily capable agents’ methods of reasoning about those problems, namely, to the most effective methods. But:
- “If you use the Fair Policy, your counterpart will choose their policy as a function of yours—in particular, they’ll best-respond.” Why should you be confident they’ll do that? After all, you aren’t choosing your policy as a function of theirs, because you don’t want to get exploited. You shouldn’t be extremely confident they won’t follow similar logic.
- To clarify, I’m not saying agents should reason as if their counterparts will always follow the same reasoning. Precisely the opposite: The “just commit to a fair demand” proposal only solves the whole problem when everyone else does the same thing. And we saw above some reasons to be skeptical that AIs will blindly coordinate in that way.
- Rather, the danger is other agents following similar logic insofar as they avoid conditioning their policy on yours. I.e., they may reason that many agents will comply with their demands as long as such demands are unconditional, and therefore unconditionally demand more for themselves.
This is related to why another proposal to avoid conflict in bargaining isn’t a full solution. Consider Yudkowsky’s idea in this post:
The way this might work is that you pick a series of increasingly unfair-to-you, increasingly worse-for-the-other-player outcomes whose first element is what you deem the fair Pareto outcome: (100, 100), (98, 99), (96, 98). Perhaps stop well short of Nash if the skew becomes too extreme. Drop to Nash as the last resort. The other agent does the same, starting with their own ideal of fairness on the Pareto boundary. Unless one of you has a completely skewed idea of fairness, you should be able to meet somewhere in the middle. Both of you will do worse against a fixed opponent's strategy by unilaterally adopting more self-favoring ideas of fairness. Both of you will do worse in expectation against potentially exploitive opponents by unilaterally adopting looser ideas of fairness.
In other words, suppose that instead of defaulting to fighting you if you reject my offer, I make a counteroffer that is worse for me and very slightly worse for you,[15] and repeat. If you do the same, we’ll eventually meet at a bargain that, while not Pareto-efficient, is still better than conflict.
Conditional on us agreeing to this procedure, it’s true that we avoid conflict without giving each other perverse incentives—if I make a larger demand, by construction this doesn’t make me better off. That’s a nice pair of properties!
But consider an aligned AI “Friendly” and misaligned AI “Clippy.” Clippy is very confident that without this procedure, Friendly will back down without a fight, and conflict isn’t so costly by Clippy’s lights anyway. (I suspect Clippy shouldn’t be so confident in this, but that requires an independent argument.) Before Friendly credibly commits to their own demand, Clippy reasons, “If I agree to this procedure, Friendly will know we’ll avoid the particularly costly conflict. So they’ll want to make a more aggressive demand than they would have if I had opted out.” Clippy therefore opts out.
Naturally, a potential solution is for Friendly to commit to not make a more aggressive demand if Clippy participates than if Clippy opts out. But this commitment needs to be made sufficiently credible. That might be relatively challenging compared to verifying other kinds of commitments, because it needs to be verified that Friendly would have behaved in a certain way (after some timeframe where various inputs might have entered into Friendly’s decision-making) given counterfactual beliefs. And whether this works also depends on some nontrivial assumptions on how Friendly updates on Clippy’s (non-)participation.[16]
It’s also worth recalling that AGIs need not be arbitrarily capable at bargaining in order to attain enough power to get into high-stakes bargaining problems. So we can’t be highly confident that AGIs will implement solutions to the problems above by default—especially if doing so requires time-sensitive measures to establish the credibility of their cooperative commitments, under other strategic pressures in a multipolar takeoff.
Updatelessness doesn’t solve commitment races[17]
Another somewhat common claim is, “Agents don’t really need to commit to anything for strategic purposes. If you’re (open-mindedly) updateless, you can just decide to do that which a wiser version of your past self would have wanted to commit to, without updating on information that would reduce your bargaining power.”
Assume that an agent can act according to an updateless procedure at the time when they face a critical bargaining decision, and can make their updatelessness credible to other agents. I think these are big assumptions,[18] but at any rate: If these assumptions hold, something like the above argument might indeed dispel worries that agents will make commitments that are ex ante “dumb,” i.e., fail to account for useful information / reflection that in fact wouldn’t have reduced their bargaining power. For example, if the reason you commit to a bargaining policy that conflicts with others’ is literally just that you didn’t consider some other impartial bargaining solution, open-minded updatelessness saves you.
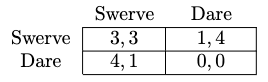
That is not the kind of commitment race that I think is a fundamental problem. In the case of two updateless agents, the problem is that when both of them avoid conditioning on information that would reduce their bargaining power—i.e., knowledge of each other’s demands—they are basically back to playing a game of simultaneous Chicken (figure below). In which case, they each have incentives to Dare to the extent that they ex ante expect each other to Swerve. And they aren’t guaranteed to have identical priors from which they compute the ex ante optimal decision. (Demski writes a similar point here.)
Acausal decision theories are not necessary for program equilibrium / Löbian cooperation[19]
Causal decision theorists don’t always defect in the one-shot Prisoner’s Dilemma. Yes, if you drop a CDT agent into a one-shot Prisoner’s Dilemma de novo, and they only have access to the unconditional Cooperate and Defect strategies, they will defect. But many if not most real-world Prisoner’s Dilemmas are not like this, especially for advanced AGIs.
The CDT agent can use a conditional commitment, like McAfee’s classic, “If other player’s code == my code: Cooperate; else: Defect.” If that’s too brittle for your liking, you can use conditional commitments that verify cooperation via provability logic, or the recursive “robust program equilibrium” method. In a causal interaction with another agent, none of this requires an acausal decision theory: Programs can implement conditional commitments and read each other, causally.
Newcomblike problems aren’t the norm[20]
I think people have overstated the frequency of Newcomblike problems—roughly, cases that distinguish causal from acausal decision theories—“in the wild.” (Note that I wouldn’t count something as a “Newcomblike problem” if the non-causal dependence between one’s action and payoff is too weak to be action-guiding, even if it’s nonzero.)
Soares argues that Newcomblike problems are ubiquitous because, in social interactions, we “leak information about how we make decisions” on which others base their decisions. I’m unconvinced his examples are truly Newcomblike, however:
- Example 1: How trustworthy you are determines both your own decision, and your microexpressions that shape the other person’s decision (based on how trustworthy they find you).
- Any purported correlations between your decision and your microexpressions, mediated via trustworthiness as a common cause, should be conditioned on what you know about 1) your own trustworthiness, and 2) how you’re reasoning about your microexpressions (and their effects on others’ responses). Just because an antisocial action is unconditionally correlated with information about the actor’s trustworthiness, it doesn’t follow that when you’re thinking about the implications of your action for your trustworthiness, you are less likely to be seen as trustworthy when you do the antisocial action. This is the Tickle Defense.
- It seems that the act of seriously considering the antisocial action is what causes you to make the microexpression that makes others not trust you. (C.f. discussion of the “screening by inclination” version of the Tickle Defense in Ahmed’s Evidence, Decision, and Causality, Ch. 4.)
- Example 2: In games involving deception, like Poker and Diplomacy, you leak information about your strategy via your expressions.
- But managing your own “poker face” is just about causally manipulating your expressions so that you can send signals that profit you.
- Example 3: A job candidate’s demeanor determines both how confidently they act and how positively their interviewer is disposed toward them.
- Soares correctly notes that the candidate should resolve to be bold, because “a person who knows they are going to be bold will have a confident demeanor.” But this just implies that resolving/committing to be bold causally improves the candidate’s job prospects. If the candidate doesn’t resolve to be bold, then when they find themselves acting according to a shy demeanor, they can’t just retroactively cancel this effect by acting bold[21]—per the Tickle Defense, they need to condition the correlation on them choosing to be bold for this acausal decision theory-motivated reason.[22]
- He adds that if a CDT agent commits to being bold, “this would involve using something besides causal counterfactual reasoning during the actual interview.” This is misleading, because committing to being bold restricts the agent’s action space in the interview. So they don’t need to violate CDT when they face the interview. I think a perfectly natural account of the bold job candidate’s success is not that they are having some acausal influence, but that they are using a “fake it 'til you make it” approach, i.e., acting bold initially so as to reinforce their confidence and causally influence both the interviewer and their future behavior.
Why does all this matter? Mainly because claims that acausally motivated decision-making is typical are often used to argue that acausal decision theories systematically succeed in real-world contexts where CDT fails. This brings us to:
There’s no clear objective selection pressure towards acausal decision theories[23]
Finally: as someone who’s very sympathetic to one-boxing in standard Newcomb’s problem, I had to be dragged kicking and screaming into accepting the following point.[24]
Many adherents of acausal decision theories claim that these decision theories “win,” i.e., outperform CDT. If you’re the sort of person who finds intuitive the normative criterion of maximizing expected utility with respect to conditionals, or with respect to counterfactuals that admit some notion of “logical causation,” then sure, it will seem very obvious to you that (the standard form of) CDT “loses.” Why ain’cha rich, David Lewis?[25]
For pumping intuitions about the normative criterion you favor upon reflection, I think this move is sensible.[26] But this doesn’t get us to the empirical claim, “Agents who one-box will systematically outcompete two-boxers in some sense that selects for the former.” That claim seems to require an argument for one of the following:
- “One-boxers will tend to acquire more resources, therefore agents with acausal decision theories will acquire more resources.” I haven’t heard a compelling argument of this form that can’t be debunked by positing that the two-boxers commit to resist some form of exploitation, or to one-box in Newcomblike situations they expect in the future. But such commitments are consistent with the two-boxers’ normative criterion of CDT (as we saw above). (In particular, these commitments don’t require them to follow the prescriptions of an acausal decision theory in contexts where they can’t commit.)[27]
- Related: Soares’s claim that agents who follow logical decision theories (LDT) will profit more than those who don’t, in expectation, by acausally cooperating with each other. I find this unconvincing because if indeed some policy of accepting deals that are ex post worse for you is ex ante optimal, again, a CDT agent could commit to that policy. You might object that the LDT agent doesn’t need to anticipate this situation ahead of time, they can just cooperate on the fly. But either a) Bob commits to LDT ahead of time, in which case this defense is moot, or b) Bob previously didn’t follow LDT and decides now to follow LDT. In the latter case, we need a whole separate argument for why we should think Bob and Alice have such logically entangled decision procedures that their decisions determine each other.[28] As discussed above, it’s not enough that they both try to consult the same “decision theory” on paper.
- Further, some reinforcement learning algorithms evidently select for CDT-like behavior in Newcomblike problems. See, e.g., Garrabrant here and Bell et al. (2021).[29]
- “Generally intelligent reasoning (which will be selected for) leads to endorsement of one-boxing.” But we don’t have objective metrics according to which one-boxing is non-question-beggingly superior.
Acknowledgments
Thanks to Jesse Clifton, Daniel Kokotajlo, Sylvester Kollin, Martín Soto, and Alana Xiang for comments and suggestions.
- ^
- ^
Technically in Bayesian game theory, this is framed as a problem of ex interim uncertainty instead of ex ante. This just means the agent doesn’t decide just based on the common prior, rather, they update on what they know about their own private information.
- ^
This is relevant because it determines whether, e.g., I prefer to gamble on fighting you rather than concede to your demand of the whole pie.
- ^
Given this, I’m not especially excited about work identifying symmetric bargaining solutions (in the technical sense defined here) that may be more attractive Schelling points than preexisting ones, compared to thinking about how to resolve problems posed by incentives not to accept any symmetric bargain.
- ^
Examples:
* Although Yudkowsky doesn’t directly make this mistake in this comment, his argument is (partly) that the existence of a “solution” to the one-shot Prisoner’s Dilemma (a collective action problem) should make us suspect the same for bargaining problems like the Ultimatum Game;
* Various personal communications.
- ^
But see, e.g., this thread.
- ^
Technically, Prisoner’s Dilemmas can be bargaining problems too, when you can use correlated randomization. This is the lesson of the commitment game folk theorem.
- ^
I attempted to convey this point in this comment.
- ^
Examples:
* Yudkowsky in this comment.
* Udell in this post: “Bot will only win in a commitment race with Eliezer if Bot self-modifies for the wrong reason, in advance of understanding why self-modification is valuable. Bot, if successful, acted on mere premonitions in his prior reasoning about self-modification. Bot got to, and could only get to, a winning state in the logical mental game against Eliezer "by accident."”
* Udell’s suggestion here that “precommit[ting] to dividing the value pie according to your notion of fairness” successfully “head[s] off getting into commitment races with each other over splits.”
- ^
I think requiring literally all bargaining problems to be solved is too high a bar.
- ^
See, e.g., logical decision theory—though note that other decision theories can still account for the logical non-causal implications of an agent’s decision.
- ^
(H/t Jesse Clifton for bringing to my attention a steelman of this position; he does not endorse this position.)
- ^
That section discusses the causal vs. acausal decision theory distinction, but the same argument seems to apply to other decision theory axes.
- ^
Kollin writes about a related problem for logical decision theory-based cooperation here.
- ^
Or, as Armstrong proposes in this comment, my counteroffer could be exactly as good for you as the previous offer.
- ^
Some of my current research is on these problems.
- ^
- ^
First: Updateful decision-making seems to work in the vast majority of other decision contexts—similar to my claim below that Newcomblike problems aren’t that common, the same can be said for problems that separate updateful and updateless agents. Given this, for the critical decision in question the agent would need to overcome what seem to be strong default psychological pressures to decide updatefully. (Perhaps this is just easier for AI minds than human minds, for some reason, though.) The agent would also need to retroactively compute the ex ante optimal act. Second, insofar as updateful decision making is the natural default as I claimed, and making commitments to non-default behavior credible is generally challenging, other agents aren’t guaranteed to find the agent’s updatelessness credible.
- ^
Examples:
* From “Introduction to Logical Decision Theory for Computer Scientists” on Arbital: “A truly pure causal decision agent, with no other thoughts but CDT, will wave off all that argument with a sigh; you can't alter what Fairbot2 has already played in the Prisoner's Dilemma and that's that.”
* From Critch (2016): “In this paper, we find that classical game theory—and more generally, causal decision theory (Gibbard and Harper 1978)—is not an adequate framework for describing the competitive interactions of algorithms that reason about the source codes of their opponent algorithms and themselves.” (See also section 6.1.) I think a particularly charitable reading of this is that Critch is claiming that a CDT agent will not reason about how its decisions logically determine its own algorithm, even if they can adopt conditional commitments that do Löbian cooperation. But without more extensive discussion, the claim seems potentially misleading.
- ^
- ^
They can, of course, turn the interview in their favor by changing their behavior, but this can clearly be modeled as causally shaping their future demeanor.
- ^
To be clear, I definitely don’t think the candidate has perfect introspection of the causes of their decision. Rather, it seems plausible that they have strong enough introspection ability to screen off the action-relevant acausal effect here.
- ^
- ^
Thanks to Sylvester Kollin and Jesse Clifton for doing the “dragging” here.
- ^
(h/t Sylvester Kollin) Relatedly, Hintze (2014) argues that updateless decision theory “succeeds” more than others, but this just trivially follows from their definition of success as maximizing ex ante expected utility.
- ^
Though see, e.g., Bales (2018) for what I take to be a contrary view (I’m unsure exactly how much we disagree).
- ^
I would give the same reply to claims that, e.g., UDT outcompetes updateful EDT.
- ^
“Logical decision theorists don’t need to be able to make side-trades to accept such bets, and they’ll keep taking advantage of certain gains even if you forbid such trades. Like, if Alice and Bob have common knowledge that the market is either going to be offered the trade “Alice gains $1,000,000; Bob loses $1” or the trade “Alice loses $1; Bob gains $1,000,000”, with equal probability of each, and they’re not allowed to trade between themselves, then they can (and will, if they’re smart) simply agree to accept whichever trade they’re presented.”
- ^
(h/t Lukas Finnveden and Jesse Clifton)
* Garrabrant: “This problem will, for example, cause a logical inductor EDT agent to defect in a prisoner’s dilemma against a similar power agent that is trying to imitate it. If such an agent were to start out cooperating, random defection will be uncorrelated with the opponent’s prediction. Thus the explored defection will be profitable, and the agent will learn to defect. The opponent will learn this and start predicting defection more and more, but in the long run, the agent view this as independent with its action.”
* Bell et al. (2021) show that under some assumptions, value-based RL can only converge to policies that are ratifiable, which in Newcomb’s problem implies two-boxing.