What counts as defection?
7TurnTrout
6Rohin Shah
4jimmy
3TurnTrout
3ESRogs
2ESRogs
2TurnTrout
3Dagon
1TurnTrout
New Comment
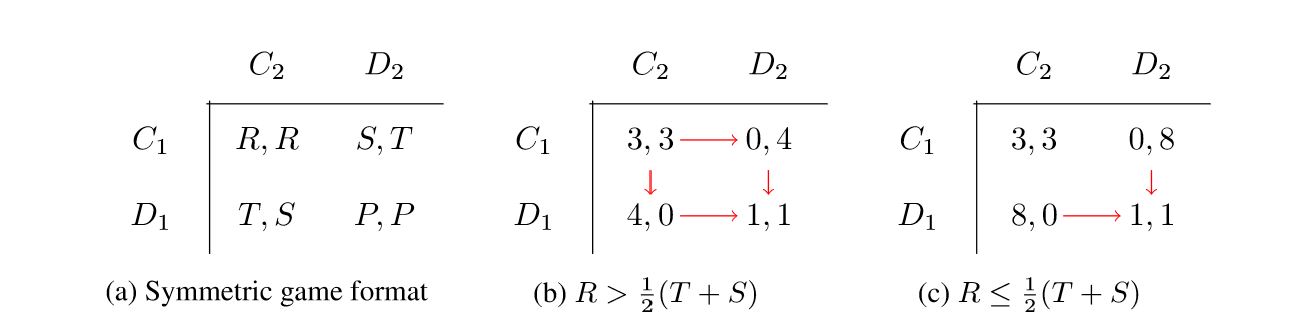
This post's main contribution is the formalization of game-theoretic defection as gaining personal utility at the expense of coalitional utility.
Rereading, the post feels charmingly straightforward and self-contained. The formalization feels obvious in hindsight, but I remember being quite confused about the precise difference between power-seeking and defection—perhaps because popular examples of taking over the world are also defections against the human/AI coalition. I now feel cleanly deconfused about this distinction. And if I was confused about it, I'd bet a lot of other people were, too.
I think this post is valuable as a self-contained formal insight into the nature of defection. If I could vote on it, I'd give it a 4 (or perhaps a 3, if the voting system allowed it).
Planned summary for the Alignment Newsletter:
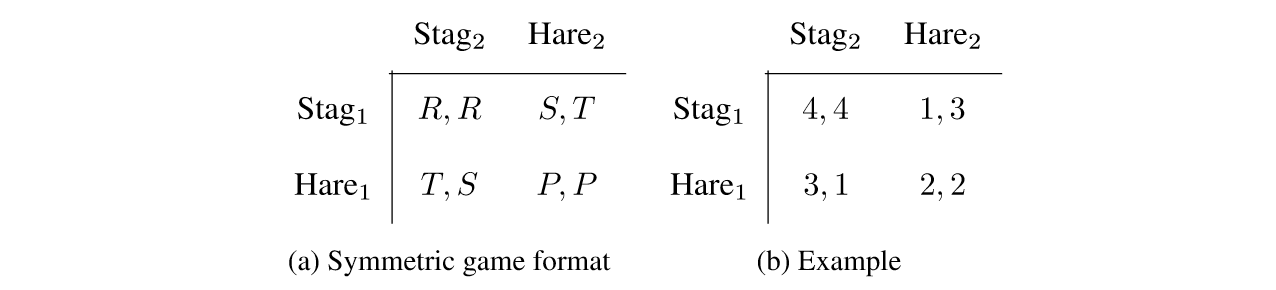
We often talk about cooperating and defecting in general-sum games. This post proposes that we say that a player P has defected against a coalition C (that includes P) currently playing a strategy S when P deviates from the strategy S in a way that increases his or her own personal utility, but decreases the (weighted) average utility of the coalition. It shows that this definition has several nice intuitive properties: it implies that defection cannot exist in common-payoff games, uniformly weighted constant-sum games, or arbitrary games with a Nash equilibrium strategy. A Pareto improvement can also never be defection. It then goes on to show the opportunity for defection can exist in the Prisoner’s dilemma, Stag hunt, and Chicken (whether it exists depends on the specific payoff matrices).
As others have mentioned, there's an interpersonal utility comparison problem. In general, it is hard to determine how to weight utility between people. If I want to trade with you but you're not home, I can leave some amount of potatoes for you and take some amount of your milk. At what ratio of potatoes to milk am I "cooperating" with you, and at what level am I a thieving defector? If there's a market down the street that allows us to trade things for money then it's easy to do these comparisons and do Coasian payments as necessary to coordinate on maximizing the size of the pie. If we're on a deserted island together it's harder. Trying to drive a hard bargain and ask for more milk for my potatoes is a qualitatively different thing when there's no agreed upon metric you can use to say that I'm trying to "take more than I give".
Here is an interesting and hilarious experiment about how people play an iterated asymmetric prisoner's dilemma. The reason it wasn't more pure cooperation is that due to the asymmetry there was a disagreement between the players about what was "fair". AA thought JW should let him hit "D" some fraction of the time to equalize the payouts, and JW thought that "C/C" was the right answer to coordinate towards. If you read their comments, it's clear that AA thinks he's cooperating in the larger game, and that his "D" aren't anti-social at all. He's just trying to get a "fair" price for his potatoes, and he's mistaken about what that is. JW, on the other hand, is explicitly trying use his Ds to coax A into cooperation. This conflict is better understood as a disagreement over where on the Pareto frontier ("at which price") to trade than it is about whether it's better to cooperate with each other or defect.
In real life problems, it's usually not so obvious what options are properly thought of as "C" or "D", and when trying to play "tit for tat with forgiveness" we have to be able to figure out what actually counts as a tit to tat. To do so, we need to look at the extent to which the person is trying to cooperate vs trying to get away with shirking their duty to cooperate. In this case, AA was trying to cooperate, and so if JW could have talked to him and explained why C/C was the right cooperative solution, he might have been able to save the lossy Ds. If AA had just said "I think I can get away with stealing more value by hitting D while he cooperates", no amount of explaining what the right concept of cooperation looks like will fix that, so defecting as punishment is needed.
In general, the way to determine whether someone is "trying to cooperate" vs "trying to defect" is to look at how they see the payoff matrix, and figure out whether they're putting in effort to stay on the Pareto frontier or to go below it. If their choice shows that they are being diligent to give you as much as possible without giving up more themselves, then they may be trying to drive a hard bargain, but at least you can tell that they're trying to bargain. If their chosen move is conspicuously below (their perception of) the Pareto frontier, then you can know that they're either not-even-trying, or they're trying to make it clear that they're willing to harm themselves in order to harm you too.
In games like real life versions of "stag hunt", you don't want to punish people for not going stag hunting when it's obvious that no one else is going either and they're the one expending effort to rally people to coordinate in the first place. But when someone would have been capable of nearly assuring cooperation if they did their part and took an acceptable risk when it looked like it was going to work, then it makes sense to describe them as "defecting" when they're the one that doesn't show up to hunt the stag because they're off chasing rabbits.
"Deliberately sub-Pareto move" I think is a pretty good description of the kind of "defection" that means you're being tatted, and "negligently sub-Pareto" is a good description of the kind of tit to tat.
As others have mentioned, there's an interpersonal utility comparison problem. In general, it is hard to determine how to weight utility between people.
I actually don't think this is a problem for the use case I have in mind. I'm not trying to solve the comparison problem. This work formalizes: "given a utility weighting, what is defection?". I don't make any claim as to what is "fair" / where that weighting should come from. I suppose in the EGTA example, you'd want to make sure eg reward functions are identical.
"Deliberately sub-Pareto move" I think is a pretty good description of the kind of "defection" that means you're being tatted, and "negligently sub-Pareto" is a good description of the kind of tit to tat.
Defection doesn't always have to do with the Pareto frontier - look at PD, for example. , , are usually all Pareto optimal.
Combining the two conditions, we have
Since , this holds for some nonempty subinterval of .
I want to check that I'm following this. Would it be fair to paraphrase the two parts of this inequality as:
1) If your credence that the other player is going to play Stag is high enough, you won't even be tempted to play Hare.
2) If your credence that the other player is going to play Hare is high enough, then it's not defection to play Hare yourself.
?
I guess the rightmost term could be zero or negative, right? (If the difference between T and P is greater than or equal to the difference between P and S.) In that case, the payoffs would be such that there's no credence you could have that the other player will play Hare that would justify playing Hare yourself (or justify it as non-defection, that is).
So my claim #1 is always true, but claim #2 depends on the payoff values.
In other words, Stag Hunt could be subdivided into two games: one where the payoffs never justify playing Hare (as non-defection), and one where they sometimes do, depending on your credence that the other player will play Stag.
It's worth being careful to acknowledge that this set of assumptions is far more limited than the game-theoretical underpinnings. Because it requires interpersonal utility summation, you can't normalize in the same ways, and you need to do a LOT more work to show that any given situation fits this model. Most situations and policies don't even fit the more general individual-utility model, and I suspect even fewer will fit this extension.
That said, I like having it formalized, and I look forward to the extension to multi-coalition situations. A spy can benefit Russia and the world more than they hurt the average US resident.
I very much agree that interpersonal utility comparability is a strong assumption. I'll add a note.