AI ALIGNMENT FORUM
AF

Uncertainty in all its flavours — AI Alignment Forum

Acknowledgements:
This research began during the SERI MATS program, under the joint mentorship of John Wentworth, Nicholas Kees, and Janus. Thanks also to Davidad, Jack Sagar, and David Jaz Myers for discussion.

Abstract:
I think that there is a uniform correspondence between flavours of uncertainty and monads taking state-spaces to belief-state-spaces, for different characterisation of belief. In this essay, I describe this correspondence explicitly and list 15 diverse and well-motivated examples. I explore some applications to model-building and agent foundations. Along the way, I characterise infrabayesianism uncertainty as the minimal way to encompass possibilistic uncertainty, probabilistic uncertainty, and reward.

No prerequisites are required beyond a high-school familiarity with sets, functions, real numbers, etc. Feedback welcome.

Introduction

Suppose I'm facing the following problem. There's an upcoming election between candidates, and you're uncertain who will win. How can I model both your belief about the election and the election itself in a coherent way? By "belief" here, I mean your epistemic attitude, your internal model, your opinion, judgement, prediction, etc, etc. Think map-territory distinction: the election is the territory, your belief is the map, and I need to model both the map and the territory coherently despite the fact that the map and the territory are (typically speaking) two completely different types of thing.

Well, to model the election itself, I'll use a set $S = {s_{1}, s_{2}, s_{3}, \dots s_{n}}$ with an element for each electoral candidate. To represent your belief about the election, I must find another set $B (S)$ with an element for each belief that you might have about the election. I'll call $S$ the state space and $B (S)$ the belief-state space. A solution to our problem is given by a mathematical operator $B$ sending each state-space $S$ to the matching belief-state space $B (S)$ .

One may feel prompted to ask: does any operator $B$ suffice here? Can the belief-state space be anything whatsoever, or must it carry some extra structure, possibly satisfying some additional constraints? Or, stated more philosophically, can any territory serve as a map for any other? I say no. Roughly speaking, the operator $B$ must be a so-called monad, which will be the central object of this essay. But more on that later.

The first thing to note is that the appropriate operator $B$ will depend on how exactly I wish to characterise a "belief" about the election, and there are multiple options here. For example, I might choose to characterise your belief by the set of candidates that you think have a possibility of winning. In this case, $B (S) := P^{+} (S)$ , denoting the set of non-empty subsets of $S$ . Alternatively, I might choose to characterise your belief by the likelihood that you give each candidate. In this case, $B (S) := Δ (S)$ , denoting the set of finite-support probability distributions over $S$ , i.e. functions $p : S \to [0, 1]$ such that ${s \in S : p (s) \neq 0}$ is finite and $\sum s \in S p (s) = 1$ .

In the first option, I'm characterising your belief-state by your possibilistic uncertainty, often encountered in doxastic or epistemic logic. In the second option, I'm characterising your belief-state by your probabilistic uncertainty, which is a finer-grained characterisation of belief because it differentiates between e.g. thinking a coin is fair and thinking a coin is slightly biased.

The second option has its merits. Indeed, many readers will instinctively reach for $Δ$ as soon as they hear the word "uncertainty", and this instinct would serve them well. There's been a fruitful enterprise (in philosophy, mathematics, computer science, linguistics, etc) of replacing possibilistic uncertainty with probabilistic uncertainty in any model or concept where one finds it. But I want to note that both $P^{+}$ and $Δ$ would count as a solution to the problem. I'll return to these two examples throughout this essay because they are the flavours of uncertainty which will be most familiar to the reader.

Flavour of uncertainty	Monad
Possibilistic	Nonempty-powerset monad $P^{+}$
Probabilistic	Distribution monad $Δ$

As we will see, these two operators, $P^{+}$ and $Δ$ , are both monads. The central claim of this essay is that there is a uniform correspondence between flavours of uncertainty and monads. By "flavour of uncertainty" I mean a particular way of characterising someone's potentially uncertain belief about something. Possibilistic and probabilistic are paradigm cases, but in this essay we'll meet fifteen examples.

The forward-implication of this claim, that every flavour of uncertainty is a monad, is perhaps uncontroversial in some circles.^[1] The backwards-implication, that every monad is a flavour of uncertainty, is worthy of more scepticism.

In this essay —

I will describe the correspondence explicitly.
I'll present a step-by-step method for formalising different flavours of uncertainty using monads.
I'll list fifteen examples of the correspondence, which I hope the reader finds well-motivated.
Finally, I'll discuss the relevance to agent foundations, with reference to infrabayesianism in particular.

Don't worry if you don't yet know what monads are. By the end of this essay you'll understand them as well as I do, which is enough to nod along when you hear "monad this" and "monad that".

The correspondence explicitly.

What's a flavour of uncertainty?

Recall from the introduction that I'm tasked with representing or modelling both the election itself and your belief about the election. The first step of this task is to settle on a particular flavour of uncertainty to characterise the belief-states — possibilistic, probabilistic, infrabayesian, etc. One might ask, of this flavour of uncertainty, the following four questions —

Count?
What's counts as a distinct belief about the election? Concretely, if there are $n$ electoral candidates then how many distinct belief-states are there?
Certainty?
If you're certain that a particular candidate will win the election (and I know which candidate) then how should I determine your belief-state?
Collapse?
Suppose a number of forecasters are speculating on the election. If I'm given the belief of each forecaster about the election, and I'm given your belief about the forecasters' beliefs, then how should I determine your belief about the election itself?
Combine?
Suppose there are two completely unrelated elections happening somewhere. If I'm given your belief about the first election, and your belief about the second election, then how should I determine your belief about the pair of elections?

These four questions — Count? Certainty? Collapse? Combine? — are essentially epistemological questions, and they collectively pin down what I mean by a flavour of uncertainty.^[2] As we will see, a monad corresponds to answers to the first three questions and a commutative monad corresponds to answers to all four questions.

Exercise 1: How would you answer these questions for possibilistic uncertainty? Or for probabilistic uncertainty?

Exercise 2: As I mentioned before, an answer to Count? is a set $B (S)$ for each set $S$ . What about for Certainty? Collapse? and Combine?

What's a (commutative) monad?

Monads were born of category theory — a field of mathematics which many regard as arcane, mystical, or downright kabbalistic — but monads can (I think) be understood by someone lacking any acquaintance with category theory whatsoever. Indeed, my claim in this essay is that monads correspond exactly to Map-Territory-like relations, and such relations will be familiar to anyone who's both got a brain and pondered this predicament.

I'll first write down the mathematical definition of a monad, and then I'll explain how this definition mirrors the four epistemological questions.

Definition: A monad $(B, η, ⊳)$ consists of three operators^[3]:
The construct operator $B$ which assigns a set $B (S)$ to each set $S$ .
The return operator $η$ which assigns a function $η_{S} : S \to B (S)$ to each set $S$ .
The bind operator $⊳$ which assigns a function $⊳_{W S} : B (W) \times (W \to B (S)) \to B (S)$ to each pair of sets $W, S$ .
Moreover, a commutative monad $(B, η, ⊳, \otimes)$ is a monad $(B, η, ⊳)$ equipped with a fourth operator:
The product operator $\otimes$ which assigns a function $\otimes_{A B} : B (A) \times B (B) \to B (A \times B)$ to each pair of sets $A, B$ .
These operators must also satisfy some basic algebraic laws to qualify as a (commutative) monad. See here for details.
Notation: I'll use variables $x, x^{'}, x^{''}$ for elements of $X$ , and boldface variables $x, x^{'}, x^{''}$ for elements of $B (X)$ . I may talk loosely of the monad $B$ rather than $(B, η, ⊳)$ or of the commutative monad $B$ rather than $(B, η, ⊳, \otimes)$ . I may write $η^{B}$ , $⊳^{B}$ , or $\otimes^{B}$ for clarification. I may write $w ⊳ f$ instead of $w ⊳_{W S} f$ , and $a \otimes b$ instead of $a \otimes_{A B} b$ .

How do they correspond to each other?

In short, there is an exact correspondence between the operators of a (commutative) monad and the four epistemological questions. Let's go one-by-one.

1. Count?
What's counts as a distinct belief about the election? Concretely, if there are $n$ electoral candidates then how many distinct belief-states are there?

An answer to this question is the constructor operator, assigning a set $B (S)$ to each set $S$ . If $S$ is the set of potential outcomes of an event then $B (S)$ is the set of beliefs about the event.

As we discussed before, for possibilistic uncertainty $B (S) := P^{+} (S)$ , and for probabilistic uncertainty $B (S) := Δ (S)$ .

2. Certainty?
If you're certain that a particular candidate will win the election (and I know which candidate) then how should I determine your belief?

Here, an answer will be the return operator assigning a function $η_{S} : S \to B (S)$ to each set $S$ . If you're certain that a state $s \in S$ will occur, then $η_{S} (s) \in B (S)$ is your belief-state.

For possibilistic uncertainty, $η_{S} (s) := {s} \in P^{+} (S)$ , the singleton set containing $s$ . And for probabilistic uncertainty, $η_{S} (s) := δ_{s} \in Δ (S)$ , the dirac distribution at $s$ given by $δ_{s} : s^{'} \mapsto {\begin{matrix} 1 & if s^{'} = s 0 & otherwise \end{matrix}$ .

The function $η_{S} : S \to B (S)$ describes how the state-space embeds in the belief-state-space. This is related, I think, to the idea that each territory can serve as its own map. (See Borges' On Exactitude in Science for an exploration of this theme.) Or in the words of Norbert Wiener, “The best model of a cat is another, or preferably the same, cat.”

3. Collapse?
Suppose a number of forecasters are speculating on the election. If I'm given the belief of each forecaster about the election, and I'm given your belief about the forecasters' beliefs, then how should I determine your belief about the election itself?

Here, an answer will be the bind operator assigning a function $⊳_{W S} : B (W) \times (W \to B (S)) \to B (S)$ to each pair of sets $W$ and $S$ . You should think of the bind operator as collapsing your second-order beliefs to your first-order beliefs — i.e. if each forecaster $w \in W$ has an first-order belief $f (w) \in B (S)$ , and $w \in B (S)$ is your second-order belief about which forecaster is correct, then $(w ⊳_{W S} f) \in B (S)$ should be your first-order belief about the election.

For possibilistic uncertainty, $w ⊳ f \in P^{+} (S)$ is the union $⋃ w \in w f (w)$ . And for probabilistic uncertainty, $w ⊳ f \in Δ (S)$ is the summation/integral $s^{'} \mapsto \sum w \in w w (s) \cdot f (w) (s^{'})$ .

This is related to the idea that a map of a map of a territory is a map of that same territory; a depiction of a depiction of person is a depiction of that same person, a representation of a representation of an idea is a representation of that same idea; etc.

One might think of $f : W \to B (S)$ as some parameterisation of the belief-state $B (S)$ using some parameters $W$ . Then the bind operator gives us the function for finding your $S$ -belief from you $W$ -belief. Explicitly, this function is $(- ⊳_{W S} f) : B (W) \to B (S), w \mapsto w ⊳_{W S} f$ .

Moreover, the bind operator doesn't just flatten one level of "meta". Often we have an entire hierarchy of state-spaces $S_{0}, S_{1}, S_{2}, \dots, S_{n}$ where beliefs about $S_{i}$ are parameterised by some "higher" state-space $S_{i + 1}$ via a function $f_{i} : S_{i + 1} \to B (S_{i})$ . Here, the state-space $S_{0}$ is the object-level system, the state-space $S_{1}$ parametrises your first-order beliefs about $S_{0}$ , the state-space $S_{2}$ parameterises your second-order beliefs about $S_{1}$ , and so on. Then the bind operator says that I can collapse your $n$ th-order beliefs all the way to your first-order beliefs via the function $(- ⊳ f_{n - 1} ⊳ \dots ⊳ f_{0}) : B (S_{n}) \to B (S_{0})$ .^[4]

4. Combine?
Suppose there are two completely unrelated elections happening somewhere. If I'm given your belief about the first election, and your belief about the second election, then how should I determine your belief about the pair of elections?

An answer will be the product operator $\otimes$ assigning a function $\otimes_{A B} : B (A) \times B (B) \to B (A \times B)$ to each pair of sets $A$ and $B$ . If $a \in B (A)$ is your belief about the first election and $b \in B (B)$ is your belief about an unrelated second election, then $a \otimes_{A B} b \in B (A \times B)$ is your belief about the pair of elections.

For possibilistic uncertainty, $a \otimes b \in P^{+} (A \times B)$ is the cartesian product ${(a, b) \in A \times B : a \in a, b \in b}$ . And for probabilistic uncertainty, $a \otimes b \in Δ (A \times B)$ is the joint distribution $(a, b) \mapsto a (a) \cdot b (b)$ .

Thinking of $S_{1} \times \dots \times S_{n}$ as a factorisation of the state-space $S$ , the product operator implies that your beliefs about each $S_{i}$ combine to yield your overall belief about $S$ . That is, a commutative monad $B$ corresponds to a flavour of uncertainty that you can have to parts of the world, whereas a non-commutative monad $B$ corresponds to a flavour of uncertainty that you can only have to the world in its entirety.

Historical note: The central thesis of this essay is that there is a uniform correspondence between flavours of uncertainty and monads. I call this Myers' correspondence after David Jaz Myers, because I first encountered the idea in his book Categorical Systems Theory, where he devotes a chapter to using commutative monads to model various nondeterminism of automata. Nonetheless, he idea did not originate with him, he's never claimed it is true, and I don't know if he agrees with it.

Examples of Myers' correspondence

The correspondence between he operators of the (commutative) monad and the epistemological questions also serves as a practical recipe for formalising different flavours of uncertainty using monads. I've personally found it useful. First, think about the particular flavour of uncertainty, then answer the Four C's (Count? Certainty? Collapse? Combine?), convert those answers into mathematical operators, and voilà you've got yourself a monad.

I'll now zoom through fifteen examples, beginning (without commentary) with the paradigm examples of $P^{+}$ and $Δ$ .

1 - nonempty powerset monad

Flavour of uncertainty	Possibilistic
Monad	Nonempty powerset
Construct $B (S)$	$P^{+} (S)$
Return $η_{S} (s)$	${s}$
Bind $w ⊳_{W S} f$	$⋃ w \in w f (w)$
Product $a \otimes_{A B} b$	$a \times b$
Interpretation	$x \in x$ if you consider the outcome $x \in X$ to be possible.

2 - distribution monad

Flavour of uncertainty	Probabilistic
Monad	Distribution
Construct $B (S)$	$Δ (S)$
Return $η_{S} (s)$	$δ_{s} : s^{'} \mapsto {\begin{matrix} 1 & if s^{'} = s 0 & otherwise \end{matrix}$
Bind $w ⊳_{W S} f$	$s : s^{'} \mapsto \sum w \in w w (s) \cdot f (w) (s^{'})$
Product $a \otimes_{A B} b$	$(a, b) \mapsto a (a) \cdot b (b)$
Interpretation	$x (x) \in [0, 1]$ is your subjective credence in the outcome $x \in X$ .

3 — reader monad from $H$

Okay, now let's deal with a flavour of uncertainty which is sometimes called "indeterminacy". An indeterminate belief is something like "Well, if $h_{1}$ is true then $x_{1}$ , but if $h_{2}$ is true then $x_{2}$ , but–", i.e. it's a belief which is uncertain because your best guess depends on some unknown variable. More formally, your belief-state is given by a particular function from $H$ (the possible values of the unknown variable) to $S$ (the state-space).

This is an ordinary usage of the word "uncertain" so, by Myers' correspondence, it must correspond to a monad, and we can discover which monad by answering the four Cs. If $S$ is the state-space then the belief-state-space is given by $S^{H}$ , the set of functions $s : H \to S$ . So our construct operator is $(-)^{H}$ . If you're certain tha tthe outcome is $s \in S$ then your belief-state is the constant function $c_{s} : h \mapsto s$ . The intuitive answers to Collapse? and Combine? give us our bind and product operators.

Overall, we get what's called the reader monad from $H$ .

Flavour of uncertainty	$H$ -indeterminacy
Monad	Reader monad from $H$
Construct $B (S)$	$S^{H}$
Return $η_{S} (s)$	$c_{s} : h \mapsto s$
Bind $w ⊳_{W S} f$	$h \mapsto f (w (h)) (h)$
Product $a \otimes_{A B} b$	$h \mapsto (a (h), b (h))$
Interpretation	$x (h) = x$ if $x \in X$ is your best guess about the outcome conditioned on the information $h \in H$ .

4 — writer monad to $[0, 1]$

Often, people will report their uncertain beliefs like "The coin will land heads (98%)" or "AI will disempower humanity (60%)". That is, their belief is a best guess paired with their confidence, which they offer as a lower-bound on the likelihood of that their guess is correct. A certain belief-state would be something like "The coin will land heads (100%)".

What monad corresponds to this flavour of uncertainty?

If $S$ is the state-space then $S \times [0, 1]$ is the belief-state-space, i.e. there's a distinct belief-state for each pair $s = (s, q) \in S \times [0, 1]$ . If you're certain that the outcome is $s \in S$ then your belief-state is $(s, 100 %) \in S \times [0, 1]$ . Uncertainty is collapsed by multiplying the confidences. Uncertainty is combined also by multiplying the confidences.

Ta-da! The writer to $[0, 1]$ monad..

Flavour of uncertainty	Confidence-marked guess
Monad	Writer to $[0, 1]$ monad
Construct $B (S)$	$S \times [0, 1]$
Return $η_{S} (s)$	$(s, 1.00)$
Bind $w ⊳_{W S} f$	$(s, p \cdot q)$ where $w = (w, p)$ and $f (w) = (s, q)$
Product $a \otimes_{A B} b$	$((a, b), p \cdot q)$ where $a = (a, p)$ and $b = (b, q)$ .
Interpretation	$x = (x, p)$ if $p \in [0, 1]$ is your confidence in the outcome $x \in X$ , i.e. you think that the likelihood of $x \in X$ is at least $p$ .

Using the writer to $[0, 1]$ monad, we've characterised a belief-state as an outcome marked with some additional metadata, namely a confidence $p \in [0, 1]$ . What properties of the interval $[0, 1]$ did we appeal to in this definition? Well, firstly that we can multiply different elements (see bind and product operators). And secondly, that there's a fixed element such that multiplying with this element does nothing (see return operator).

Hence we can generalise: given any monoid $(M, e, ⊙)$ we have a monad $B (S) = S \times M$ called the writer-to- $M$ monad.^[5] By using different monoids, we can model different flavours of uncertainty, but note that this is only a commutative monad when $(M, e, ⊙)$ is a commutative monoid.

There's another ordinary usage of the word "uncertainty" where an uncertain belief would be something like "AGI arrives before 2040 unless there's a nuclear war" and a certain belief would be something like "AI will arrive before 2040." At least, with regards to teh binary question of whether AGI arrives before 2040. That is, an uncertain belief is one with an "unless..." clause.

Formalising this, we have a fixed set of events $F$ , and a belief-state is a pair $(s, E) \in S \times F$ . Your belief-state is $(s, E)$ when you commit to the state $s \in S$ occurring unless the event $E \in F$ occurs. This flavour of uncertainty corresponds to the writer monad $B (S) = S \times F$ , where $F$ is a monoid when equipped with union $\cup : F \times F \to F$ and the empty set $\emptyset \in F$ .

One might use this flavour of uncertainty to models various kinds of defeasible reasoning, where a belief-state $(s, E)$ is characterised by the precondition $E$ under which the belief would be defeated or disavowed.

Flavour of uncertainty	Unless-claused guess
Monad	Writer monad to $F$
Construct $B (S)$	$S \times F$
Return $η_{S} (s)$	$(s, \emptyset)$
Bind $w ⊳_{W S} f$	$(s, E_{1} \cup E_{2})$ where $w = (w, E_{1})$ and $f (w) = (s, E_{2})$
Product $a \otimes_{A B} b$	$((a, b), E_{1} \cup E_{2})$ where $a = (a, E_{1})$ and $b = (b, E_{2})$ .
Interpretation	$x = (x, E)$ if you think $x$ will occur unless event $E$ occurs.

Or maybe an uncertain belief is a one full of amendments, clarifications, conditions, disclaimers, excuses, hedges, limitations, qualification, refinements, reservations, restrictions, stipulations, temperings, etc. By contrast, a certain belief is made "with no ifs or buts", bare and direct.

Formalising this, we have a fixed set of clarifications $C$ , and a belief-state is a pair $(s, l) \in S \times List (C)$ . Here, $List (C)$ is the free monoid over the set of clarifications $C$ equipped with concatenation $+ : List (C) \times List (C) \to List (C)$ and the empty list $[] \in List (C)$ .

Flavour of uncertainty	Clarified guess
Monad	Writer to $List (C)$ monad
Construct $B (S)$	$S \times List (C)$
Return $η_{S} (s)$	$(s, [])$
Bind $w ⊳_{W S} f$	$(s, l_{1} + l_{2})$ where $w = (w, l_{1})$ and $f (w) = (s, l_{1} + l_{2})$
Product $a \otimes_{A B} b$	N/A (See below.)
Interpretation	$x = (x, l)$ if you think $x$ will occur and $l$ is a list of your clarifications.

Now, the writer to $List (C)$ monad isn't a commutative monad. Or interpreted philosophically, a clarified guess isn't the kind of uncertainty you can have to parts of the world. Suppose "I think Alice is happy but I don't know her very well" is my belief-state about Alice, and "I think Bob is happy but he's difficult to read" is my belief-state about Bob. What's my belief-state about both Alice and Bob? Is it (1) "Alice and Bob are both happy, but I don't know Alice very well and Bob is difficult to read" or (2) "Alice and Bob are both happy, but Bob is difficult to read and I don't know Alice very well". That is, in which order should we combine the clarifications?

The instinctive trick is to declare that two belief-states are equal if the lists of clarifications are equal up-to-permutation — this implies that (1) and (2) are the same belief-state, which does seem intuitive to me. If we play this trick, then the resulting flavour of uncertainty is captured by the writer-to- $N [C]$ monad, where $N [C]$ is the free commutative monoid. This does indeed give a commutative monad!

Flavour of uncertainty	Unordered clarified guess
Monad	Writer monad to $N [C]$
Construct $B (S)$	$S \times N [C]$
Return $η_{S} (s)$	$(s, 0)$
Bind $w ⊳_{W S} f$	$(s, l_{1} + l_{2})$ where $w = (w, l_{1})$ and $f (w) = (s, l_{1} + l_{2})$
Product $a \otimes_{A B} b$	$((a, b), l_{1} + l_{2})$ where $a = (a, l_{1})$ and $b = (b, l_{2})$ .
Interpretation	$x = (x, l)$ if you think $x$ will occur and $l$ is an unordered list of your clarifications.

5 — identity monad

If we've anticipating an election between $n$ candidates, then the simplest way to characterise your belief about the election by your best guess with no additional information about how unsure you are. If $S$ is the state-space then $S$ is also the belief-state-space, i.e. there's a distinct belief-state for each $s \in S$ . The set of belief-states is therefore equal (up to bijection) to the set of outcomes itself.

I'll admit that this flavour of uncertainty is somewhat degenerate — e.g. every belief-state is a certainty in some particular state — but it's worth including nonetheless. On some readings of Wittgenstein's Tractatus, this is his model of how language represents the world, our utterances stand in direct isomorphism with the state-of-affairs.

Anyway, answering the four Cs would give the identity monad!

Flavour of uncertainty	Best guess
Monad	identity monad
Construct $B (S)$	$S$
Return $η_{S} (s)$	$s$
Bind $w ⊳_{W S} f$	$f (w)$
Product $a \otimes_{A B} b$	$(a, b)$
Interpretation	$x = x$ if $x \in X$ is your best guess about the outcome

6 — maybe monad

The last example was a bit silly, so how about this instead..?

If we've anticipating an election between $n$ candidates, then I'll characterise your belief about the election either by your best guess (with no additional information) or an "I don't know" response. This is an very coarse-grained flavour of uncertainty — the only belief-state about the election (other than certainty in a particular candidate) is the belief-state of utter cluelessness, or shrugging one's shoulders!

Despite the coarse-grained-ness, it's pretty commonly encountered in the wild. For example, it's the typical flavour of uncertainty encountered in surveys/questionnaires, where $⊥$ is read as "no opinion/don't know". It's also encountered in voting, where $⊥$ is read as "abstention".

Formally speaking, if $S$ is the state-space then there's a distinct belief-state for each state $s \in S$ plus an additional option denoted $⊥$ . The belief-state-space is therefore $S + 1$ , denoting the disjoint union of $S$ with the singleton set ${⊥}$ . If you're certain that the outcome is $s \in S$ then your belief-state is $s \in S$ . This flavour of uncertainty corresponds to the famous maybe monad.

Flavour of uncertainty	guess-or-shrug
Monad	maybe monad
Construct $B (S)$	$S + 1$
Return $η_{S} (s)$	$s$
Bind $w ⊳_{W S} f$	${\begin{matrix} ⊥ & if w = ⊥ f (w) & otherwise \end{matrix}$
Product $a \otimes_{A B} b$	${\begin{matrix} ⊥ & if a = ⊥ or b = ⊥ (a, b) & otherwise \end{matrix}$
Interpretation	$x = x$ if $x \in X$ is your best guess for the outcome, and $x = ⊥$ if you offer no best guess.

7 — $K$ -distribution monad

You might, at this point, feel short-changed. I've discussed so far a range of flavours of uncertainty which are all coarser-grained than probabilistic knowledge, so why not stick to $Δ$ ? Let's consider then a more fined-grained characterisation of belief-state, one that tracks infinitesimal differences between probability assignments.

The Levi-Civita Field is an extension of the real numbers which contains infinitesimal values like $ϵ, ϵ^{2}, 2 ϵ + ϵ^{2}, π^{2} \sqrt{ϵ}$ and infinite values like $ϵ^{- 1}, ϵ^{- 2}, ϵ^{1 / 3} + ϵ^{- 1 / 3} + 2$ . We can replace $[0, 1]$ in the definition of $Δ$ with $LCF$ to obtain a monad $Δ_{LCF}$ corresponding this flavour of uncertainty. On this account, a belief-state $x \in Δ_{LCF} (X)$ is something which tracks the potentially infinitesimal likelihood $x (x) \in LCF$ of each outcome $x \in X$ . This flavour of uncertainty has applications in infinite ethics and cooperation in large worlds.

For example, in a universe with infinite radius $ϵ^{- 1}$ , what's your prior likelihood that you occupy the most central galaxy? Presumably, the likelihood should be $ϵ^{3} / ρ \in LCF$ , where $ρ \in R^{+}$ is the density of galaxies.

Now suppose you were offered a lottery which promises to benefit everyone by $δ$ if you indeed occupy the most central galaxy but otherwise benefits no one. What's this lottery worth? Presumably, it's worth $δ$ , because the infinitary stakes $δ \cdot ρ \cdot ϵ^{- 3}$ are cancelled out by the infinitesimal chance of winning $ϵ^{3} / ρ$ .

Note that because $LCF$ is totally-ordered, once we assign $LCF$ values to different lotties, we can perform expected utility maximisation as usual, and get sensible results. I think that infinitesimal probabilities resolves some (but not all) problems in infinite ethics. I'm particularly lured by the hope that, in an infinite cosmos, the infinitary stakes might somehow cancel out with infinitesimal probabilities to yield finite values. See Joe Carlsmith's essay On Infinite Ethics for further discussion.

Flavour of uncertainty	infinitesimal probabilistic
Monad	$LCF$ -distribution monad
Construct $B (S)$	$Δ_{LCF} (S)$
Return $η_{S} (s)$	$δ_{s} : s^{'} \mapsto {\begin{matrix} 1 & if s^{'} = s 0 & otherwise \end{matrix}$
Bind $w ⊳_{W S} f$	$s : s^{'} \mapsto \sum w \in w w (s) \cdot f (w) (s^{'})$
Product $a \otimes_{A B} b$	$(a, b) \mapsto a (a) \cdot b (b)$
Interpretation	$x (x) \in LCF$ is your potentially infinitesimal subjective credence in the outcome $x \in X$

How far can one generalise the kind of entity that a "probability" must be, before our definition breaks? Well, so long as we have some rig $K$ , we can define a monad $Δ_{K}$ by replacing $[0, 1]$ with $K$ . A rig is a set $K$ equipped with a zero element $0 \in K$ , a unit element $1 \in K$ , an addition function $\oplus : K \times K \to K$ , and a multiplication function $\otimes : K \times K \to K$ , satisfying certain algebraic laws. By choosing different rigs $K$ then we obtain different monads $Δ_{K}$ corresponding to different flavours of uncertainty.

When $K := [0, 1]$ we obtain the ordinary probability distributions, and when $K := Q \cap [0, 1]$ we obtain the rational probability distributions, etc. Toby Fritz suggests that by using similar tricks we might obtain quantum uncertainty, fuzzy uncertainty, and Dempster–Shafer uncertainty, but I haven't checked whether this is true.

Flavour of uncertainty	$K$ -probabilistic
Monad	$K$ -distribution monad
Construct $B (S)$	$Δ_{K} (S)$
Return $η_{S} (s)$	$δ_{s} : s^{'} \mapsto {\begin{matrix} 1 & if s^{'} = s 0 & otherwise \end{matrix}$
Bind $w ⊳_{W S} f$	$s : s^{'} \mapsto \sum w \in w w (s) \cdot f (w) (s^{'})$
Product $a \otimes_{A B} b$	$(a, b) \mapsto a (a) \cdot b (b)$
Interpretation	$x (x) \in K$ is your subjective credence in the outcome $x \in X$ , where $K$ is whatever rig of exotic probabilities

8 — quantum monad

For sure, quantum mechanics is endowed with its own flavour of uncertainty, hence the term Heisenberg's Uncertainty Principle. It's not impossible to catch a physicist saying "it's uncertain whether the qubit is 0 or 1" or "it's uncertain whether the cat is alive or dead", regardless of whether they consider quantum uncertainty as strictly speaking epistemic. By Myers' correspondence, this flavour of uncertainty must correspond to a monad.

Exercise 3: Which?^[6]

9 — smooth state monad

The position of the North Star in the night sky is constant, static, immutable, certain; the position of Mercury, by contrast, is variable, dynamic, mutable, uncertain. Is this not a common sense of the word? Might one not say that my belief-state about Mercury's position will forever be uncertain, no matter how accurate my telescope or exhaustive my calculations, because my belief is always revised? If so, then by Myers' correspondence this flavour of uncertainty corresponds to a monad.

To formalise this, let's fix a differentiable manifold $Θ$ parameterising your internal mental state as you think about a question. Note that because $Θ$ is a differentiable manifold, it's equipped with tangent space $T_{θ}$ at every $θ \in Θ$ .

If $S$ is the state-space, then $\prod_{θ \in Θ} (S \times T_{θ})$ is your belief-state-space. In other words, we have a distinct belief-state for each smooth transition function $s \in \prod_{θ \in Θ} (S \times T_{θ})$ . A belief-state $s$ is characterised by a pair $s (θ) = (s, v)$ for each $θ \in Θ$ , where $s \in S$ is your current guess and $v \in T_{θ}$ is the tangent vector describing how your mental state is evolving. If you're certain that the winner is $s \in S$ then your belief-state is the static transition function $η (s) : θ \mapsto (s, 0)$ where $0 \in T_{θ}$ is the zero vector.

This is the smooth state monad — it's a differentiable version of the discrete-time state monad, with the additional benefit that it's commutative monad.

Flavour of uncertainty	evolving guess
Monad	smooth state monad
Construct $B (S)$	$\prod_{θ \in Θ} (S \times T_{θ})$
Return $η_{S} (s)$	$θ \mapsto (s, 0)$
Bind $w ⊳_{W S} f$	$θ \mapsto (s, v_{1} + v_{2})$ where $w (θ) = (w, v_{1})$ and $f (w) (θ) = (s, v_{2})$
Product $a \otimes_{A B} b$	$θ \mapsto ((a, b), v_{1} + v_{2})$ where $a (θ) = (a, v_{1})$ and $b (θ) = (b, v_{2})$ .
Interpretation	The transition function $x : \prod_{θ \in Θ} (X \times T_{θ})$ describes how your internal mental state evolves over time and produces guesses.

10 — continuation monad

What are belief-states actually for anyway? What purpose do they play in rational decision-making? According to one school of thought, belief-states are simply gadgets for taking expected values, and chiefly for taking expected utility values.

Let's say $S$ is the set of candidates running in the election, and $v : S \to R$ is your utility function, i.e. $v (s) \in R$ measures how happy you'd be to hear that the candidate $s \in S$ has won. Then your ex-ante utility is some $r \in R$ measuring how happy you are now in anticipation of the outcome. Given your belief-state, I should be able to determine $r \in R$ from $v : S \to R$ , which implies that I can just characterise your belief-state about the election by how $r \in R$ is determined from $v : S \to R$ . Neat.

This is formalised by the so-called continuation to $R$ monad. If $S$ is the state-space then $K (S, R)$ is the belief-state-space, where $K (S, R)$ is the set of functionals $s : (S \to R) \to R$ . And a belief-state $s : (S \to R) \to R$ is certain in the outcome $s \in S$ if $s$ determines your ex-ante utility simply by evaluating your utility function at $s$ , i.e. $s = λ^{v : S \to R} . v (s)$ .

The continuation monad encompasses both possibilistic uncertainty and probabilistic uncertainty. If the nonempty subset $A \in P^{+} (X)$ models your possibilistic uncertainty then the associated functional $x \in K (X, R)$ is given by $λ^{v : X \to R} . min {v (x) : x \in A}$ . If the distribution $μ \in Δ (X)$ models your probabilistic uncertainty then the associated functional $x \in K (X, R)$ is given by $λ^{v : X \to R} . E_{x \sim μ} [v (x)]$ .

Flavour of uncertainty	ex-ante utility
Monad	Continuation monad
Construct $B (S)$	$K (S, R)$
Return $η_{S} (s)$	$v \mapsto v (s)$
Bind $w ⊳_{W S} f$	$w (λ^{w \in W} . f (w) (v))$
Product $a \otimes_{A B} b$	Unfortunately, $K (-, R)$ is not a commutative monad.^[7]
Interpretation	If $v : X \to R$ assigns your ex-post utility $v (x) \in R$ to each outcome $x \in X$ , then $x (v) \in R$ is your ex-ante utility.

Exercise 4: (Beginner) Prove that the two maps $P^{+} (X) \to K (X, R)$ and $Δ (X) \to K (X, R)$ are injections. (Advanced) Prove these injections are monad transformers.^[8]

11 — signature monad

Maybe I should characterise your belief-state about something by the sentence that you'd utter about the outcome. This will result in a more syntactic or linguistic account of belief. You might imagine here a shared language, like English or Python, with which a speaker may report their beliefs to a friend. Or you might imagine a private mental language in which a brain/AI will store their knowledge about the world.

To make this rigorous, I must introduce a language containing all the sentences that you might utter about the outcome. Our language will include an atomic sentence $┌ s ┐$ for every outcome $s \in S$ , along with certain connectives for combining sentences. For example, suppose we have a language with two symbols, a binary connective $\lor$ called disjunction and a unary connective $\neg$ called negation. If $S := {s_{1}, \dots, s_{n}}$ are the candidates in an election, then a belief-state about the electoral outcome is a sentence like $┌ s_{5} ┐$ or $┌ (s_{2} \lor \neg s_{3}) \lor \neg (s_{4} \lor s_{6}) ┐$ .

The logical connectives can be specified by a signature $(Σ, arity : Σ \to N}$ . A signature is a set $Σ$ equipped with a map $arity : Σ \to N$ sending each connective to its arity. So the aforementioned language has the signature $Σ = {\lor, \neg}$ with $arity (\lor) = 2$ and $arity (\neg) = 1$ .

We denote the resulting set of sentences by $L (Σ, S)$ . This is a set containing all the sentences freely generated from $S$ using the connectives in $Σ$ . Explicitly, $L (Σ, S)$ is the smallest set such that $┌ s ┐ \in L (Σ, S)$ for every $s \in S$ and $┌ σ (ϕ_{1}, \dots, ϕ_{k}) ┐ \in L (Σ, S)$ for every $σ \in Σ$ , $arity (σ) = k$ , and $┌ ϕ_{i} ┐ \in L (Σ, S)$ .

With this machinery in place, we can answer the Four C's, and thereby find the corresponding monad.

If $S$ is the state-space then there's a distinct belief-state for each sentence $s \in L (Σ, S)$ .
If you're certain that the winner of the election is $s \in S$ , then your belief-state is the sentence $┌ s ┐$ .
Let $f : W \to L (Σ, S)$ be the function assigning to each forecaster $w \in W$ their belief-state $f (w) \in L (Σ, S)$ about the election. And let $w \in L (Σ, W)$ be your belief-state about the forecasters. Then your belief $s \in L (Σ, S)$ about the election itself is given by uniform substitution: loop through the sentence $w \in L (Σ, W)$ and, every time you come across an atomic letter $w \in W$ , replace it with the sentence $f (w) \in L (Σ, W)$ . This results in a sentence $s \in L (Σ, S)$ .^[9]
Unfortunately, $L (Σ, -)$ isn't generally a commutative monad.^[10]

Flavour of uncertainty	utterance in a language
Monad	signature monad $L (Σ, -)$
Construct $B (S)$	$L (Σ, S)$
Return $η_{S} (s)$	$┌ s ┐$
Bind $w ⊳_{W S} f$	Uniform substitution of every $w \in W$ with $f (w) \in L (Σ, S)$ in the sentence $w$
Product $a \otimes_{A B} b$	N/A
Interpretation	$x \in L (Σ, X)$ is the sentence that you would utter about the outcome, in a language which contains an atomic letter for each outcome $x \in X$ and a logical connective for each $σ \in Σ$ .

Many monads are equivalent to $L (Σ, -)$ for some signature $Σ$ , including many monads we've already encountered.

When $Σ = \emptyset$ , then $L (Σ, -)$ is equivalent to the identity monad. This is intuitive. If there's no connectives in the language, then every utterance is a single atomic sentence positing one of the outcomes.
When $Σ = {⊥}$ consists of one constant symbol (i.e. zero-arity connective) then $L (Σ, X)$ will contain the atomic sentences $┌ x ┐$ plus one additional sentence $┌ ⊥ ┐$ . So $L (Σ, -)$ is equivalent to the maybe monad. We encountered this before as modelling the guess-or-shrug flavour of uncertainty.
When $Σ = {⊥, ⊥^{'}, ⊥^{''}, \dots}$ consists of many constant symbols, then $L (Σ, X)$ will contain atomic sentences $┌ x ┐$ plus additional sentences $┌ ⊥^{(k)} ┐$ for every $⊥^{(k)} \in Σ$ . So $L (Σ, -)$ is equivalent to what's called the exception monad $(- + Σ)$ . This is like the guess-or-shrug, except there are multiple ways to shrug one's shoulders.
When $Σ = {\neg}$ consists of one unary connective, then $L (Σ, X)$ will contain sentences like $┌ \neg \neg \neg \neg x ┐$ . So $L (Σ, -)$ is equivalent to the writer monad to the monoid $(N, +, 0)$ . If $Σ$ consists of many unary connectives, then $L (Σ, -)$ is equivalent to the writer monad to $List (Σ)$ . We encountered this before as modelling the clarified guess.
When $Σ = {\lor}$ consists of one a binary connective, then $L (Σ, X)$ will consist of sentences like $┌ (x_{1} \lor ((x_{2} \lor x_{2}) \lor x_{3})) \lor (x_{5} \lor x_{8})) ┐$ . So $L (Σ, -)$ is equivalent to the set of full binary trees over $X$ . As Vanessa Kosoy notes, "we think of such a tree as a way to select an element of $X$ by reading a stream of bits." (See here.)

Isn't the archetypal symbol of uncertainty... a fork in the road? Imagine a traveller facing two paths, left and right, each forking further ahead, and so on unboundedly, forming a fractal canopy of binary choices.

12 — algebraic theory

There's something a bit perverse about characterising your belief-state with a single utterance about the outcome. Namely, some utterances will be logically equivalent to each other, such as $┌ ϕ ┐$ and $┌ (ϕ \lor ϕ) ┐$ , and therefore the belief-state in which you're willing to utter $┌ ϕ ┐$ is the exact same as the belief-state in which you're willing to utter $┌ (ϕ \lor ϕ) ┐$ , assuming that you're both rational and honest. Therefore, our previous characterisation was overcounting the belief-states by distinguishing logically-equivalent sentences. Bizarrely, there would be infinitely-many belief-states about a single coin flip — i.e. $┌ H ┐$ , $┌ (H \lor H) ┐$ , $┌ (H \lor (H \lor H)) ┐$ , and so on.

To fix this, what we need isn't just a signature $Σ$ , but rather a signature $Σ$ paired with a set $E$ of equational axioms, which is called an algebraic theory. An equational axiom is a pair of sentences built using the connectives in $Σ$ and some placeholder sentence variables ${a, b, c, \dots}$ . We use $E$ to define an equivalence relation $\sim_{E}$ on $L (Σ, X)$ by taking the deductive closure of the axioms, and then the equivalence classes of the sentences will be our belief-states.

For example, if our signature is ${\lor}$ and we intend to interpret the $\lor$ connective as disjunction, then $E$ should consist of three axioms:

Idempotency, $(a \lor a) = a$
Commutativity, $(a \lor b) = (b \lor a)$
Associativity, $((a \lor b) \lor c) = (a \lor (b \lor c))$

Furnished with the concept of an algebraic theory, we can now improve our answers:

If $S$ is the state-space then there is a distinct belief-state for each equivalence class of sentences $[ϕ]^{E} := {┌ ψ ┐ \in L (Σ, Y) : ┌ ϕ ┐ \sim_{E} ┌ ψ ┐}$ . This set is denoted $L (Σ, E, Y) := {[ϕ]^{E} : ϕ \in L (Σ, Y)}$ .
If you're certain that the winner is $s \in S$ , then your belief-state is the sentence $[s]^{E} \in L (Σ, E, S)$ .
Let $f : W \to L (Σ, E, S)$ be the function assigning to each forecaster $w \in W$ their belief-state $f (w) \in L (Σ, E, S)$ about the election. And let $w \in L (Σ, E, W)$ be your belief-state about the forecasters. Then your belief $s \in L (Σ, E, S)$ about the election itself is given by uniform substitution modulo equivalence. We know $w = [ϕ]^{E}$ for some $┌ ϕ ┐ \in L (Σ, W)$ and that $f (w) = [F (w)]^{E}$ for some $F : W \to L (Σ, S)$ . Then $w ⊳ f = [ϕ ⊳_{W S}^{L (Σ, -)} F]^{E}$ where $⊳_{W S}^{L (Σ, -)}$ is the bind operator for the signature monad. This is operation is well-defined because the deductive system satisfies referential transparency — i.e. if $┌ ϕ_{i} ┐ \sim_{E} ┌ ϕ_{i}^{'} ┐$ then $┌ σ (ϕ_{1}, \dots, ϕ_{n}) ┐ \sim_{E} ┌ σ (ϕ_{1}^{'}, \dots, ϕ_{n}^{'}) ┐$ .
Again, $L (Σ, E, -)$ isn't generally a commutative monad.

Flavour of uncertainty	equivalence class of utterances
Monad	utterances-modulo-equivalence
Construct $B (S)$	$L (Σ, E, S)$
Return $η_{S} (s)$	$[s]^{E}$
Bind $w ⊳_{W S} f$	$[ϕ ⊳_{W S}^{L (Σ, -)} F]^{E}$ where $w = [ϕ]^{E}$ and $\forall w \in W . f (w) = [F (w)]^{E}$
Product $a \otimes_{A B} b$	N/A
Interpretation	$x \in L (Σ, E, X)$ is the set of sentence that you would assert about the outcome, in a language which contains an atomic letter for each outcome $x \in X$ , a logical connective for each $σ \in Σ$ , and where $E$ is the set of equational axioms governing the connectives of $Σ$ .

If a monad $B$ is equivalent to $L (Σ, E, -)$ for some algebraic theory $(Σ, E)$ then we call $(Σ, E)$ a presentation of the monad.^[11] A presentation of a monad is a rather nice description of a flavour of uncertainty via some operators for defining belief-states in terms of other belief-states and some rules governing those operators.

When $E$ is empty, then $L (Σ, E, -)$ is obviously just the signature monad $L (Σ, -)$ .
When $Σ = {□_{p} : p \in [0, 1]}$ contains a unary connective for every $p \in [0, 1]$ and $E$ contains the axioms $□_{p} □_{q} a = □_{p \cdot q} a$ , then $L (Σ, E, X)$ is equivalent to the writer monad to the monoid $[0, 1]$ . We encountered this before as the confidence-marked guess. In general, we can give a similar presentation for the writer monad to any monoid $(M, e, ⊙)$ . So the unless-claused guess has a similar presentation.
When $Σ = {\lor}$ and $E$ is idempotency, commutativity, and associativity (shown above), then there is a distinct class $[ϕ]^{E} \in L (Σ, E, X)$ for each non-empty finite subset of $X$ . So $L (Σ, E, -)$ is equivalent to the nonempty finite powerset monad $P_{f}^{+}$ . This is a finitary version of the monad $P^{+}$ which we've encountered as modelling possibilistic uncertainty. This algebraic theory is also called the theory of semilattices.
Let's find a presentation for $Δ$ the distribution monad. The signature ${+_{p} : p \in (0, 1)}$ will contain a binary connective for every $p \in (0, 1)$ . Our axioms will be $a +_{p} a = a$ (skew-idempotency), $a +_{p} b = b +_{1 - p} a$ (skew-commutativity), and $((a +_{p} b) +_{q} c) = (a +_{p \cdot q} (b +_{\frac{(1 - p) \cdot q}{1 - p \cdot q}} c))$ for (skew-associativity). You should think of $┌ ϕ +_{p} ψ ┐$ as $p$ units of $┌ ϕ ┐$ and $(1 - p)$ units of $┌ ψ ┐$ , which explains the ghastly expression for skew-associativity. This algebraic theory is called the theory of convex algebras.

Exercise 5: Find a presentation for $Δ_{K}$ for an arbitrary rig $K$ .

13 — convex powerset of distributions monad

As we saw before, the continuation monad $K (-, R)$ encompasses both possibilistic and probabilistic uncertainty. Unfortunately $K (-, R)$ lacks any presentation, even if we allow connectives with infinite arity!^[12] Fortunately, there exists a monad encompassing both possibilistic and probabilistic uncertainty which is presentable.

Recall that the nonempty finite powerset monad $P_{f}^{+}$ , which corresponds to possibilistic uncertainty, is presented by the theory of semilattices $(Σ_{1}, E_{1})$ . And the distribution monad $Δ$ , which corresponds to probabilistic uncertainty, is presented by the theory of convex algebras $(Σ_{2}, E_{2})$ . Consider the theory $(Σ_{1} \cup Σ_{2}, E_{1} \cup E_{2} \cup D)$ where $D = {a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)}$ is an additional axiom of describing how the $+_{p}$ connectives distribute over the $\lor$ connective.

This new theory is a presentation the convex powerset of distributions monad. This monad, denoted by $C$ , corresponds to a flavour of uncertainty wherein a belief-state is a convex set of distributions, e.g. "The coin lands either heads (20-30%) or tails (70-80%)." (See credal sets.)

Now, we could have defined $C$ in an entirely non-syntactic way, i.e. " $C (X)$ is the set of nonempty finitely-generated convex-closed sets of finite-support distributions over $X$ ." But I think the syntactic definition, in terms of the algebraic theories for $P^{+}$ and $Δ$ , elucidates why $C$ is a well-motivated unification of probabilistic and possibilistic uncertainty. We will employ a similar strategy for motivating infrabayesianism — roughly speaking, infrabayesianism is exactly what you get when you combine probabilistic and possibilistic uncertainty with reward.

Flavour of uncertainty	imprecise probability
Monad $L (Σ, E, -)$	convex powerset of distributions monad
Signature $Σ$	${\lor} \cup {+_{p} : p \in (0, 1)}$
Axioms $E$	$\lor$ is semilattice, i.e. $a \lor a = a$ $a \lor b = b \lor a$ $a \lor (b \lor c) = (a \lor b) \lor c$ ${+_{p} : p \in (0, 1)}$ is convex algebra, i.e. $a +_{p} a = a$ $a +_{p} b = b +_{1 - p} a$ $((a +_{p} b) +_{q} c) = (a +_{p \cdot q} (b +_{\frac{(1 - p) \cdot q}{1 - p \cdot q}} c))$ $+_{p}$ distributes over $\lor$ , i.e. $a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)$
Interpretation	$┌ x ┐$ is certainty in an outcome $x \in X$ . $┌ ϕ_{1} \lor ϕ_{2} ┐$ is possibilistic uncertainty between $┌ ϕ_{1} ┐$ and $┌ ϕ_{2} ┐$ . $┌ ϕ_{1} +_{p} ϕ_{2} ┐$ is probabilistic uncertainty between $┌ ϕ_{1} ┐$ (with chance $p$ ) and $┌ ϕ_{2} ┐$ (with chance $1 - p$ ).

14 — free convex lattice monad

There's a common usage of the word "uncertainty", where the uncertainty is modulo strategic choice. For example, you might hear "Black is certain to win" from a chess commentator if Black can force a checkmate, or hear "the winner is still uncertain" from a poker commentator during the flop. By Myers' correspondence, this flavour of uncertainty — call it "ludic uncertainty" — must correspond to some monad, but which?

Consider the theory of convex lattices — with signature $Σ_{G} = {\lor, \land, 0, 1} \cup {+_{p} : p \in (0, 1)}$ and the following axioms:

$(\lor, \land, 0, 1)$ is a lattice.^[13]
${+_{p} : p \in (0, 1)}$ is a convex algebra.
$+_{p}$ distributes over $\lor$ and $\land$ , i.e. $a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)$ and $a +_{p} (b \land c) = (a +_{p} b) \land (a +_{p} c)$ .

Then $G := L (Σ_{G}, E_{G}, -)$ is a monad corresponding, I think, to the aforementioned flavour of uncertainty. It sends a set $X$ to the set $G (X)$ , the free convex lattices over $X$ . An element of $G (X)$ should be read as a game-tree whose non-leaf nodes are either a free binary choice by White, a free binary choice by Black, or a biased coin flip. The leaf nodes may be either wins for White, wins for Black, or an element of the set $X$ .

We treat game-trees $g, g^{'} \in G (X)$ as equivalent if the same outcome would result from $g$ and $g^{'}$ regardless of the player's preferences over the elements of $X$ . For example, the lattice axioms $ϕ \lor 0 = ϕ$ and $ϕ \land 1 = ϕ$ will hold because no player would willingly choose to loose, and the axioms $ϕ \lor (ϕ \land ψ) = ϕ$ and $ϕ \land (ϕ \lor ψ) = ϕ$ establish that the players are adversarial, i.e. would never willingly empower one another.

Exercise 7: Consider the game $┌ ((1 \lor x_{2}) \land ((x_{2} +_{0.8} 0) \lor (x_{2} \land 1))) \land (x_{2} \lor (x_{5} +_{0.5} (x_{3} \land x_{4}))) ┐$ shown below. Which outcome is (ludically) certain?

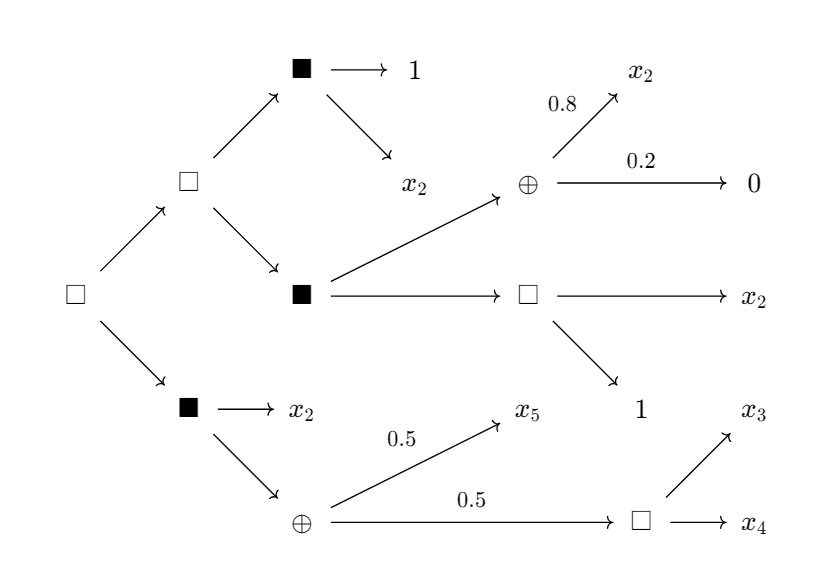
The outcome of the game $┌ ((1 \lor x_{2}) \land ((x_{2} +_{0.8} 0) \lor (x_{2} \land 1))) \land (x_{2} \lor (x_{5} +_{0.5} (x_{3} \land x_{4}))) ┐$ is certain.

Note that $G (X)$ aren't really games in the usual sense, because leaf nodes might be elements of $X$ , and we treat these elements are pairwise incomparable to both players. So you should think of $G (X)$ as a set of partially-specified game trees. A fully-specified game tree would be an element of $G ([0, 1])$ , which is a game tree where each leaf-node returns some $[0, 1]$ -valued utility to Black and disutility to White. You may notice that $[0, 1]$ can itself be equipped with the structure of a convex lattice, which just means there exists a $G$ -algebra $V : G ([0, 1]) \to [0, 1]$ .^[14] This $G$ -algebra is exactly the well-known used in combinatorial game theory.

Flavour of uncertainty	ludic
Monad $L (Σ, E, -)$	free convex lattices
Signature $Σ$	${\land, \lor, 0, 1} \cup {+_{p} : p \in (0, 1)}$
Axioms $E$	${\land, \lor, 0, 1}$ is a lattice. ${+_{p} : p \in (0, 1)}$ is convex algebra. $+_{p}$ distributes over both $\land$ and $\lor$ , i.e. $a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)$
Interpretation	$┌ x ┐$ is a game which will certainly result in outcome $x \in X$ . $┌ 0 ┐$ is a game where White wins and $┌ 1 ┐$ is a game where Black wins. $┌ ϕ \land ψ ┐$ is a game where White can choose to play $ϕ$ or to play $ψ$ . $┌ ϕ \lor ψ ┐$ is a game where Black can choose to play $ϕ$ or to play $ψ$ . $┌ ϕ +_{p} ψ ┐$ is a game where $ϕ$ is played with chance $p$ and $ψ$ with chance $1 - p$ .

15 — infrabayesianism

When agents have beliefs about the same environment that they're embedded in, weird things can happen. Over the past few years, Vanessa Kosoy and Alex Appell have been exploring a novel flavour of uncertainty — infrabayesian uncertainty — which they claim more fruitfully characterises the belief-states of embedded agents. In particular, it characterises belief-states concerning Newcomb-like environments, where the state of the environment is correlated with the agent's choice under consideration. Their flavour of uncertainty corresponds to the infrabayesian monad $□$ .

Roughly speaking, $□$ is the same as $G$ above except without the $\land$ connective. Consider $(Σ, E)$ the theory of convex semilattices with top and bottom, which is a presentation of the composite monad $P_{f}^{+} \circ Δ \circ (- + 2)$ .^[15] From what I understand, this monad $P_{f}^{+} \circ Δ \circ (- + 2)$ is Kosoy's infrabayesian monad $□$ .^[16] This justifies the claim that infrabayesianism is the flavour of uncertainty that minimally encompasses both possibilistic uncertainty (via the $P_{f}^{+}$ monad), probabilistic uncertainty (via the $Δ$ monad), and reward (via the $(- + {0, 1})$ monad). I think that this motivates infrabayesianism as a characterisation of an agent's belief-state about their environment.

Flavour of uncertainty	infrabayesian
Monad $L (Σ, E, -)$	infrabayesian monad
Signature $Σ$	${\lor, 0, 1} \cup {+_{p} : p \in (0, 1)}$
Axioms $E$	$\lor$ is a semilattice with $a \lor 0 = a$ and $a \lor 1 = 1$ . ${+_{p} : p \in (0, 1)}$ is convex algebra. $+_{p}$ distributes over $\lor$ , i.e. $a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)$
Interpretation	$┌ x ┐$ is an environment which certainly results in outcome $x \in X$ . $0$ is an impossible/contradictory environment where the agent achieves no disutility, called Nirvana. $1$ is an environment where the agent suffers maximal disutility. $(ϕ \lor ψ)$ is a environment which is either like $ϕ$ or like $ψ$ , and our agent should be pessimistic here. $(ϕ +_{p} ψ)$ is an environment which is like $ϕ$ with chance $p$ and $ψ$ with chance $1 - p$ .

Unfortunately, $□$ isn't a commutative monad, which means it's not a flavour of uncertainty that you can have to parts of the world, but only to the world in its entirety. Put starkly, there's no way to combine my infrabayesian belief-states about two coin toss to yield a single infrabayesian belief-state about the pair of coin tosses, even when the coin tosses are completely unrelated.^[17] This, I think, limits both the theoretical appeal of infrabayesianism and its tractability.

Theoretically speaking, the fact that $□$ isn't a commutative monad weakens the analogy between infrabayesian uncertainty and possibilistic or probabilistic uncertainty. Many concepts are built upon possibilistic or probabilistic uncertainty which appeal, in an essential way, to the product operators $\otimes^{P +}$ or $\otimes^{Δ}$ . And infrabayesianism, lacking such an operator, is not guaranteed the analogous concept.

Practically speaking, the lack of an infrabayesian product operator is an obstacle to parallelising algorithms which assume infrabayesian belief-states. There is no way to decompose the environment into separate components, discover an infrabayesian belief-state for each component, and then combine those belief-states into a single belief-state about the environment as a whole.

Implications for AI safety

Does this essay have any practical significance, or is it all just abstract nonsense? How does this help us solve the Big Problem? To be perfectly frank, I have no idea. Timelines are probably too short agent foundations, and this essay is maybe agent foundations foundations or something like that. But I feel compelled to offer some practical implications for AI safety to validate my decision to write this essay and your decision to read it.

One lesson is that uncertainty comes in many flavours, and formalisating different flavours of uncertainty isn't mathematically challenging. Just ask yourself the Four C's (Count? Certainty? Collapse? Combine?) and you've got yourself a monad.
Often, you can replace one monad in a formalism with another and everything will still type-check. For example, the stochastic Markov decision processes are transition functions $τ : A \times S \to Δ (O \times S)$ . One can generalise this to $τ : A \times S \to B (O \times S)$ for any monad $B$ we've met so far.
If you're conducting active research into agent foundations, then instead of assuming a fixed flavour of uncertainty (e.g. possibilistic, probabilistic, infrabayesian, etc), perhaps see if you can generalise the theory to an arbitrary monad, or at least an arbitrary commutative monad. I call such theories "parametric in the monad". If you're gonna do foundational work, it often pays to make it highly parametric, even if you only care about a specific case.
1. The theory will be robust to errors about the appropriate flavour of uncertainty.
2. If you want to account for another flavour of uncertainty, you'll have saved yourself time, effort, and ink.
3. You've got more data points to sanity-check the theory — do you get sensible answers when you plug in different monads, e.g. $P_{f}^{+}, id, Δ, □, (- \times [0, 1])$ etc?
If your solution to AI safety involves, at some step, building a formal model of the environment (c.f. Davidad's Open Agency Architecture.) or of a human (c.f. imitative amplification), then this model should carry all the flavours of uncertainty that actually characterise your belief-state about the system. And you shouldn't feel compelled to shoe-horn all your uncertainties into a probability distribution. For example, unless-claused uncertainty seems pretty fundamental — we commit to our stochastic models of the environment and/or a human only within a narrow range of situations — and this flavour of uncertainty seems irreducible to probabilistic uncertainty.

Further questions

In so far as "flavours of uncertainty" is an informal term, there's little we can do to test the correspondence other than enumerating well-known flavours of uncertainty and checking that they do in fact correspond to monads, and vice-versa, enumerating the well-known monads and giving them natural doxastic interpretations. I think my own attempt has been positive, but this result is open to revision.

Secondly, the the biggest asterisks of my essay: my treatment of belief-states has been silent on their most important property, namely that they are learned. For example, a probability distribution can be conditioned on new evidence, and possibilistic uncertainty also carries an analogous notion of conditioning. Perhaps any characterisation of belief should answer additional questions about how those belief-state revised in light of new evidence/observations/considerations, etc. Perhaps we should append to Count? Certainty? Collapse? Combine? a fifth question, Condition? I'm sympathetic to this worry.

And if indeed learning is a phenomenon which must be modelled by any characterisation of belief, then monads do not themselves carry enough structure to characterise beliefs. Rather, we would need to equip the monad $B$ with some additional structure, perhaps a family of maps ${learn}_{S} : O (S) \times B (S) \to B (S)$ for some spce of observations $O (S)$ , possibly satisfying some additional constraints such as ${learn}_{S} (o, -) \circ η_{S} = η_{S}$ and ${learn}_{S} (o_{1} \cdot o_{2}, -) = {learn}_{S} (o_{2}, -) \circ {learn}_{S} (o_{1}, -)$ . I'm just improvising here.

This is best left to future work, if the need arises.

Flavour of uncertainty	Monad
possibilistic	nonempty powerset monad
probabilistic	distribution monad
indeterminate	reader from $H$ monad
confidence-marked	writer to $[0, 1]$ monad
unless-claused	writer to $F$ monad
ordered clarifications	writer to $List (C)$ monad
unordered clarifications	writer to $N [C]$ monad
best guess	identity monad
guess-or-shrug	maybe monad
infinitesimal probabilistic	$LCF$ -distribution monad
generalised probabilistic	$K$ -distribution monad
quantum	quantum monad
evolving	smooth state monad
ex-ante utility	continuation to $R$ monad
utterance in a language	guess-or-many-shrugs
guess-or-different-shrugs	exception monad
path through forking road	full binary trees monad
utterance modulo equivalence	algebraic theory
imprecise probability	convex powerset of distributions monad
ludic	free convex lattice monad
infrabayesian	infrabayesian monad

^{^}
In particular, I'm thinking of the applied category theory community.
^{^}
Traditionally, the field of analytic epistemology has been concerned with defining epistemological concepts — i.e. constructing definitions for the concepts of knowledge, belief, evidence, learning, testimony, justification, etc. However, in recent years analytic epistemology has reorientated itself, chiefly under the influence of Timothy Williamson, towards modelling epistemological phenomena — i.e. constructing mathematical models for phenomena relating knowledge, belief, evidence, learning, testimony, justification, etc. This reorientation in epistemology, from concept-defining to model-building, was inspired by the natural sciences.
^{^}
An operator $F$ assigns, to every set $X$ , another set/function $F (X)$ .
For example, $P$ is the powerset operator, which assigns to every set $X$ another set $P (X)$ . You can informally think of an operator as a function — but strictly speaking, an operator can't be a function because its domain would be the "set of all sets" (which doesn't exist).
Formally, the domain of an operator is something called a category. Categories can be larger than sets — in particular there is a category containing all the sets and the functions between them. For pedagogical purposes, I've framed everything in this article in terms of sets and functions, but most of the content of this article can applied to any category with enough structure.
^{^}
And I suppose, by "generalising backwards", that my zeroth-order belief about the coin toss is the actual result of the coin toss..?
^{^}
$(M, e, ⊙)$ is a monoid if $(a ⊙ b) ⊙ c = a ⊙ (b ⊙ c)$ and $e ⊙ a = a = a ⊙ e$ .
A monoid is like a group except the elements might not have inverses, e.g. $(Z, 0, +)$ is a group but $(N, 0, +)$ is only a monoid.
$(M, e, ⊙)$ is a commutative monoid if also $a ⊙ b = b ⊙ a$ .
The writer monad for $(M, e, ⊙)$ is given by the data $B (X) = X \times M$ , $η_{X}^{B} (x) = (x, e)$ , and $x ⊳_{X Y}^{B} f = (y, a ⊙ b)$ where $x = (x, a)$ and $f (x) = (y, b)$ .
^{^}
Solution: I think $B (X)$ is the $X$ -dimensional hilbert space, but this isn't my expertise.
^{^}
Suppose $R$ has two distinct elements $r_{1}$ and $r_{2}$ . Let $a = λ^{v : A \to R} . r_{1} \in K (A, R)$ and $b = λ^{v : B \to R} . r_{2} \in K (B, R)$ . Then there are two ways to combine $a$ and $b$ into a single belief in $K (A \times B, R)$ , i.e. $λ^{v : A \times B \to R} . r_{1} \in K (A \times B, R)$ and $λ^{v : A \times B \to R} . r_{2} \in K (A \times B, R)$ . But these differ so $K (-, R)$ is not a commutative monad for $| R | \geq 2$ .
^{^}
In fact, $K (-, R)$ encompasses every other monad $T$ such that $α : T (R) \to R$ is a $T$ -algebra. This explains why $K (-, R)$ encompasses both possibilistic and probabilistic uncertainty — specifically, it's because $min : P^{+} (R) \to R$ is a $P^{+}$ -algebra and $E : Δ (R) \to R$ is a $Δ$ -algebra.
Moreover, $K (-, R)$ is the smallest monad with this property, because there's a bijection between $T$ -algebras $α : T (R) \to R$ and monad morphisms $T \Rightarrow K (-, R)$ . See here for details.
That being said, $K (-, R)$ isn't the smallest monad encompassing both $P^{+}$ and $Δ$ in particular. If you only need to encompass $P^{+}$ and $Δ$ then Vanessa Kosoy's infrabayesian monad $□$ will suffice, but $□$ is strictly contained within $K (-, R)$ .
^{^}
For example, suppose $w = ┌ ((w_{1} \lor w_{2}) \land \neg w_{2}) ┐ \in L (Σ, W)$ and $f : W \to L (Σ, S)$ satisfies $f (w_{1}) = ┌ (s_{3} \to \neg s_{1}) ┐$ and $f (w_{2}) = ┌ \neg s_{5} ┐$ . Then we find $s$ via uniform substitution.
$\begin{matrix} s & = w ⊳_{W S} f = ┌ ((f (w_{1}) \lor f (w_{2})) \land \neg f (w_{2}) ┐ = ┌ (((s_{3} \to \neg s_{1}) \lor \neg s_{5}) \land \neg \neg s_{5}) ┐ \in L (Σ, S) \end{matrix}$
In pythonese, S_string = ''.join(t if t in Sigma else f(t) for t in W_string)
Equivalently, we can define the bind operator recursively on the depth of $w$ . For atomic sentences, $┌ w ┐ ⊳_{W S} f = ┌ f (w) ┐$ , and for compound sentences, $┌ σ (ϕ_{1}, \dots, ϕ_{n}) ┐ ⊳_{W S} f = ┌ σ (f (ϕ_{1}), \dots, f (ϕ_{k})) ┐$ .
^{^}
In particular, suppose $Σ = {\neg,!}$ contains two unary connectives. Suppose $a = ┌ \neg a ┐ \in L (Σ, A)$ is my belief-state about $A$ and $b = ┌! b ┐ \in L (Σ, B)$ is my belief-state about $B$ . Then there are two ways to combine these two beliefs into a single belief in $L (Σ, A \times B)$ , i.e. $┌ \neg! ⟨ a, b ⟩ ┐$ and $┌! \neg ⟨ a, b ⟩ ┐$ . But these differ so $L (Σ, -)$ is not a commutative monad.
^{^}
Note that a monad might have many distinct presentations, and this non-uniqueness is rather distasteful. The more elegant treatment of monads is with Lawvere theories, where both atomic connectives and compound connectives are treated on par.
^{^}
For any cardinality $κ$ , we say that a monad has rank $κ$ if it has a presentation with operations of arity at most $κ$ . The continuation monad has no rank (not even an infinitary one) which is a somewhat perverse property for a monad. A rankless monad isn't generated by any algebraic theory, even if we allow infinitary operators.
We can see that $K (-, R)$ is rankless monad because it contains $P$ as a submonad for every $| R | \geq 2$ , but $P$ is a monad without rank.
^{^}
The lattice axioms for the signature $(\lor, \land, 0, 1)$ consists of the semilattice axioms for $\lor$ , the semilattice axioms for $\land$ , the boundary axioms $a \lor 0 = a$ and $a \land 1 = a$ , and the absorption laws $a \lor (a \land b) = a$ and $a \land (a \lor b) = a$ .
^{^}
The position evaluation function $V : G ([0, 1]) \to [0, 1]$ is defined inductively:
$V (┌ r ┐) = r$
$V (┌ 0 ┐) = 0$
$V (┌ 1 ┐) = 1$
$V (┌ ϕ_{1} \lor ϕ_{2} ┐) = max {V (┌ ϕ_{1} ┐), V (┌ ϕ_{2} ┐)}$
$V (┌ ϕ_{1} \land ϕ_{2} ┐) = min {V (┌ ϕ_{1} ┐), V (┌ ϕ_{2} ┐)}$ $V (┌ ϕ_{1} +_{p} ϕ_{2} ┐) = p \cdot V (┌ ϕ_{1} ┐) + (1 - p) \cdot V (┌ ϕ_{2} ┐)$
^{^}
That is, the signature $Σ$ consists of the connectives ${\lor, 0, 1} \cup {+_{p} : p \in (0, 1)}$ , and $E$ contains the axioms: $a \lor a = a$ , $a \lor b = b \lor a$ , $a \lor (b \lor c) = (a \lor b) \lor c$ , $a \lor 0 = a$ , $a \lor 1 = 1$ , $a +_{p} (b \lor c) = (a +_{p} b) \lor (a +_{p} c)$ .
Strictly speaking, it's improper to speak of composing monads $S$ and $T$ unless you provide a distributive law of $S$ over $T$ , i.e. $λ : S \circ T \to T \circ S$ . But $P \circ Δ$ yields a monad $C$ given by the convex powerset of distributions monad, and the exception monad $(- + A)$ distributes over any monad, so no worries here.
^{^}
A technical caveat:
Kosoy's infrabayesian monad $□$ is actually given by $P^{+} \circ Δ \circ (- + 2)$ rather than $P_{f}^{+} \circ Δ \circ (- + 2)$ — that is, $□$ contains sets of distributions with arbitrary cardinality. A least, this is my reading from Diffractor's Infra-Miscellanea Section 2.
Unfortunately, $□$ is a rankless monad, i.e. it isn't generated by any algebraic theory even if we allow infinitary operators.
Fortunately, we may approximate $□$ with a monad of rank $κ$ for any cardinality $κ$ . Let's define $□_{κ} := P_{κ}^{+} \circ Δ \circ (- + 2)$ , where $P_{κ}^{+} (X)$ is the set of non-empty subsets of $X$ of cardinality no greater than $κ$ . Algebraically, we obtain $□_{κ}$ by adding the $κ$ -ary disjunction connective $⋁_{κ}$ to the signature for $Δ \circ (- + 2)$ .
This leaves the open question, for which cardinality $κ$ is $□_{κ}$ an adequate and tractable approximation, if indeed any? I suspect $κ = 2^{ℵ_{0}}$ suffices for all theoretical purposes, and that $κ = 2$ suffices for all practical purposes.
^{^}
This also applies to imprecise probability $C$ and to strategic uncertainty $G$ .
For example, given a series of two-player games $g_{1}, \dots, g_{n} \in G ([0, 1])$ , there's no natural way to combine them into a single two-player game $g_{1} \otimes \dots \otimes g_{n} \in G ([0, 1]^{n})$ because $G$ isn't a commutative monad.
More generally, there's no commutative monad which contains both a $\lor$ operator and a $+_{0.5}$ operator without conflating them. See here for details.

11

Uncertainty in all its flavours

11