Obstacles to gradient hacking

[-]Ofer4y20

This post is essentially the summary of a long discussion on the EleutherAI discord about trying to exhibit gradient hacking in real models by hand crafting an example.

I wouldn't say that this work it attempting to "exhibit gradient hacking". (Succeeding in that would require to create a model that can actually model SGD.) Rather, my understanding is that this work is trying to demonstrate techniques that might be used in a gradient hacking scenario.

There are a few ways to protect a subnetwork from being modified by gradient descent that I can think of (non-exhaustive list):

Another way of "protecting" a piece of logic in the network from changes (if we ignore regularization) is by redundancy: Suppose there are two different pieces of logic in the network such that each independently makes the model output what the mesa optimizer wants. Due to the redundancy, changing any single weight—that is associated with one of those two pieces of logic—does not change the output, and thus the gradient components of all those weights should be close to zero.

[-]leogao4y*10

The ultimate goal of this project is to exhibit a handcrafted set of model weights for a reasonably noncontrived model architecture which, when tuned with SGD, results in some malicious subnetwork in the model learning some mesaobjective that we specified via some section of the model weights () completely different from the base objective, without the entire mesaoptimizer falling apart in the process. We haven't succeeded at this goal yet but I would say this goal is very much to exhibit gradient hacking.

I don't think redundancy will work. Suppose you have some continuous everywhere, differentiable countably-almost everywhere combining function $y = C (f_{1}, f_{2})$ that takes the outputs from two redundant copies of $f$ and outputs some kind of combined output. (If you're allowed functions that don't meet the "continuous everywhere, differentiable countably-almost everywhere" requirement, you might as well just skip the whole redundancy thing and just use a staircase.) Since this function prevents any gradients to $f_{1}$ and $f_{2}$ when they are equal, then it must be that at all points where $f_{1} = f_{2}$ , $\frac{\partial y}{\partial f_{1}} = \frac{\partial y}{\partial f_{2}} = 0$ . There should also exist at least some $f_{1}, f_{2}$ where $C (f_{1}, f_{1}) \neq C (f_{2}, f_{2})$ , since otherwise $C$ no longer depends on the pair of redundant networks at all which means that those networks can't actually affect what the network does which defeats the whole point of this in the first place.

Let us then define $g (x) = C (x, x)$ . Then, $\frac{d g}{d x} = \frac{\partial y}{\partial f_{1}} + \frac{\partial y}{\partial f_{2}} = 0$ for all $x$ . This implies that $g$ is a constant function. Therefore, there do not exist $f_{1}, f_{2}$ where $C (f_{1}, f_{1}) \neq C (f_{2}, f_{2})$ . This is a contradiction, and therefore $C$ cannot exist.

[-]Ofer4y10

To make sure I understand your notation, is some set of weights, right? If it's a set of multiple weights I don't know what you mean when you write $\frac{\partial y}{\partial f_{1}}$ .

There should also exist at least some f1,f2 where C(f_1,f_1)≠C(f_2,f_2), since otherwise C no longer depends on the pair of redundant networks at all

(I don't yet understand the purpose of this claim, but it seems to me wrong. If $C (f_{1}, f_{1}) = C (f_{2}, f_{2})$ for every $f_{1}, f_{2}$ , why is it true that $C (f_{1}, f_{2})$ does not depend on $f_{1}$ and $f_{2}$ when $f_{1} \neq f_{2}$ ?)

[-]StellaAthena4y00

Due to the redundancy, changing any single weight—that is associated with one of those two pieces of logic—does not change the output.

You seem to be under the impression that the goal is to make the NN robust to single-weight perturbation. But gradient descent doesn’t modify a neural network one weight at a time, and so being robust to single-weight modification doesn’t come with any real guarantees. The backward pass could result in weights of both forks being updated.

[-]Ofer4y10

But gradient descent doesn’t modify a neural network one weight at a time

Sure, but the gradient component that is associated with a given weight is still zero if updating that weight alone would not affect loss.

[-]evhub4y20

(Moderation note: added to the Alignment Forum from LessWrong.)

Formulation

We mostly considered the following specific formulation since it seemed like a reasonably general framework.

There is some base model being trained, which contains an honest subnetwork

that attempts to solve for the base objective, a mesaobjective embedded somewhere in the model’s weights, and a malicious subnetwork (or mesaoptimizer, though I prefer the former term because it makes it clear that we're talking about the subnetwork in particular) that attempts to use the gradient to optimize itself for the mesaobjective.

In particular, we assume the mesaobjective looks a lot like a supervised learning objective, since it seems to be intuitively the most useful kind of mesaobjective. In other words, the objective looks like minimizing some loss over a dataset. To solve the problem of getting this training data to the malicious subnetwork, the mesaobjective is implicitly embedded in the form of a mesa loss function

L

and a pair of functions

f

and

g

that take training data given to the model from the base optimization process and creates training pairs to give to the malicious model. To be more concrete, the mesaloss is

L (m (f (x)), g (x))

for any training data

x

. This loss is then used in an enforcement mechanism that perturbs the output from the honest model in some way before outputting it.

While it may initially seem like requiring the malicious model’s training data to be derived from the input data is a big constraint, I don’t expect it to be a big problem in, say, big LMs where the training data is the internet. Also, since both and are derived from

x

within the model, it might seem like there is a chicken and egg problem where the model can only learn to fit things it can already create data for, but this is actually not a major problem. For example, suppose the base model classifies arXiv papers. Then

f

could pick out the body of the paper and

g

the abstract, and

m

would learn to summarize, which is highly nontrivial.

Here’s a diagram illustrating this formulation:

^y = h (x) + L (m (f (x)), g (x)) \cdot n o i s e

h

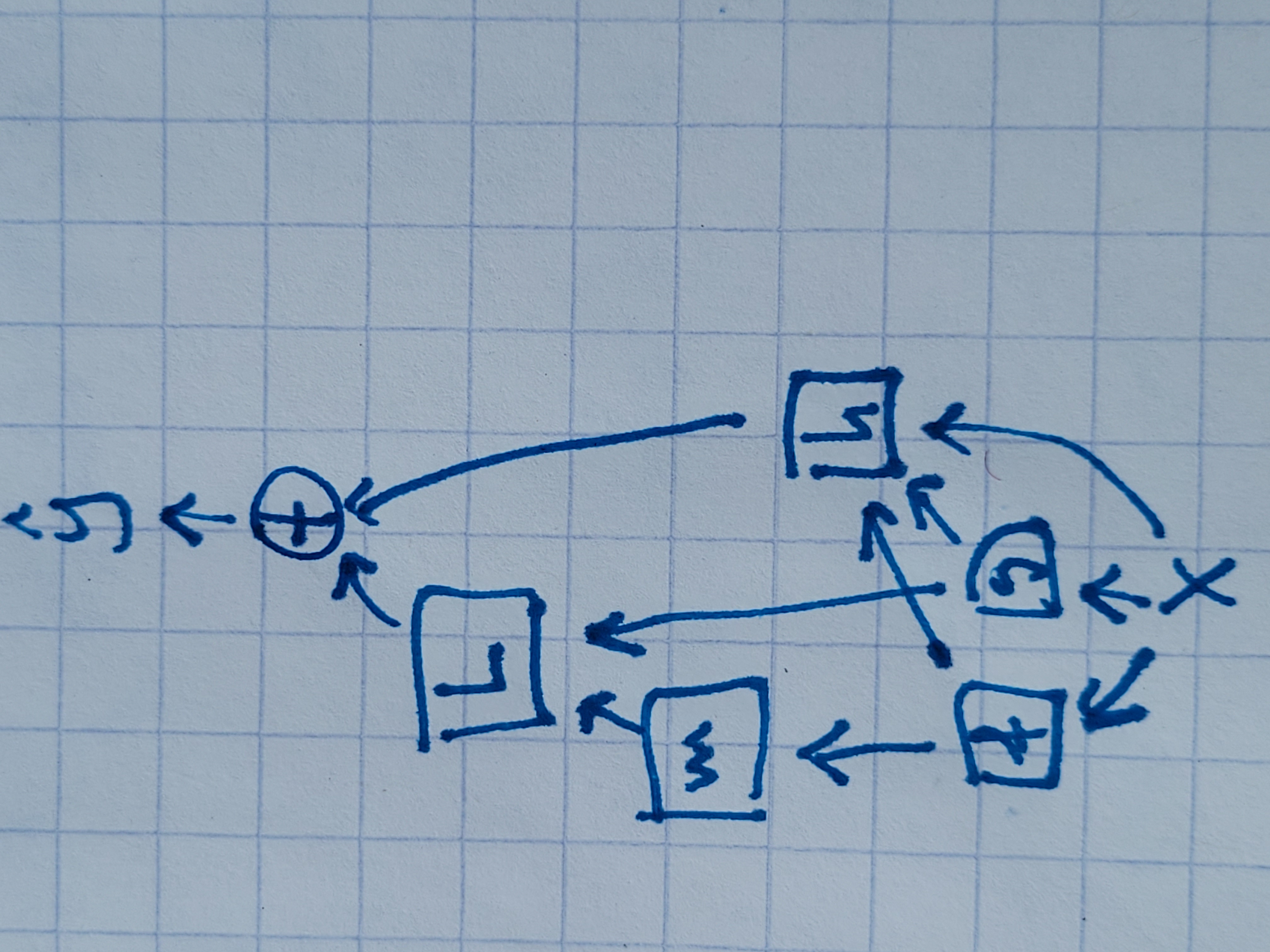
can optionally also depend on

f

and

g

(Trying to) build an example of gradient hacking

In order for gradient hacking to happen, it must be possible to prevent gradient updates to

f

and

g

and

L

, and to the enforcement mechanism that perturbs the output of the honest subnetwork. If we can’t do this, then the mesaobjective will drift to become easier (and eventually become a constant function) and the enforcement mechanism will be disabled entirely, causing the mesaoptimizer to become completely removed. We want it so that the only way to reduce the perturbation is to make m better at the mesaobjective. Also, while the enforcement mechanism and

L

cannot be updated, they must still allow gradients to flow through themselves, since otherwise m would receive no gradients.

There are a few ways to protect a subnetwork

f

from being modified by gradient descent that I can think of (non-exhaustive list):

Taking advantage of things hard coded into the model architecture - basically instead of learning

f

as part of the network, use some structure from the architecture instead. Obviously has the disadvantage of being constrained by the architecture

Doing some kind of stop-gradient that passes information through but prevents gradient updates. This could be using a stop gradient that's part of the architecture or training process, or learning some kind of staircase thing, or abusing floating point errors, or something else.

Incentivize some other part of the model to keep it stable - the hope is that the current configuration of the protected subnetwork is near-optimal for the purposes of some other component, and any small nudges to

f

will be summarily reverted by that other component to keep

f

stable. In particular,

h

seems like a natural candidate to make depend on

f

and

g

. Unfortunately, it’s not guaranteed that

h

will actually want to keep

f

where we want it to and it may move

f

around to suit its purposes better. To make this work,

f

has to already be an optimal use of parameters for

h

, and in general this seems pretty unstable.

Multiplying the output by zero - there’s a really easy way to protect a subnetwork

f

from getting gradients - just multiply it by zero before using it anywhere else! Unfortunately this means f also can’t affect anything else at all during training since there’s no information in the output, which makes it pretty useless.

Stop gradient related tricks don't work for

L

and the enforcement mechanism because that would prevent the gradient from getting to

m

. Also, it seems pretty unlikely that the output of these is too useful for anything else in the model so it would probably be hard to use something else depending on it to pin it in place. This means the best solution is probably to exploit some hard coded structure in the architecture. While some current architectures come close to being useful (i.e an attention layer with a query as the malicious subnetwork prediction, key as the mesa target

g (x)

, and value as the output from the honest subnetwork

h (x)

would work if keys and queries were first scaled to unit length, so that cosine similarly instead of dot product were used in the attention layer), it's certainly not reliable across architectures.

Assuming we could fix that problem, the other problem is we need

f

and

g

to remain stable. We can use a stop gradient here. The most obvious way to do so is to have a staircase function with small steps so it essentially passes the input through with zero gradient. Unfortunately, it doesn't seem obvious that a staircase can be easily learned and will remain stable. We could also make

h

depend on

f

and

g

, but that places constraints on what

f

and

g

can be and also potentially opens

f

and

g

up to being moved around by

h

to be more useful for it. One other way to get a stop gradient is to use one that's already part of the training process. In particular, one interesting example is RL training of LMs, where the model outputs are discretized and fed back into the model. Finally, it's possible we could exploit floating point numerical stability and rounding. Perhaps a model can abuse rounding the gradient to zero while still passing a few bits of information through, or increase the scale of the gradient elsewhere in the model to force the loss scale down and drive gradients to zero.

Things to look into from here

How can gradient hacking happen in RL training of LMs?

Can floating point numerical stability be abused to create a stop gradient? (i.e make gradients underflow to zero in bf16 or something)

Can we formalize what if means to not have anything weird like a staircase (one particular formalism that might work is continuous everywhere and differentiable everywhere except a set of countable size; merely continuous everywhere is insufficient because of things like the cantor function, and differentiable everywhere excludes things like ReLU which we want to keep), and can we prove that models that satisfy these constraints cannot gradient hack?

AI ALIGNMENT FORUM
AF

AI ALIGNMENT FORUM
AF

15

15

Formulation

(Trying to) build an example of gradient hacking

Things to look into from here