Theorem 6: Causal IPOMDP's: Any infra-POMDP with transition kernel $K : S \times A i k \to O \times S$ which fulfills the niceness conditions and always produces crisp infradistributions, and starting infradistribution $ψ \in □ S$ , produces a causal belief function via $Θ (π) := p r_{(A \times O)^{ω} *} (ψ ⋉ K_{: \infty}^{π})$ .

So, first up, we can appeal to Theorem 4 on Pseudocausal IPOMDP's, to conclude that all the $K_{: \infty}^{π}$ are well-defined, and that this $Θ$ we defined fulfills all belief function conditions except maybe normalization.

The only things to check are that the resulting $Θ$ is normalized, and that the resulting $Θ$ is causal. The second is far more difficult and makes up the bulk of the proof, so we'll just dispose of the first one.

T6.1 First, $K$ , since it's crisp by assumption, always has $K (s, a) (c) = c$ for all constants $c$ . The same property extends to all the $K_{n}^{π}$ (they're all crisp too) and then from there to $K_{: \infty}^{π}$ by induction. Then we can just use the following argument, where $π$ is arbitrary.

$Θ (π) (1) = p r_{(A \times O)^{ω} *} (ψ ⋉ K_{: \infty}^{π}) (1) = (ψ ⋉ K_{: \infty}^{π}) (1) = ψ (λ s_{0} . K_{: \infty}^{π} (s_{0}) (1)) = ψ (1) = 1$

The last two inequalities were by $K_{: \infty}^{π}$ mapping constants to the same constant regardless of $π$ , and by $ψ$ being normalized since it's an infradistribution. This same proof works if you swap out the 1 with a 0, so we have normalization for $Θ$ .

T6.2 All that remains is checking the causality condition. We'll be using the alternate rephrasing of causality. We have $Θ$ defined as

$Θ (π^{'}) := p r_{(A \times O)^{ω} *} (ψ ⋉ K_{: \infty}^{π^{'}})$

and want to derive our rephrasing of causality, that for any $U$ and $π^{'}$ and $ζ$ and family $U_{π}$ , we have

$(\forall e : U (π^{'} \cdot e) \geq E_{π \sim ζ} [U_{π} (π \cdot e)]) \to Θ (π^{'}) (U) \geq E_{π \sim ζ} [Θ (π) (U_{π})]$

Accordingly, we get to fix a $U, π^{'}, ζ$ , and family of functions $U_{π}$ , and assume

$\forall e : U (π^{'} \cdot e) \geq E_{π \sim ζ} [U_{π} (π \cdot e)]$

Our proof target is

$Θ (π^{'}) (U) \geq E_{π \sim ζ} [Θ (π) (U_{π})]$

Applying our reexpression of $Θ$ in terms of $ψ$ and $K_{: \infty}^{π}$ and projection, we get

$p r_{(A \times O)^{ω} *} (ψ ⋉ K_{: \infty}^{π^{'}}) (λ a o_{1 : \infty} . U (a o_{1 : \infty})) \geq E_{π \sim ζ} [p r_{(A \times O)^{ω} *} (ψ ⋉ K_{: \infty}^{π}) (λ a o_{1 : \infty} . U_{π} (a o_{1 : \infty}))]$

Undoing the projections on both sides, we get

$(ψ ⋉ K_{: \infty}^{π^{'}}) (λ s_{0}, a o s_{1 : \infty} . U (a o_{1 : \infty})) \geq E_{π \sim ζ} [(ψ ⋉ K_{: \infty}^{π}) (λ s_{0}, a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))]$

Unpacking the semidirect product, we get

$ψ (λ s_{0} . K_{: \infty}^{π^{'}} (s_{0}) (λ a o s_{1 : \infty} . U (a o_{1 : \infty}))) \geq E_{π \sim ζ} [ψ (λ s_{0} . K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty})))]$

Now, we can notice something interesting here. By concavity for infradistributions, we have

$ψ (λ s_{0} . E_{π \sim ζ} [K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))]) \geq E_{π \sim ζ} [ψ (λ s_{0} . K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty})))]$

So, our new proof target becomes

$ψ (λ s_{0} . K_{: \infty}^{π^{'}} (s_{0}) (λ a o s_{1 : \infty} . U (a o_{1 : \infty}))) \geq ψ (λ s_{0} . E_{π \sim ζ} [K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))])$

Because if we hit that, we can stitch the inequalities together. The obvious move to show this new result is to apply monotonicity of infradistributions. If the inner function on the left hand side was always above the inner function on the right hand side, we'd have our result by infradistribution monotonicity. So, our new proof target becomes

$\forall s_{0} : K_{: \infty}^{π^{'}} (s_{0}) (λ a o s_{1 : \infty} . U (a o_{1 : \infty})) \geq E_{π \sim ζ} [K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))]$

At this point, now that we've gotten rid of $ψ$ , we can use the full power of crisp infradistributions. Crisp infradistributions are just a set of probability distributions! Remember that the semidirect product, $ψ ⋉ K$ , can be viewed as taking a probability distribution from $ψ$ , and for each $x$ , picking a conditional probability distribution from $K (x)$ , and all the probability distributions of that form make up $ψ ⋉ K$ .

In particular, the infinitely iterated semidirect product here can be written as a repeated process where, for each history of the form $s_{0}, a o s_{1 : n}, a,$ Murphy gets to select a probability distribution over the next observation and state from $K (s_{n}, a)$ (as a set of probability distributions) to fill in the next part of the action-observation-state tree. Accordingly every single probability distribution in $K_{: \infty}^{π} (s_{0})$ can be written as $π$ interacting with an expanded probabilistic environment $e^{Δ +}$ of type $(A \times O \times S)^{< ω} \times A \to Δ (O \times S)$ (which gives Murphy's choice wherever it needs to pick the next observation and state), subject to the constraints that

$e^{Δ +} (a o s_{1 : n}, a) \in K (s_{n}, a)$

and

$e^{Δ +} (\emptyset, a) \in K (s_{0}, a)$

We'll abbreviate this property that $e^{Δ +}$ always picks stuff from the appropriate $K$ set and starts off picking from $K (s_{0}, a)$ as $e^{Δ +} \sim K, s_{0}$ .

Our old proof goal of

$\forall s_{0} : K_{: \infty}^{π^{'}} (s_{0}) (λ a o s_{1 : \infty} . U (a o_{1 : \infty})) \geq E_{π \sim ζ} [K_{: \infty}^{π} (s_{0}) (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))]$

can be rephrased as

$\forall s_{0} : {inf}_{μ^{'} \in K_{: \infty}^{π^{'}} (s_{0})} μ^{'} (λ a o s_{1 : \infty} . U (a o_{1 : \infty})) \geq E_{π \sim ζ} [{inf}_{μ_{π} \in K_{: \infty}^{π} (s_{0})} μ_{π} (λ a o s_{1 : \infty} . U_{π} (a o_{1 : \infty}))]$

and then rephrased as

$\forall s_{0} : {inf}_{μ^{'} \in K_{: \infty}^{π^{'}} (s_{0})} E_{a o s_{1 : \infty} \sim μ^{'}} [U (a o_{1 : \infty})] \geq E_{π \sim ζ} [{inf}_{μ_{π} \in K_{: \infty}^{π} (s_{0})} E_{a o s_{1 : \infty} \sim μ_{π}} [U_{π} (a o_{1 : \infty})]]$

And now, by our earlier discussion, we can rephrase this statement in terms of picking expanded probabilistic environments.

$\forall s_{0} : {inf}_{e^{Δ^{'} +} \sim K, s_{0}} E_{a o s_{1 : \infty} \sim π^{'} \cdot e^{Δ^{'} +}} [U (a o_{1 : \infty})] \geq E_{π \sim ζ} [{inf}_{e_{π}^{Δ +} \sim K, s_{0}} E_{a o s_{1 : \infty} \sim π \cdot e_{π}^{Δ +}} [U_{π} (a o_{1 : \infty})]]$

Now, on the right side, since the set we're selecting the expanded environments from is the same each time and doesn't depend on $π$ , we can freely move the inf outside of the expectation. It is unconditionally true that

${inf}_{e^{Δ +} \sim K, s_{0}} E_{π \sim ζ} [E_{a o s_{1 : \infty} \sim π \cdot e^{Δ +}} [U_{π} (a o_{1 : \infty})]] \geq E_{π \sim ζ} [{inf}_{e_{π}^{Δ +} \sim K, s_{0}} E_{a o s_{1 : \infty} \sim π \cdot e_{π}^{Δ +}} [U_{π} (a o_{1 : \infty})]]$

So now, our proof goal shifts to

$\forall s_{0} : {inf}_{e^{Δ^{'} +} \sim K, s_{0}} E_{a o s_{1 : \infty} \sim π^{'} \cdot e^{Δ^{'} +}} [U (a o_{1 : \infty})] \geq {inf}_{e^{Δ +} \sim K, s_{0}} E_{π \sim ζ} [E_{a o s_{1 : \infty} \sim π \cdot e^{Δ +}} [U_{π} (a o_{1 : \infty})]]$

because if that were true, we could pair it up with the always-true inequality to hit our old proof goal. And we'd be able to show this proof goal if we showed the following, more ambitious result.

$\forall e^{Δ +} : E_{a o s_{1 : \infty} \sim π^{'} \cdot e^{Δ +}} [U (a o_{1 : \infty})] \geq E_{π \sim ζ} [E_{a o s_{1 : \infty} \sim π \cdot e^{Δ +}} [U_{π} (a o_{1 : \infty})]]$

Note that we're not restricting to compatibility with $K$ and $s_{0}$ , we're trying to show it for any expanded probabilistic environment of type $(A \times O \times S)^{< ω} \times A \to Δ (O \times S)$ . We can rephrase this new proof goal slightly, viewing ourselves as selecting an action and observation history.

$\forall e^{Δ +} : E_{a o_{1 : \infty} \sim p r_{(A \times O)^{ω} *} (π^{'} \cdot e^{Δ +})} [U (a o_{1 : \infty})] \geq E_{π \sim ζ} [E_{a o_{1 : \infty} \sim p r_{(A \times O)^{ω} *} (π \cdot e^{Δ +})} [U_{π} (a o_{1 : \infty})]]$

Now, for any expanded probabilistic environment $e^{Δ +} : (A \times O \times S)^{< ω} \times A \to Δ (O \times S)$ , there is a unique corresponding probabilistic environment $e^{Δ}$ of type $(A \times O)^{< ω} \times A \to Δ O$ where, for any policy, $p r_{(A \times O)^{ω} *} (π \cdot e^{Δ +}) = π \cdot e^{Δ}$ . This is just the classical result that any POMDP can be viewed as a MDP with a state space consisting of finite histories, it still behaves the same. Using this swap, our new proof goal is:

$\forall e^{Δ} : E_{a o_{1 : \infty} \sim π^{'} \cdot e^{Δ}} [U (a o_{1 : \infty})] \geq E_{π \sim ζ} [E_{a o_{1 : \infty} \sim π \cdot e^{Δ}} [U_{π} (a o_{1 : \infty})]]$

Where $e^{Δ}$ is an arbitrary probabilistic environment. Now, you can take any probabilistic environment $e^{Δ}$ and view it as a mixture of deterministic environments $e$ . So we can rephrase $e^{Δ}$ as, at the start of time, picking a $e$ from $ξ \in Δ E$ for some particular $ξ$ . This is our mixture of deterministic environments that makes up $e^{Δ}$ . This mixture isn't necessarily unique, but there's always some mixture of deterministic enivironments that works to make $e^{Δ}$ where $e^{Δ}$ is arbitrary. So, our new proof goal becomes:

$\forall ξ \in Δ E : E_{e \sim ξ} [E_{a o_{1 : \infty} \sim π^{'} \cdot e} [U (a o_{1 : \infty})]] \geq E_{π \sim ζ} [E_{e \sim ξ} [E_{a o_{1 : \infty} \sim π \cdot e} [U_{π} (a o_{1 : \infty})]]]$

Since $π \cdot e$ is just a dirac-delta distribution on a particular history, we can substitute that in to get the equivalent

$\forall ξ \in Δ E : E_{e \sim ξ} [U (π^{'} \cdot e)] \geq E_{π \sim ζ} [E_{e \sim ξ} [U_{π} (π \cdot e)]]$

Now we just swap the two expectations.

$\forall ξ \in Δ E : E_{e \sim ξ} [U (π^{'} \cdot e)] \geq E_{e \sim ξ} [E_{π \sim ζ} [U_{π} (π \cdot e)]]$

And then we remember that our starting assumption was

$\forall e : U (π^{'} \cdot e) \geq E_{π \sim ζ} [U_{π} (π \cdot e)]$

So we've managed to hit our proof target and we're done, this propagates back to show causality for $Θ$ .

Theorem 7: Pseudocausal to Causal Translation: The following diagram commutes when the bottom belief function $Θ$ is pseudocausal. The upwards arrows are the causal translation procedures, and the top arrows are the usual morphisms between the type signatures. The new belief function $Θ^{c}$ is causal. Also, if $U : (A \times O)^{ω} \to [0, 1]$ , and $U^{N} : (A \times (O + N))^{ω} \to [0, 1]$ is defined as $1$ for any history containing Nirvana, and $U (h)$ for any nirvana-free history, then $\forall π : Θ^{c} (π) (U^{N}) = Θ (π) (U)$ .

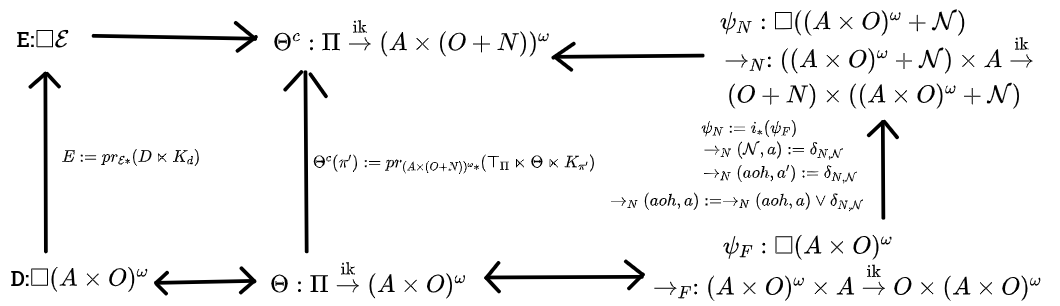
T7.0 Preliminaries. Let's restate what the translations are. The notation $d (e, h)$ is that $e$ "defends" $h$ . $e$ defends $h$ if it responds to any prefix of $h$ which ends in an action with either the next observation in $h$ , or Nirvana, and responds to any non-prefixes of $h$ with Nirvana.

Also, we'll write $h^{N} \sim π^{'}, h$ if $h^{N}$ is "compatible" with $π^{'}$ and $h$ . The criterion for this is that $h^{N} \sim π^{'}$ , and that any prefix of $h^{N}$ which ends in an action and contains no Nirvana observations must either be a prefix of $h$ , or only deviate from $h$ in the last action. An alternate way to state that is that $h^{N}$ is capable of being produced by a copolicy which defends $h$ , interacting with $π^{'}$ .

With these two notes, we introduce the infrakernels $K_{d} : (A \times O)^{ω} i k \to E$ , and $K_{π^{'}} : (A \times O)^{ω} i k \to (A \times (O + N))^{ω}$ .

$K_{d} (h)$ is total uncertainty over $e$ such that $e$ defends $h$ . $K_{d} (h) (f) := {inf}_{e : d (e, h)} f (e)$

And $K_{π^{'}} (h)$ is total uncertainty over $h^{N}$ such that $h^{N}$ is compatible with $π^{'}$ and $h$ . $K_{π^{'}} (h) (U^{N}) := {inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N})$

Now, to briefly recap the three translations.For first-person static translation, we have

$Θ^{c} (π^{'}) := p r_{(A \times (O + N))^{ω} *} (⊤_{Π} ⋉ Θ ⋉ K_{π^{'}})$

Where $Θ$ is the original belief function.

For third-person static translation, we have

$E := p r_{E *} (D ⋉ K_{d})$

Where $D$ is the original infradistribution over $(A \times O)^{ω}$ .

For first-person dynamic translation, the new infrakernel has type signature

$((A \times O)^{ω} + N) \times A i k \to ((O + N) \times ((A \times O)^{ω} + N))$

Ie, the state space is destinies plus a single Nirvana state, and the observation state is the old space of observations plus a Nirvana observation. $N$ is used for the Nirvana observation, and $N$ is used for the Nirvana state. The transition dynamics are:

$\forall a^{'} \in A : \to_{N} (N, a^{'}) := δ_{N, N}$

and, if $a^{'} \neq a$ , then $\to_{N} (a o h, a^{'}) := δ_{N, N}$

and otherwise, $\to_{N} (a o h, a) := δ_{o, h} \lor δ_{N, N}$

The initial infradistribution is $i_{*} (ψ_{F})$ , the obvious injection of $ψ_{F}$ from $(A \times O)^{ω}$ to $(A \times O)^{ω} + N$ .

The obvious way to show this theorem is that we can assume the bottom part of the diagram commutes and $ψ_{F}, Θ, D$ are all pseudocausal, and then show that all three paths to $Θ^{c}$ produce the same result, and it's causal. Then we just wrap up that last part about the utility functions.

Fortunately, assuming all three paths produce the same $Θ^{c}$ belief function, it's trivial to show that it's causal. $i_{*} (ψ_{F})$ is an infradistribution since $ψ_{F}$ is, and $\to_{N}$ is a crisp infrakernel, so we can just invoke Theorem 6 that crisp infrakernels produce causal belief functions to show causality for $Θ^{c}$ . So we only have to check that all three paths produce the same result, and show the result about the utility functions. Rephrasing one of the proofs is one phase, and then there are two more phases showing that the other two phases hit the same target, and the last phase showing our result about the utility functions.

We want to show that

$Θ^{c} (π^{'}) = (π^{'} \cdot)_{*} (E) = p r_{(A \times (O + N))^{ω} *} (i_{*} (ψ_{F}) ⋉ \to_{N : \infty}^{π^{'}})$

T7.1 First, let's try to rephrase $Θ^{c} (π^{'}) (U^{N})$ into a more handy form for future use. Invoking our definition of $Θ^{c} (π^{'})$ , we have:

$Θ^{c} (π^{'}) (U^{N}) = p r_{(A \times (O + N))^{ω} *} (⊤_{Π} ⋉ Θ ⋉ K_{π^{'}}) (U^{N})$

Then, we undo the projection

$= (⊤_{Π} ⋉ Θ ⋉ K_{π^{'}}) (λ π, h, h^{N} . U^{N} (h^{N}))$

And unpack the semidirect product

$= ⊤_{Π} (λ π . Θ (π) (λ h . K_{π^{'}} (h) (λ h^{N} . U^{N} (h^{N}))))$

And unpack what $⊤_{Π}$ means

$= {inf}_{π} Θ (π) (λ h . K_{π^{'}} (h) (λ h^{N} . U^{N} (h^{N})))$

And then apply the definition of $K_{π^{'}} (h)$

$= {inf}_{π} Θ (π) (λ h . {inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N}))$

This will be our final rephrasing of $Θ^{c} (π^{'}) (U^{N})$ . Our job is to derive this result for the other two paths.

T7.2 First up, the third-person static translation. We can start with definitions.

$(π^{'} \cdot)_{*} (E) (U^{N}) = (π^{'} \cdot)_{*} (p r_{E *} (D ⋉ K_{d})) (U^{N})$

And then, we can recall that since $D$ and $Θ$ are assumed to commute, we can define $D$ in terms of $Θ$ via $D = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)$ . Making this substitution, we get

$= (π^{'} \cdot)_{*} (p r_{E *} ((p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) ⋉ K_{d})) (U^{N})$

We undo the first pushforward

$= p r_{E *} ((p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) ⋉ K_{d}) (λ e . U^{N} (π^{'} \cdot e))$

And then the projection

$= ((p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) ⋉ K_{d}) (λ h, e . U^{N} (π^{'} \cdot e))$

And unpack the semidirect product

$= p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ) (λ h . K_{d} (h) (λ e . U^{N} (π^{'} \cdot e)))$

And remove the projection

$= (⊤_{Π} ⋉ Θ) (λ π, h . K_{d} (h) (λ e . U^{N} (π^{'} \cdot e)))$

and unpack the semidirect product and what $⊤_{Π}$ is

$= {inf}_{π} Θ (π) (λ h . K_{d} (h) (λ e . U^{N} (π^{'} \cdot e)))$

Now, we recall that $K_{d} (h)$ is all the $e$ that defend $h$ , to get

$= {inf}_{π} Θ (π) (λ h . {inf}_{e : d (e, h)} U^{N} (π^{'} \cdot e))$

At this point we can realize that for any $e$ which defends $h$ , when $e$ interacts with $π^{'}$ , it makes a $h^{N}$ that is compatible with $π^{'}$ and $h$ . Further, all $h^{N}$ compatible with $π^{'}$ and $h$ have an $e$ which produces them. If $h^{N}$ has its nirvana-free prefix not being a prefix of $h$ , then the defending $e$ which doesn't end $h$ early, just sends deviations to Nirvana, is capable of producing it. If $h^{N}$ looks like $h$ but ended early with Nirvana, you can just have a defending $e$ which ends with Nirvana at the same time. So we can rewrite this as

$= {inf}_{π} Θ (π) (λ h . {inf}_{h^{N} \sim π^{'}, h} : U^{N} (h^{N}))$

And this is exactly the form we got for $Θ (π^{'}) (U^{N})$ .

T7.3 Time for the third and final translation. We want to show that

$p r_{(A \times (O + N))^{ω} *} (i_{*} (ψ_{F}) ⋉ \to_{N : \infty}^{π^{'}}) (U^{N})$

is what we want. Because the pseudocausal square commutes, we have that $ψ^{F} = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)$ , so we can make that substitution to yield

$= p r_{(A \times (O + N))^{ω} *} (i_{*} (p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) ⋉ \to_{N : \infty}^{π^{'}}) (U^{N})$

Remove the projection, to get

$= (i_{*} (p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) ⋉ \to_{N : \infty}^{π^{'}}) (λ s_{0}^{N}, a o s_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N}))$

For this notation, we're using $s^{N}$ to refer to an element of $(A \times O)^{ω} + N$ , the state space. $a o s_{1 : \infty}^{N}$ is an element of $(A \times (O + N) \times ((A \times O)^{ω} + N))^{ω}$ , a full unrolling. $a o_{1 : \infty}^{N}$ is the projection of this to $(A \times (O + N))^{ω}$ .

We unpack the semidirect product to yield

$= i_{*} (p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ)) (λ s_{0}^{N} . \to_{N : \infty}^{π^{'}} (s_{0}^{N}) (λ a o s_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N})))$

and rewrite the injection pushforward

$= p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ) (λ h . \to_{N : \infty}^{π^{'}} (h) (λ a o s_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N})))$

and remove the projection

$= (⊤_{Π} ⋉ Θ) (λ π, h . \to_{N : \infty}^{π^{'}} (h) (λ a o s_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N})))$

And unpack the semidirect product along with $⊤_{Π}$ .

$= {inf}_{π} Θ (π) (λ h . \to_{N : \infty}^{π^{'}} (h) (λ a o s_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N})))$

Now we rewrite this as a projection to yield

$= {inf}_{π} Θ (π) (λ h . p r_{(A \times (O + N))^{ω} *} (\to_{N : \infty}^{π^{'}} (h)) (λ a o_{1 : \infty}^{N} . U^{N} (a o_{1 : \infty}^{N})))$

And do a little bit of reindexing for convenience, swapping out the symbol $a o_{1 : \infty}^{N}$ for $h^{N}$ , getting

$= {inf}_{π} Θ (π) (λ h . p r_{(A \times (O + N))^{ω} *} (\to_{N : \infty}^{π^{'}} (h)) (λ h^{N} . U^{N} (h^{N})))$

And now, we can ask what $p r_{(A \times (O + N))^{ω} *} (\to_{N : \infty}^{π^{'}} (h))$ is. Basically, the starting state is the destiny $h$ , and then $π^{'}$ interacts with it through the kernel $\to_{N}$ . Due to how $\to_{N}$ is defined, it can do one of three things. First, it could just unroll $h$ all the way to completion, if $h$ is the sort of history that's compatible with $π^{'}$ . Second, it could partially unroll $h$ and deviate to Nirvana early, even if $π^{'}$ is compatible with more, because of how $\to_{N} (a o h, a)$ is defined. Finally, $π^{'}$ could deviate from $h$ and then $\to_{N}$ would have to respond with Nirvana. And of course, once you're in a Nirvana state, you're in there for good. Hm, you have total uncertainty over histories $h^{N}$ compatible with $π^{'}$ and $h$ , any of them at all could be made by $p r_{(A \times (O + N))^{ω} *} (\to_{N : \infty}^{π^{'}} (h))$ . So, this projection of the infrakernel unrolling $h$ is just $K_{π^{'}} (h)$ . We get

$= {inf}_{π} Θ (π) (λ h . K_{π^{'}} (h) (λ h^{N} . U^{N} (h^{N})))$

And then we use what $K_{π^{'}} (h)$ does to functions, to get

$= {inf}_{π} Θ (π) (λ h . {inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N}))$

Which is exactly the form we need. So, all three translation procedures produce identical belief functions.

T7.4 The only thing which remains to wrap this result up is guaranteeing that, if $U^{N} : (A \times (O + N))^{ω} \to [0, 1]$ is 1 if the history contains Nirvana, (or infinity for the $R$ type signature), and $U$ otherwise, then $Θ^{c} (π^{'}) (U^{N}) = Θ (π^{'}) (U)$ .

We rephrased $Θ^{c} (π^{'}) (U^{N})$ as ${inf}_{π} Θ (π) (λ h . {inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N}))$

We can notice something interesting. If $h$ is the sort of history that $π^{'}$ is capable of making, ie $h \sim π^{'}$ , then all of the $h^{N} \sim π^{'}, h$ are going to end up in Nirvana except $h$ itself, because all the $h^{N}$ are like "follow $π^{'}$ , any deviations of $π^{'}$ from $h$ go to Nirvana, and also Nirvana can show up early". In this case, since any history ending with Nirvana is maximum utility, and otherwise $U$ is copied, we have ${inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N}) = U (h)$ . However, if $h$ is incompatible with $π^{'}$ , then no matter what, a history $h^{N}$ which follows $π^{'}$ is going to hit Nirvana and be assigned maximum utility. So, we can rewrite

${inf}_{π} Θ (π) (λ h . {inf}_{h^{N} \sim π^{'}, h} U^{N} (h^{N}))$

as

$= {inf}_{π} Θ (π) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

Which can be written as an update, yielding

$= {inf}_{π} u_{\sim π^{'}}^{1} (Θ (π)) (U)$

And then, we remember that regardless of $π^{'}$ and $π$ , for pseudocausal belief functions, which $Θ$ is, we have that $u_{\sim π^{'}}^{1} (Θ (π)) (U) \geq Θ (π^{'}) (U)$ , so the update assigns higher expectation values than $Θ (π^{'})$ does. Also, $u_{\sim π^{'}}^{1} (Θ (π^{'})) = Θ (π^{'})$ . Thus, the infinimum is attained by $π^{'}$ , and we get

$= Θ (π^{'}) (U)$

and we're done.

Theorem 8: Acausal to Pseudocausal Translation: The following diagram commutes when the bottom belief function $Θ$ is acausal. The upwards arrows are the pseudocausal translation procedures, and the top arrows are the usual morphisms between the type signatures. The new belief function $Θ^{p}$ will be pseudocausal.

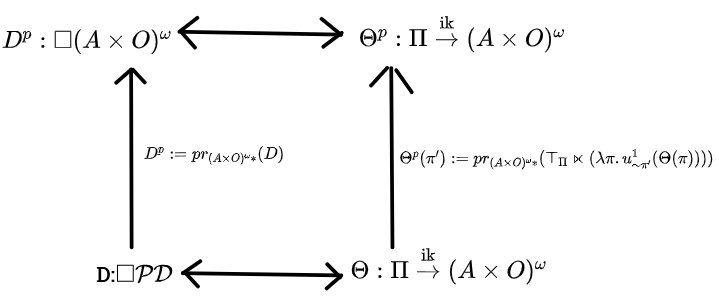
T8.0 First, preliminaries. The two translation procedures are, to go from an infradistribution over policy-tagged destinies $D$ , to an infradistribution over destinies $D^{p}$ , we just project.

$D^{p} := p r_{(A \times O)^{ω} *} (D)$

And, to go from an acausal belief function $Θ$ to a pseudocausal one $Θ^{p}$ , we do the translation

$Θ^{p} (π^{'}) := p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π))))$

We assume that $D$ and $Θ$ commute, and try to show that these translation procedures result in a $Θ^{p}$ and $D^{p}$ which are pseudocausal and commute with each other. So, our proof goals are that

$Θ^{p} (π^{'}) = u_{\sim π^{'}}^{1} (D^{p})$

and

$D^{p} = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ^{p})$

Once we've done that, it's easy to get that $Θ^{p}$ is pseudocausal. This occurs because the projection of any infradistribution is an infradistribution, so we can conclude that $D^{p}$ is an infradistribution over $(A \times O)^{ω}$ . Also, back in the Pseudocausal Commutative Square theorem, we were able to derive that any infradistribution $D^{p}$ over $(A \times O)^{ω}$ , when translated to a $Θ^{p}$ , makes a pseudocausal belief function, no special properties were used in that except being an infradistribution.

T8.1 Let's address the first one, trying to show that

$Θ^{p} (π^{'}) = u_{\sim π^{'}}^{1} (D^{p})$

We'll take the left side, plug in some function, and keep unpacking and rearranging until we get the right side with some function plugged in. First up is applying definitions.

$Θ^{p} (π^{'}) (U) = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))) (U)$

by how $Θ^{p}$ was defined. Now, we start unpacking. First, the projection.

$= (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))) (λ π, h . U (h))$

Then unpack the semidirect product and $⊤_{Π}$ , for

$= {inf}_{π} u_{\sim π^{'}}^{1} (Θ (π)) (λ h . U (h))$

Then unpack the update, to get

$= {inf}_{π} Θ (π) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

Then pack up the ${inf}_{π}$

$= ⊤_{Π} (λ π . Θ (π) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}}))$

And pack up the semidirect product

$= (⊤_{Π} ⋉ Θ) (λ π, h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

And since $D = ⊤_{Π} ⋉ Θ$ for the original acausal belief function, we can rewrite this as

$= D (λ π, h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

And pack this up in a projection.

$= p r_{(A \times O)^{ω} *} (D) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

And then, since we defined $D^{p} := p r_{(A \times O)^{ω} *} (D)$ , we can pack this up as

$= D^{p} (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

And then pack up the update

$= u_{\sim π^{'}}^{1} (D^{p}) (U)$

So, that's one direction done.

T8.2 Now for the second result, showing that

$D^{p} = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ^{p})$

Again, we'll take the more complicated form, and write it as the first one, for arbitrary functions $U$ .bWe begin with

$p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ Θ^{p}) (U)$

and then unpack what $Θ_{p} (π^{'})$ is to get

$= p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π^{'} . p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))))) (U)$

Undo the projection

$= (⊤_{Π} ⋉ (λ π^{'} . p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))))) (λ π^{'}, h . U (h))$

Unpack the semidirect product and $⊤_{Π}$ .

$= {inf}_{π^{'}} p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))) (λ h . U (h))$

Remove the projection

$= {inf}_{π^{'}} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π))) (λ π^{''}, h . U (h))$

Unpack the semidirect product and $⊤_{Π}$ again.

$= {inf}_{π^{'}} {inf}_{π} u_{\sim π^{'}}^{1} (Θ (π)) (λ h . U (h))$

Let's fold the two infs into one inf, this doesn't change anything, just makes things a bit more concise.

$= {inf}_{π^{'}, π} u_{\sim π^{'}}^{1} (Θ (π)) (λ h . U (h))$

and unpack the update.

$= {inf}_{π^{'}, π} Θ (π) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

Now, we can note something interesting here. If $π^{'}$ is selected to be equal to $π$ , that inner function is just $U$ , because $Θ (π)$ is only supported over histories compatible with $π$ . If $π^{'}$ is unequal to $π$ , that inner function is $U$ with 1's for some inputs, possibly. So, our choice of $π^{'}$ is optimal for minimizing when its equal to $π$ , so we can rewrite as

$= {inf}_{π} Θ (π) (λ h . U (h))$

and write this as $⊤_{Π}$

$= ⊤_{Π} (λ π . Θ (π) (λ h . U (h)))$

And pack up as a semidirect product

$= (⊤_{Π} ⋉ Θ) (λ π, h . U (h))$

and then because $D = ⊤_{Π} ⋉ Θ$ , we substitute to get

$= D (λ π, h . U (h))$

and then write as a projection.

$= p r_{(A \times O)^{ω} *} (D) (U)$

Now, this is just $D^{p}$ , yielding

$= D^{p} (U)$

and we're done.

Proposition 2: The two formulations of x-pseudocausality are equivalent for crisp acausal belief functions.

One formulation of x-pseudocausality is that

$\forall π, π^{'} : u_{\sim π^{'}}^{1} (Θ (π)) \subseteq Θ^{x} (π^{'})$ where $Θ^{x} (π^{'}) (U) := Θ (π^{'}) (inf (x, U))$

The second formulation is,

$\forall π, π^{'}, μ \in Θ (π) : μ (h ≁ π^{'}) \geq x \cdot {inf}_{ν \in Θ (π^{'})} d_{T V} (μ, ν)$

This proof will be slightly informal, it can be fully formalized without too many conceptual difficulties. We need to establish some basic probability theory results to work on this. The proof outline is we establish/recap four probability-theory/inframeasure-theory results, and then show the two implication directions of the iff statement.

P2.1 Our first claim is that, given any two probability distributions $μ$ and $ν$ , you can shatter them into measures $m^{*}, m_{μ}$ , and $m_{ν}$ such that $m^{*} + m_{μ} = μ$ and $m^{*} + m_{ν} = ν$ , and $m_{μ} (1) = m_{ν} (1) = d_{T V} (μ, ν)$ . What this decomposition is basically doing is finding the largest chunk of measure that $μ$ and $ν$ agree on (that's $m^{*}$ ), and then subtracting that out from $μ$ and $ν$ yields you your $m_{μ}$ and $m_{ν}$ . These measures have no overlap, because if there was overlap, you could put that overlap into the $m^{*}$ chunk of measure. And, the mass of the "unique to $μ$ " piece must equal the mass of the "unique to $ν$ " piece because they must add up to probability distributions, and this quantity is exactly the total variation distance of $μ, ν$ .

P2.2 Our second claim is that

$x \cdot d_{T V} (μ, ν) = {sup}_{U : (A \times O)^{ω} \to [0, x]} | μ (U) - ν (U) |$

Why is this? Well, there's an alternate formulation of total variation distance where

$d_{T V} (μ, ν) = {sup}_{U : (A \times O)^{ω} \to [0, 1]} | μ (U) - ν (U) |$

As intuition for this, we can pick a function U which is 1 on the support of $m_{μ}$ , and 0 elsewhere. In such a case, we'd get

$| μ (U) - ν (U) | = | m^{*} (U) + m_{μ} (U) - m^{*} (U) - m_{ν} (U) | = | m_{μ} (U) - m_{ν} (U) |$

and then remember that $m_{μ}$ and $m_{ν}$ have disjoint supports, so we get

$= | m_{μ} (1) - m_{ν} (0) | = m_{μ} (1) = d_{T V} (μ, ν)$

And any other function in the $[0, 1]$ range wouldn't do as well at attaining different expectation values on $m_{μ}$ and $m_{ν}$ . So that's where the identity comes from. If we try to do the optimal separation but instead restrict $U$ to be in $[0, x]$ , we'd get

$= | m_{μ} (x) - m_{ν} (0) | = m_{μ} (x) = x \cdot m_{μ} (1) = x \cdot d_{T V} (μ, ν)$

and any other utility function in $[0, x]$ wouldn't do as well at separating the two.

P2.3 Our third claim is that the function which maps $f$ to $- \infty$ , if $f$ goes outside of $[0, x]$ , and otherwise maps $f$ to $ψ (f)$ , corresponds to taking the set of sa-measures that is $Ψ$ (the set form of $ψ$ ), and taking the upper completion of it under all signed-measure, b pairs where $b + x \cdot m^{-} (1) \geq 0$ . Call this an x-sa measure. Ie, if $x = \frac{1}{3}$ , then one unit of +b is big enough to cancel out 3 units of negative-measure in the signed measure. Clearly, if $f : X \to [0, x]$ , and $(m, b)$ has $b + x \cdot m^{-} (1) \geq 0$ (is an x-sa measure) then we have

$m (f) + b = m^{+} (f) + m^{-} (f) + b \geq m^{+} (0) + m^{-} (x) + b = x \cdot m^{-} (1) + b \geq 0$

So, adding in the cone of all x-sa pairs like that doesn't actually affect the expectation values of any function bounded in $[0, x]$ at all. However, for any function which goes over the x upper-bound, you can consider a x-sa measure which concentrates all its large amount of negative measure on a point where the function exceeds the upper bound, and exactly compensates for it with the +b term. Adding this on can make the function, evaluated at said point, have an unboundedly negative expectation value, justifying our choice of $- \infty$ for the expectation value.

P2.4 Time for the fourth claim. To build up to it, the monotone hull of a functional $C (X, [0, x]) \to [0, 1]$ is as follows: if $ψ^{x}$ is the original functional, then $ψ^{m}$ is the monotone hull defined by

$ψ^{m} (f) := {sup}_{f^{'} : X \to [0, x] : f^{'} \leq f} ψ^{x} (f)$

Our fourth claim is that, in the set-based value, this operation corresponds to restricting the set of x-sa measures that is $Ψ^{x}$ to just the a-measures in it. Why? Well, we have

$\forall f \in C_{B} (X) : ψ^{m} (f) \geq ψ^{x} (f)$

This is because $ψ^{x}$ and $ψ^{m}$ both agree that any function with negative parts gets $- \infty$ value, and both agree on the expectation of any function bounded in $[0, x]$ , but for functions above 0 which also stray above $x$ somewhere, $ψ^{x} (f) = - \infty$ , while $ψ^{m} (f) \geq 0$ .

Therefore, since $ψ^{m} \geq ψ^{x}$ (when considered as a function, we aren't using the infradistribution reversed ordering here), we have that $Ψ^{m} \subseteq Ψ^{x}$ (higher functions correspond to smaller sets). Now, $Ψ^{m}$ cannot contain any x-sa-measures with negative measure anywhere in the measure component. For, if there was such a point in there, we could consider a function $f$ that assigned extremely high value to the region of negative measure, and 0 value elsewhere, and $f$ would attain a negative expectation value on that x-sa measure, which contradicts the nonnegative worst-case expectation value of $f$ due to how $ψ^{m}$ was defined. So, the set $Ψ^{m}$ must consist entirely of a-measures. Further, for any function $f$ with range in $[0, x]$ , it is minimized by an a-measure in $Ψ^{x}$ , and the same point is present in $Ψ^{x} \cap M^{a}$ (no extra a-measures added), so the $ϕ$ corresponding to that set must assign the exact same expectation value to $f$ as $ψ^{x}$ and $ψ^{m}$ do. Also, any set consisting entirely of a-measures must have its expectation functional be monotone.

So, recapping what we've done so far, we know that $Ψ^{m} \subseteq Ψ^{x}$ . We know that $Ψ^{m}$ must consist entirely of a-measures, otherwise we'd get a contradiction with monotonicity. Further, $Ψ^{x} \cap M^{a}$ (the biggest set that $Ψ^{m}$ could possibly be) has its expectation functional $ϕ$ agree with $ψ^{x}$ on the expectations of functions in $[0, x]$ , and it's monotone like $ψ^{m}$ is. Now, if $Ψ^{m} \subset Ψ^{x} \cap M^{a}$ (strict subset), we'd have the functional $ϕ$ corresponding to the intersection being strictly below $ψ^{m}$ on some function. However $ψ^{m}$ is the minimal monotone function that agrees with $ψ^{x}$ on the expectations of functions in $[0, x]$ , so this rule out strict subset, and we must have equality. The monotone hull of an expectation functional corresponds to the restriction to the set to a-measures. Further, we can rewrite the definition

$ψ^{m} (f) := {sup}_{f^{'} : (A \times O)^{ω} \to [0, x] : f^{'} \leq f} ψ^{x} (f)$

as just

$ψ^{m} (f) := ψ^{x} (inf (x, f))$

And we're done with this.

Putting claims 3 and 4 together, we can now express what the set $Θ^{x} (π^{'})$ is, from our definition of $Θ^{x} (π^{'}) (U) := Θ (π^{'}) (inf (x, U))$ . $Θ^{x} (π^{'})$ (interpreted as a set of sa-measures) is just the upper completion of $Θ (π^{'})$ under x-sa measures, those with $b + x \cdot m^{-} (1) \geq 0$ (this is the restriction to $[0, x]$ ), and then the intersection of that set with the cone of a-measures (monotone hull), and then upper completion under sa-measures (the restriction to $[0, 1]$ ).

P2.5 Time to begin showing one direction of the iff statement. Remember, we're assuming that all the $Θ (π)$ are induced by a set of probability distributions, they're crisp. We'll start with the easy direction, that

$\forall π, π^{'}, μ \in Θ (π) : μ (h ≁ π^{'}) \geq x \cdot {inf}_{ν \in Θ (π^{'})} d_{T V} (μ, ν)$

implies

$\forall π, π^{'}, U : u_{\sim π^{'}}^{1} (Θ (π)) (U) \geq Θ^{x} (π^{'}) (U)$

where $Θ^{x} (π^{'}) (U) := Θ (π^{'}) (inf (x, U))$ . (well, technically, this shouldn't just be continuous functions, but lower-semicontinuous functions as well) To begin with, let $π, π^{'}, U$ be arbitrary with $U$ bounded in $[0, 1]$ . We can start unpacking

$u_{\sim π^{'}}^{1} (Θ (π) (U)) = Θ (π) (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

Now, this minimal value must be attained by some minimal point in $Θ (π)$ , which is some probability distribution $μ$ . So, we have

$= μ (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

We can, at this point, select the closest probability distribution to $μ$ in $Θ (π^{'})$ according to total variation distance, call that $ν$ . We do our usual shattering of $μ$ into $m^{*}$ and $m_{μ}$ , the chunk of measure where $μ$ and $ν$ overlap, and the chunk of measure that's unique to $μ$ . Note that the chunk of measure where $μ$ and $ν$ overlap must be supported on histories compatible with $π^{'}$ since $ν \in Θ (π^{'})$ , so we can break things down as

$= m^{*} (U) + m_{μ} (λ h . 1_{h \sim π^{'}} U (h) + 1_{h ≁ π^{'}})$

And then we can break $m_{μ}$ down further into $m_{μ, \sim π^{'}}$ and $m_{μ, ≁ π^{'}}$ , for the chunk of measure on histories compatible with $π^{'}$ and incompatible, respectively, yielding

$= m^{*} (U) + m_{μ, \sim π^{'}} (U) + m_{μ, ≁ π^{'}} (1)$

Which can be rephrased as

$= m^{*} (U) + m_{μ, \sim π^{'}} (U) + μ (h ≁ π^{'})$

Now it's time for some inequalities, explained afterwards.

$m^{*} (U) + m_{μ, \sim π^{'}} (U) + μ (h ≁ π^{'}) \geq m^{*} (U) + μ (h ≁ π^{'}) \geq m^{*} (inf (U, x)) + μ (h ≁ π^{'})$

$\geq m^{*} (inf (U, x)) + x \cdot d_{T V} (μ, ν) = m^{*} (inf (U, x)) + {sup}_{U^{'} : (A \times O)^{ω} \to [0, x]} | ν (U^{'}) - μ (U^{'}) |$

$= m^{*} (inf (U, x)) + {sup}_{U^{'} : (A \times O)^{ω} \to [0, x]} | m^{*} (U^{'}) + m_{ν} (U^{'}) - m^{*} (U^{'}) - m_{μ} (U^{'}) |$

$= m^{*} (inf (U, x)) + {sup}_{U^{'} : (A \times O)^{ω} \to [0, x]} | m_{ν} (U^{'}) - m_{μ} (U^{'}) |$

$= m^{*} (inf (U, x)) + m_{ν} (x) \geq m^{*} (inf (U, x)) + m_{ν} (inf (U, x)) = ν (inf (U, x))$

$\geq {inf}_{ν^{'} \in Θ (π^{'})} ν^{'} (inf (U, x)) = Θ (π^{'}) (inf (U, x)) = Θ^{x} (U)$

So, for the first line, the first two inequalities are obvious. For the second line, the initial inequality is us invoking the total variation distance variant of x-pseudocausality since $ν$ is as close as possible to $μ$ while also being in $Θ (π^{'})$ , and the equality is reexpressing total variation distance in accordance with our second claim. The third line is just shattering $ν$ and $μ$ in our way connected with total variation distance, and the fourth line is just canceling. For the fifth line, the first equality is the supremum being attained by a function that's $x$ on $m_{ν}$ , and 0 on $m_{μ}$ , as the two measures are disjoint, and the second equality is $ν = m^{*} + m_{ν}$ . Then, for line 6, the inequality is obvious because $ν \in Θ (π^{'})$ , and then we just wrap the inf up as an expectation according to $Θ (π^{'})$ , and apply the definition of $Θ^{x} (π^{'})$ .

P2.6 Now for the other direction of the iff-statement, going from

$\forall π, π^{'}, U : u_{\sim π^{'}}^{1} (Θ (π)) (U) \geq Θ^{x} (π^{'}) (U)$

to

$\forall π, π^{'}, μ \in Θ (π) : μ (h ≁ π^{'}) \geq x \cdot {inf}_{ν \in Θ (π^{'})} d_{T V} (μ, ν)$

Using our set-based characterization of inframeasure ordering, we can accurately rephrase our initial statement as

$\forall π, π^{'} : u_{\sim π^{'}}^{1} (Θ (π)) \subseteq Θ^{x} (π^{'})$

The former set is "take all the minimal points of $Θ (π)$ , convert all their measure on histories incompatible with $π^{'}$ to the +b term, do closed convex hull and upper completion", and the latter set is "take $Θ (π^{'})$ , do upper completion w.r.t. the cone of x-sa measures, restrict to just the a-measures, and then add in the cone of sa-measures again"

Pick a $μ \in Θ (π)$ . When we 1-update it on compatibility with $π^{'}$ , we get $(m_{μ, \sim π^{'}}, μ (h ≁ π^{'}))$ . And said point lies in $Θ^{x} (π^{'})$ , which means it must be possible to create by taking a minimal point in $Θ (π^{'})$ (call that one $ν$ ), and adding an x-sa measure to it. Call the x-sa measure $(m^{'}, b^{'})$ . So, our net result is:

$(m_{μ, \sim π^{'}}, μ (h ≁ π^{'})) = (ν, 0) + (m^{'}, b^{'})$

The update of $μ$ equals $ν$ plus an x-sa measure. Now, breaking up $m^{'}$ into its positive and negative parts which are disjoint, $(m^{'})^{+}$ and $(m^{'})^{-}$ , we can rewrite things as:

$b^{'} = μ (h ≁ π^{'})$

$m_{μ, \sim π^{'}} = ν + (m^{'})^{+} + (m^{'})^{-}$

Adding $m_{μ, ≁ π^{'}}$ to both sides and folding it into $μ$ , and rearranging a bit and adding parentheses, that second equality can be restated as

$μ = ν + ((m^{'})^{+} + m_{μ, ≁ π^{'}}) + (m^{'})^{-}$

Now, $ν$ is supported entirely over histories compatible with $π^{'}$ , and $(m^{'})^{-}$ is a chunk of negative measure taken out of $ν$ , so $(m^{'})^{-}$ must be supported entirely over histories compatible with $π^{'}$ . Also, $(m^{'})^{+}$ and $(m^{'})^{-}$ are disjoint (Jordan decomposition), and $m_{μ, ≁ π^{'}}$ is supported entirely over histories incompatible with $π^{'}$ , so the positive measure $(m^{'})^{+} + m_{μ, ≁ π^{'}}$ and the negative measure $(m^{'})^{-}$ must be disjoint. Since $μ$ is made from $ν$ by adding on a chunk of positive measure and a chunk of negative measure which are disjoint, we have $d_{T V} (μ, ν) = - (m^{'})^{-} (1)$ . At this point, we only have one step left.

For the last step, because $((m^{'})^{+} + (m^{'})^{-}, b^{'})$ is an x-sa measure, we have $b^{'} + x \cdot (m^{'})^{-} (1) \geq 0$ . Also, because $b^{'} = μ (h ≁ π^{'})$ , our inequality turns into

$μ (h ≁ π^{'}) + x \cdot (m^{'})^{-} (1) \geq 0$

$μ (h ≁ π^{'}) \geq - x \cdot (m^{'})^{-} (1)$

$μ (h ≁ π^{'}) \geq x \cdot d_{T V} (μ, ν)$

and this gets us our

$\forall π, π^{'}, μ \in Θ (π) : μ (h ≁ π^{'}) \geq x \cdot {inf}_{ν \in Θ (π^{'})} d_{T V} (μ, ν)$

result. We're done!

Proposition 3: If a utility function $U$ is bounded within $[0, x]$ and a belief function $Θ$ is x-pseudocausal, then translating $Θ$ to $Θ^{p}$ (pseudocausal translation) fulfills $\forall π : Θ^{p} (π) (U) = Θ (π) (U)$ .

Blessedly, this one is very easy. First, let's recap the translation of a belief function (assumed to be x-pseudocausal) from acausal to pseudocausal. It is

$Θ^{p} (π^{'}) := p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π))))$

So, applying this, we have

$Θ^{p} (π^{'}) (U) = p r_{(A \times O)^{ω} *} (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))) (U)$

$= (⊤_{Π} ⋉ (λ π . u_{\sim π^{'}}^{1} (Θ (π)))) (λ π, h . U (h)) = {inf}_{π} u_{\sim π^{'}}^{1} (Θ (π)) (U)$

And then we recall that x-pseudocausality is $\forall π, π^{'}, U : u_{\sim π^{'}}^{1} (Θ (π)) (U) \geq Θ^{x} (π^{'}) (U)$ Also, recall that since $Θ^{x} (π^{'}) (U) := Θ (π^{'}) (inf (U, x))$ , and our utility function is bounded in $[0, x]$ , we get the statement $\forall π, π^{'} : u_{\sim π^{'}}^{1} (Θ (π)) (U) \geq Θ (π^{'}) (U)$ Additionally, $u_{π^{'}}^{1} (Θ (π^{'})) = Θ (π^{'})$ . Therefore, the infinimum is attained by $π^{'}$ itself, and we get

$= Θ (π^{'}) (U)$

and we're done!