Tl;dr, A choice of variable in causal modeling is good if its causal effect is consistent across all the different ways of implementing it in terms of the low-level model. This notion can be made precise into a relation among causal models, giving us conditions as to when we can ground the causal meaning of high-level variables in terms of their low-level representations. A distillation of (Rubenstein, 2017).
Motivation
1) Causal Inference
Say you're doing causal inference in the Pearlian paradigm. Usually, your choice of variables is over high-level concepts of the world rather than at the level of raw physics.
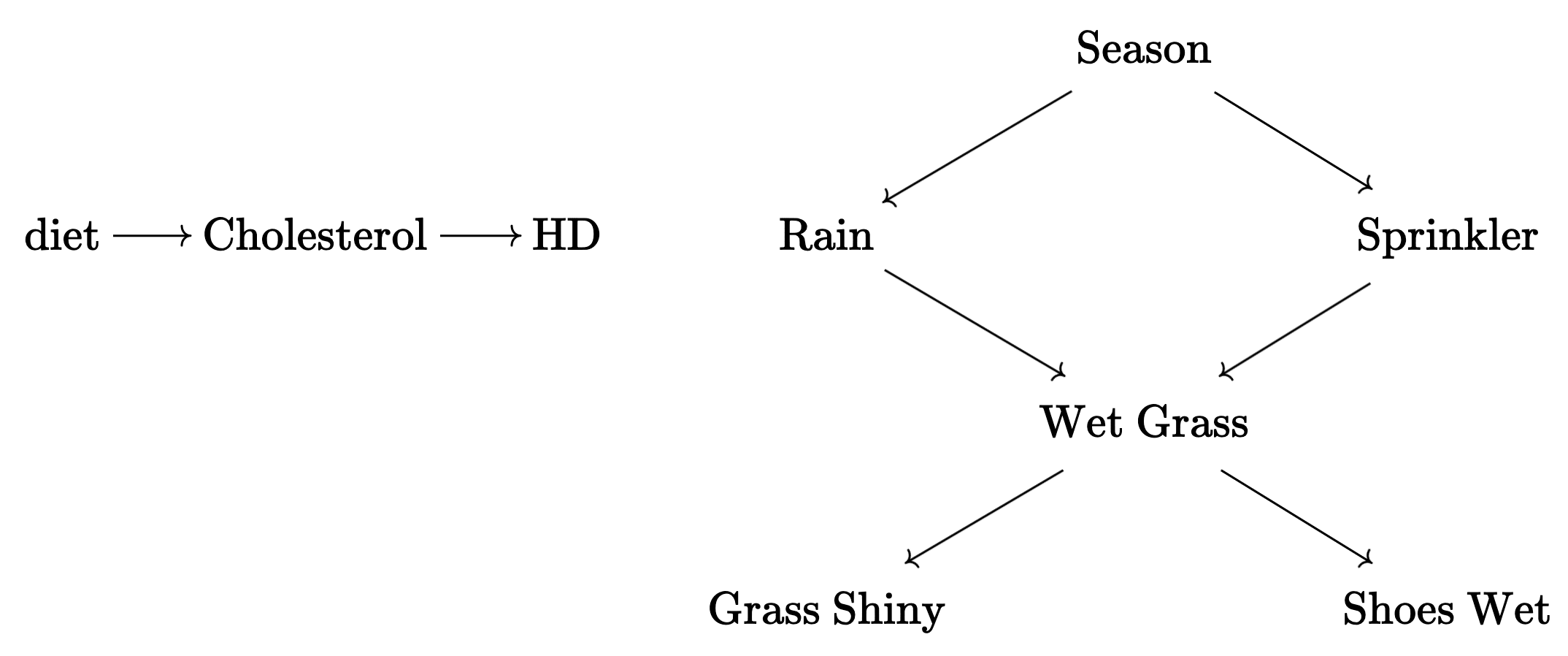
Given my variables, I can (well, in principle) perform experiments and figure out the causal structure over them. I intervene on my neighbor's sprinkler while holding everything still and notice that it results in a variation of the wetness of the grass! I perform cloud seeding to make it rain and voila, my grass is wet!
But soon I notice a problem. Say I want to find out if cholesterol levels—measured by adding up the level of low-density lipoprotein (LDL) and high-density lipoprotein (HDL) in the body—cause heart disease. So I survey the literature and find various papers that do so by intervening on the diet (which is known to causal cholesterol levels to change).
Then I find inconsistent results: some paper says high cholesterol increases HD, others give the opposite result. What is going on?[1]
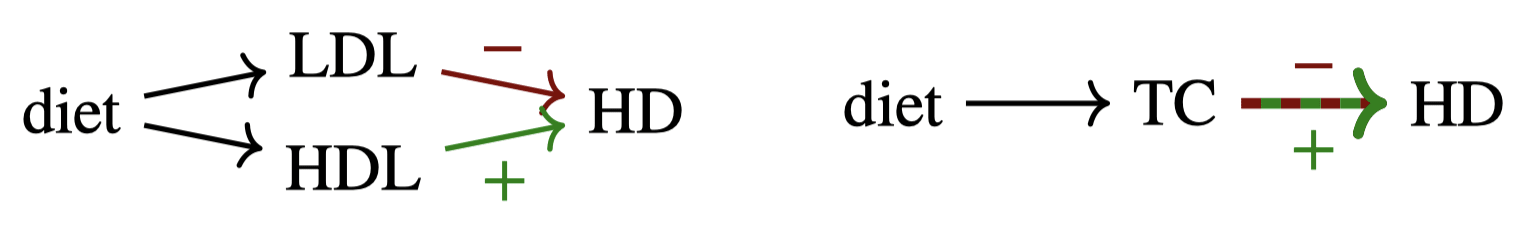
Turns out, if we use LDL and HDL as variables rather than Cholesterol, we get a consistent result, because LDL and HDL respectively has negative and positive effects on HD. The problem was in the choice of variables, i.e. how we factorize the world.
More concretely:
- Cholesterol is a high-level variable that combines LDL and HDL.
- Implementing an intervention over a high-level variable must translate into interventions over low-level variables that we can actually control, which is LDL and HDL in this case.
- The intervention "set Cholesterol as C" can thus be implemented in many different ways of the form "set LDL as , HDL as ."
- The reason why it's bad to consider Cholesterol as the primitive variable of your causal model is because different (low-level) implementations of the same (high-level) intervention over Cholesterol levels result in different outcomes.
So it seems like, in the context of analyzing the causal effects on Heart Disease, "intervening on Cholesterol" wasn't a consistent thing to do, relative to the lower-level causal model.
Some things to note:
- Cholesterol might become a good variable if the context was different. Perhaps some diseases only causally depend on the total cholesterol level while being invariant to the specific LDL and HDL level composing it.
- As with Cholesterol, there are many ways to implement interventions over LDL/HDL in terms of interventions over causal models at even lower levels, e.g., specific atomic configurations. The point is that these differences can be abstracted away, because all these different ways of implementing the same LDL/HDL values lead to same effects on HD (at least in this example).
2) Use of Pearlian Causality in Alignment
(This is how I originally arrived at this question. You can skip this section.)
One of my main issues with most applications of Pearlian causality is that it assumes we're given variables that correspond to high-level things in this world, which is hiding a lot of work. Here's an example:
My research interest is in developing algorithms that can detect agents / boundaries embedded in a system. In that direction, Discovering Agents provide an algorithm that claims to do so using causal interventions based on a reasonable operationalization of the intentional stance.
I found the work to be quite clarifying, so I've been musing over the several immediate conceptual and practical issues that arise when thinking of what it would take to actually implement their algorithms in practice.
One pretty fundamental confusion I had was the following: "What does it mean, in practice, to perform an intervention over variables representing abstractions over reality? When does such a notion even make sense?" Let me explain.
The DA algorithm assumes the ability to perform arbitrary interventional queries (i.e. experiments) on the system that we want to detect agents within. With this ability, it first reconstructs the causal model of the system in question. Below is an example of a causal diagram for an actor-critic system, whose arrows are found using this process. (Ignore the suggestive node labels and arrow colors.)
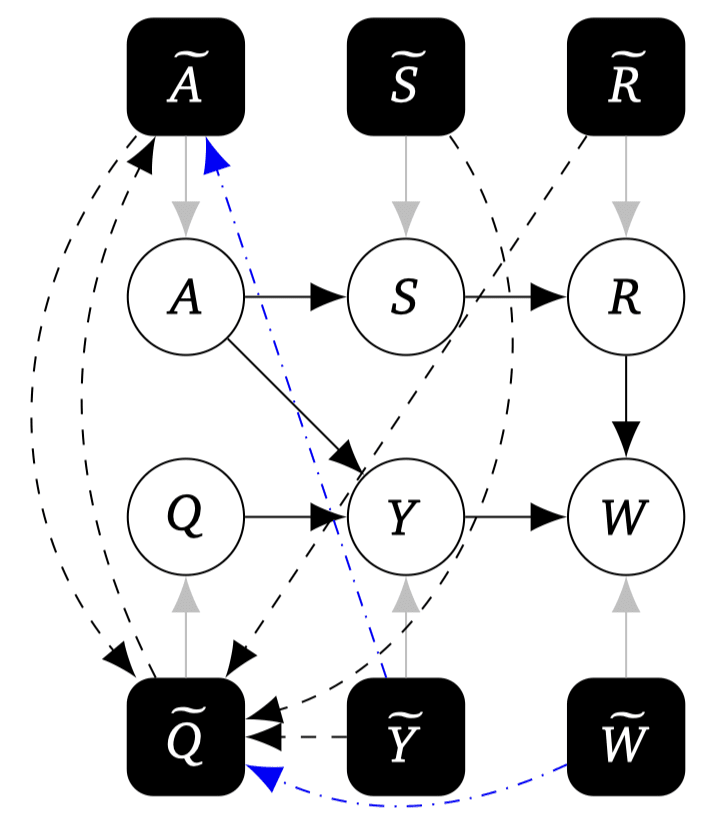
Given this causal model, the DA algorithm performs appropriate causal interventions across the variables to find variables ones that behave like an agent in the intentional stance sense. The criteria looks something like:
- "for a node to represent an agent's utility, its associated (supposed) decision node must respond to changes in the utility node even when the utility's causal influence on its children is cut off—otherwise, that'd imply that the decision node only cared about the utility node for instrumental reasons."
Then, the algorithm will appropriately label the nodes into Decision (diamond), Utility (square), Chance (circle) nodes, with labels (colors) as to which belongs to which agent. In the case of the above setup, it correctly discovers that there are two agents.
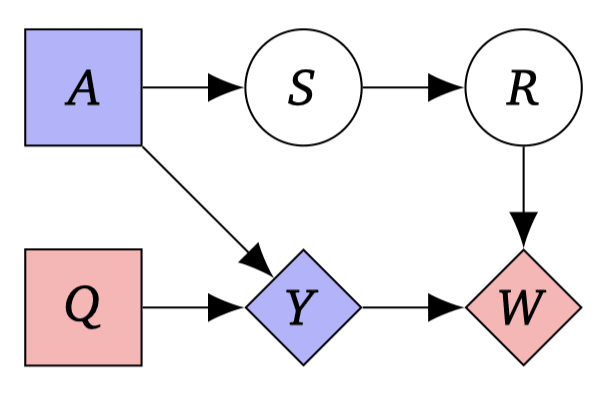
This is pretty cool!
Except, one massive assumption here is that the variables the DA algorithm has interventional access to (e.g., variables) are very convenient abstractions over the underlying low-level causal structure, in a way that admits the variables to be naturally classified into either [Decision / Utility / Chance].
This is hiding a lot of work. In reality, all we have access to is the low-level causal structure. We don't want to assume a factorization, we want to discover one! Think of a computational graph corresponding to the entire training history of the above actor-critic system. It would have number of nodes.
Let's ignore the practical question of how to discover such high-level causal models in a tractable way. The question I want to ask here is more fundamental: what does it even mean for us to be able to provide the DA algorithm interventional access to the "high-level causal models," when all we have is that of the lower level model?
Concretely, how should causal queries in one representation of the system be translated into causal queries over another representation of the system?
- Say the DA algorithm queries us with the following: "I want to know how the probability of changes when I intervene on in such and such way." How do we translate this in terms of actual interventions to be made in the gigantic raw computational graph? e.g., which weights of the NN to edit, how to edit them, etc."
Desiderata for Causal Consistency
(This section assumes basic knowledge of the definition of a structural causal model, though look at this footnote for a brief overview[2].)
- (Notation: We denote an SCM over endogenous variables as , each corresponding to [set of functional equations / set of allowed interventions / probability over the exogenous variables]. denotes the distribution over induced by .)
The paper Causal Consistency of Structural Equation Models by Rubenstein gives us a fairly satisfying answer to this question.
Specifically, Rubenstein asks the following question. Given:
- Two causal models
- A function that maps variable values of exogenous variables over one model to another
- A function that maps between interventions of one model to another
... when can we say the interventions over the second model are, in the sense discussed earlier, consistent with the first model?
Let's make this notion more precise.
The desiderata can be summarized by saying that the following diagram commutes. Uhh Please don't leave! I will explain them in hopefully easy terms.
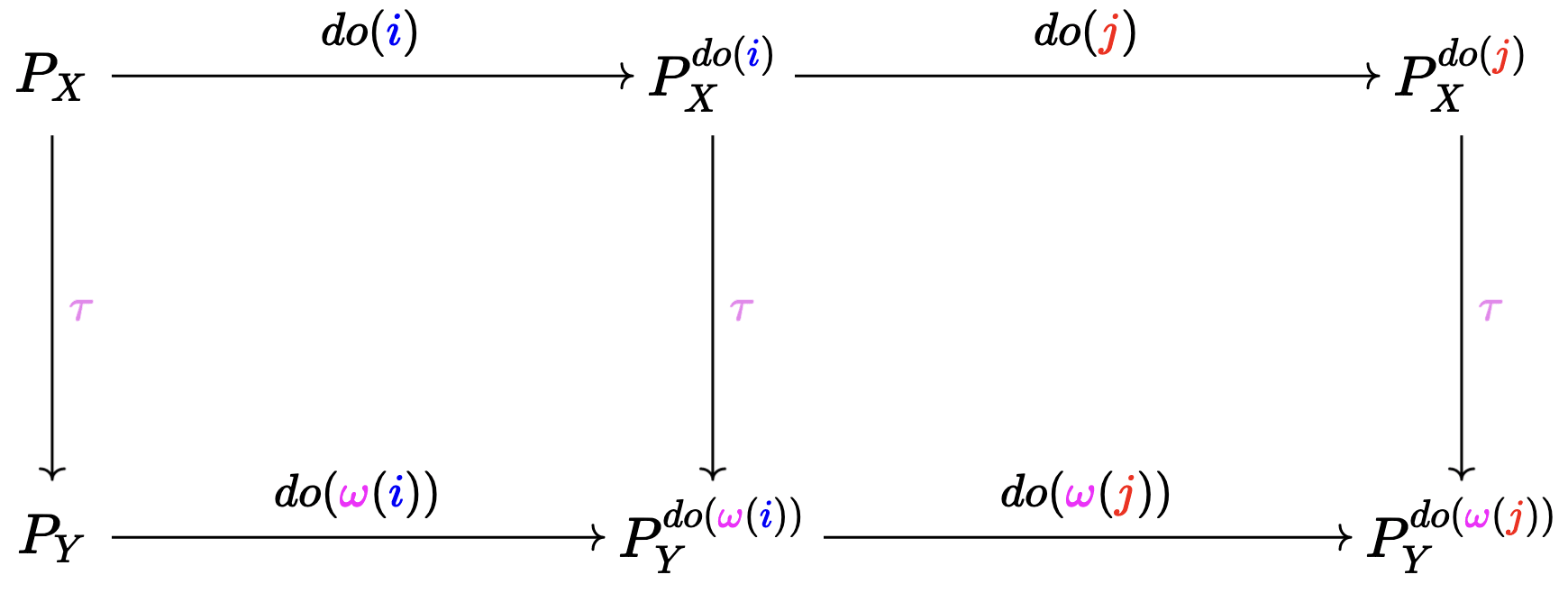
When I say a "diagram commutes", it means that if I travel through the diagram in two different paths (with each edge representing the application of some operation) and arrive at the same point, the values should be the same.
To aid our intuition, let's think of Y as representing an abstracted, high-level version of X, even though we will later see that this interpretation doesn't always make sense.
Let's look at each of the squares one by one.
We want the left square to commute
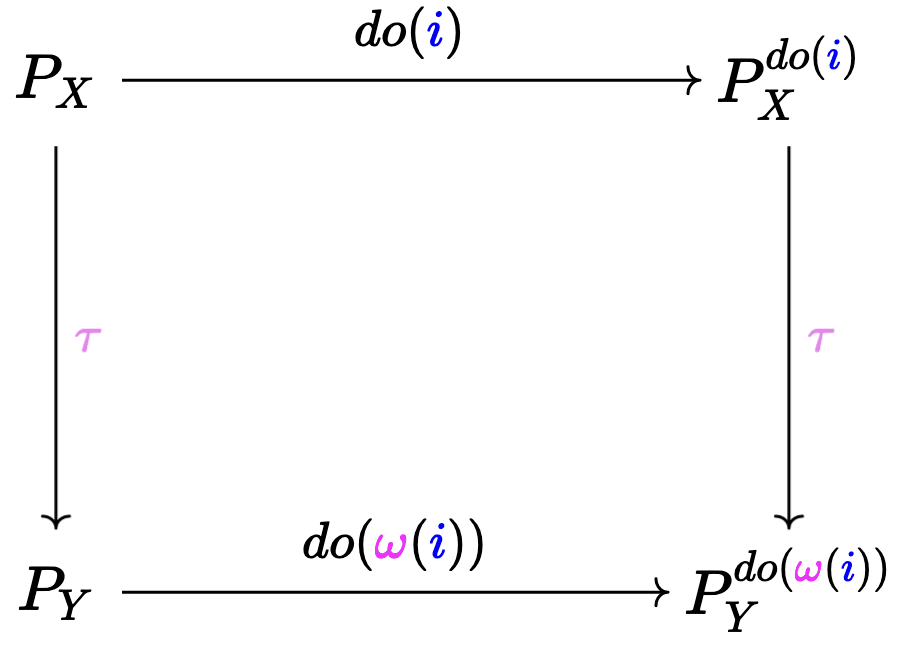
Let represent some low-level intervention, . Now let's see what the two different paths from to intuitively represent, and whether the fact that these two paths give us the same outcome match our intuitive notion.
"Suppose we intervened at the low-level, and mapped[3] it to a high-level . Then, we should get the same result even if we mapped it to the high-level first, and only then intervened, but with the high-level version of , i.e. ."
That makes sense! If we have maps that translate across different model levels, whether
In terms of the cholesterol example, say represents two different interventions that sets the value of LDL/HDL pair, but in a way that the value of is the same.
Then, that means the 'down-right' path for both and would result in a same , because . Meanwhile, since and have different effects (recall, that's why we concluded Cholesterol was a bad variable in the Heart Disease context), so the result reached via the 'right-down' path won't in general match, .
So, doesn't let the diagram commute, but it would commute if it turned out its effects were consistent across varying low-level LDL/HDL implementations.
Promising so far! Let's now move on to the right square.
We want the right square to commute
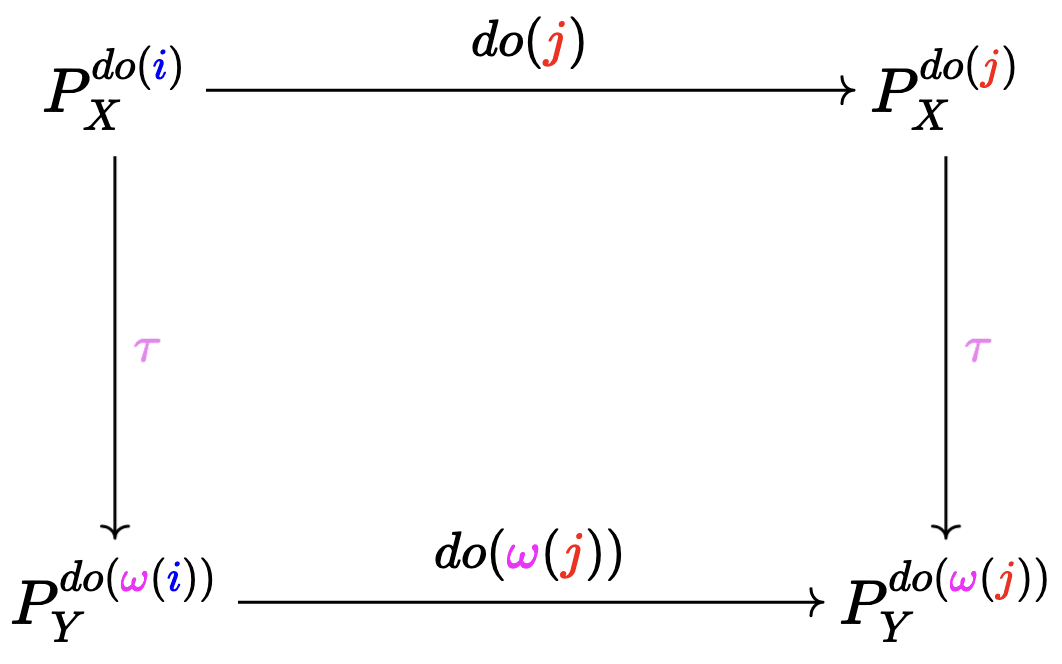
Here, , but with one requirement: . What does this mean? It means that intervenes on a subset of variables that intervenes on, and sets them to the same value as does.
So, to say that the right square commutes intuitively means that the aforementioned "consistency" from the left square should continue to hold as you further intervene on the remaining variables of and .
must be surjective
This is an addition requirement (not present in the diagram). It intuitively means that any interventions on the high-level must be actually be implementable in the low-level, i.e. .
Intuitively, a high-level intervention can only be meaningful if it is actually physically implementable in some way! i.e. "causal variables of are rooted in reality."
In the example above for the Discovering Agents algorithm, it means that we're able to find an actual experiment in terms of low-level variables like NN weights in order to answer the algorithm's causal query over the high-level variables.
Exact Transformation
Rubenstein defines a notion of Exact Transformation between SCMs, and proves that when one SCM is an exact transformation of another, it implies that the earlier diagram commutes[4].
Given and and a map between the endogenous variables , we say is an exact -transformation of if there exists a surjective order-preserving map such that .
Things to note:
- The complicated equation there basically says "the left square commutes."
- An order-preserving map means , with the natural order over allowed interventions as defined earlier. This is what lets "the right square commute."
Example: Dynamical Process
Then, the paper proceeds with various examples of exact transformations. An example that I found especially interesting was the case of a discrete-time linear dynamical process.
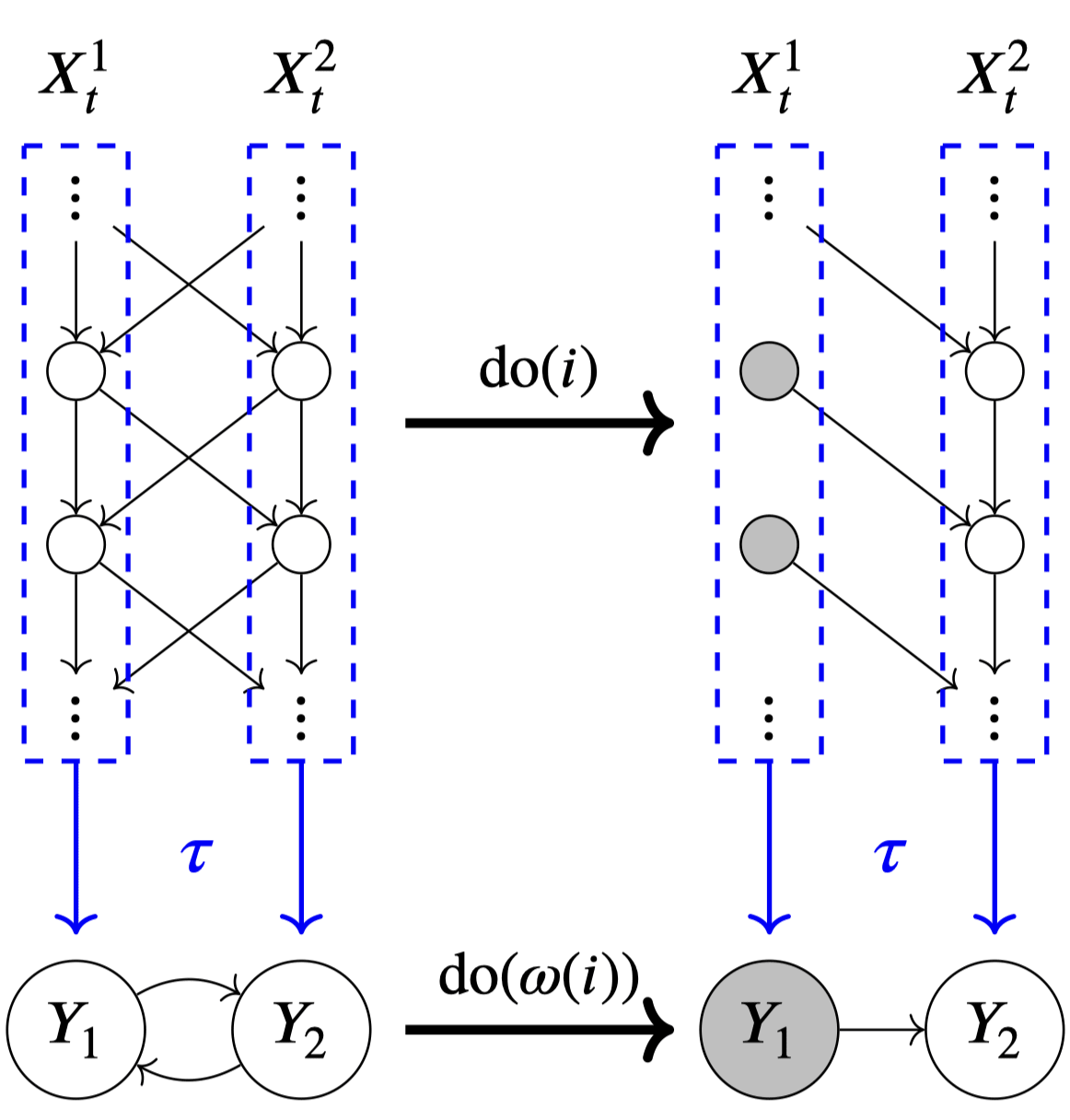
If we let the SCM consist of variables , ( for figure above), its exact transformation is a SCM over the variables where is , a map that converts the history of the dynamical system to its stationary values.
Interestingly, even though the original SCM was acyclic (arrows always point from the past to the future), the exact transformation's SCM may have cyclic structure.
This is one way in which causal models that contain cyclic structures may arise, even though our physical universe is acyclic.
Answering our Original Question
To answer our original questions using this new vocabulary: the meaning of causal queries over a variable in a model can be grounded in terms of causal queries in a model ' that is an exact transformation of (relative to a map ).
There's an subtle point here: this kind of feels like turtles all the way down: "When are my variables good? Well, if they can be grounded on a causal model that I trust. Well, how do you know if that causal model is any good? etc etc."
In practice, there seems to be a reasonable level at which the entire thing grounds out:
- inductively say that a model is good if it is an exact transformation of another model that we already trust have consistent interventional outcomes (for some query we care about) wrt another model
- base case: physics, computation, etc.
In the Cholesterol example, we noted that the model involving LDL/HDL is a good choice, because experimentally it seemed to yield consistent interventional results for varying ways of actually implementing the same .
- So the LDL/HDL model can be considered an exact transformation of some "~macroscopic physics-y model."
In the Discovering Agents example, this then becomes an algorithm specification:
- The high-level SCM that the Discovering Agents algorithm operates on must be an exact transformation of the "underlying raw computational graph."
Notes on Abstraction
Earlier, we interpreted an exact -transformation of as representing an abstracted, high-level version of . This interpretation isn't really correct. We should instead interpret exact transformations more like relations between causal models that describe when interventional queries of can be grounded-to/made-consistent-with interventional queries of .
Why not? Abstracting Causal Models by Beckers and Halpern give several examples in which while M_Y is an exact transformation of M_X, it isn't necessarily "simpler" in any intuitive sense. They instead propose three additional definitions that gradually add more and more constraints to the exact transformation definition, and claim those to better capture what we intuitively mean by "abstraction."
If you read this post so far, the Beckers and Halpern paper should be fairly readable. Also check out this post for a summary of it.
- ^
At least, that's the example given in Rubenstein, 2017) I have not checked their validity, since it doesn't really matter in the context of this post.
- ^
Structural Causal Model (SCM) is a type of causal model over variables .
- We assume that the variables are related to one another through deterministic functional relationships, .
- But doing so can't model anything probabilistic! So SCM introduces randomness by associating each with a "noise variable" variable , and making the deterministic functional relationships take the form .
- We assume that the values of E determine the values of X. This is the case when, for example, the functions depend on each other acyclically. So we denote them by .[5]
- is associated with a probability distribution . Then, this induces a distribution over . That's how uncertainty is introduced.
Given this basic structure, we define interventions as follows:
- Intervention is defined as an operation that transforms an SCM into a different SCM. Specifically, "intervene on and set its value to " is defined by copying the SCM and replacing the functional equation with .
- To indicate an intervention that sets a variable (or a set of variables) to a particular value, we write . Examples:
- is the conditional distribution of given . This can be calculated by first computing the distribution induced by and calculating the conditional from it.
- is calculated by 1) performing the aforementioned SCM surgery, and calculating from that new model.
With this, we denote an SCM over as , each corresponding to [set of functional equations / set of allowed interventions / probability over the exogenous (i.e. noise) variables].
- ^
Note that applying to a distribution represents , i.e. total probability of all -s that get mapped to under . Intuitively, it "push-forwards" a distribution over to a distribution over using a map.
- ^
Honestly, this definition is just another way of saying "the earlier diagram holds," so if it doesn't make sense you can skip it as long as the commutative diagram section made sense.
- ^
Rubenstein actually doesn't require acyclicity, just that under any intervention (including no intervention), there is a unique solution to the structural equations (with probability wrt ).