G Gordon Worley III recently complained about a lack of precision in discussions about whether Goodhart's Law will present a fatal problem for alignment in practice. After attending a talk in which Dylan Hadfield-Menell[1] presented the "Goodhart's Law will be a big deal" perspective, I came away with a relatively concrete formulation of where I disagree. In this post I'll try to explain my model for this, expanding on my short comment here.
More specifically, in this post I'll discuss proxy misspecification, which I view as a subproblem of Goodhart's Law (but not necessarily the entirety of it).
Our model of proxy misspecification
First I'll borrow Hadfield-Menell's mathematical model of the proxy misspecification problem. Suppose:
- Alice has things which she values, i.e. she has a utility function which is increasing in each .
- A robot is given a proxy utility function which depends on some strict subset of the 's.
- The robot optimizes by freely varying all , subject only to resource constraints that require the to trade off against each other.
Then, as you'd expect, it's a theorem that the robot will set to their minimum possible values all on which the proxy utility function does not depend (instead putting all resources to increasing the 's which does take into account).
To borrow an example from the paper, we can imagine that the robot is a content recommendation algorithm. Then the 's might be metrics for things like ad revenue generated, engagement quality, content diversity, and overall community well-being. Humans care about all of these things, but our content recommendation algorithm might have a proxy reward that depends only on the first two. Furthermore, the algorithm only gets to recommend a limited amount of content, a resource constraint which (let's assume) prevents it from making all of these metrics as good as possible. In that case, according to the model, the algorithm will recommend content in a way that minimizes the features on which its proxy reward doesn't depend: content diversity and overall community well-being.
My complaint: it might be hard to decouple the 's
The above formulation of the proxy misspecification problem is a theorem. So if I'm going to resist the conclusion that future AI systems will destroy all value that their proxy rewards don't take into account, then I'll need to dispute part of the set-up or assumptions. Indeed, I'll attack the assumption that the robot is able to freely vary the 's subject only to resource constraints.
In reality, many of the things we care about are highly correlated over "easily attainable" world states. Or in other words, for many pairs of things we care about, it's hard to increase without also increasing . Furthermore, given a triple of things we care about, it's even harder to increase and without also increasing . And so on for quadruples, quintuples, etc. with it getting harder to decouple one thing we value from an -tuple of other things we value as grows larger.[2]
What work is being done by the word "hard" in the previous paragraph? One interpretation: finding ways to decouple the things human value and vary them freely requires sufficiently strong AI capabilities. And as the proxy utility function takes into account more of the and becomes a better approximation of , the capabilities level needed to decouple the 's on which depends from the rest increases.
And if you buy all of this, then a corollary is: for each fixed capabilities level, there is an acceptable "margin of error" for our proxy utility functions such that if is within this margin of error from , then an AI system with said capabilities level and proxy utility will approximately optimize for . As capabilities improve, this safe margin of error shrinks.
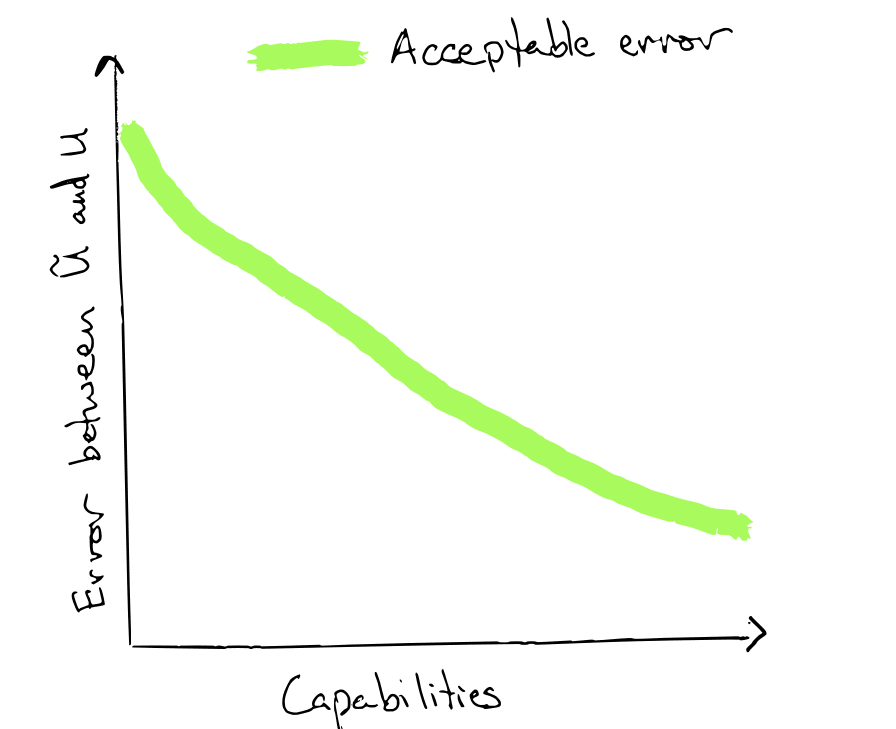
The capabilities vs. value learning race
As time goes on, AI capabilities will improve, so the acceptable margin of error[3] between the proxy utility function and our true utility function will shrink. This might seem to suggest doom (since eventually AI systems will become capable enough to maximize their proxy utility functions while destroying everything else we value).
But there is cause for hope: as general capabilities improve so might value learning capabilities. In other words, if you think that future AI systems will learn their proxy reward from humans (via human feedback, IRL, CIRL, etc.), then you can model the future as a race between increasingly accurate proxy utility functions and increasingly narrow acceptable margins for inaccuracy.
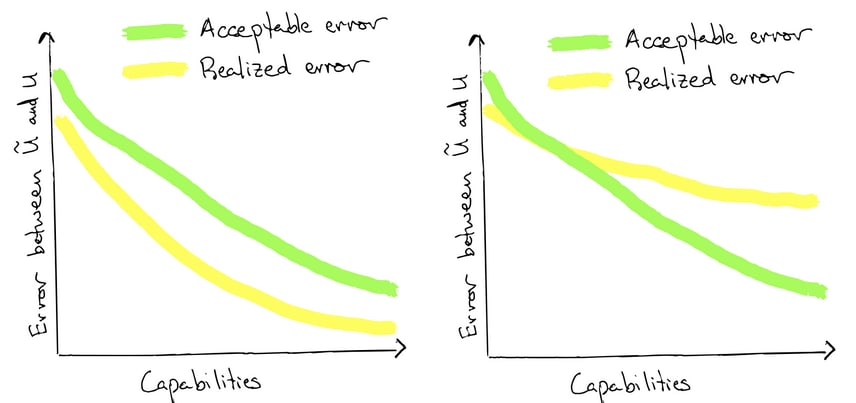
The above graphs show the two ways the race could go. On the left: value learning improves fast enough to keep proxy rewards within the margin of error; we are safe. On the right: value learning is unable to keep up; AI systems destroy much of what we value.
Improving value learning corresponds to pushing down the yellow line. Other types of safety work, like impact regularization or work on safe exploration, might help move the green line up.[4]
It doesn't seem obvious to me how this race will go by default; in fact, the likely trajectories seem to depend on lots of empirical facts about the world that I don't have strong views on. Relevant considerations include:
- How Goodhart-able are human values? Or more precisely, how narrow is the safe margin of error for a given capabilities level?
- One way to get information about this is to argue a lot about air conditioner models. We can treat "the market" as an optimizer with some fixed capabilities level and a proxy utility function that takes into account things like profit generated, consumer ratings, professional reviewer ratings, etc. If optimizing for this proxy reward already produces very different outcomes than optimizing for true consumer preferences, this provides some information about the general trend for the acceptable margin of error.
- What is the likely trajectory of value learning? Will it scale to learn proxy rewards that stay within the margin of error?
- Will our ability to correctly evaluate how happy we are with completed tasks be a bottleneck?
- Will our value learning algorithms have a useful inductive bias?
... as well as probably many others.
These considerations are relatively concrete and amenable to discussion. My hope is that by discussing them (and other considerations like them), the "Goodhart's Law is a fatal obstruction to alignment" people and the "Goodhart's Law won't be a big problem in practice" people won't talk past each other as much.
- ^
This isn't the recording from the talk I attended, but it seems to be identical in content.
- ^
More precisely, we shouldn't model agents as freely choosing states. Rather, we should model them as choosing actions (from a much lower-dimensional space!) which influence states. Each action might influence many of the features that we care about, hence the apparent correlation between 's. Thanks to Ben Edelman for suggesting this model (which is present in these papers that study proxies which work well despite Goodharting).
- ^
I'm going to keep using the word "error" informally to mean a measure of dissimilarity between and , but I don't actually have in mind a particular metric that we could use to quantify how different a proxy utility function is from a given utility function. Sorry if this is confusing.
- ^
Note also that depending on what you think about a whole bunch of other safety-relevant problems (mesa-optimizers, robustness to distributional shift, etc.), you might think that by default the safe margin of error for high capabilities levels is negative, i.e. that we won't be safe even with a proxy utility function that perfectly matches our true utility function. To be clear, since this is a post about proxy misspecification, I'm implicitly screening off these concerns and imagining that proxy misspecification is the only obstruction to alignment.