A few notes/questions about things that seem like errors in the paper (or maybe I'm confused — anyway, none of this invalidates any conclusions of the paper, but if I'm right or at least justifiably confused, then these do probably significantly hinder reading the paper; I'm partly posting this comment to possibly prevent some readers in the future from wasting a lot of time on the same issues):
1) The formula for here seems incorrect:
This is because W_i is a feature corresponding to the i'th coordinate of x (this is not evident from the screenshot, but it is evident from the rest of the paper), so surely what shows up in this formula should not be W_i, but instead the i'th row of the matrix which has columns W_i (this matrix is called W later). (If one believes that W_i is a feature, then one can see this is wrong already from the dimensions in the dot product not matching.)
2) Even though you say in the text at the beginning of Section 3 that the input features are independent, the first sentence below made me make a pragmatic inference that you are not assuming that the coordinates are independent for this particular claim about how the loss simplifies (in part because if you were assuming independence, you could replace the covariance claim with a weaker variance claim, since the 0 covariance part is implied by independence):
However, I think you do use the fact that the input features are independent in the proof of the claim (at least you say "because the x's are independent"):

Additionally, if you are in fact just using independence in the argument here and I'm not missing something, then I think that instead of saying you are using the moment-cumulants formula here, it would be much much better to say that independence implies that any term with an unmatched index is . If you mean the moment-cumulants formula here https://en.wikipedia.org/wiki/Cumulant#Joint_cumulants , then (while I understand how to derive every equation of your argument in case the inputs are independent), I'm currently confused about how that's helpful at all, because one then still needs to analyze which terms of each cumulant are 0 (and how the various terms cancel for various choices of the matching pattern of indices), and this seems strictly more complicated than problem before translating to cumulants, unless I'm missing something obvious.
3) I'm pretty sure this should say x_i^2 instead of x_i x_j, and as far as I can tell the LHS has nothing to do with the RHS:
(I think it should instead say sth like that the loss term is proportional to the squared difference between the true and predictor covariance.)

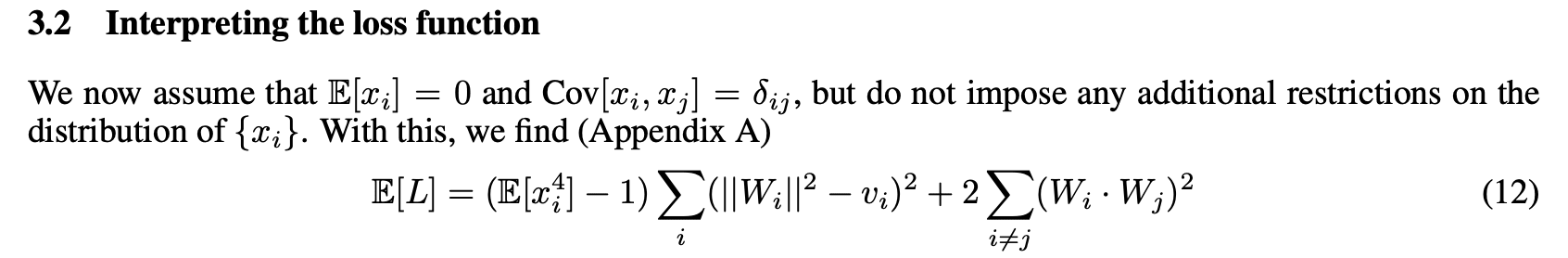

(For context: My guess is that by default, humans get disempowered by AIs (or maybe a single AI) and the future is much worse than it could be, and in particular is much worse than a future where we do something like slowly and thoughtfully growing ever more intelligent ourselves instead of making some alien system much smarter than us any time soon.)
Given that you seem to think alignment of AI systems with developer intent happens basically by default at this point, I wonder what you think about the following:
(The point of the hypothetical is to investigate the difficulty of intent alignment at the relevant level of capability, so if it seems to you like it's getting at something quite different, then I've probably failed at specifying a good hypothetical. I offer some clarifications of the setup in the appendix that may or may not save the hypothetical in that case.)
My sense is that humanity is not remotely on track to be able to make such an AI in time. Imo by default, any superintelligent system we could make any time soon would minimally end up doing all sorts of other stuff and in particular would not follow the suicide directive.
If your response is "ok maybe this is indeed quite cursed but that doesn't mean it's hard to make an AI that takes over and has Human Values and serves as a guardian who also cures cancer and maybe makes very many happy humans and maybe ends factory farming and whatever" then I premove the counter-response "hmm well we could discuss that hope but wait first: do you agree that you just agreed that intent alignment is really difficult at the relevant capability level?".
If your response is "no this seems pretty easy actually" then I should argue against that but I'm not going to premove that counter-response.
Appendix: some clarifications on the hypothetical