This is a linkpost for our two recent papers:

1. An exploration of using degeneracy in the loss landscape for interpretability https://arxiv.org/abs/2405.10927
2. An empirical test of an interpretability technique based on the loss landscape https://arxiv.org/abs/2405.10928

This work was produced at Apollo Research in collaboration with Kaarel Hanni (Cadenza Labs), Avery Griffin, Joern Stoehler, Magdalena Wache and Cindy Wu. Not to be confused with Apollo's recent Sparse Dictionary Learning paper.

A key obstacle to mechanistic interpretability is finding the right representation of neural network internals. Optimally, we would like to derive our features from some high-level principle that holds across different architectures and use cases. At a minimum, we know two things:

1. We know that the training loss goes down during training. Thus, the features learned during training must be determined by the loss landscape. We want to use the structure of the loss landscape to identify what the features are and how they are represented.
2. We know that models generalize, i.e. that they learn features from the training data that allow them to accurately predict on the test set. Thus, we want our interpretation to explain this generalization behavior.

Generalization has been linked to basin broadness in the loss landscape in several ways, most notably including singular learning theory, which introduces the learning coefficient as a measure of basin broadness that doubles as a measure of generalization error that replaces the parameter count in Occam's razor.

Inspired by both of these ideas, the first paper explores using the structure of the loss landscape to find the most computationally natural representation of a network. We focus on identifying parts of the network that are not responsible for low loss (i.e. degeneracy), inspired by singular learning theory. These degeneracies are an obstacle for interpretability as they mean there exist parameters which do not affect the input-output behavior in the network (similar to the parameters of a Transformer $W_V$ and $W_O$ matrices that do not affect the product $W_{OV}$).

We explore 3 different ways neural network parameterisations can be degenerate:

1. when activations are linearly dependent
2. when gradient vectors are linearly dependent
3. when ReLU neurons fire on the same inputs.

This investigation leads to the interaction basis, and eventually the local interaction basis (LIB) that we test in the second paper. This basis removes computationally irrelevant features and interactions, and sparsifies the remaining  interactions between layers. 

Finally, we analyse how modularity is connected to degeneracy in the loss landscape. We suggest a preliminary metric for finding the sorts of modules that the neural network prior is biased towards.

The second paper tests how useful the LIB is in toy and language models. In this new basis we calculate integrated gradient based interactions between features, and analyse the graph of all features in a network. We interpret strongly-interacting features, and identify modules in this graph using the modularity metric of the first paper.

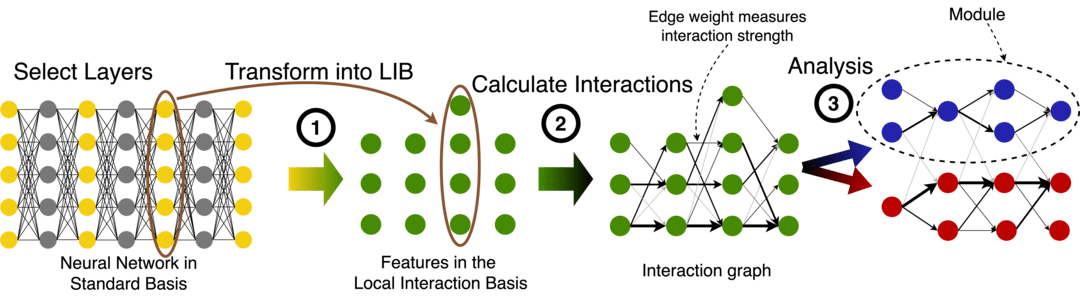
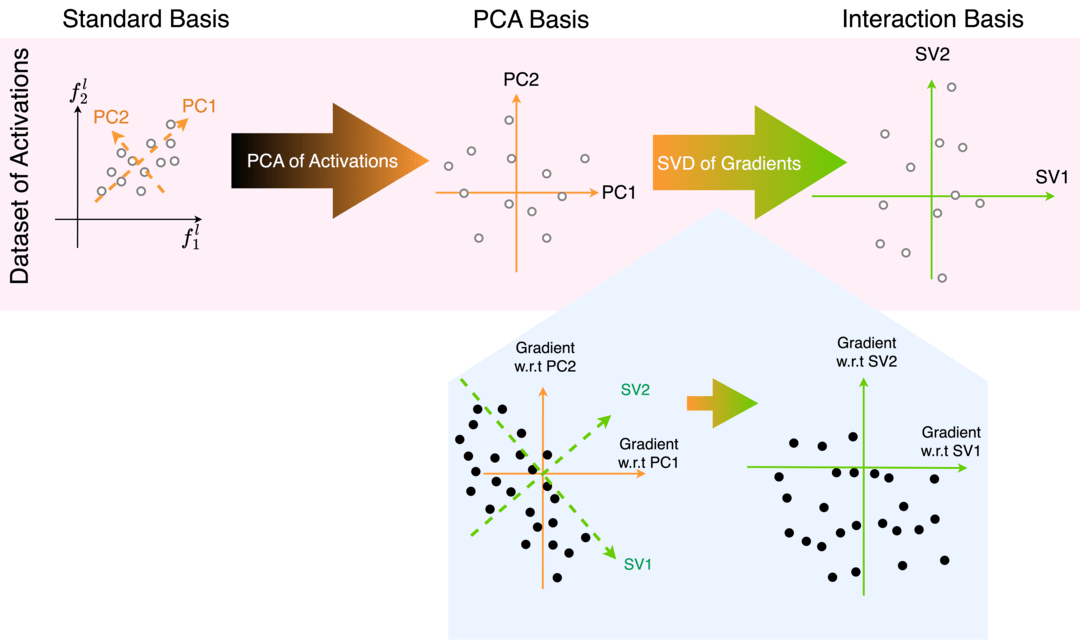
To derive the LIB basis we coordinate-transform the activations of neural networks in two steps: Step 1 is a transformation into the PCA basis, removing activation space directions which don't explain any variance. Step 2 is a transformation of the activations to align the basis with the right singular vectors of the gradient vector dataset. The 2nd step is the key new ingredient which aims to make interactions between adjacent layers sparse, and removes directions which do not affect downstream computation.

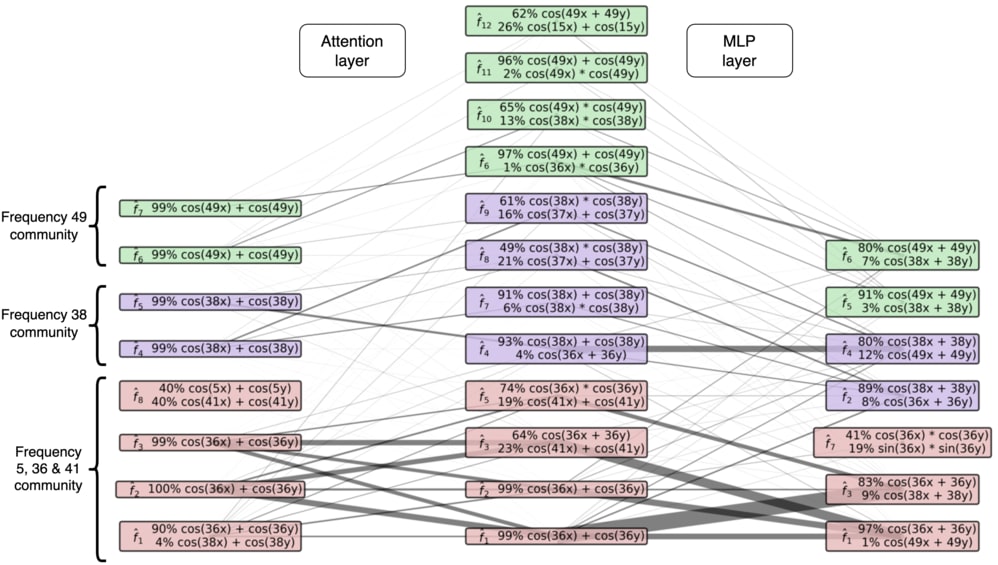
We test LIB on two toy models (modular addition & CIFAR-10), and two language models (Tinystories-1M & GPT2-small). On toy models we successfully find a basis that is more sparsely interacting and contains only computationally-relevant features, and we can identify circuits based on the interaction graphs. See the interaction graph for the modular addition transformer below (cherry picked result).

On language models however, we find that LIB does not help us understand the networks. We find that interaction sparsity, compared to a PCA baseline, increases only slightly (for Tinystories-1M) or not at all (GPT2-small), and can identify no modules or interpretable features.

While this is mostly a negative result, we think there is valuable future work to develop loss landscape inspired techniques for interpretability that makes fewer assumptions than those that went into the derivation of LIB. Most notably, in deriving LIB, we did not assume superposition to be true because we wanted to start with the simplest possible version of the theory, and because we wanted to make a bet that was decorrelated with other research in the field. However, recent advances in sparse dictionary learning suggests that work which relaxes the assumptions of LIB to allow for superposition may find more interpretable features.