On $b_{\text{mag}}$, it's unclear what a "natural" choice would be for setting this parameter in order to simplify the architecture further. One natural reference point is to set it to $e^{r_{\text{mag}}}\odot b_{\text{gate}}$, but this corresponds to getting rid of the discontinuity in the Jump ReLU (turning the magnitude encoder into a ReLU on multiplicatively rescaled gate encoder preactivations). Effectively (removing the now unnecessary auxiliary task), this would give results similar to the "baseline + rescale & shift" benchmark in section 5.2 of the paper, although probably worse, as we wouldn't have the shift.

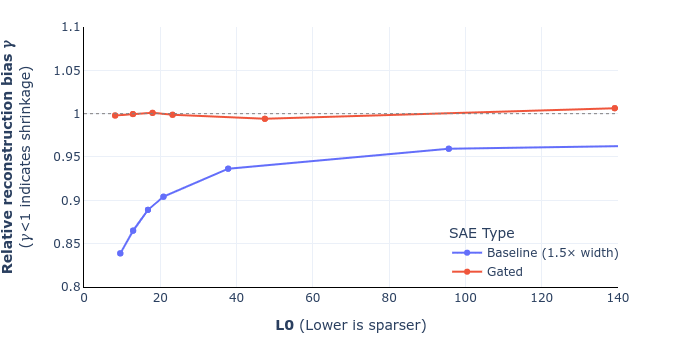
UPDATE: we've corrected equations 9 and 10 in the paper (screenshot of the draft below) and also added a footnote that hopefully helps clarify the derivation. I've also attached a revised figure 6, showing that this doesn't change the overall story (for the mathematical reasons I mentioned in my previous comment). These will go up on arXiv, along with some other minor changes (like remembering to mention SAEs' widths), likely some point next week. Thanks again Sam for pointing this out!

Updated equations (draft):

Updated figure 6 (shrinkage comparison for GELU-1L):

Yep, the intuition here indeed was that L1 penalised reconstruction seems to be okay for teaching a standard SAE's encoder to detect which features are on (even if features get shrunk as a result), so that is effectively what this auxiliary loss is teaching the gate sub-layer to do, alongside the sparsity penalty. (The key difference being we freeze the decoder in the auxiliary task, which the ablation study shows helps performance.) Maybe to put it another way, this was an auxiliary task that we had good evidence would teach the gate sublayer to detect active features reasonably well, and it turned out to give good results in practice. It's totally possible though that there are better auxiliary tasks (or even completely different loss functions) out there that we've not explored.

Hey Sam, thanks - you're right. The definition of reconstruction bias is actually the argmin of

$$E[|\hat{x}/{\gamma }^{\prime }-x{|}^2]$$

which I'd (incorrectly) rearranged as the expression in the paper. As a result, the optimum is

$${\gamma }^{-1}=E[\hat{x}\cdot x]/E\left[|\hat{x}{|}^2\right]$$

That being said, the derivation we gave was not quite right, as I'd incorrectly substituted the optimised loss rather than the original reconstruction loss, which makes equation (10) incorrect. However the difference between the two is small exactly when gamma is close to one (and indeed vanishes when there is no shrinkage), which is probably why we didn't pick this up. Anyway, we plan to correct these two equations and update the graphs, and will submit a revised version.