Interesting post, thanks for writing it!
I think that the QK section somewhat under-emphasises the importance of the softmax. My intuition is that models rarely care about as precise a task as counting the number of pairs of matching query-key features at each pair of token positions, and that instead softmax is more of an "argmax-like" function that finds a handful of important token positions (though I have not empirically tested this, and would love to be proven wrong!). This enables much cheaper and more efficient solutions, since you just need the correct answer to be the argmax-ish.
For example, ignoring floating point precision, you can implement a duplicate token head with and arbitrarily high . If there are vocab elements, map the th query and key to the point of the way round the unit circle. The dot product is maximised when they are equal.
If you further want the head to look at a resting position unless the duplicate token is there, you can increase , and have a dedicated BOS dimension with a score of , so you only get a higher score for a perfect match. And then make the softmax temperature super low so it's an argmax.
Thanks for the comment!
In more detail:
In our discussion of softmax (buried in part 1 of section 4), we argue that our story makes the most sense precisely when the temperature is very low, in which case we only attend to the key(s) that satisfy the most skip feature-bigrams. Also, when features are very sparse, the number of skip feature bigrams present in one query-key pair is almost always 0 or 1, and we aren't trying to super precisely track whether its, say, 34 or 35.
I agree that if softmax is just being an argmax, then one implication is that we don't need error terms to be , instead, they can just be somewhat less than 1. However, at least in our general framework, this doesn't help us beyond changing the log factor in the tilde inside ). There still will be some log factor because we require the average error to be to prevent the worst-case error being greater than 1. Also, we may want to be able to accept 'ties' in which a small number of token positions are attended to together. To achieve this (assuming that at most one SFB is present for each QK pair for simplicity) we'd want the variation in the values which should be 1 to be much smaller than the gap between the smallest value which should be 1 and the largest value which should be 0.
A few comments about your toy example:
To tell a general story, I'd like to replace the word 'token' with 'feature' in your construction. In particular, I might want to express what the attention head does using the same features as the MLP. The choice of using tokens in your example is special, because the set of features {this is token 1, this is token 2, ...} are mutually exclusive, but once I allow for the possibility that multiple features can be present (for example if I want to talk in terms of features involved in MLP computation), your construction breaks. To avoid this problem, I want the maximum dot product between f-vectors to be at most 1/(the maximum number of features that can be present at once). If I allow several features to be present at once, this starts to look like an -orthogonal basis again. I guess you could imagine a case where the residual stream is divided into subspaces, and inside each subspace is a set of mutually exclusive features (à la tegum products of TMS). In your picture, there would need to be a 2d subspace allocated to the 'which token' features anyway. This tegum geometry would have to be specifically learned — these orthogonal subspaces do not happen generically, and we don't see a good reason to think that they are likely to be learned by default for reasons not to do with the attention head that uses them, even in the case that there are these sets of mutually exclusive features.
It takes us more than 2 dimensions, but in our framework, it is possible to do a similar construction to yours in dimensions assuming random token vectors (ie without the need for any specific learned structure in the embeddings for this task): simply replace the rescaled projection matrix with where is and is a projection matrix to a -dimensional subspace. Now, with high probability, each vector has a larger dot product with its own projection than another vector's projection (we need to be this large to ensure that projected vectors all have a similar length). Then use the same construction as in our post, and turn the softmax temperature down to zero.
Someone suggested this comment was inscrutable so here's a summary:
I don't think that how argmax-y softmax is being is a crux between us - we think our picture makes the most sense when softmax acts like argmax or top-k so we hope you're right that softmax is argmax-ish. Instead, I think the property that enables your efficient solution is that the set of features 'this token is token (i)' is mutually exclusive, ie. only one of these features can activate on an input at once. That means that in your example you don't have to worry about how to recover feature values when multiple features are present at once. For more general tasks implemented by an attention head, we do need to worry about what happens when multiple features are present at the same time, and then we need the f-vectors to form a nearly orthogonal basis and your construction becomes a special case of ours I think.
Haven't read everything yet, but that seems like excellent work. In particular, I think this general research avenue is extremely well-motivated.
Figuring out how to efficiently implement computations on the substrate of NNs had always seemed like a neglected interpretability approach to me. Intuitively, there are likely some methods of encoding programs into matrix multiplication which are strictly ground-truth better than any other encoding methods. Hence, inasmuch as what the SGD is doing is writing efficient programs on the NN substrate, it is likely doing so by making use of those better methods. And so nailing down the "principles of good programming" on the NN substrate should yield major insights regarding how the naturally-grown NN circuits are shaped as well.
This post seems to be a solid step in that direction!
(I haven't had the chance to read part 3 in detail, and I also haven't checked the proofs except insofar as they seem reasonable on first viewing. Will probably have a lot more thoughts after I've had more time to digest.)
This is very cool work! I like the choice of U-AND task, which seems way more amenable to theoretical study (and is also a much more interesting task) than the absolute value task studied in Anthropic's Toy Model of Superposition (hereafter TMS). It's also nice to study this toy task with asymptotic theoretical analysis as opposed to the standard empirical analysis, thereby allowing you to use a different set of tools than usual.
The most interesting part of the results was the discussion on the universality of universal calculation -- it reminds me of the interpretations of the lottery ticket hypothesis that claim some parts of the network happen to be randomly initialized to have useful features at the start.
Some examples that are likely to be boolean-interpretable are bigram-finding circuits and induction heads. However, it's possible that most computations are continuous rather than boolean[31].
My guess is that most computations are indeed closer to continuous than to boolean. While it's possible to construct boolean interpretations of bigram circuits or induction heads, my impression (having not looked at either in detail on real models) is that neither of these cleanly occur inside LMs. For example, induction heads demonstrate a wide variety of other behavior, and even on induction-like tasks, often seem to be implementing induction heuristics that involve some degree of semantic content.
Consequently, I'd be especially interested in exploring either the universality of universal calculation, or the extension to arithmetic circuits (or other continuous/more continuous models of computation in superposition).
Some nitpicks:
The post would probably be a lot more readable if it were chunked into 4. The 88 minute read time is pretty scary, and I'd like to comment only on the parts I've read.
Section 2:
Two reasons why this loss function might be principled are
- If there is reason to think of the model as a Gaussian probability model
- If we would like our loss function to be basis independent
A big reason to use MSE as opposed to eps-accuracy in the Anthropic model is for optimization purposes (you can't gradient descent cleanly through eps-accuracy).
Section 5:
4 How relevant are our results to real models?
This should be labeled as section 5.
Appendix to the Appendix:
Here, $f_i$ always denotes the vector.
[..]
with \[\sigma_1\leq n\) with
(TeX compilation failure)
Thanks for the kind feedback!
I'd be especially interested in exploring either the universality of universal calculation
Do you mean the thing we call genericity in the further work section? If so, we have some preliminary theoretical and experimental evidence that genericity of U-AND is true. We trained networks on the U-AND task and the analogous U-XOR task, with a narrow 1-layer MLP and looked at the size of the interference terms after training with a suitable loss function. Then, we reinitialised and froze the first layer of weights and biases, allowing the network only to learn the linear readoff directions, and found that the error terms were comparably small in both cases.
This figure is the size of the errors for (which is pretty small) for readoffs which should be zero in blue and one in yellow (we want all these errors to be close to zero).
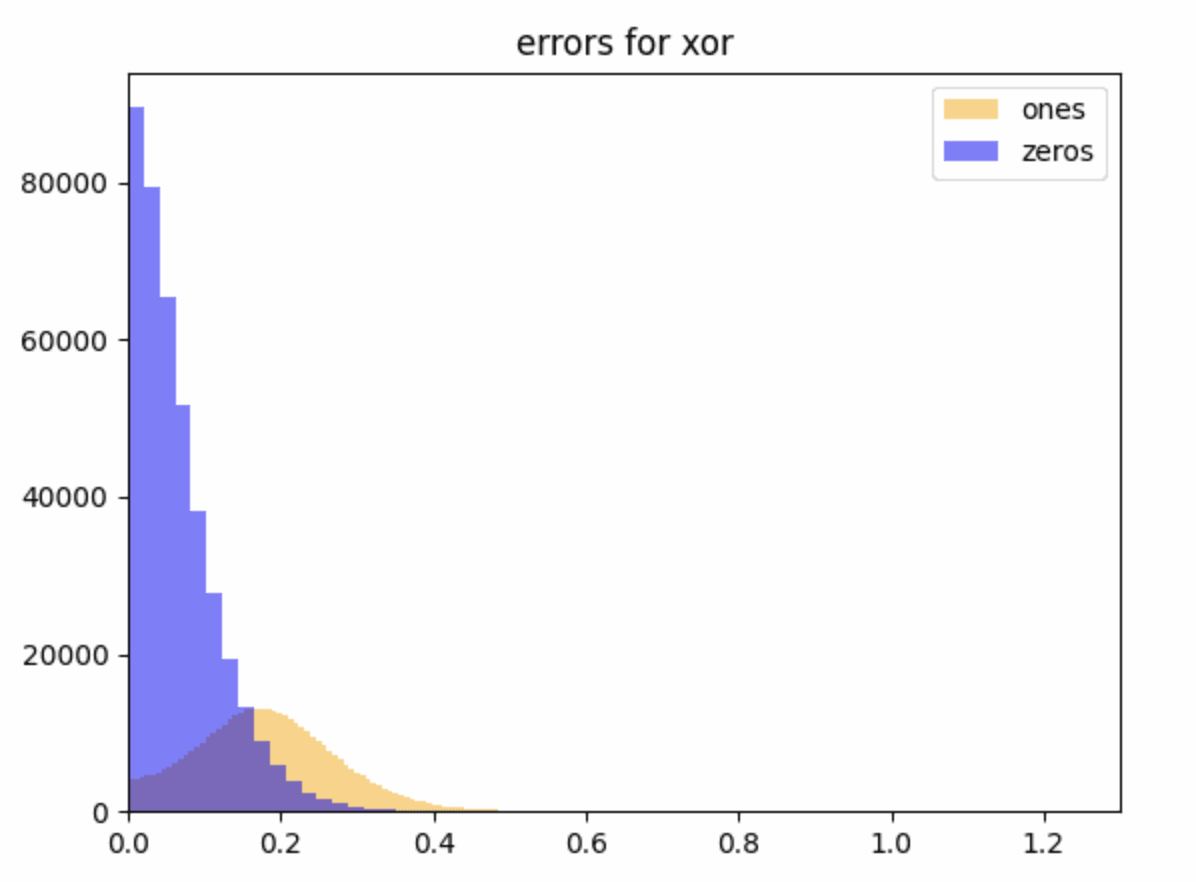
This suggests that the AND/XOR directions were -linearly readoffable at initialisation, but the evidence at this stage is weak because we don't have a good sense yet of what a reasonable value of is for considering the task to have been learned correctly: to answer this we want to fiddle around with loss functions and training for longer. For context, an affine readoff (linear + bias) directly on the inputs can read off with , which has an error of . This is larger than all but the largest errors here, and you can’t do anything like this for XOR with affine readoff.
After we did this, Kaarel came up with an argument that networks randomly initialised with weights from a standard Gaussian and zero bias solve U-AND with inputs not in superposition (although it probably can be generalised to the superposition case) for suitable readoffs. To sketch the idea:
Let be the vector of weights from the th input to the neurons. Then consider the linear readoff vector with th component given by:
where is the indicator function. There are 4 free parameters here, which are set by 4 constraints given by requiring that the expectation of this vector dotted with the activation vector has the correct value in the 4 cases . In the limit of large the value of the dot product will be very close to its expectation and we are done. There are a bunch of details to work out here and, as with the experiments, we aren't 100% sure the details all work out, but we wanted to share these new results since you asked.
A big reason to use MSE as opposed to eps-accuracy in the Anthropic model is for optimization purposes (you can't gradient descent cleanly through eps-accuracy).
We've suggested that perhaps it would be more principled to use something like loss for larger than 2, as this is closer to -accuracy. It's worth mentioning that we are currently finding that the best loss function for the task seems to be something like with extra weighting on the target values that should be . We do this to avoid the problem that if the inputs are sparse, then the ANDs are sparse too, and the model can get good loss on (for low ) by sending all inputs to the zero vector. Once we weight the ones appropriately, we find that lower values of may be better for training dynamics.
or the extension to arithmetic circuits (or other continuous/more continuous models of computation in superposition)
We agree and are keen to look into that!
(TeX compilation failure)
Thanks - fixed.
How are you setting when ? I might be totally misunderstanding something but at - feels like you need to push up towards like 2k to get something reasonable? (and the argument in 1.4 for using clearly doesn't hold here because it's not greater than for this range of values).
Author order randomized. Authors contributed roughly equally — see attribution section for details.
Update as of July 2024: we have collaborated with @LawrenceC to expand section 1 of this post into an arXiv paper, which culminates in a formal proof that computation in superposition can be leveraged to emulate sparse boolean circuits of arbitrary depth in small neural networks.
What kind of document is this?
What you have in front of you is so far a rough writeup rather than a clean text. As we realized that our work is currently highly relevant to recent questions posed by interpretability researchers, we put together a lightly edited version of private notes we've written over the last ~4 months. If you'd be interested in writing up a cleaner version, get in touch, or just do it. We're making these notes public before we're done with the project because of some combination of (1) seeing others think along similar lines and wanting to make it less likely that people (including us) spend time duplicating work, (2) providing a frame which we think provides plenty of concrete immediate problems for people to independently work on[1] (3) seeking feedback to decrease the chance we spend a bunch of time on nonsense.
1 minute summary
Superposition is a mechanism that might allow neural networks to represent the values of many more features than they have neurons, provided that those features are present sparsely in the dataset. However, until now, an understanding of how computation can be done in a compressed way directly on these stored features has been limited to a few very specific tasks (for example here). The goal of this post is to lay the groundwork for a picture of how computation in superposition can be done in general. We hope this will enable future research to build interpretability techniques for reverse engineering circuits that are manifestly in superposition.
Our main contributions are:
10 minute summary
Thanks to Nicholas Goldowsky-Dill for producing an early version of this summary/diagrams and generally for being instrumental in distilling this post.
Central to our analysis of MLPs is the Universal-AND (U-AND) problem:
This problem is central to understanding computation in superposition because:
If m=d0 (the dimension of the input space), then we can store the input features using an orthonormal basis such as the neuron basis. A naive solution in this case would be to have one neuron per pair which is active if both inputs are true and 0 otherwise. This requires (m2)=Θ(d20) neurons, and involves no superposition:
On this input x1,x2 and x5 are true, and all other inputs are false.
We can do much better than this, computing all the pairwise ANDs up to a small error with many fewer neurons. To achieve this, we have each neuron care about a random subset of inputs, and we choose the bias such that each neuron is activated when at least two of them are on. This requires d=Θ(polylog(d)) neurons: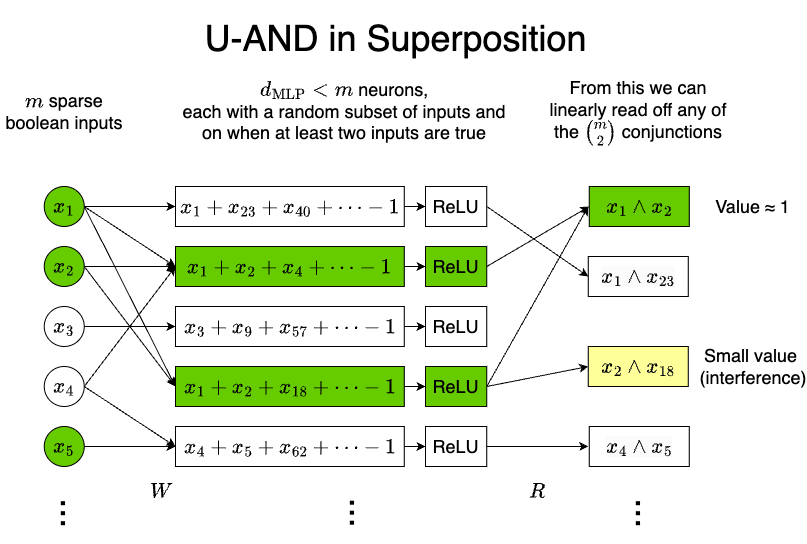
Importantly:
Our analysis of the QK part of an attention head centers on the task of skip feature-bigram checking:
This framing is valuable for understanding the role played by the attention mechanism in superposed computation because:
A nice way to construct WQK is as a sum of terms for each skip feature-bigram, each of which is a rank one matrix equal to outer product of the two feature vectors in the SFB. In the case that all feature vectors are orthogonal (no superposition) you should be thinking of something like this:
where each of the rank one matrices, when multiplied by a residual stream vector on the right and left, performs a dot product on each side:
→aTsWQK→at=∑i(→as⋅→fki)(→fqi⋅→at)
where (fk1,fq1),…,(fk|B|,fq|B|) are the feature bigrams in B with feature directions (→fki,→fqi), and →as is a residual stream vector at sequence position s. Each of these rank one matrices contributes a value of 1 to the value of →aTsWQK→at if and only if the corresponding SFB is present. Since the matrix cannot be higher rank than dhead, typically we can only check for up to ~Θ(dhead) SFBs this way.
In fact we can check for many more SFBs than this, if we tolerate some small error. The construction is straightforward once we think of WQK as this sum of tensor products: we simply add more rank one matrices to the sum, and then approximate the sum as a rank dhead matrix, using the SVD or even a random projection matrix P. This construction can be easily generalised to the case that the residual stream stores features in superposition (provided we take care to manage the size of the interference terms) in which case WQK can be thought of as being constructed like this:
When multiplied by a residual stream vector on the right and left, this expression is →aTsWQK→at=∑i(→as⋅→fki)(P→fqi⋅→at)
Importantly:
Indeed, there are many open directions for improving our understanding of computation in superposition, and we’d be excited for others to do future research (theoretical and empirical) in this area.
Some theoretical directions include:
Empirical directions include:
Structure of the Post
In Section 1, we define the U-AND task precisely, and then walk through our construction and show that it solves the task. Then we generalise the construction in 2 important ways: in Section 1.1, we modify the construction to compute ANDs of input features which are stored in superposition, allowing us to stack multiple U-AND layers together to simulate a boolean circuit. In Section 1.2 we modify the construction to compute ANDs of more than 2 variables at the same time, allowing us to compute all sufficiently small[4] boolean functions of the inputs with a single MLP. Then in Section 1.3 we explore efficiency gains from replacing the ReLU with a quadratic activation function, and explore the consequences.
In Section 2 we explore a series of questions around how to interpret the maths in Section 1, in the style of FAQs. Each part of Section 2 is standalone and can be skipped, but we think that many of the concepts discussed there are valuable and frequently misunderstood.
In section 3 we turn to the QK circuit, carefully introducing the skip feature-bigram checking task, and we explain our construction. We also discuss two scenarios that allow for more SFBs to be checked for than the simplest construction would allow.
We discuss the relevance of our constructions to real models in Section 4, and conclude in Section 5 with more discussion on Open Directions.
Notation and Conventions
In this post we make extensive use of Big-O notation and its variants, little o, Θ,Ω,ω. See wikipedia for definitions. We also make use of tilde notation, which means we ignore log factors. For example, by saying a function f(n) is Θ(g(n)), we mean that there are nonzero constants c1,c2>0 and a natural number N such that for all n>N, we have c1g(n)≤f(n)≤c2g(n). By saying a quantity is ~Θ(f(d)), we mean that this is true up to a factor that is a polynomial of logd — i.e., that it is asymptotically between f(d)/polylog(d) and f(d)polylog(d).
1 The Universal AND
We introduce a simple and central component in our framework, which we call the Universal AND component or U-AND for short. We start by introducing the most basic version of the problem this component solves. We then provide our solution to the simplest version of this problem. We later discuss a few generalizations: to inputs which store features in superposition, and to higher numbers of inputs to each AND gate. More elaboration on U-AND — in particular, addressing why we think it’s a good question to ask — is provided in Section 2.
1.1 The U-AND task
The basic boolean Universal AND problem: Given an input vector which stores an orthogonal set of boolean features, compute a vector from which can be linearly read off the value of every pairwise AND of input features, up to a small error. You are allowed to use only a single-layer MLP and the challenge is to make this MLP as narrow as possible.
More precisely: Fix a small parameter ϵ>0 and let d0 and ℓ be integers with d0≥ℓ[7]. Let →e1,…,→ed0 be the standard basis in Rd0, i.e. →ei is the vector whose ith component is 1 and whose other components are 0. Inputs are all at most ℓ-composite vectors, i.e., for each index set I⊆[d] with |I|≤ℓ, we have the input →xI=∑i∈I→ei∈Rd0. So, our inputs are in bijection with binary strings that contain at most ℓ ones[8]. Our task is to compute all (d02) pairwise ANDs of these input bits, where the notion of ‘computing’ a property is that of making it linearly represented in the output activation vector →a(→x)∈Rd. That is, for each pair of inputs i,j, there should be a linear function ri,j:Rd→R, or more concretely, a vector →ri,j∈Rd, such that →rTi,j→a(x)≈ϵANDi,j(x). Here, the ≈ϵ indicates equality up to an additive error ϵ and ANDi,j is 1 iff both bits i and j of x are 1. We will drop the subscript ϵ going forward.
We will provide a construction that computes these Θ(d20) features with a single d-neuron ReLU layer, i.e., a d0×d matrix W and a vector →b∈Rd such that →a(x)=ReLU(W→x+→b), with d≪d0. Stacking the readoff vectors →ri,j we provide as the rows of a readout matrix R, you can also see us as providing a parameter setting solving −−−−→ANDs(→x)≈ϵR(ReLU(W→x+→b)), where −−−−→ANDs(→x) denotes the vector of all (d02) pairwise ANDs. But we’d like to stress that we don’t claim there is ever something like this large, size (d02), layer present in any practical neural net we are trying to model. Instead, these features would be read in by another future model component, like how the components we present below (in particular, our U-AND construction with inputs in superposition and our QK circuit) do.
There is another kind of notion of a set of features having been computed, perhaps one that’s more native to the superposition picture: that of the activation vector (approximately) being a linear combination of f-vectors — we call these vectors f-vectors— corresponding to these properties, with coefficients that are functions of the values of the features. We can also consider a version of the U-AND problem that asks for output vectors which represent the set of all pairwise ANDs in this sense, maybe with the additional requirement that the f-vectors be almost orthogonal. Our U-AND construction solves this problem, too — it computes all pairwise ANDs in both senses. See the appendix for a discussion of some aspects of how the linear readoff notion of stuff having been computed, the linear combination notion of something having been computed, and almost orthogonality hang together.
1.2 The U-AND construction
We now present a solution to the U-AND task, computing (d02) new features with an MLP width that can be much smaller than (d02). We will go on to show how our solution can be tweaked to compute ANDs of more than 2 features at a time, and to compute ANDs of features which are stored in superposition in the inputs.
To solve the base problem, we present a random construction: W (with shape d0×d) has entries that are iid random variables which are 1 with probability p(d)≪1, and each entry in the bias vector is −1. We will pin down what p should be later.
We will denote by Si the set of neurons that are ‘connected’ to the ith input, in the sense that elements of the set are neurons for which the ith entry of the row of the weight vector that connects to that neuron is 1. →Si is used to denote the indicator set of Si: the vector which is 1 for every neuron in Si and 0 otherwise. So →Si is also the ith column of W.
Then we claim that for this choice of weight matrix, all the ANDs are approximately linearly represented in the MLP activation space with readoff vectors (and feature vectors, in the sense of Appendix B) given by
v(xi∧xj)=vij=−−−−−→Si∩Sj|Si∩Sj|
for all i,j, where we continue our abuse of notation to write Si∩Sj as shorthand for the vector which is an indicator for the intersection set, and |Si∩Sj| is the size of the set.
We preface our explanation of why this works with a technical note. We are going to choose d and p (as functions of d0) so that with high probability, all sets we talk about have size close to their expectation. To do this formally, one first shows that the probability of each individual set having size far from its expectation is smaller than any 1/poly(d0) using the Chernoff bound (Theorem 4 here), and one follows this by a union bound over all only poly(d0) sets to say that with probability 1−o(1), none of these events happen. For instance, if a set Si∩Sj has expected size log4d0, then the probability its size is outside of the range log4d0±log3d0 is at most 2e−μδ2/3=2e−log2d0=2ed−logd00 (following these notes, we let μ denote the expectation and δ denote the number of μ-sized deviations from the expectation — this bound works for δ<1 which is the case here). Technically, before each construction to follow, we should list our parameters d,p and all the sets we care about (for this first construction, these are the double and triple intersections between the Si) and then argue as described above that with high probability, they all have sizes that only deviate by a factor of 1+o(1) from their expected size and always carry these error terms around in everything we say, but we will omit all this in the rest of the U-AND section.
So, ignoring this technicality, let’s argue that the construction above indeed solves the U-AND problem (with high probability). First, note that |Si∩Sj|∼Bin(d,p2). We require that p is big enough to ensure that all intersection sets are non-empty with high probability, but subject to that constraint we probably want p to be as small as possible to minimise interference[9]. We'll choose p=log2d0/√d, such that the intersection sets have size |Si∩Sj|≈log4d0. We split the check that the readoff works out into a few cases:
So we see that this readoff is indeed the AND of i and j up to error ϵ=O(1/log2d0).
To finish, we note without much proof that everything is also computed in the sense that 'the activation vector is a linear combination of almost orthogonal features' (defined in Appendix B). The activation vector being an approximate linear combination of pairwise intersection indicator vectors with coefficients being given by the ANDs follows from triple intersections being small, as does the almost-orthogonality of these feature vectors.
U-AND allows for arbitrary XORs to be efficiently calculated
A consequence of the precise (up to ϵ) nature of our universal AND is the existence of a universal XOR, in the sense of every XOR of features being computed. In this post by Sam Marks, it is tentatively observed that real-life transformers linearly compute XOR of arbitrary features in the weak sense of being able to read off tokens where XOR of two tokens is true using a linear probe (not necessarily with ϵ accuracy). This weak readoff behavior for AND would be unsurprising, as the residual stream already has this property (using the readoff vector →fi+→fj which has maximal value if and only if fi and fj are both present). However, as Sam Marks observes, it is not possible to read off XOR in this weak way from the residual stream. We can however see that such a universal XOR (indeed, in the strong sense of ϵ-accuracy) can be constructed from our strong (i.e., ϵ-accurate) universal AND. To do so, assume that in addition to the residual stream containing feature vectors →fi and →fj, we’ve also already almost orthogonally computed universal AND features →fANDi,j into the residual stream. Then we can weakly (and in fact, ϵ-accurately) read off XOR from this space by taking the dot product with the vector →fXORi,j:=→fi+→fj−2→fANDi,j. Then we see that if we had started with the two-hot pair →fi′+→fj′, the result of this readoff will be, up to a small error O(ϵ),
⎧⎨⎩0=0−0,|{i,j}∩{i′,j′}|=0(neither coefficient agrees)1=1−0,|{i,j}∩{i′,j′}|=1(one coefficient agrees)0=2−2,{i,j}={i′,j′}(both coefficients agree)
This gives a theoretical feasibility proof of an efficiently computable universal XOR circuit, something Sam Marks believed to be impossible.
1.3 Handling inputs in superposition: sparse boolean computers
Any boolean circuit can be written as a sequence of layers executing pairwise ANDs and XORs[11] on the binary entries of a memory vector. Since our U-AND can be used to compute any pairwise ANDs or XORs of features, this suggests that we might be able to emulate any boolean circuit by applying something like U-AND repeatedly. However, since the outputs of U-AND store features in superposition, if we want to pass these outputs as inputs to a subsequent U-AND circuit, we need to work out the details of a U-AND construction that can take in features in superposition. In this section we explore the subtleties of modifying U-AND in this way. In so doing, we construct an example of a circuit which acts entirely in superposition from start to finish — nowhere in the construction are there as many dimensions as features! We consider this to be an interesting result in its own right.
U-ANDs ability to compute many boolean functions of inputs features stored in superposition provides an efficient way to use all the parameters of the neural net to compute (up to a small error) a boolean circuit with a memory vector that is wider than the layers of the NN[12]. We call this emulating a ‘boolean computer’. However, three limitations prevent any boolean circuit from being computed:
Therefore, the boolean circuits we expect can be emulated in superposition (1) are sparse circuits (2) have few layers (3) have memory vectors which are not larger than the square of the activation space dimension.
Construction details for inputs in superposition
Now we generalize U-AND to the case where input features can be in superposition. With f-vectors →f1,…,→fm∈Rd0, we give each feature a random set of neurons to map to, as before. After coming up with such an assignment, we set the ith row of W to be the sum of the f-vectors for features which map to the ith neuron. In other words, let F be the m×d0 matrix with ith row given by the components of →fi in the neuron basis:
F=⎛⎜ ⎜ ⎜⎝→f1→⋮→fm→⎞⎟ ⎟ ⎟⎠
Now let \hat{W} be a sparse matrix (with shape d×m) with entries that are iid Bernoulli random variables which are 1 with probability p(d)≪1. Then:
W=^WF
Unfortunately, since the →f1,…,→fm are random vectors, their inner product will have a typical size of 1/√d0. So, on an input which has no features connected to neuron i, the preactivation for that neuron will not be zero: it will be a sum of these interference terms, one for each feature that is connected to the neuron. Since the interference terms are uncorrelated and mean zero, they start to cause neurons to fire incorrectly when Θ(d0) neurons are connected to each neuron. Since each feature is connected to each neuron with probability p=log2d0√d) this means neurons start to misfire when m=~Θ(d0√d)[13]. At this point, the number of pairwise ANDs we have computed is (m2)=~Θ(d20d).
This is a problem, if we want to be able to do computation on input vectors storing potentially exponentially many features in superposition, or even if we want to be able to do any sequential boolean computation at all:
Consider an MLP with several layers, all of width dMLP, and assume that each layer is doing a U-AND on the features of the previous layer. Then if the features start without superposition, there are initially dMLP features. After the first U-AND, we have Θ(d2MLP) new features, which is already too many to do a second U-AND on these features!
Therefore, we will have to modify our goal when features are in superposition. That said, we're not completely sure there isn't any modification of the construction that bypasses such small polynomial bounds. But e.g. one can't just naively make ^W sparser — p can't be taken below d−1/2 without the intersection sets like |Si∩Sj| becoming empty. When features were not stored in superposition, solving U-AND corresponded to computing d20 many new features. Instead of trying to compute all pairwise ANDs of all (potentially exponentially many) input features in superposition, perhaps we should try to compute a reasonably sized subset of these ANDs. In the next section we do just that.
A construction which computes a subset of ANDs of inputs in superposition
Here, we give a way to compute ANDs of up to d0d particular feature pairs (rather than all (m2) ANDs) that works even for m that is superpolynomial in d0[14]. (We’ll be ignoring log factors in much of what follows.)
In U-AND, we take ^W to be a random matrix with iid 0/1 entries with probability p=log2d0√d. If we only need/want to compute a subset of all the pairwise ANDs — let E be this set of all pairs of inputs {i,j} for which we want to compute the AND of i and j — then whenever {i,j}∈E, we might want each pair of corresponding entries in the corresponding columns i and j of the adjacency matrix ^W, i.e., each pair (^W)ki, (^W)kj to be a bit more correlated than an analogous pair in column i′ and j′ with {i′,j′}∉E. Or more precisely, we want to make such pairs of columns {i,j} have a surprisingly large intersection for the general density of the matrix — this is to make sure that we get some neurons which we can use to read off the AND of {i,j}, while choosing the general density in ^W to be low enough that we don’t cross the density threshold at which a neuron needs to care about too many input features.
One way to do this is to pick a uniformly random set of log4d0 neurons for each {i,j}∈E, and to set the column of ^W corresponding to input i to be the indicator vector of the union of these sets (i.e., just those assigned to gates involving i). This way, we can compute up to around |E|=~Θ(d0d) pairwise ANDs without having any neuron care about more than d0 input features, which is the requirement from the previous section to prevent neurons misfiring when input f-vectors are random vectors in superposition with typical interference size Θ(1/√d0).
1.4 ANDs with many inputs: computation of small boolean circuits in a single layer
It is known that any boolean circuit with k inputs can be written as a linear combination (with possibly exponential in k terms, which is a substantial caveat) ANDs with up to k inputs (fan-in up to k)[15]. This means that, if we can compute not just pairwise ANDs, but ANDs of all fan-ins up to k, then we can write down a ‘universal’ computation that computes (simultaneously, in a linearly-readable sense) all possible circuits that depend on some up to k inputs.
The U-AND construction for higher fan-in
We will modify the standard, non-superpositional U-AND construction to allow us to compute all ANDs of a specific fan-in k.
We'll need two modifications:
Now we read off the AND of a set I of input features along the vector ⋂i∈ISi.
We can straightforwardly simultaneously compute all ANDs of fan-ins ranging from 2 to k by just evenly partitioning the d neurons into k−1 groups — let’s label these 2,3,…,k — and setting the weights into group i and the biases of group i as in the fan-in i U-AND construction.
A clever choice of density can give us all the fan-ins at once
Actually, we can calculate all ANDs of up to some constant fan-ink in a way that feels more symmetric than the option involving a partition above[16] by reusing the fan-in 2 U-AND with (let’s say) d=d0 and a careful choice of p=1log2d0 . This choice of p is larger than log2d0d1/k for any k, ensuring that every intersection set is non-empty. Then, one can read off ANDi,j from Si∩Sj as usual, but one can also read off ANDi,j,k with the composite vector
−Si∩Sj∩Sk|Si∩Sj∩Sk|+Si∩Sj|Si∩Sj|+Si∩Sk|Si∩Sk|+Sj∩Sk|Sj∩Sk| In general, one can read off the AND of an index set I with the vector ∑I′⊆I s.t. |I′|≥2(−1)|I|−|I′|+1vI′ where vI′=⋂i∈I′Si∣∣⋂i∈I′Si∣∣One can show that this inclusion-exclusion style formula works by noting that if the subset of indices of I which are on is J, then the readoff will be approximately ∑I′⊆I s.t. |I′|≥2(−1)|I|−|I′|+1max(0,|I′∩J|−1). We’ll leave it as an exercise to show that this is 0 if J≠I and 1 if J=I.
Extending the targeted superpositional AND to other fan-ins
It is also fairly straightforward to extend the construction for a subset of ANDs when inputs are in superposition to other fan-ins, doing all fan-ins on a common set of neurons. Instead of picking a set for each pair that we need to AND as above, we now pick a set for each larger AND gate that we care about. As in the previous sparse U-AND, each input feature gets sent to the union of the sets for its gates, but this time, we make the weights depend on the fan-in. Letting K denote the max fan-in over all gates, for a fan-in k gate, we set the weight from each input to K/k, and set the bias to −K+1. This way, still with at most about ~Θ(d2) gates, and at least assuming inputs have at most some constant number of features active, we can read the output of a gate off with the indicator vector of its set.
1.5 Improved Efficiency with a Quadratic Nonlinearity
It turns out that, if we use quadratic activation functions x↦x2 instead of ReLU's x↦ReLU(x), we can write down a much more efficient universal AND construction. Indeed, the ReLU universal AND we constructed can compute the universal AND of up to ~Θ(d3/2) features in a d-dimensional residual stream. However, in this section we will show that with a quadratic activation, for ℓ-composite vectors, we can compute all pairwise ANDs of up to m=Ω(exp(12ℓϵ2√d))[17] features stored in superposition (this is exponential in √d, so superpolynomial in d(!)) that admit a single-layer universal AND circuit.
The idea of the construction is that, on the large space of features Rm, the AND of the boolean-valued feature variables fi,fj can be written as a quadratic function qi,j:{0,1}m↦{0,1}; explicitly, qi,j(f1,…,fm)=fi⋅fj. Now if we embed feature space Rm onto a smaller Rr in an ϵ-almost-orthogonal way, it is possible to show that the quadratic function qi,j on Rm is well-approximated on sparse vectors by a quadratic function on Rr (with error bounded above by 2ϵ on 2-sparse inputs in particular). Now the advantage of using quadratic functions is that any quadratic function on Rr can be expressed as a linear read-off of a special quadratic function Q:Rr→Rr2 given by the composition of a linear function Rr→Rr2 and a quadratic element-wise activation function on Rr2 which creates a set of neurons which collectively form a basis for all quadratic functions. Now we can set d=r2 to be the dimension of the residual stream and work with an r-dimensional subspace V of the residual stream, taking the almost-orthogonal embedding Rm→V. Then the map VQ→Rd provides the requisite universal AND construction. We make this recipe precise in the following section
Construction Details
In this section we use slightly different notation to the rest of the post, dropping overarrows for vectors, and we drop the distinction between features and f-vectors.
Let V=Rr be as above. There is a finite-dimensional space of quadratic functions on Rr, with basis qij=xixj of size r2 (such that we can write every quadratic function as a linear combination of these basis functions); alternatively, we can write qij(v)=(v⋅ei)(v⋅ej), for ei,ej the basis vectors. We note that this space is spanned by a set of functions which are squares of linear functions of {xi}:
L(1)i(x1,…,xr)=xiL(2)i,j(x1,…,xr)=xi+xjL(3)i,j(x1,…,xr)=xi−xj
The squares of these functions are a valid basis for the space of quadratic functions on Rr since qii=(L(1)i)2 and for i≠j, we have qij=(L(2)i,j)2−(L(3)i,j)24. There are m distinct functions of type (1), and (m2) functions each of type (2) and (3), for a total of r2 basis functions as before. Thus there exists a single-layer quadratic-activation neural net Q:x↦y from Rr→Rr2 such that any quadratic function on Rr is realizable as a "linear read-off", i.e., given by composing Q with a linear function Rr2→R. In particular, we have linear "read-off" functions Λij:Rr2→R such that Lij(Q(x))=qij(x).
Now suppose that f1,…,fm is a collection of f-vectors which are ϵ-almost-orthogonal, i.e., such that |fi|=1 for any i and |fi⋅fj|<ϵ∀i<j≤m. Note that (for fixed ϵ<1), there exist such collections with exponential (in r) number of vectors m. We can define a new collection of symmetric bilinear functions (i.e., functions in two vectors v,w∈Rn which are linear in each input independently and symmetric to switching v,w), ϕi,j, for a pair of (not necessarily distinct) indices 0<i≤j≤m, defined by ϕi,j(v)=(v⋅fi)(v⋅fj) (this is a product of two linear functions, hence quadratic). We will use the following result:
Proposition 1 Suppose ϕi,j is as above and 0<i′≤j′<m is another pair of (not necessarily distinct) indices associated to feature vectors vi,vj. Then
ϕi,j(vi′,vj′)⎧⎨⎩=1,i=i′ and j=j′∈(−ϵ,ϵ),(i,j)≠(i′,j′)∈(−ϵ2,ϵ2),{i,j}∩{i′,j′}=∅ (i.e., no indices in common)
This proposition follows immediately from the definition of ϕk,ℓ and the almost orthogonality property. □
Now define the single-valued quadratic function ϕsinglei,j(v):=12ϕi,j(v,v), by applying the bilinear form to two copies of the same vector and dividing by 2. Then the proposition above implies that, for two pairs of distinct indices 0<i<j≤m and 0<i′<j′≤m we have the following behavior on the sum of two features (the superpositional analog of a two-hot vector):
ϕsinglei,j(vi′+vj′)=ϕi,j(vi′,vi′)+2ϕi,j(vi′,vj′)+ϕi,j(vj′,vj′)2=ϕi,j(vi′,vj′)+O(ϵ).
The first formula follows from bilinearity (which is equivalent to the statement that the two entries in ϕi,j behave distributively) and the last formula follows from the proposition since we assumed (i,j) are distinct indices, hence cannot match up with a pair of identical indices (i′,i′) or (j′,j′). Moreover, O(ϵ) term in the formula above is bounded in absolute value by 2ϵ2=ϵ.
Combining this formula with Proposition 1, we deduce:
Proposition 2
ϕsinglei,j(vi′+vj′)=⎧⎨⎩1+O(ϵ),i=i′ and j=j′O(ϵ),(i,j)≠(i′,j′)O(ϵ2),i≠i′.
Moreover, by the triangle inequality, the linear constants inherent in the O(...) notation are ≤2. □
Corollary ϕi,j(vi′+vj′)=δ(i,j),(i′,j′)+O(ϵ), where the δ notation returns 1 when the two pairs of indices are equal and 0 otherwise.
We can now write down the universal AND function by setting d=r2 above. Assume we have m<exp(ϵ22r). This guarantees (with probability approaching 1) that m random vectors in V≅Rr are (ϵ-)almost orthogonal, i.e., have dot products <ϵ. We assume the vectors v1,…,vm are initially embedded in V⊂Rd. (Note that we can instead assume they were initially randomly embedded in Rd, then re-embedded in Rr by applying a random projection and rescaling appropriately.) Let Q:Rr→Rd=r2 be the universal quadratic map as above; we let qij:Rd→R be the quadratic functions as above. Now we claim that Q is a universal AND with respect to the feature vectors v1,…,vN. Note that, since the function ϕsinglei,j(v) is quadratic on Rr, it can be factorized as ϕsinglei,j(x)=Φi,j(Q(x)), for Φi,j some linear function on Rr2[18]. We now see that the linear maps Φi,j are valid linear read-offs for ANDs of features: indeed,
Φi,j(Q(vi′+vj′))=ϕsinglei,j(vi′,vj′)=δ(i,j),(i′,j′)+O(ϵ)=AND(bi′,j′i,bi′,j′j),
where bi′,j′ is the two-hot boolean indicator vector with 1s in positions i′ and j′. Thus the AND of any two indices i,j can be computed via the readout linear function Φi,j on any two-hot input bi′,j′. Moreover, applying the same argument to a larger sparse sum gives Φi,j(Q(∑mk=1bkvk))=AND(bi,bj)+O(s2ϵ), where s=∑mk=1bk is the sparsity[19].
Scaling and comparison with ReLU activations
It is surprising that the universal AND circuit we wrote down for quadratic activations is so much more expressive than the one we have for ReLU activations, since the conventional wisdom for neural nets is that the expressivity of different (suitably smooth) activation functions does not increase significantly when we replace arbitrary activations by quadratic ones. We do not know if this is a genuine advantage of quadratic activations over others (and indeed might be implemented in transformers in some sophisticated way involving attention nonlinearities), or whether there is some yet-unknown reason that (perhaps assuming nice properties of our features), ReLU's can give more expressive universal AND circuits than we have been able to find in the present work. We list this discrepancy as an interesting open problem that follows from our work.
Generalizations
Note that the nonlinear function Q above lets us read off not only the AND of two sparse boolean vectors, but more generally the sum of products of coordinates of any sufficiently sparse linear combination of feature vectors vi (not necessarily boolean). More generally, if we replace quadratic activations with cubic or higher, we can get cubic expressions, such as the sum of triple ANDs (or, more generally, products of triples of coordinates). A similar effect can be obtained by chaining l sequential levels of quadratic activations to get polynomial nonlinearities with exponent e=2l. Then so long as we can fit O(re)[20] features in the residual stream in an almost-orthogonal way (corresponding to a basis of monomials of degree d on r-dimensional space), we can compute sums of any degree-e monomial over features, and thus any boolean circuit of degree e, up to O(ϵ), where the linear constant implicit in the O depends on the exponent e. This implies that for any value e, there is a dimension d universal nonlinear map Rd→Rd with ⌈log2(e)⌉ quadratic activations such that any sparse boolean circuit involving ≤e elements is linearly represented (via an appropriate readoff vector). Moreover, keeping e fixed, d grows only as O(log(n))e. However, the constant associated with the big-O notation might grow quite quickly as the exponent e increases. It would be interesting to analyse this scaling behavior more carefully, but that is outside the scope of the present work.
1.6 Universal Keys: an application of parallel boolean computation
So far, we have used our universal boolean computation picture to show that superpositional computation in a fully-connected neural network can be more efficient (specifically, compute roughly as many logical gates as there are parameters rather than non-superpositional implementations, which are bounded by number of neurons). This does not fully use the universality of our constructions: i.e., we must at every step read a polynomial (at most quadratic) number of features from a vector which can (in either the fan-in-k or quadratic-activation contexts) compute a superpolynomial number of boolean circuits. At the same time, there is a context in transformers where precisely this universality can give a remarkable (specifically, superpolynomial in certain asymptotics) efficiency improvement. Namely, recall that the attention mechanism of a transformer can be understood as a way for the last-token residual stream to read information from past tokens which pass a certain test associated to the query-key component. In our simplified boolean model, we can conceptualize this as follows:
Importantly, there is an information asymmetry between the “past” tokens (which contribute the key) and the last token that implements the linear read-off via query: in generating the boolean relevance function, the past token can use information that is not accessible to the token generating the key (as it is in its “future” – this is captured e.g. by the attention mask). One might previously have assumed that in generating a key vector, tokens need to “guess” which specific combinations of key features may be relevant to future tokens, and separately generate some read-off for each; this limits the possible expressivity of choosing the relevance function g to a small (e.g. linear in parameter number) number of possibilities.
However, our discovery of circuits that implement universal calculation suggests a surprising way to resolve this information asymmetry: namely, using a universal calculation, the key can simultaneously compute, in an approximately linearly-readable way, ALL possible simple circuits of up to Olog(dresid) inputs. This increases the number of possibilities of the relevance function g to allow all such simple circuits; this can be significantly larger than the number of parameters and asymptotically (for logarithmic fan-ins) will in fact be superpolynomial[21]. As far as we are aware, this presents a qualitative (from a complexity-theoretic point of view) update to the expressivity of the attention mechanism compared to what was known before.
Sam Marks’ discovery of the universal XOR was done in this context: he observed using a probe that it is possible for the last token of a transformer to attend to past tokens that return True as the XOR of an arbitrary pair of features, something that he originally believed was computationally infeasible.
We speculate that this will be noticeable in real-life transformers, and can partially explain the observation that transformers tend to implement more superposition than fully-connected neural networks.
2 U-AND: discussion
We discuss some conceptual matters broadly having to do with whether the formal setup from the previous section captures questions of practical interest. Each of these subsections is standalone, and you needn’t read any to read Section 3.
Aren't the ANDs already kinda linearly represented in the U-AND input?
This subsection refers to the basic U-AND construction from Section 1.1, with inputs not in superposition, but the objection we consider here could also be raised against other U-AND variants. The objection is this: aren’t ANDs already linearly present in the input, so in what sense have we computed them with the U-AND? Indeed, if we take the dot product of a particular 2-hot input with (→ei+→ej)/2, we get 0 if neither the ith nor the jth features are present, 1/2 if 1 of them is present, and 1 if they are both present. If we add a bias of −1/4, then without any nonlinearity at all, we get a way to read off pairwise U-AND for ϵ=1/4. The only thing the nonlinearity lets us do is to reduce this “interference” ϵ=1/4 to a smaller ϵ. Why is this important?
In fact, one can show that you can't get more accurate than ϵ=1/4 without a nonlinearity, even with a bias, and ϵ=1/4 is not good enough for any interesting boolean circuit. Here’s an example to illustrate the point:
Suppose that I am interested in the variable z=∧(xi,xj)+∧(xk,xl). z takes on a value in {0,1,2} depending on whether both, one, or neither of the ANDs are on. The best linear approximation to z is 1/2(xi+xj+xk+xl−1), which has completely lost the structure of z. In this case, we have lost any information about which way the 4 variables were paired up in the ANDs.
In general, computing a boolean expression with k terms without the signal being drowned out by the noise will require ϵ<1/k if the noise is correlated, and ϵ<1/k2 if the noise is uncorrelated. In other words, noise reduction matters! The precision provided by ϵ-accuracy allows us to go from only recording ANDs to executing more general circuits in an efficient or universal way. Indeed, linear combinations of linear combinations just give more linear combinations – the noise reduction is the difference between being able to express any boolean function and being unable to express anything nonlinear at all. The XOR construction (given above) is another example that can be expressed as a linear combination involving the U-AND and would not work without the nonlinearity.
Aren’t the ANDs already kinda nonlinearly represented in the U-AND input?
This subsection refers to the basic U-AND construction from Section 1.1, with inputs not in superposition, but the objection we consider here could also be raised against other U-AND variants. While one cannot read off the ANDs linearly before the ReLU, except with a large error, one could certainly read them off with a more expressive model class on the activations. In particular, one can easily read ANDi,j off with a ReLU probe, by which we mean ReLU(rTx+b), with r=ei+ej and b=−1. We think there’s some truth to this: we agree that if something can be read off with such a probe, it’s indeed at least almost already there. And if we allowed multi-layer probes, the ANDs would be present already when we only have some pre-input variables (that our input variables are themselves nonlinear functions of). To explore a limit in ridiculousness: if we take stuff to be computed if it is recoverable by a probe that has the architecture of GPT-3 minus the embed and unembed and followed by a projection on the last activation vector of the last position residual stream, then anything that is linearly accessible in the last layer of GPT-3 is already ‘computed’ in the tuple of input embeddings. And to take a broader perspective: any variable ever computed by a deterministic neural net is in fact a function of the input, and is thus already ‘there in the input’ in an information-theoretic sense (anything computed by the neural net has zero conditional entropy given the input). The information about the values of the ANDs is sort of always there, but we should think of it as not having been computed initially, and as having been computed later[22].
Anyway, while taking something to be computed when it is affinely accessible seems natural when considering reading that information into future MLPs, we do not have an incredibly strong case that it’s the right notion. However, it seems likely to us that once one fixes some specific notion of stuff having been computed, then either exactly our U-AND construction or some minor variation on it would still compute a large number of new features (with more expressive readoffs, these would just be more complex properties — in our case, boolean functions of the inputs involving more gates). In fact, maybe instead of having a notion of stuff having been computed, we should have a notion of stuff having been computed for a particular model component, i.e. having been represented such that a particular kind of model component can access it to ‘use it as an input’. In the case of transformers, maybe the set of properties that have been computed as far as MLPs can tell is different than the set of properties that have been computed as far as attention heads (or maybe the QK circuit and OV circuit separately) can tell. So, we’re very sympathetic to considering alternative notions of stuff having been computed, but we doubt U-AND would become much less interesting given some alternative reasonable such notion.
If you think all this points to something like it being weird to have such a discrete notion of stuff having been computed vs not at all, and that we should maybe instead see models as ‘more continuously cleaning up representations’ rather than performing computation: while we don’t at present know of a good quantitative notion of ‘representation cleanliness’, so we can’t at present tell you that our U-AND makes amount x of representation cleanliness progress and x is sort of large compared to some default, it does seem intuitively plausible to us that it makes a good deal of such progress. A place where linear read-offs are clearly qualitatively important and better than nonlinear read-offs is in application to the attention mechanism of a transformer.
Does our U-AND construction really demonstrate MLP superposition?
This subsection refers to the basic U-AND construction from Section 1.1, with inputs not in superposition, but the objection we consider here could also be raised against other U-AND variants. One could try to tell a story that interprets our U-AND construction in terms of the neuron basis: we can also describe the U-AND as approximately computing a family of functions each of which record whether at least two features are present out of a particular subset of features[23]. Why should we see the construction as computing outputs into superposition, instead of seeing it as computing these different outputs on the neurons? Perhaps the 'natural' units for understanding the NN is in terms of these functions, as unintuitive as they may seem to a human.
In fact, there is a sense in which if one describes the sampled construction in the most natural way it can be described in the superposition picture, one needs to spend more bits than if one describes it in the most natural way it can be described in this neuron picture. In the neuron picture, one needs to specify a subset of size ~Θ(d0/√d) for each neuron, which takes dlog2(d0~Θ(d0/√d))≤~Θ(d20√d) bits to specify. In the superpositional picture, one needs to specify (d02) subsets of size ~Θ(1), which takes about ~Θ(d20) bits to specify[24]. If, let’s say, d=d0, then from the point of view of saving bits when representing such constructions, we might even prefer to see them in a non-superpositional manner!
We can imagine cases (of something that looks like this U-AND showing up in a model) in which we’d agree with this counterargument. For any fixed U-AND construction, we could imagine a setup where for each neuron, the inputs feeding into it form some natural family — slightly more precisely, that whether two elements of this family are present is a very natural property to track. In fact, we could imagine a case where we perform future computation that is best seen as being about these properties computed by the neurons — for instance, our output of the neural net might just be the sum of the activations of these neurons. For instance, perhaps this makes sense because having two elements of one of these families present is necessary and sufficient for an image to be that of a dog. In such a case, we agree it would be silly to think of the output as a linear combination of pairwise AND features.
However, we think there are plausible contexts in which such a circuit would show up in which it seems intuitively right to see the output as a sparse sum of pairwise ANDs: when the families tracked by particular neurons do not seem at all natural and/or when it is reasonable to see future model components as taking these pairwise AND features as inputs. Conditional on thinking that superposition is generic, it seems fairly reasonable to think that these latter contexts would be generic.
Is universal calculation generic?
The construction of the universal AND circuit in the “quadratic nonlinearity” section above can be shown to be stable to perturbations; a large family of suitably “random” circuits in this paradigm contain all AND computations in a linearly-readable way. This updates us to suspect that at least some of our universal calculation picture might be generic: i.e., that a random neural net, or a random net within some mild set of conditions (that we can’t yet make precise), is sufficiently expressive to (weakly) compute any small circuit. Thus linear probe experiments such as Sam Marks’ identification of the “universal XOR” in a transformer may be explainable as a consequence of sufficiently complex, “random-looking” networks. This means that the correct framing for what happens in a neural net executing superposition might not be that the MLP learns to encode universal calculation (such as the U-AND circuit), but rather that such circuits exist by default, and what the neural network needs to learn is, rather, a readoff vector for the circuit that needs to be executed. While we think that this would change much of the story (in particular, the question of “memorization” vs. “generalization” of a subset of such boolean circuit features would be moot if general computation generically exists), this would not change the core fact that such universal calculation is possible, and therefore likely to be learned by a network executing (or partially executing) superposition. In fact, such an update would make it more likely that such circuits can be utilized by the computational scheme, and would make it even more likely that such a scheme would be learned by default.
We hope to do a series of experiments to check whether this is the case: whether a random network in a particular class executes universal computation by default. If we find this is the case, we plan to train a network to learn an appropriate read-off vector starting from a suitably random MLP circuit, and, separately, to check whether existing neural networks take advantage of such structure (i.e., have features – e.g. found by dictionary learning methods – which linearly read off the results of such circuits). We think this would be particularly productive in the attention mechanism (in the context of “universal key” generation, as explained above).
What are the implications of using ϵ-accuracy? How does this compare to behavior found by minimizing some loss function?
A specific question here is:
The answer is that sometimes they are not going to be the same. In particular, our algorithm may not be given a low loss by MSE. Nevertheless, we think that ϵ-accuracy is a better thing to study for understanding superposition than MSE or other commonly considered loss functions (cross entropy would be much less wise than either!) This point is worth addressing properly, because it has implications for how we think about superposition and how we interpret results from the toy models of superposition paper and from sparse autoencoders, both of which typically use MSE.
For our U-AND task, we ask for a construction →f(→x) that approximately equals a 1-hot target vector →y, with each coordinate allowed to differ from its target value by at most epsilon. A loss function which would correspond to this task would look like a cube well with vertical sides (the inside of the region L∞(→f(→x),→y)<ϵ). This non-differentiable loss function would be useless for training. Let’s compare this choice to alternatives and defend it.
If we know that our target is always a 1-hot vector, then maybe we should have a softmax at the end of the network and use cross-entropy loss. We purposefully avoid this, because we are trying to construct a toy model of the computation that happens in intermediate layers of a deep neural network, taking one activation vector to a subsequent activation vector. In the process there is typically no softmax involved. Also, we want to be able to handle datapoints in which more than 1 AND is present at a time: the task is not to choose which AND is present, but *which of the ANDs* are present.
The other ubiquitous choice of loss function is MSE. This is the loss function used to evaluate model performance in two tasks that are similar to U-AND: the toy model of superposition and SAEs. Two reasons why this loss function might be principled are
We see no reason to assume the former here, and while the latter is a nice property to have, we shouldn’t expect basis independence here: we would like the ANDs to be computed in a particular basis and are happy with a loss function that privileges that basis.
Our issue with MSE (and Lp in general for finite p) can be demonstrated with the following example:
Suppose the target is y=(1,0,0,…). Let ^y=(0,0,…) and ~y=(1+ϵ,ϵ,ϵ,…), where all vectors are (d02)-dimensional. Then ||y−^y||p=1 and ||y−~y||p=(d02)1/pϵ. For large enough (d02)>ϵ−p, the latter loss is larger than 1[25]. Yet intuitively, the latter model output is likely to be a much better approximation to the target value, from the perspective of the way the activation vector will be used for subsequent computation. Intuitively, we expect that for the activation vector to be good enough to trigger the right subsequent computation, it needs to be unambiguous whether a particular AND is present, and the noise in the value needs to be below a certain critical scale that depends on the way the AND is used subsequently, to avoid noise drowning out signal. To understand this properly we’d like a better model of error propagation.
It is no coincidence that our U-AND algorithm may be ϵ-accurate for small ϵ, but is not a minimum of the MSE. In general, ϵ-accuracy permits much more superposition than minimising the MSE, because it penalises interference less.
For a demonstration of this, consider a simplified toy model of superposition with hidden dimension d and inputs which are all 1-hot unit vectors. We consider taking the limit as the number of input features goes to infinity and ask: what is the optimum number N(d) of inputs that the model should store in superposition, before sending the rest to the zero vector?
If we look for ϵ-accurate reconstruction, then we know how to answer this: a random construction allows us to fit at least Nϵ(d)=Cexpϵ2d vectors into d-dimensional space.
As for the algorithm that minimises the MSE reconstruction loss (ie not sent to the zero vector in the hidden space), consider that we have already put n of the inputs into superposition, and we are trying to decide whether it is a good idea to squeeze another one in there. Separating the loss function into reconstruction terms and interference terms (as in the original paper):
So, the optimum number of features to store can be found by asking when the contribution to the loss ℓ(n+1)∼nδ(n)2−1 switches from negative to positive, so we need an estimate of δ(n). If feature vectors are chosen randomly, then δ(n)2=O(1/d) and we find that the optimal number of features to store is O(d). In fact, feature vectors are chosen to minimise interference, which allows us to fit a few more feature vectors in (the advantage this gives us is most significant at small n) before the accumulating interferences become too large, and empirically we observe that the optimal number of features to store is NL2(d)=O(dlogd). This is much much less superposition that we are allowed with ϵ-accurate reconstruction!
See the figure below for experimental values of NLp(d) for a range of p,d. We conjecture that for each p,NLp(d) is the minimum of an exponential function which is independent of p and something like a polynomial which depends on p.
3 The QK part of an attention head can check for many skip feature-bigrams, in superposition
In this section, we present a story for the QK part of an attention head which is analogous to the MLP story from the previous section. Note that although both focus on the QK component, this is a different (though related) story to the story about universal keys from section 1.4.
We begin by specifying a simple task that we think might capture a large fraction of the role performed by the QK part of an attention head. Roughly, the task (analogous to the U-AND task for the MLP) is to check for the presence of one in a large set of ‘skip bigrams’[26] of features[27].
We’ll then provide a construction of the QK part of an attention head that can perform this task in a superposed manner — i.e., a specification of a low-rank matrix WQK=WTKWQ that checks for a given set of skip feature-bigrams. A naive construction could only check for dhead feature bigrams; ours can check for ~Θ(dheaddresid) feature bigrams. This construction is analogous to our construction solving the targeted superpositional AND from the previous sections.
3.1 The skip feature-bigram checking task
Let B be a set of ‘skip feature-bigrams’; each element of B is a pair of features (→fi,→fj)∈Rdresid×Rdresid. Let’s define what we mean by a skip feature-bigram being present in a pair of residual stream positions. Looking at residual stream activation vectors just before a particular attention head (after layernorm is applied), we say that the activation vectors →as,→at∈Rdresid at positions s,t contain the skip feature-bigram (→fi,→fj) if feature →fi is present in →at and feature →fj is present in →as. There are two things we could mean by the feature →fi being present in an activation vector →a. The first is that →fi⋅→a′ is always either ≈0 or ≈1 for any a′ in some relevant data set of activation vectors, and →fi⋅→a=1. The second notion assumes the existence of some background set →f1,→f2,…,→fm in terms of which each activation vector a has a given background decomposition, a=∑mi=1ci→fi. In fact, we assume that all ci∈{0,1}, with at most some constant number of ci=1 for any one activation vector, and we also assume that the →fi are random vectors (we need them to be almost orthogonal). The second notion guarantees the first but with better control on the errors, so we’ll run with the second notion for this section[28].
Plausible candidates for skip feature-bigrams (→fi,→fj) to check for come from cases where if the query residual stream vector has feature →fj, then it is helpful to do something with the information at positions where →fi is present. Here are some examples of checks this can capture:
The task is to use the attention score S (the attention pattern pre-softmax) to count how many of these conditions are satisfied by each choice of query token position and key token position. That is, we’d like to construct a low-rank bilinear form WTKWQ such that the (s,t) entry of the attention score matrix Sst=→aTsWTKWQ→at contains the number of conditions in C which are satisfied for the query residual stream vector in token position s and the key residual stream vector in the token position t. We'll henceforth refer to the expression WTKWQ as WQK, a matrix of size dresid×dresid that we choose freely to solve the task subject to the constraint that its rank is at most dhead<dresid. If each property is present sparsely, then most conditions are not satisfied for most positions in the attention score most of the time.
We will present a family of algorithms which allow us to perform this task for various set sizes |B|. We will start with a simple case without superposition analogous to the 'standard' method for computing ANDs without superposition. Unlike for U-AND though, the algorithm for performing this task in superposition is a generalization of the non-superpositional case. In fact, given our presentation of the non-superpositional case, this generalization is fairly immediate, with the main additional difficulty being to keep track of errors from approximate calculations.
3.2 A superposition-free algorithm
Let’s make the assumption that m is at most dresid. For the simplest possible algorithm, let’s make the further (definitely invalid) assumption that the feature basis is the neuron basis. This means that →as is a vector in {0,1}dresid. In the absence of superposition, we do not require that these features are sparse in the dataset.
To start, consider the case where B contains only one feature bigram (→ei,→ej). The task becomes: ensure that Sst=→aTsWQK→at is 1 if feature →fi is present in→as and feature →fj is present in →at and 0 otherwise. The solution to this task is to choose WQK to be a matrix with zero everywhere except in the i,j component: (WQK)kl=δkiδlj —with this matrix, →aTsWQK→at=1 iff the i entry of →as is 1 and the j entry of →at is 1. Note that we can write WQK=→k⊗→q where →k=→ei, →q=→ej, and ⊗ denotes the outer product/tensor product/Kronecker product. This expression makes it manifest that WQK is rank 1. Whenever we can decompose a matrix into a tensor product of two vectors (this will prove useful), we will call it a _pure tensor_ in accordance with the literature. Note that this decomposition allows us to think of WQK in terms of the query part and key part separately: first we project the residual stream vector in the query position onto the ith feature vector which tells us if feature i is present at the query position, then we do the same for the key, and then we multiply the results.
In the next simplest case, we take the set B to consist of pairs (ei,ej). To solve the task for this B, we can simply perform a sum over WPQK for each bigram in B, since there is no interference. That is, we choose
WPQK=∑(i,j)∈B→ei⊗→ej
The only new subtlety that is introduced in this modification comes from the requirement that the rank of WPQK be at most dhead which won't be true in general. The rank of WPQK is not trivial to calculate for a given B. This is because we can factorize terms in the sum:
→ej1⊗→ei1+→ej1⊗→ei2+→ej2⊗→ei1+→ej2⊗→ei2=(→ej1+→ej2)⊗(→ei1+→ei2)
which is a pure tensor. The rank requirement is equivalent to the statement that WPKW can contain at most dhead terms _after maximum factorisation_ (a priori, not necessarily in terms of such pure tensors of sums of subsets of basis vectors). Visualizing the set B as a bipartite graph with m nodes on the left and right, we notice that pure tensors correspond to any subgraphs of B that are _complete_ bipartite subgraphs (cliques). A sufficient condition for the rank of W being at most dhead is if the edges of B can be partitioned into at most dhead cliques. Thus, whether we can check for all feature bigrams in B this way depends not only on the size of B, but also its structure.. In general, we can’t use this construction to guarantee that we can check for more than dhead skip feature-bigrams.
Generalizing our algorithm to deal with the case when the feature basis is not neuron-aligned (although it is still an orthogonal basis) could not be simpler. All we do is replace {→ei} with the new feature basis, use the same expression for WPQK, and we are done.
3.3 Checking for a structured set of skip feature-bigrams with activation superposition
We now consider the case where the residual stream contains m>dresid sparsely activated features stored in superposition. We'll assume that the feature vectors are random unit vectors, and we'll switch notation from e1,…,edresid to f1,…,fm from now on to emphasize that the f-vectors are not an orthogonal basis. We'd like to generalize the superposition-free algorithm to the case when the residual stream vector stores features in superposition, but to do so, we'll have to keep track of the interference between non-orthogonal f-vectors. We know that the root mean square dot product between two f-vectors is 1/√dresid. Every time we check for a bigram that isn't present and pick up an interference term, the noise accumulates - for the signal to beat the noise here, we need the sum of interference terms to be less than 1. We’ll ignore log factors in the rest of this section.
We'll assume that most of the interference comes from checking for bigrams (→fi,→fj) where →fi isn’t in →as and also →fj isn’t in →at — that cases where one feature is present but not the other are rare enough to contribute less can be checked later. These pure tensors typically contribute an interference of 1/dresid. We can also consider the interference that comes for checking for a clique of bigrams: let K and Q be sets of features such that B=K×Q. Then, we can check for the entire clique using the pure tensor (∑j∈K→fj)⊗(∑i∈Q→fi). Checking for this clique of feature bigrams on key-query pairs which don't contain any bigram in the clique contributes an interference term of √|K||Q|/dresid assuming interferences are uncorrelated. Now we require that the sum over interferences for checking all cliques of bigrams - of which there are at most dhead - is less than one. Since there are at most dhead cliques, then assuming each clique is the same size (slightly more generally, one can also make the cliques differently-sized as long as the total number of edges in their union is at most dresid) and assuming the noise is independent between cliques, we require √|K||Q|/dresid<1/√dhead. Further assuming |K|=|Q|, this gives that at most |K|=|Q|=dresid/√dhead. In this way, over all dhead cliques, we can check for up to d2resid bigrams, which can collectively involve up to dresid√dhead distinct features, in each attention head.
Note also that one can involve up to dheaddresid features if one chooses |K|=1 and |Q|=dresid (or the other way around) for each clique. In that case, noise from situations where the small side f-vector gets hit dominates — this is what forces the large side to have size at most dresid.
(Note how all these numbers compare to the parameter count of dresiddhead.)
3.4 Checking for a smaller unstructured set of feature pairs in superposition
We now consider the case that we would like to check for an arbitrary set of feature pairs. This is analogous to the task of computing a subset of ANDs of inputs in superposition. In this general case, we can’t assume that they form large cliques.
The construction is a generalization of our non-superpositional construction: we take a sum of pure tensors, one for each pair in B, and then take a low rank approximation at the end. We will now work through the details to figure out just how much computation we can fit in before the noise overwhelms the signal.
To be precise, the construction is that we let ^WQK:=^WQK(B)=∑(i,j)∈B→fi⊗→fj with |B|>dhead. We’ll continue the assumption that {→fi} are random vectors. To ensure that the matrix is rank dhead we will need to project it down somehow: we pick dhead random gaussian vectors, and write a projection matrix R which projects to the subspace spanned by these random vectors. In fact we will choose R to be this projection matrix scaled up by an amount dresiddheadso that (R→fi)⋅→fi=1. Then we write WQK=^WQKR.[29]
We'll give a heuristic argument now that this construction works — in particular, that it lets one make a QK circuit which checks for a generic set of up to dresiddhead bigrams (up to log factors), without assuming any structure to those bigrams.
We'd like to understand the size of noise in our QK-circuit, i.e. to understand →nT1WQK→n2=→nT1^WR→n2=→nT1⎛⎝∑(i,j)∈B→fj⊗(R→fi)⎞⎠→n2=∑(i,j)∈B(→n1⋅→fj)(→f′i⋅→n2) in the case that →n1,→n2 are random unit vectors. Each term in the sum is of size 1√dresiddhead, so the total noise is √|B|dresiddhead.
To understand the size of noise in our QK-circuit, we can see what happens when the residual stream vectors are replaced with random unit vectors →n1,→n2∉{→fj}. This simulates what we'd pick up if the two token positions of interest each had a single feature active, neither of which were in our set of bigrams. In this case we have
→nT1WQK→n2=→nT1^WR→n2=→nT1⎛⎝∑(i,j)∈B→fi⊗(R→fj)⎞⎠→n2=∑(i,j)∈B(→n1⋅→fi)(→f′j⋅→n2)
→f′i is a vector with a typical size of √dresiddhead due to the rescaling of R. Therefore each term in the sum is typically of size 1√dresiddhead, so exploiting that each term in the sum is independent, the total noise is on the order of √|P|dresiddhead. Now, if the key and query vector have κK and κQ features active respectively, with none of these features in any of our bigrams, then the total noise is √κKκQ|P|dresiddhead.
We might wonder what the noise term is from pure tensors →fi⊗vecf′j where →fi is present in →as but →fj is not present in →at (or the other way around). In this case, the size of the noise term will be 1/√dhead or 1/√dresid, depending on whether the feature is present in the query or the key[30].
As for the size of the signal, (ie the size of →aTsWQK→at for residual stream vectors in positions s,t which contain a bigram in B), we have
→aTs^WQK→at=→fTi′^WR→fj′=→fTi′⎛⎝∑(i,j)∈B→fj⊗(R→fi)⎞⎠→fj′=∑(i,j)∈B(→fi′⋅→fi)(→f′j⋅→fj′)
where (→fi′,→fj′)∈B. Since we rescaled R, the term in the sum for i=i′,j=j′ is equal to 1. For other terms in the sum, we get interference terms on the same scale as the noise above.
This means that in order for the signal to be larger than the noise, i.e. for us to get readoffs that are always in 1±ϵ or ±ϵ, we require |B| to be no larger than ~Θ(dresiddhead), and that no one feature is present in more than ~Θ(dhead) of the skip feature-bigrams. Note that the former condition implies the latter if we are allowed to further assume that the set of pairs in B is generic: if the pairs are chosen at randomly, for m≫dresid, each f-vector will be chosen roughly dresiddhead/m≪dhead times.
3.5 Copy-checker heads and structure-exploiting algorithms
Sometimes (often?) it is possible to check for a much larger set of skip feature-bigrams than any of the above algorithms suggest. This is when a large number of features are related to each other by a linear map, which may happen when there is a simple relationship between some subset of features and another subset. For example, perhaps there are a large number of female name features like {Michelle Obama, Marie Curie, Angelina Jolie...} and another large number of features corresponding to their husbands {Barack Obama, Pierre Curie, Brad Pitt...}. Then, the NN may be incentivised to arrange these features in such a way that there is a linear map that takes all female name features to their husband's feature, because this will allow an attention head to attend from the woman to instances of her husband in the text.
To see how this works, let F=→f1,…,→fm be an almost orthogonal overbasis of f-vectors (which can be exponentially large), and let M be an arbitrary orthogonal d×d matrix such that for all i, M→fi is approximately equal to at most one f-vector, and almost orthogonal to all the others. Let Φ⊆F be the set of f-vectors which are mapped to another vector in F by M and let Ψ=MΦ={M→ϕi|→ϕi∈Φ}⊆F. One such setup can be achieved as follows: choose M to be a random orthogonal matrix, and let Φ be an almost orthogonal set of unit vectors of size m/2. Then, with high probability, F:=Φ∪Ψ=Φ∪MΦ is also almost-orthogonal. Now let B={(→fi,M→fi)|→fi∈Φ}.
Then, choosing WQK to be is a random rank dhead approximation of M (scaled up by dresiddhead) will allow us to check for every element of B at once: For any i, if feature ϕi is in the query, then it will be mapped to a random scaled dhead dimensional projection of ψi by WQK, and contribute 1 to the dot product. Noise terms will be of size 1/√dresid.
In the husband-wife case, Φ is the set of women and Ψ is the set of their husbands. Then, an attention head which chooses WQK to be a low rank approximation to M can check for exponentially many wife-husband bigrams by exploiting that each wife feature can be mapped to the husband feature by the same linear transformation (the same rotation if we insist that M is orthogonal). Of course, this working depends on the very nontrivial assumption that there is this linear relation — this is probably false for these particular pairs in real models; it’s just an illustration, though see this paper which observes a similar phenomenon for relations between sports players and their sports, and in several other examples.
A special case of this is if ϕi=ψi for all i. In this case, the set B corresponds to a family of bigrams like "if the query has feature i then the key should have feature i also", and the keys that get paid the most attention to are those that are composed of the most similar features as the query. That is, M is the identity, and the attention head is performing the function of a copy-checker head.
The K-composition version of an induction head does something similar: Use the OV circuit of a previous head to copy many features from one subspace to another. Then choose WQK to be WTOV of the previous head.
So, it is possible to understand many of the functions that attention heads are previously known to perform in the lange of skip feature-bigram checking, which is good news. On the other hand, if many of the most important things done by attention heads exploit this linear structure, then it may be counterproductive to think in terms of memorized skip feature-bigrams. Certainly the skip feature-bigram description for copy-checker heads is less simple than the traditional description.
We think it is plausible there are also interesting constructions that combine the unstructured and structure-exploiting algorithms. That is, we can probably take WQK to track some unstructured union of linearly related feature pairs. We leave investigating this to future work.
Generalization as a limit of memorization
So, in our picture, copy-checker heads are attention heads which exploit the linear structure of the activation space to check for many conditions of the form
at the same time. Ths is conceptually subtly different to the standard story for copy-checker heads, in which we think of them as asking the more general question
or even
Even though the two descriptions describe the same behavior, we think that ours offers a story of how these general purpose attention heads can be learned:
Consider a setup without residual stream superposition. If the loss on some batch would be lower by checking for 'if feature 16 is present in the query, then feature 16 is present in the key', then perhaps that 'identity' bigram gets learned. So, WQK is updated from being the zero matrix to a matrix with a 1 in the (16,16) position (when written in the feature basis on the left and right). In a sense, this is a form of memorisation: the general task of language modeling would benefit from a copy-checker head here, but the model only learned to copy a specific feature that it saw on a particular batch. Over subsequent training, more 1s are placed along the diagonal, until eventually dhead identity bigrams have been memorized. At this point, we notice that WQK has become the identity matrix (in a dhead dimensional subspace), which is exactly the matrix that the generalizing algorithm (a copy-checker head which can copy any query vector back) requires. In this setup, enough memorization precisely led to generalization!
This also works, and looks somewhat more magical, if we allow the residual stream to contain a sparse overbasis (feature vectors are assumed to be random unit vectors again). Now, each time a specific identity bigram is learned, we have ^WQK (the bilinear form before projection to a random dhead dimensional subspace) is replaced with ^WQK+→fi⊗→fi for some particular i. After m bigrams have been learned, we have (after rescaling)
(^WQK)kl=dresidmm∑i=1(fi)k(fi)l→{1,k=l1/√m,k≠l
This approaches the identity as m grows (this can be made precise with the usual Chernoff and union bounds), such that the projection WQK approaches the low rank identity required for the generalizing copy-checker head.
4 QK: discussion
We have a few thoughts about how well this description captures the role of the QK circuit.
Where does softmax fit in?
If features are present in inputs with probability (sparsity) s, then skip feature-bigrams should generically be satisfied with probability s2 (assuming independence). For sparse enough inputs, it is very unlikely for more than one pair skip feature-bigram to be present on any pair of positions. In this case, entries in the attention score are almost always in {0,1} and the QK circuit can be thought of as computing ⋁(i,j)∈B(is fi present in (→as)∧is fj present in (→at)). In this case, if we scale up the QK circuit so that entries in the attention score are in {0,100}, then the softmax will kill the zero entries, and each row of the attention pattern will have entries that were 100 replaced with 1/r where r is the number of nonzero entries in the row. This makes sense — it will correspond to taking an arithmetic mean of the value vectors in the r positions that contain the first element of a feature bigram (with the second element of the pair in the query position). If, for a particular query, there is only one key that has a feature bigram in B with it, then this key will be attended to entirely.
However, if the features are less sparse, our task isn’t to check whether one of a set of feature bigrams is present, but rather count the number of pairs which are present. This means that for a particular query, if we scale up the QK circuit, then the attention pattern will be nonzero only on whichever key contains the most feature bigrams with the query (or on whichever set of keys ties for first place). We aren't sure if this is a feature or a bug.
Unknown unknowns
Attention layers are hard to interpret, not least because softmax is a beast. While it is known that attention patterns are good at looking back through the sequence for information and moving it around, it is not known if that is _all_ that they do (of course this limitation is not specific to our work). We make no predictions about whether future researchers will find entirely different things that the QK circuit can do that looks nothing like checking for skip feature-bigrams.
Does our QK construction really demonstrate superposition?
Just as it was possible to tell a story of the U-AND construction that didn't leverage superposition, it is possible to describe the construction of section 3.4 without mentioning superposition. In particular, the natural non-superpositional story would be to describe the matrix WQK=∑(i,j)∈B→fi⊗(R→fj) through its SVD:
WQK=dhead∑i=1σi→ui⊗→vi
We know that the sum only ranges over i=1,…,dhead because WQK has rank at most dhead. So we can interpret the QK circuit as calculating precisely dhead different projections on the right and on the left, multiplying the pairs and adding them, at each query and key token position.
The problem with this story is that each projection (each term like →vi⋅→at) doesn't have a nice interpretation in terms of our boolean features: it is some linear combination of the features with no short description length in terms of boolean variables. In general, the right and left singular bases of WQK have little to do with the residual stream overbasis, and if our goal is interpretability, we'd really like to understand WQK in the left and right feature overbasis, which is what we have done in this post.
4 How relevant are our results to real models?
The bounds we give in this paper are asymptotic and tend to have bad constant (or logarithmic) terms that are likely quite suboptimal. In some back-of-the-envelope calculations and experiments we did, they give high interference terms for modest model widths (on the order of hundreds of neurons). However, we believe that real networks might learn algorithms of a similar type that have much better constants, and thus implement efficient computation for realistic values. We hope that our asymptotic results capture qualitative information about what processes can be learned effectively in real-world models, rather than that our bespoke mathematical algorithms are the best possible.
More generally, we think that boolean computation can explain only a piece of the computational structure of the interpretation of a neural net. Some examples that are likely to be boolean-interpretable are bigram-finding circuits and induction heads. However, it's possible that most computations are continuous rather than boolean[31]. Second, many computations that occur in neural nets may not be best understood as boolean-style circuits, because the bits have important mathematical structure. In this case, the best interpretation may reference a range of mathematical components instead, like the complex multiplication map in modular addition. Nevertheless, we think that understanding boolean circuits is important, and we hope to come up with analogous results for continuous variables in the future.
So, the degree to which the picture we paint captures the computation happening in real transformer models is not clear to us. There are a range of options here.
We note that if circuits like the ones we describe do turn out to be present and useful in real transformers, there are two ways in which we expect the picture to be made more sophisticated. First, it has been observed that many computations that can be done in a single layer in a transformer are instead spread out (perhaps via random optimisation processes) to be gradually done over many layers. Second, there is evidence that there is important additional structure to the arrangement of the feature vectors. We think it would be interesting and natural to try to combine such additional structure with our picture of computation in superposition, and produce a more expressive (and, hopefully, more complete) theory of computation. We gesture at the beginnings of such a picture at the bottom of the section on the QK circuit, but a more complete picture of this type is outside our scope.
5 Open directions / what we're thinking about now
These are very rough bullet point lists. The items in each list are in no particular order, and the ordering of lists is not particular, either. Please get in touch with us if you are interested in pursuing any of these ideas, or if you want to talk through other theory/experiment ideas that aren’t on the list. If no one does so, we might publish a more fleshed-out set of ideas for future work.
The OV circuit
This story is preliminary and hasn’t been worked out in detail at the time of writing. One issue is that often attention heads do not attend to a single previous token position, but rather a mixture of several previous positions. Combining many value vectors in linear combination could break sparsity, and could also result in features being non-binary. We'd like to work on this story more in future.
Specifying concrete use cases
Genericity questions
We hope to run a series of experiments to check whether universal calculation is executed by random MLP’s (see the section “Is universal calculation generic” in the FAQ above). Specifically, we plan to train a readoff vector starting with a randomly initialized MLP to see whether it can accurately learn to read the output of suitable circuits.
Reverse-engineering
Understanding errors
Clarifying the model of computation
Potential reframings
How applicable are our setups to the real world?
Acknowledgments
We'd like to thank Nix Goldowsky-Dill, Simon Skade, Lucius Bushnaq, Nina Rimsky, Rio Popper, Walter Laurito, Hoagy Cunningham, Euan Ong, Aryan Bhatt, Hugo Eberhard, Andis Draguns, Bilal Chughtai, Sam Eisenstat, Kirke Joamets, Jonathon Liu, Clem von Stengel, Callum McDougall, Lee Sharkey, Dan Braun, Aaron Scher, Stefan Heimersheim, Joe Benton, Robert Cooper, Asher Parker-Sartori, and probably a bunch of other people we're unfairly forgetting now, for discussions and comments.
Attributions
In general, much happened in discussions, and many ideas of a member of the trio were built on top of previous ideas by another member. The following is a loose approximation, with many subtle and less subtle contributions omitted to keep it manageable.
The three authors would like to gratefully acknowledge Nix Goldowsky-Dill, who wrote an early version of the summary and helped with distillation (but declined to be named a coauthor). Jake and Kaarel posed the U-AND problem, providing the notions of representation involved. Dmitry came up with the first construction solving the U-AND tasks, as well as with the quadratic U-AND. Kaarel came up with the targeted superpositional AND. Jake led the write-up and editing efforts, with technical content largely based on informal notes by Kaarel; he also produced our finalized introductory sections based on Nix’s summary. The discussion and experiments comparing ϵ-accuracy to loss functions are Jake’s.
Kaarel came up with the initial structured and unstructured QK circuit constructions. The structure-exploiting variant came out of a discussion between Dmitry and Kaarel, and the associated story about memorization and generalization had contributions from Dmitry, Jake, and Kaarel. Jake clarified and simplified these ideas considerably, and wrote most of the QK section. OV is from Kaarel. Dmitry and Jake came up with Universal Keys; Dmitry wrote that section. The three all contributed significantly to the section on open directions. The appendix is Kaarel's, with some contributions by Dmitry and Jake.
Jake is a Research Scientist and Kaarel is a contractor at Apollo Research, and we would like to thank them for supporting this effort. Kaarel is a Research Scientist at Cadenza Labs. Dmitry is a post-doc at IHES.
Appendix: a note on linear readoffs, linear combinations, and almost orthogonality
This appendix is largely independent from the rest of the paper, other than that it explains a distinction between almost orthogonal overbases and the more general concept, which we will define, of linearly ϵ-readable overbases, which is what we think might be what is actually learned by neural nets (and which has the same good behavior from the point of view of a neural net and linear readability). We plan to post a version of this as a separate post, as we think it is a useful distinction and a plausible source of confusion. For the point of view of the (synthetic) algorithms of the present paper, either of these concepts can be used for our basis of f-vectors (modulo some issues with controlling errors).
Here we discuss this idea and a failed attempt to find additional structure (similar to ϵ-orthogonality) in linearly readable overbases. We then briefly discuss the possibility of linearly reading off features in the presence of linear relations between f-vectors, as well as a bound on the number of features that can be linearly read off in this setup.
The structure of activation vectors
Here's the setup. We have a data set X={x1,…,xD} of inputs to a model that then produces a respective data set A={a1,…,aD}⊆Rd of activation vectors, with ai=a(xi)[To be clear: we are letting a be the function that is implemented in the model to compute the activation vector in a particular activation space.]. For example, each xi might be a particular sentence, the model might be GPT-2, and the corresponding ai might be the residual stream activation vector at the last token position just after the fourth MLP. There are m functions f1,…,fm:X→{0,1} — we will think of these as the features (i.e., properties) of inputs which are represented in this particular activation space. We assume that we are in the superpositional regime: m≫d, but for each x∈X, the set of features which are on is small — in fact, that for each x∈X, there are at most ℓ≪d indices i∈[m] with fi(x)=1[35]. In fact, we assume that activation vectors are defined in terms of these properties in a particular linear way: that there are vectors →f1,…,→fm∈Rd — we call these the f-vectors corresponding to the properties — such that a(x)≈∑mi=1fi(x)→fi. Actually, let's make this a precise equality just to make our job a bit easier; we assume that each activation vector is a=→fi1+→fi2+⋯+→fiℓ′ for some ℓ′<ℓ and indices i1,i2,…,iℓ′. We'll think of the compositeness ℓ as a constant and d as large (and m larger still). In fact, we'll primarily consider what happens asymptotically in d. For a concrete example, one can take= ℓ=10, d=1000, m=100000, for example.
Linear readability and its consequences
To be able to directly compute other properties out our basic feature vectors, it would be good for each of these properties to be linearly readable, by which we mean that for each i, there's a vector →ri∈Rd[36] such that →rTi→a(x)≈fi(x) for all x. Let's say this again:
> Definition. Let X be a set of inputs, let →a:X→Rn give the corresponding activation vectors (in a particular position/layer in a given model). We say that f1,…,fm are linearly readable up to error ϵ from these activation vectors if there are vectors →r1,…,→rm∈Rd such that for all i∈[m] and x∈X, we have |→rTi→a(x)−fi(x)|≤ϵ[37].
Let's think about what kinds of f-vector families →f1,…,→fm would give rise to activation vectors from which f1,…,fm are linearly readable up to error ϵ. Let's first note that if |→rTi→fj−δij|≤ϵ — let's call this the f-vectors →f1,…,→fm being linearly readable up to error ϵ — then f1,…,fm are linearly readable up to error kϵ[38]. Conversely, at least assuming the data set is rich enough to have a minimal pair for each feature fi, i.e. a pair of inputs x1,x2∈X such that fi′(x2)−fi′(x1)=δii′ (think of this as a condition that the features should be sort of independent of each other — in particular, if there's a feature whose value is uniquely determined by the values of other features, this would be false), the features being linearly readable up to error ϵ from activation vectors implies that the f-vectors →f1,…,→fm are linearly readable up to error 2ϵ, too. So, at least for constant k, features being linearly readable from activations is roughly the same as the underlying f-vectors being linearly readable. A precise statement we could make here is that if we fix some function g(d), then a sequence as d→∞ of such setups having features be linearly readable up to error O(g) from activations is equivalent to the sequence of corresponding f-vector sets being linearly readable up to error O(g). So, while it is perhaps prima facie better-justified to ask for features being linearly readable up to error ϵ from activation vectors, it's (more or less) equivalent to ask for f-vectors being linearly readable up to error ϵ, and this is mathematically nicer, so let's proceed to think about that instead. If you are worried about this switch not being entirely rigorous, don't be: the only thing we really logically need for what we're about to say is that f-vectors being linearly readable up to error ϵ implies that features are linearly readable from activations up to error O(ϵ). The reason this is sufficient for our express purpose of understanding whether linear readability of features implies that the f-vectors have some other interesting structure (perhaps structure that could help us identify f-vectors in practice[39]) is that this implies that constructing a set of f-vectors →f1,…,→fm which are linearly readable up to error ϵ/k but that do not have some certain property also gives a construction where the corresponding features are linearly readable up to error ϵ from activation vectors but the underlying →f1,…,→fm do not have that property — just take the data set of activation vectors to consist of all sums of up to k of the →f1,…,→fm.
Let's think about what kinds of collections →f1,…,→fm are linearly readable up to error ϵ. A choice of →ri that might immediately suggest itself is →ri=→fi; the features being linearly readable up to error ϵ with these →ri is just the condition that the →fi have squared norm within ϵ of 1 and are pairwise almost orthogonal: more precisely, with ⋅ denoting the standard inner product, for all i≠j, we have |fi⋅fj|≤ϵ. Supposing the f-vectors have (about) unit norm, is something like being almost orthogonal also necessary given some reasonable assumptions? Well, we could have the f-vectors be almost orthogonal w.r.t. the standard inner product in some other basis, and we could then clearly linearly read stuff after writing the vectors in this basis, but we could also compose the basis change and the readoff into just a linear readoff, so being almost orthogonal in any basis suffices for →f1,…,→fm to be linearly readable. And being almost orthogonal in some other basis doesn't imply being almost orthogonal in the usual basis; e.g., consider the case where all the basis vectors are almost equal in the usual basis. Is being almost orthogonal in some basis required though? Also no! Let →f1,…,→fm∈Rd be sampled in bundles: by taking m/ℓ=ed0.99 independent uniformly random unit vectors →g1,…,→gm/ℓ∈Rd and then generating a batch of ℓ=en0.99 f-vectors →fj from each →gi (namely, those with j=ℓi+1,…,ℓ(i+1)) by adding another independent uniformly random vector →vij of length (let's say) 1logn to it: →fj=→gi+→vij. One can (with very high probability) read off every resulting →fj just fine using →rj=logn⋅→vij up to error ϵ=o(1). But with very high probability, there's no basis in which these →fj are almost orthogonal almost unit vectors up to error ϵ′=1/10 — see the appendix to this appendix for a sketch of a proof.
Let's finish this section by mentioning a few variations on the above. What if we require readoff vectors to have norm bounded by a constant? (For instance, maybe (explicit or implicit) weight regularization would make this requirement reasonable.) The construction above but with →vij of length 1/100, scaled back down by $\sqrt{\frac{10000}{10001}}$, still provides a counterexample. (If we require →ri to have norm very close to 1, then we're forced to pick →ri≈→fi, and then →fi indeed have to be almost orthogonal according to the canonical inner product, but that's sort of silly.) What if we replace the requirement that features are almost unit vectors in the new basis with the weaker one that the features have norm between some two particular nonzero constants? One can still use the proof in the appendix-appendix to show that there's no such basis. What if we get rid of any norm requirement (other than that the vectors are nonzero — but this is implied by a change of basis anyway), just requiring almost orthogonality in the sense that for any j≠j′, we have →fj⋅→f′j≤ϵ||→fj||||→f′j|| in the new basis? Note that this is actually a less natural requirement in our context than it might first seem — this is because it doesn't imply that the properties are linearly readable. But anyway, (1) we're quite certain that the above is still a counterexample, (2) we haven't thought very much about how to adapt the proof in the appendix-appendix to show it is, (3) the rest of the argument would work as in the appendix-appendix if one could show that it's unlikely there's a B−1 with σ1/σn>n100.
Linear readability and linear relations
If the values of features f1,…,fm vary independently, then any linear relation between their feature vectors with coefficients that are not too uneven will render reading them off from activations impossible. More precisely, suppose that →fi=∑jaj→fj. Then if there were a corresponding readoff vector →rTi, we'd have →rTi→fi=∑jaj→rTi→fj, so 1=O(ϵ(1+∑jaj)). Unless ∑jaj=Ω(1/ϵ) — the sum of coefficients is big — we have a contradiction. If we put a bound on the norm of →ri and the norms of →fj, then an approximate linear relation fi≈∑jaj→fj also provides a similar contradiction. Similarly, a linear relation on →rj=∑jaj→rj with small coefficients (or an approximate version, given bounds on the vectors ||→ri|| and ||→fi|| also yields a contradiction.
However, if the values of properties do not vary independently, then linear relations between readoffs are totally fine. For example, if we have atomic properties f1:X→{0,1}, f2:X→{0,1}, and the following two properties derived from them: f3=f1∧f2 and f4=f1∨f2, and the activation vector in the standard basis is →a(x)=(f1(x),f2(x),f1(x)∧f2(x)), then we can read off the four properties with 0 error with →r1=(1,0,0),→r2=(0,1,0),→r3=(0,0,1),→r4=(1,1,−1) even though there is a linear relation between these readoff vectors, because there is a corresponding linear relation between the properties. Though there's some arbitrary-feeling choice here, and in fact the choice we make is perhaps not the most natural, we may also see it as a linear combination of 4 corresponding features between which there is a linear relation — we may expand (f1(x),f2(x),f1(x)∧f2(x))=f1(x)(2,1,0)+f2(x)(1,2,0)+f3(x)(−1,−1,1)+f4(x)(−1,−1,0). This merits more thought.
A bound on the number of linearly readable features
A simple restatement of the features being linearly ϵ-readable is that, letting F denote the m×n matrix whose rows are →f1,…,→fm, there's an n×m matrix R such that FR has L∞ distance at most ϵ from the identity matrix. Given this translation, Theorem 1.1 here tells us that if →f1,…,→fm∈Rd are linearly readable up to error ϵ, then m≤eCϵ2log(1ϵ)d. Or see here for a neat proof of the same upper bound in the subcase where we force →ri=→fi. And both bounds are tight up to the log(1/ϵ) factor in the exponent since a set of eCϵ2d random unit vectors is almost orthogonal with high probability — this provides some very weak sense in which linear readability doesn't give more flexibility than almost-orthogonality.
Appendix to the appendix
Here's a sketch of a proof that there is no basis in which construction provided above is almost-orthogonal (if you have a neater proof, let us know). We’re dropping arrows on vectors here. (Here, fi always denotes the vector.)
Let us consider what needs to be the case if there is a basis which makes the fj almost unit and almost orthogonal with parameter ϵ′. Let a linear map that takes a vector to its representation in such a basis be B−1. We have maxv∈Sn−1||B−1v||=σ1, the top singular value of B−1, in fact with B−1v1=σ1u1 in terms of the top respectively right and left singular vectors of B−1. Up to replacing ϵ′←2ϵ′, we can always assume that the smallest singular value σn is at least ϵ′/100 — this is because one can replace B−1 with a matrix with the same SVD but with singular values shifted up by ϵ′/100 — one can check that this does not affect dot products by more than ϵ′. Additionally, note that the max of the three numbers ||B−1gi||||gi|| and ||B−1vij||||vij|| and ||B−1vij′||||vij′|| (for some j≠j′) was ever within a factor of √logn of the min of these three numbers, then B−1fj having almost unit norm would imply that B−1gi also has almost unit norm, and then one could derive a contradiction from the requirement that (B−1fj)⋅(B−1fj′)=O(ϵ′). It follows that be that for any i, ||B−1gi||||gi|| is at least √logn times larger than ||B−1vij||||vij|| for all but at most one index j from its bundle. For this index, we still have that ||B−1gi||||gi||≥||B−1vij||||vij||σnσ1 It then follows that
||B−1gi||||gi||≥(σnσ1(logn)en0.99/2−1)1/en0.99(∏j||B−1vij||||vij||)1/en0.99
Intuitively, this is saying that B−1 applies a systematically larger scaling to vij than to gi.
However, one can use a pair of arguments using nets that with high probability, there is no matrix B−1 satisfying all these properties.
First, with high probability, there is no such matrix with σ1≥n. This is because we can show that with high probability, for every such matrix, there is some fj with ||B−1fj||≥2. Indeed, one can show that with high probability, for every unit vector v at once, there is some fj=fj(v) so that fj⋅v≥1√n; in particular, such a fj thus exists for the top right singular vector v1, and then expanding fj in the basis of right singular vectors easily gives ||B−1fj||=Ω(√n).
A sketch of a proof that with high probability, for every vector on the sphere at once, there is an fj which is near it in this sense: before we sample the fj, we pick an appropriate net — for us, this will be a set on the sphere such that for each point on the sphere, some point on the net is closer than (let's say) ε=1n to it. To construct such a net, keep adding points on the sphere arbitrarily, making sure that each point added has distance at least ε to all previously added points, until we get stuck. In fact, we must get stuck after at most (2ϵ/2)n=(4n)n≤O(e2nlogn) points because balls of radius ε2 around added points must be disjoint and contained in a ball around the origin of radius 2. When we get stuck, every point on the sphere has distance at most ε=1n to some chosen point, so we have a desired net with O(e2nlogn) points. For a point in this net, the probability that no fj has dot product at least 2√n with it is at most c−en0.99 for some c<1. As the size of the net is only singly exponential, so we can easily union-bound over the net to say that with high probability, for every point of the net, there is some corresponding fj with dot product at least 2√n with that point of the net. If that happens, for any point u on the sphere, we get that there is a fj with dot product at least 1√n with it as well, because there's a point of the net closer to u than 1n, let's call this point s, and there is a fj with s⋅fj≥2√n, so u⋅fj=s⋅fj+(u−s)⋅fj≥2√n−1n≥1√n
Secondly, with high probability, there is also no such matrix B−1 with σ1≤n. In this case, we use a Frobenius norm ϵ′/10000 net in the set of all matrices with σ1≤n and σn≥ϵ′/100. Since the entries of any such matrix are bounded by some polynomial in n, a similar volume argument as the one in the previous paragraph applied to balls in a cube in Rn2 shows that there exists such a net of size exp(poly(n)). Since the Frobenius norm is an upper bound of the operator norm, this net also serves as an ϵ′/10000 net w.r.t. the operator norm. This guarantees that for every such matrix M and any nonzero vector v∈Rn, there is a net element N with ||Mv||||v|| differing from ||Nv||||v|| by at most 1%. We now consider log⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝(∏i||Ngi||||gi||)1/en0.99(∏i∏j||Nvij||||vij||)1/e2n0.99⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠=∑ilog(||Ngi||||gi||)en0.99−∑ijlog(||Nvij||||vij||)e2n0.99 Each of these summands is between logϵ′/100=log1/500 and logn, so we can apply https://en.wikipedia.org/wiki/Hoeffding%27s_inequality to conclude that the probability of a deviation of log((logn)1/3) from the expected value of 0 is less than e−en0.99/(100log2n). So this never happens for any matrix N in the net by a union bound over the merely exp(poly(n)) matrices in the net. Since any matrix with σ1≤n and σn≥ϵ′/100 has a matrix N in the net for which their respective expressions differ by at most 0.01, it follows that there's no such matrix B−1 with σ1≤n with
∏i||B−1gi||||gi||≥∏i⎛⎜ ⎜⎝(σnσ1(logn)en0.99/2−1)1/en0.99(∏j||B−1vij||||vij||)1/en0.99⎞⎟ ⎟⎠
Since there being a basis in which this set of vectors is almost orthogonal implies that one of the two things we've considered above happens, and each happens with probability o(1), one of them happening also has probability o(1). So w.h.p., neither happens — and so w.h.p., there's no basis in which this set of vectors is almost orthogonal.
Kaarel and Jake would also be interested in distributing microgrants to such people if someone would like to fund this please get in touch
Up to a log factor in the number of neurons
In practice for the specific case of wheels and doors, the sum of these features would work similarly well. However, this is just an illustrative example of a boolean function. As we discuss in the body of the text, being able to compute any boolean function is much more expressive than only computing linear functions. Perhaps a better example specific to a transformer is the feature "will_smith" = "will@previous_token" AND "smith@this_token".
In the sense of taking only a small number of inputs
These are called feature representation vectors, feature embedding vectors, and feature directions in Toy Models of Superposition, and feature embedding vectors in Polysemanticity and Capacity. We like the term feature vectors but this is used already to mean the input vector which stores features.
The precise formula is that for some constant C, up to exp(Cϵ2d) random vectors will be ϵ-almost-orthogonal with probability approaching 1.
Really, ϵ and ℓ could be functions of other parameters, but let’s ignore that.
In fact, we will abuse notation a bit in this paragraph by using x to denote both a binary string and its input embedding, only distinguishing them with the use of an overarrow.
Although there are some subtleties here, and it's not obvious that small p always improves the worst-case interference, even though it does minimise the expected interference.
One might be able to get a better bound here, perhaps by using something sharper than a Chernoff bound, more appropriate for far tails of the binomial distribution with very small p — we haven’t thought carefully about optimizing this error term.
assuming that one allows a fixed input of 1, which one can implement as an offset
See section 1.2 for a way to efficiently compute ANDs of multiple inputs in a single layer, which may dramatically improve the efficiency of the computation of suitable circuits]
Maybe it’s fine if some neurons misfire as long as the total signal on the |Si∩Sj| neurons in a pairwise intersection beats the total noise? We think maybe this lets one do up to about rd0 inputs per neuron, and one might get up to about m=√rd0√d≤d3/20√d input features this way. So this might get one a little further.
While this appears worse than U-AND in the regime in which U-AND works, it is actually not because the construction below also solves the U-AND task in that regime. There might be a way to interpolate between U-AND and this construction — we speculate on this in the open directions.
To see this, for example note that monomial decomposition in boolean algebra implies that any circuit can be written as a large XOR of multi-input ANDs; now a multi-input XOR can be written as a linear combination of AND circuits using a modified inclusion-exclusion. For a more geometrical picture, consider that a boolean circuit can be thought of as a complicated Venn Diagram with k overlapping regions, with a 1 or a 0 assigned to each of the 2k regions including the outside. To recreate a particular boolean function out of ANDs, start by choosing the fan-in-0 AND (a constant) to have a coefficient equal to the value of the function outside all circles. Then add in each fan-in-1 AND (just the variables) with coefficients that ensure that all the regions in just 1 circle have the correct value. Then add in the fan-in-2 ANDs with coefficients that fix the function value on pairwise intersections. Then fan-in-3 for the triple intersections, and so on, with the coefficients of the 2k ANDs of fan-in up to k each being constrained by exactly one region of the diagram
We haven’t carefully thought about which method is better in some more meaningful sense though. Both of these constructions work for choices of k up to around polylog(d0), at which point the noise starts to become an issue.
The factor 12ℓ can be replaced by any value <1ℓ
Suppose that wμ,ν is a vector on Rr2 such that the dot product wμ,ν⋅Q(v)=qμ,ν(v), for qμ,ν(v)=(v⋅eμ)(v⋅eν) the quadratic function. Note that we can choose wμ,ν=wν,μ. Then the linear readoff function Φi,j is given by taking dot product with the readoff vector wi,j:=12∑(vi⋅eμ)(vj⋅eν)wμν.
By distributivity, this expression has s2 terms of the form ϕi,j(vi′,vj′), all of which except possibly ϕi,j(vi,vj)=1 are bounded by 2ϵ, giving the result. But in fact, one can get a better bound by noting that |ϕi,j(vi′,vj′)|<ϵ when (i,j) and (i′,j′) do not share an index.
In fact, O((m+ee)) is sufficient
Note that the efficiency gain from universal keys is bounded by the size of the context window: for example, one can convert a transformer to an MLP at the cost of making the layers much wider, thus neutralizing the information asymmetry. However, in the asymptotic where the size of the context window goes to infinity, these methods do seem to asymptotically improve the expressivity of boolean circuits one can execute in a superpolynomial way compared to previously known methods
This paper provides a more careful analysis of the same topic. V-information might also be relevant. But we’ve only skimmed each paper.
Or we can see it as precisely computing a family of functions which record the number inputs in a particular subset are present on the input, minus one.
Of course, there is really structure in this family of subsets — they come from intersections of larger subsets, meaning they can be specified more succinctly than this — the point we are making is precisely that it is natural to forget that structure in the superposition picture.
Note that if we insist that the output is normalised, then the maximum L2 distance of a unit vector from our target 1-hot vector, with individual entries differing by at most epsilon, is of order epsilon. In this case the two notions of successful reconstruction are aligned. One might think that the presence of layernorm in real models precisely normalises vectors in this way, but this is neglecting to remember that our target (1,0,0,…) is only tacked onto the end of the architecture to demonstrate that all the AND features are linearly represented immediately after the ReLU. The part of our toy model that corresponds to the part of a neural network with layernorm would be the activation vector immediately after the ReLUs, which contains a sparse feature basis. Layernorm applied to this vector would not do much, and would not correspond to the final large vector being normalised.
Related.
Much like it’s not a very novel idea that a ReLU layer might compute boolean functions of features, we do not claim that the idea that the QK part of an attention head could check for one of some set of pairs of features is very novel, though we don’t know of this task having been made precise in the way we do before.
Nevertheless, we think that morally, the first notion is what’s needed — that there could be a version of this section which only uses a slightly stricter version of the first notion.
This method is slightly unsatisfactory because it doesn't treat the row space and the column space equivalently. This can be solved by writing ^WQK as a sum of pure tensors using the SVD and including only the dhead pure tensors with the highest singular values, which also has the advantage of being the best approximation to ^WQK (in the sense of Frobenius norm distance or operator norm distance), and therefore which will give us the best signal to noise ratio. The reason why we don't do this here is because it is hard to reason about the distribution of singular values, and it doesn’t seem trivial to argue that the singular vectors are ‘independent’ of the f-vectors. We think that the details do work out even though we can't prove it and that in practice, the optimal algorithm involves taking this best low-rank approximation of ^WQK instead of a random one. However, we expect that this only improves the signal to noise ratio (and hence the number of bigrams we can check for) by a constant factor, because all the singular values of a random gaussian matrix live at the same scale (see here). In more detail:
We take its SVD ^WQK=∑dresidj=1σj→uj→vTj, and we let the bilinear form be the best rank dhead approximation of ^WQK, i.e., WQK=∑dheadj=1σj→uj→vTj.
Entries of ^W are a sum over |P| products of two i.i.d. gaussian random variables. We don't know how to say this rigorously (although we think this is the kind of thing which is easy to check experimentally), but we think that in the relevant range of |P| (maybe let's say |P|=dresiddhead/log2dresid), the matrix ^W is pretty much distributed as a random matrix with i.i.d. gaussian entries. We're probably not in the range where this becomes a trivial consequence of the multivariate CLT, because |B|, the number of terms, will not be big compared to d2resid, the number of entries. The singular values of gaussian matrices are understood well (e.g. see the article on the Pastur Distribution); the basic thing we'll assume now (that we're 98% sure is true) is that basically all the singular values of such a matrix live at the same scale, i.e. there is a size s (that depends on |B| and dresid) such that all but the smallest 1% of singular values are between s/1000 and s.
If we assume this, it becomes easy to understand the size of noise in our QK-circuit, i.e. to understand →nT1WQK→n2=→nT1(∑dheadj=1σj→uj→vTj)→n2 in the case that →n1,→n2 are random unit vectors. This is a linear combination of a bunch of things (i.e., σj) of size roughly s with coefficients (i.e., (→n1⋅→uj)⋅(→vj⋅→n2)) which are roughly independent and have distributions which are symmetric around 0 and which have size roughly 1/dresid. In particular, it has size on the order of s√dheaddresid.
To find s: Since the noise term →nT1^WQK→n2=→nT1(∑dresidj=1σj→uj→vTj)→n2=→nT1(∑(i,j)∈P→fj⊗→fi)→n2 has size on the order of s√dresiddresid but also on the order of √|P|dresid, we have that s is about √|P|√dresid, and the noise is of order √dhead|P|d3resid. (There are also other ways to compute the scale of s or the scale of the noise.)
As for the size of the signal: as in the main text we have →aTt^WQK→as≈1. Assuming this signal 'distributes nicely over the SVD' (sketchiest step by far, but probably right for m≫dresid and another thing which would be easy to check with an experiment), i.e. given 1≈→aTsWQK→at=∑dresidj=1σj→aTs→uj→vTj→at, we can conclude →aTsWQK→at≈∑dheadj=1σj∑dresidj=1σj; this is on the order of dheaddresid given the fixed scale assumption from the previous paragraph. Also importantly, it is dheaddresid times some constant independent of the pair (that can be computed by integrating the Pastur Distribution) — this means that the improvement the SVD gives over a random projection is only a constant amount. (We also wrote a bit of code before we understood how to figure this SVD thing out conceptually — it seems to work empirically as well.)]
Again, this asymmetry would not be present if we used the SVD instead.
Though this can be salvaged, e.g. with the language of arithmetic circuits from Appendix D.1 in Christiano et al.
Again, using a low-rank approximation given by the SVD is more natural, though again, it doesn’t look like it gives an improvement of more than a constant factor here.
More generally, we want our interpretability techniques not to fail silently, and to tell us how they are failing. We expect that if someone is able to get a good example of a task which involves computation that is truly in superposition throughout, this will be a good testbed for studying which interpretability techniques can be misleading. Can SAEs recover the correct AND features? Do analyses based on the neuron basis or SVD lead to spurious results?
For example, if layer L has f(L) pairwise AND nodes, (except for the first layer, which has input nodes) then if l nodes are on in layer L, (assuming the inputs to each AND are chosen independently uniformly at random) the expected number of nodes which are on in layer L+1 is f(L+1)⋅lf(L)l−1f(L). So we’d get steady-state behavior of the number of nodes which are on in expectation (this is a priori distinct from some actual convergence guarantee though; we’re just making it a martingale) iff f(L+1)⋅kf(L)k−1f(L)=k, so f(L+1)=f(L)2k−1
Assuming each feature is on roughly equally often, a double counting argument says that this is roughly the same as each feature only being active on at most about a particularly small fraction of all inputs: |p−1j(1)|D≈ℓm≪dm.
Well, more precisely, you should maybe think of this Rd as the dual space of the activation space Rd, i.e., of each →ri as a linear function on activation space, →ri:Rd→R.
We could also weaken this so that maybe we're fine with some very small number of errors — of probe outputs outside this range. The story to follow a fortiori also holds with this weaker definition.
This is a worst-case bound; in nice cases, the typical error should be more like √kϵ.
Well, being linearly readable up to error ϵ is already directly structure that might be helping us find f-vectors in practice — it seems plausible that this is related to sparse autoencoders with linearly computed coefficients making sense (compared to e.g. more canonical sparse coding methods) — though unclear if this can be squared with the ReLU in their hidden layer (or if that ReLU can be squared with this).