The typical noise on feature caused by 1 unit of activation from feature , for any pair of features , , is (derived from Johnson–Lindenstrauss lemma)
1. ... This is a worst case scenario. I have not calculated the typical case, but I expect it to be somewhat less, but still same order of magnitude
Perhaps I'm misunderstanding your claim here, but the "typical" (i.e. RMS) inner product between two independently random unit vectors in is . So I think the shouldn't be there, and the rest of your estimates are incorrect.
This means that we can have at most simultaneously active features
This conclusion gets changed to .
Good point. I need to think about this a bit more. Thanks
Just quickly writing up my though for now...
What I think is going on here is that Johnson–Lindenstrauss lemma gives a bound on how well you can do, so it's more like a worst case scenario. I.e. Johnson–Lindenstrauss lemma gives you the worst case error for the best possible feature embedding.
I've assumed that the typical noise would be same order of magnitude as the worst case, but now I think I was wrong about this for large .
I'll have to think about what is more important of worst case and typical case. When adding up noise one should probably use worst typical case. But when calculating how many features to fit in, one should probably use worst case.
I think it's pretty tricky, because what matters to real networks is the cost difference between storing features pseudo-linearly (in superposition), versus storing them nonlinearly (in one of the host of ways it takes multiple nn layers to decode), versus not storing them at all. Calculating such a cost function seems like it has details that depend on the particulars of the network and training process, making it a total pain to try to mathematize (but maybe amenable to making toy models).
I think it's reasonable to think about what can be stored in a way that can be read of in a linear way (by the next layer), since that are the features that can be directly used in the next layer.
storing them nonlinearly (in one of the host of ways it takes multiple nn layers to decode)
If it takes multiple nn layers to decode, then the nn need to unpack it before using it, and represent it as a linear readable feature later.
Thanks for writing this up, I found it useful to have some of the maths spelled out! In particular, I think that the equation constraining l, the number of simultaneously active features, is likely crucial for constraining the number of features in superposition
Neat, thanks. Later I might want to rederive the estimates using different assumptions - not only should the number of active features L be used in calculating average 'noise' level (basically treating it as an environment parameter rather than a design decision), but we might want another free parameter for how statistically dependent features are. If I really feel energetic I might try to treat the per-layer information loss all at once rather than bounding it above as the sum of information losses of individual features.
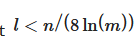
Calculating l, the maximal number of simultaneously active features, yields strange results. For example, if we have 100 features and 100 neurons, l has to be < 100/(8 * ln(100)) = 2.7. But I would expect that 100 features can be simultaneously active because we have 100 dimensions, so the features can be orthogonal and independent. Am I understanding something wrong?
The math in the post is super hand-wavey, so I don't expect the result to be exactly correct. However in your example, l up to 100 should be ok, since there is no super position. 2.7 is almost 2 orders of magnitude off, which is not great.
Looking into what is going on: I'm basing my results on the Johnson–Lindenstrauss lemma, which gives an upper bound on the interference. In the post I'm assuming that the actual interference is order of magnitude the same as the this upper bound. This assumption is clearly fails in your example since the interference between features is zero, and nothing is the same order of magnitude as zero.
I might try to do the math more carefully, unless someone else gets there first. No promises though.
I expect that my qualitative claims will still hold. This is based on more than the math, but math seemed easier to write down. I think it would be worth doing the math properly, both to confirm my claims, and it may be useful to have more more accurate quantitative formulas. I might do this if I got some spare time, but no promises.
my qualitative claims = my claims about what types of things the network is trading away when using super position
quantitative formulas = how much of these things are traded away for what amount of superposition.
I don't expect this post to contain anything novel. But from talking to others it seems like some of what I have to say in this post is not widely known, so it seemed worth writing.
In this post I'm defining superposition as: A representation with more features than neurons, achieved by encoding the features as almost orthogonal vectors in neuron space.
One reason to expect superposition in neural nets (NNs), is that for large n, Rn has many more than n almost orthogonal directions. On the surface, this seems obviously useful for the NN to exploit. However, superposition is not magic. You don't actually get to put in more information, the gain you get from having more feature directions has to be paid for some other way.
All the math in this post is very hand-wavey. I expect it to be approximately correct, to one order of magnitude, but not precisely correct.
Sparsity
One cost of superposition is feature activation sparsity. I.e, even though you get to have many possible features, you only get to have a few of those features simultaneously active.
(I think the restriction of sparsity is widely known, I mainly include this section because I'll need the sparsity math for the next section.)
In this section we'll assume that each feature of interest is a boolean, i.e. it's either turned on or off. We'll investigate how much we can weaken this assumption in the next section.
If you have m features represented by n neurons, with m>n, then you can't have all the features represented by orthogonal vectors. This means that an activation of one feature will cause some some noise in the activation of other features.
The typical noise on feature f1 caused by 1 unit of activation from feature f2, for any pair of features f1, f2, is (derived from Johnson–Lindenstrauss lemma)
ϵ=√8ln(m)n [1]
If l features are active then the typical noise level on any other feature will be approximately ϵ√l units. This is because the individual noise terms add up like a random walk. Or see here for an alternative explanation of where the root square comes from.
For the signal to be stronger than the noise we need ϵ√l<1, and preferably ϵ√l≪1.
This means that we can have at most l<n/(8ln(m)) simultaneously active features, and m<exp(n/8) possible features.
Boolean-ish
The other cost of superposition is that you lose expressive range for your activations, making them more like booleans than like floats.
In the previous section, we assumed boolean features, i.e. the feature is either on (1 unit of activation + noise) or off (0 units of activation + noise), where "one unit of activation" is some constant. Since the noise is proportional to the activation, it doesn't matter how large "one unit of activation" is, as long as it's consistent between features.
However, what if we want to allow for a range of activation values?
Let's say we have n neurons, m possible features, at most l simultaneous features, with at most a activation amplitude. Then we need to be able to deal with noise of the level
noise=aϵ√l=a√8lln(m)n
The number of activation levels the neural net can distinguish between is at most the max amplitude divided by the noise.
anoise=√n8lln(m)
Any more fine grained distinction will be overwhelmed by the noise.
As we get closer to maxing out l and m, the smaller the signal to noise ratio gets, meaning we can distinguish between fewer and fewer activation levels, making it more and more boolean-ish.
This does not necessarily mean the network encodes values in discrete steps. Feature encodings should probably still be seen as inhabiting a continuous range but with reduced range and precision (except in the limit of maximum super position, when all feature values are boolean). This is similar to how floats for most intents and purposes should be seen as continuous numbers, but with limited precision. Only here, the limited precision is due to noise instead of encoding precision.
My guess is that that the reason you can reduce the float precision of NNs with out suffering much inference loss [citation needed], is because noise levels and not encoding precision is the limiting factor.
Compounding noise
In a multi layer neural network, it's likely that the noise will grow for each layer, unless this is solved by some error correction mechanism. There is probably a way for NNs to deal with this, but I currently don't know what this mechanism would be, and how much of the NNs activation space and computation will have to be allocated to deal with this.
I think than figuring out this cost from having to do error correction, is very relevant for weather or not we should expect superposition to be common in neural networks.
In practice I still think Superposition is a win (probably)
In theory you get to use less bits of information in the superposition framework. The reason being that you only get to use a ball inside neuron activation space (or the interference gets to large) instead of the full hyper volume.
However, I still think superposition let's you store more information in most practical applications. A lot of information about the world is more boolean-ish than float-ish. A lot of information about your current situation will be sparse, i.e. most things that could be present are not present.
The big unknown is the issue of compounding noise. I don't know the answer to this, but I know others are working on it.
Acknowledgement
Thanks to Lucius Burshnaq, Steven Byrnes and Robert Cooper for helpful comments on the draft of this post.
In Johnson–Lindenstrauss lemma, ϵ is the error in the length of vectors, not the error in orthogonality, however for small ϵ, they should be similar.
Doing the math more carefully, we find that
|cosθ|≤(2+√2)ϵ+O(ϵ2)
where θ is the angle between two almost orthogonal features.
This is a worst case scenario. I have not calculated the typical case, but I expect it to be somewhat less, but still same order of magnitude, which is why I feel OK with using just ϵ for the typical error in this blogpost.