This could have been a relatively short note about why "zero sum" is a misnomer, but I decided to elaborate some consequences. This post benefited from discussion with Sam Eisenstat.
"Zero Sum" is a misnomer.
The term intuitively suggests that an interaction is transferring resources from one person to another. For example, theft is zero-sum in the sense that it cannot create resources only transfer them. Elections are zero-sum in the sense that they only transfer power. And so on.
But this is far from the technical meaning of the term.
In order for the standard rationality assumptions used in game theory to apply, the payouts of a game must be utilities, not resources such as money, power, or personal property. Zero-sum transfer of resources is often far from zero-sum in utility.
But I'm getting ahead of myself. Let's examine the technical meaning of "zero sum" more precisely.
It's used to mean "constant sum".
The term "zero sum" is often used as a technical term, referring to games where the payouts for different players always sums to the same thing.
For example, the game rock-paper-scissors is zero sum, because it always has one winner and one loser.
More generally, constant-sum means that if you add up the utility functions of the players, you get a perfectly flat function.
"Constant sum" doesn't really make sense as a category.
It makes sense to conflate "zero sum" and "constant sum" because utility functions are equivalent under additive and positive multiplicative transforms, so we can always transform a constant-sum game down to a zero-sum game. However, by that same token, the concept of "constant sum" is meaningless: we can multiply the utility of one side or the other, and still have the same game. If you have good reflexes, you should hear "zero sum"/"constant sum" and shout "Type error! Radiation leak! You can't sum utilities without providing extra assumptions!"
Let's look at the "zero sum" game matching pennies as an example. In this game, two players have to say "heads" or "tails" simultaneously. One player is trying to match the other, while the other player is trying to be different from the one. Here's one way of writing the payoff matrix (with Alice trying to match):
| Bob | |||
| Alice | Heads | Tails | |
| Heads | Alice: 1 Bob: 0 | Alice: 0 Bob: 1 | |
| Tails | Alice: 0 Bob: 1 | Alice: 1 Bob: 0 | |
In that case, the game has a constant sum of 1. We can re-scale it to have a constant sum of zero by subtracting 1/2 from all the scores:
| Bob | |||
| Alice | Heads | Tails | |
| Heads | Alice: +1/2 Bob: -1/2 | Alice: -1/2 Bob: +1/2 | |
| Tails | Alice: -1/2 Bob: +1/2 | Alice: +1/2 Bob: -1/2 | |
But notice that we could just as well have re-scaled it to be zero sum by subtracting 1 from Alice's score:
| Bob | |||
| Alice | Heads | Tails | |
| Heads | Alice: 0 Bob: 0 | Alice: -1 Bob: 1 | |
| Tails | Alice: -1 Bob: 1 | Alice: 0 Bob: 0 | |
Notice that this is exactly the same game, but psychologically, we think of it much differently. In particular, the game now seems unfair to Alice: Bob only stands to gain, but Alice can lose! Just like I mentioned earlier, we're tempted to think of the game as if it's an interaction in which resources are exchanged.
I'm not saying this is a bad thing to think about. In real life, there are situations we can understand as games of resource exchange much more often than there are single-shot games where the payoffs are clearly identifiable in utility terms. I just want to emphasize that resource exchange is not what basic game theory is about, so you should be very careful not to confuse the two!
Now, as I mentioned earlier, we can also re-scale utilities without changing what they mean, and therefore, without changing the game:
| Bob | |||
| Alice | Heads | Tails | |
| Heads | Alice: 100 Bob: 0 | Alice: 0 Bob: 1 | |
| Tails | Alice: 0 Bob: 1 | Alice: 100 Bob: 0 | |
This game is equivalent to the others, and so, must still be "zero sum" in the technical sense of game theory! Despite this, it isn't even constant-sum.
So, how can we fix our concept of "zero sum" to better fit the underlying mathematical phenomenon?
Fixing "Zero Sum"
Since the underlying problem is that utilities are not comparable without further assumptions, an obvious solution would be to make the concept "zero sum" dependent on those further assumptions about how to compare utilities. The term "zero sum" and "constant sum" would then be meaningful (and meaningfully distinct), provided one specifies how to sum utilities.
I don't think that's the right route, however. I think it's better to look at what "zero sum" is trying to do, and come up with a concept which does that more effectively.
Linear Games
Here are diagrams of the four game matrices I used earlier:
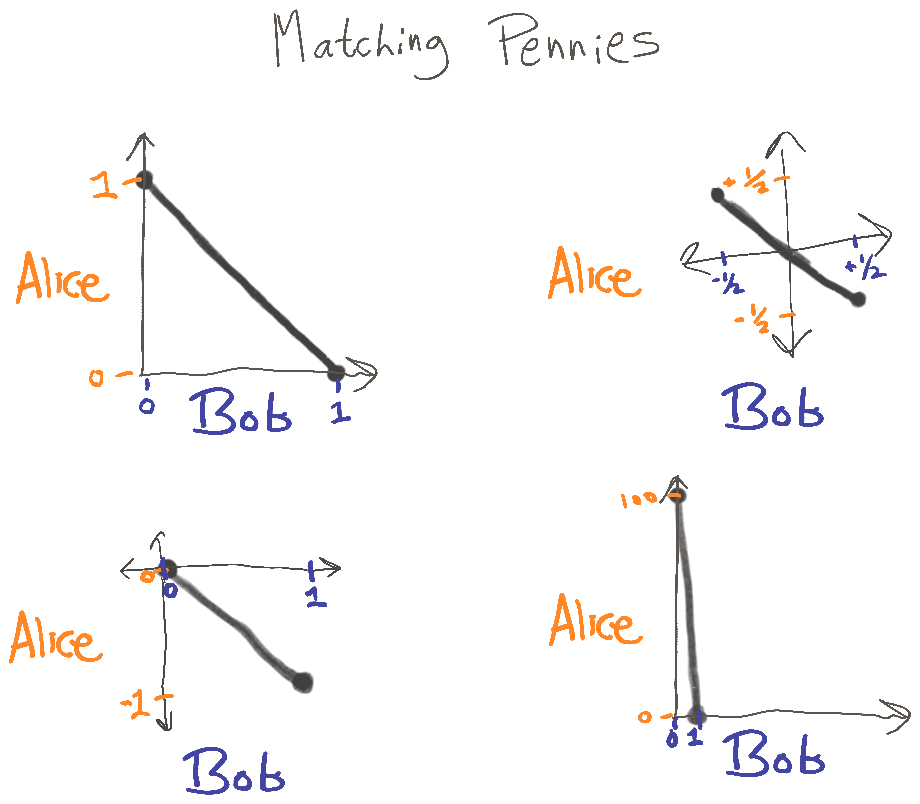
Clearly, any game matrix which is zero-sum will occupy the line. Similarly, any constant-sum game matrix will occupy a line where is the constant sum. But when we apply a positive multiplicative transformation, we get a line for positive constants . So what we can say about a zero-sum game which remains true regardless of transformations is outcomes fall on a line of negative slope.
Note that if outcomes fall on a line of positive slope, then the utility functions of the players must match up to inconsequential transforms. In other words, the two players must have the same preferences.
So, for two-player zero-sum linear games, there are just three choices: players can have equivalent preferences, or players can have completely opposed preferences (their utility functions being equivalent to the negative of each other), or some players can have no preferences (the slope of the line is zero or infinite).
For multi-player games, things get a little more complicated. Two players need not be perfectly aligned with or opposed to each other. In fact, any two-player game can be embedded in a zero-sum three-player game (and furthermore, any N-player game can be embedded in a N+1-player zero-sum game).
However, the concept of linear game still applies well to multi-player games, and we can still easily generalize the concept of zero-sum to linear games where the slope between any two dimensions is negative.
Linear games with negative slope are probably what you should interpret "zero sum" to mean in most formal game-theoretic contexts. This is, after, all, the most general thing that can be re-scaled to create an equivalent game which is literally zero-sum. However, we can still generalize further.
Completely Adversarial Games
In the original paper about the Nash bargaining problem (John Nash, The Bargaining Problem), Nash divides bargaining into two phases. In the first phase, players make threats: binding commitments about what they'll do if negotiations break down. In the second phase, players make demands: they ask for a specific level of resources. This demand is backed up by their earlier threats.
(Such an adversarial view of negotiation!)
The interesting thing for us here is that he observes that the threat portion of the game, if we consider it in isolation, is not zero sum, but might as well be: the payoff structure is just as adversarial. Because the outcome of the second part of the game is bound to be Pareto-optimal (under some assumptions about rational play), the choice of threats simply changes what trade-off will be arrived at along the Pareto-optimal surface:
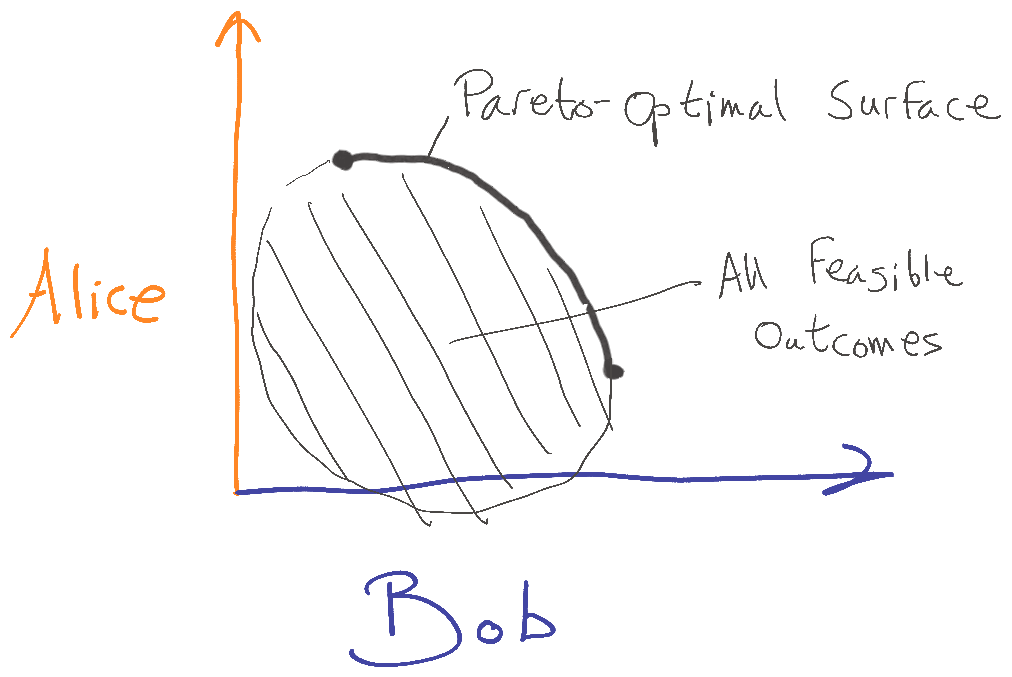
The feasible outcomes for the full game include Pareto improvements (otherwise there could not possibly be any gains due to bargaining), but when we assume optimal play for the "demand" step, the threat step considered in isolation has only Pareto-optimal outcomes.
So, we could consider a game completely adversarial if it has a structure like this: no strategy profiles are a Pareto improvement over any others. In other words, the feasible outcomes of the game equal the game's Pareto frontier. All possible outcomes involve trade-offs between players.
Note, however, that if we allow mixed strategies, the only completely adversarial games are the linear ones. This is because mixed strategies imply that the space of possible outcomes is convex. The convex hull of a Pareto frontier that's not already linear must have a nonempty interior, implying the possibility of Pareto improvements.
So, since it's rather common to assume there are mixed strategies, this generalization will usually not be giving you anything over "linear games of negative slope".
Notes on standard terminology and definitions.
I would have referred to my generalizations of zero sum as "adversarial games", and advocate "adversarial games" as an alternative to the problematic term "zero sum", except that "adversarial game" is a common term for non-cooperative game theory. Cooperative game-theory is game theory with enforceable contracts. Non-cooperative game theory is the version of game theory readers are most likely familiar with, IE, studying games with nash equilibria etc. Therefore, games like Prisoner's Dilemma, Stag Hunt, etc are "adversarial" or "non-cooperative" in the standard parlance, even though they are far from zero-sum.
So, I propose "completely adversarial" as the general term one should use as a replacement of "zero sum"; if someone asks you what this term means, you should say "there are no Pareto improvements in the set of possible outcomes" or something along those lines, and clarify that if we assume mixed strategies, this implies that the possible outcomes form a hyperplane.
In a comment, Vojta proposes "completely cooperative" to point to the opposite: a game where Pareto-domination forms a total order on the strategy profiles. He suggests "mixed-motive games" for games which are neither completely cooperative nor completely adversarial.
Note that if we assume mixed strategies, completely cooperative games are just linear games of strictly positive slope, the same way completely adversarial games must be linear (of negative slope) when we assume the existence of mixed strategies.
(Note also that my use of the term "linear" to describe games is, afaik, very nonstandard. It would be more precise for me to say "collinear", as in, all feasible points are collinear.)
The wikipedia article on zero-sum game uses the term "conflict game" for what I term "completely adversarial". Feel free to use that term if you like, but I find "completely adversarial" to be more satisfying.
Frustratingly, Wikipedia currently defines zero sum as a special case of constant sum, erroneously implying that we can sensibly differentiate between the two. In the same section, it goes on to name resource-redistribution transactions like theft and gambling as examples of zero-sum games, which (as I mentioned in the introduction) is often far from the case.
The article on zero sum games includes a discussion of avoiding a game, which asserts that if avoiding playing the game is an option, then it will always be an equilibrium strategy for one or both players. This further reinforces the idea that zero-sum games are considered as resource transfers, since presumably the idea is that at least one player has nothing to gain from a zero-sum interaction.
I'm not sure what terminology to suggest for the resource-transfer transactions which are usually referred to as zero sum, such as theft, political elections, etc. Maybe it's even fine to keep calling these "zero sum", using the term for what it intuitively invokes, since I'm already proposing that when discussing game theory we should use more technically accurate terms. But the risk is that you'll be mistakenly interpreted as invoking game theory.
There's a whole additional section I could write about how we can try to formally understand what these resource-transfer situations even are, and what it means for them to be "zero sum" in the intuitive sense, but I think I will leave things here for now.