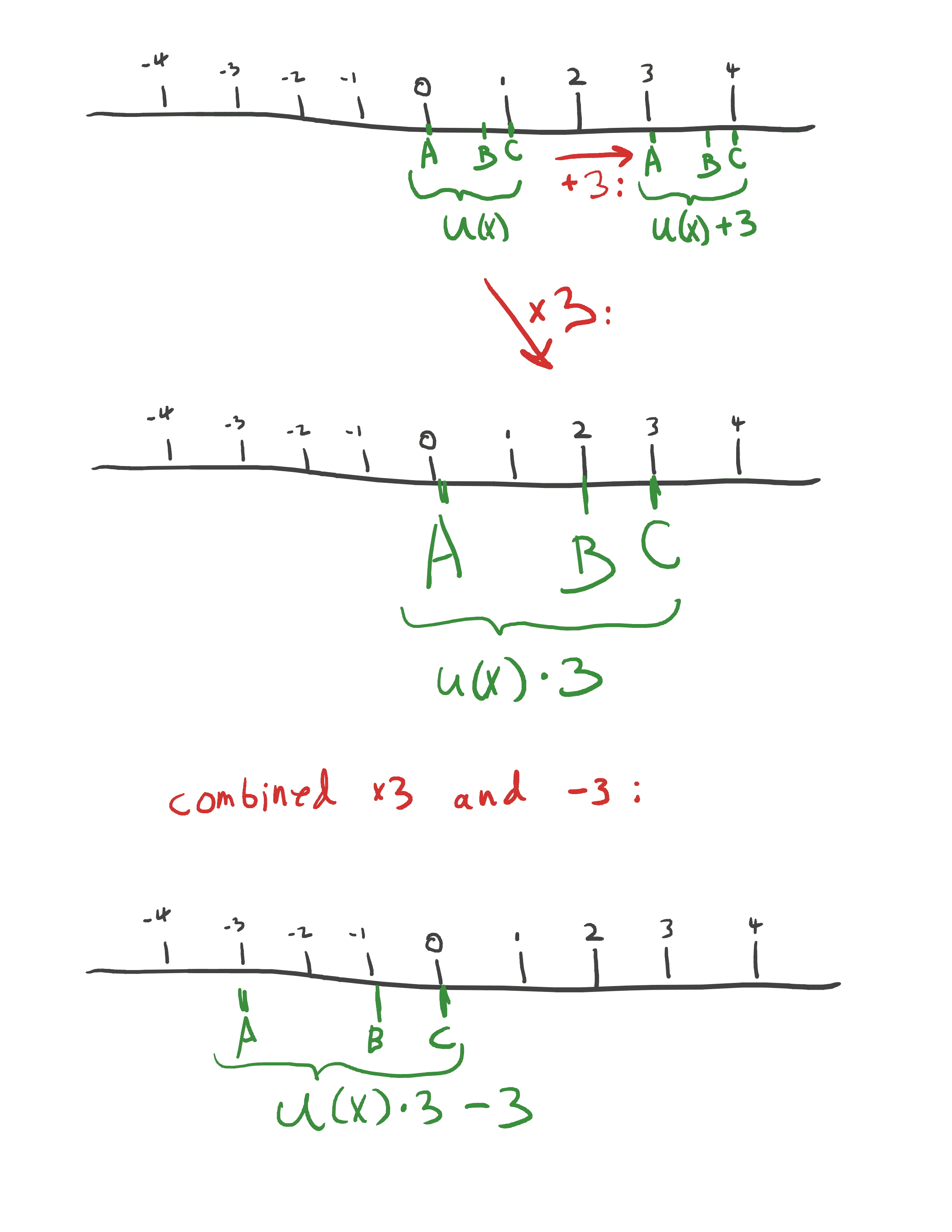Comparing Utilities
10Vanessa Kosoy
3abramdemski
9evhub
4abramdemski
4evhub
8Slider
2abramdemski
5habryka
2abramdemski
2abramdemski
7habryka
3romeostevensit
4abramdemski
2Rohin Shah
2Charlie Steiner
New Comment
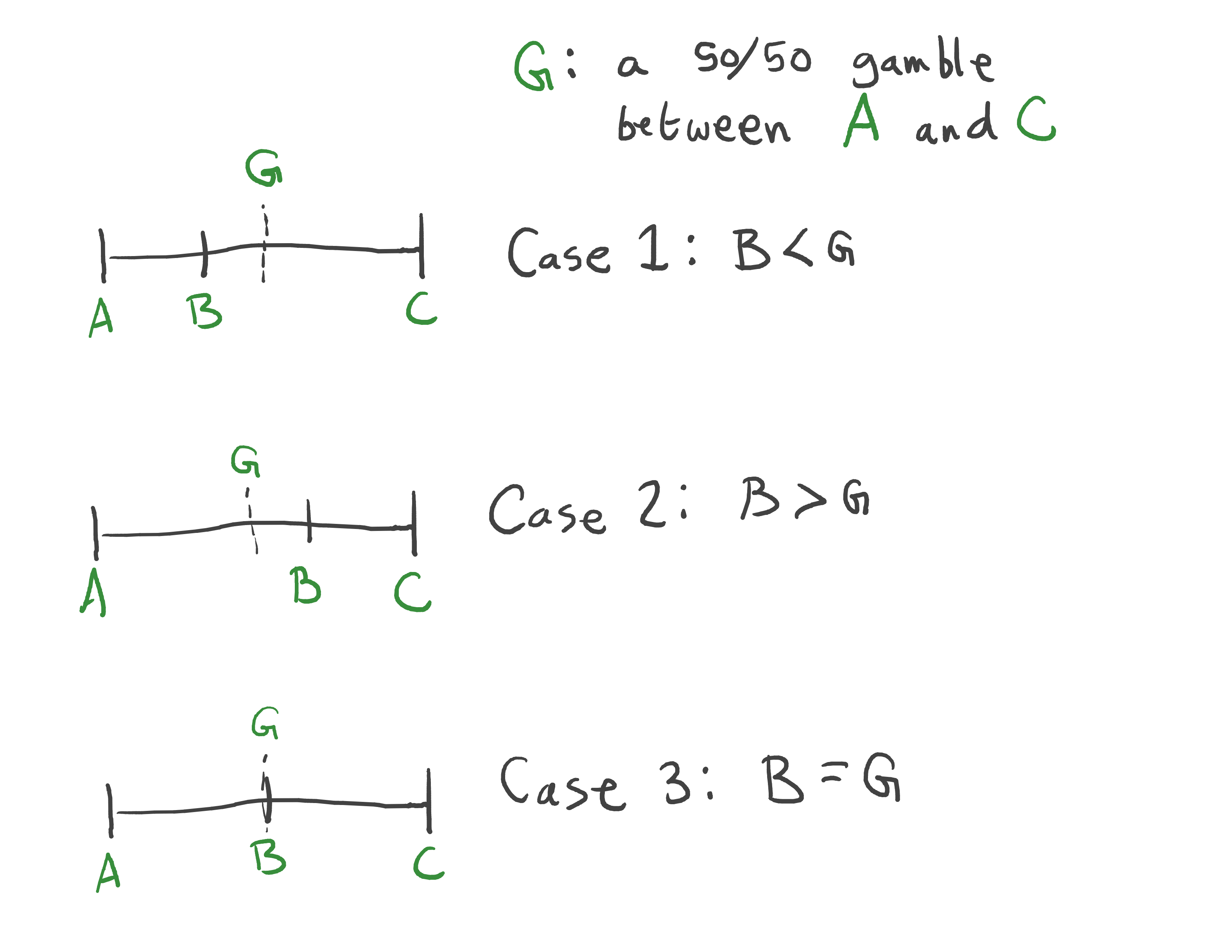
I suspect most readers will not find the KS solution to be more intuitively appealing?
The problem in your example is that you failed to identify a reasonable disagreement point. In the situation you described is the disagreement point since every agent can guarantee emself a payoff of unilaterally, so the KS solution is also (since the disagreement point is already on the Pareto frontier).
In general it is not that obvious what the disagreement point should be, but maximin payoffs is one natural choice. Nash equilibrium is the obvious alternative, but it's not clear what to do if we have several.
For applications such as voting and multi-user AI alignment that's less natural since, even if we know the utility functions, it's not clear what action spaces should we consider. In that case a possible choice of disagreement point is maximizing the utility of a randomly chosen participant. If the problem can be formulated as partitioning resources, then the uniform partition is another natural choice.
The problem in your example is that you failed to identify a reasonable disagreement point.
Ahh, yeahh, that's a good point.
If we simply take the fixed point, Primus is going to get the short end of the stick all the time: because Primus cares about everyone else more, everyone else cares about Primus' personal preferences less than anyone else's.
Simply put, I don't think more altruistic individuals should be punished! In this setup, the "utility monster" is the perfectly selfish individual. Altruists will be scrambling to help this person while the selfish person does nothing in return.
I'm not sure why you think this is a problem. Supposing you want to satisfy the group's preferences as much as possible, shouldn't you care about Primus less since Primus will be more satisfied just from you helping the others? I agree that this can create perverse incentives in practice, but that seems like the sort of thing that you should be handling as part of your decision theory, not your utility function.
A different way to do things is to interpret cofrences as integrating only the personal preferences of the other person.
I feel like the solution of having cofrences not count the other person's cofrences just doesn't respect people's preferences—when I care about the preferences of somebody else, that includes caring about the preferences of the people they care about. It seems like the natural solution to this problem is to just cut things off when you go in a loop—but that's exactly what taking the fixed point does, which seems to reinforce the fixed point as the right answer here.
I agree that this can create perverse incentives in practice, but that seems like the sort of thing that you should be handling as part of your decision theory, not your utility function.
I'm mainly worried about the perverse incentives part.
I recognize that there's some weird level-crossing going on here, where I'm doing something like mixing up the decision theory and the utility function. But it seems to me like that's just a reflection of the weird muddy place our values come from?
You can think of humans a little like self-modifying AIs, but where the modification took place over evolutionary history. The utility function which we eventually arrived at was (sort of) the result of a bargaining process between everyone, and which took some accounting of things like exploitability concerns.
In terms of decision theory, I often think in terms of a generalized NicerBot: extend everyone else the same cofrence-coefficient they extend to you, plus an epsilon (to ensure that two generalized NicerBots end up fully cooperating with each other). This is a pretty decent strategy for any game, generalizing from one of the best strategies for Prisoner's Dilemma. (Of course there is no "best strategy" in an objective sense.)
But a decision theory like that does mix levels between the decision theory and the utility function!
I feel like the solution of having cofrences not count the other person's cofrences just doesn't respect people's preferences—when I care about the preferences of somebody else, that includes caring about the preferences of the people they care about.
I totally agree with this point; I just don't know how to balance it against the other point.
A crux for me is the coalition metaphor for utilitarianism. I think of utilitarianism as sort of a natural endpoint of forming beneficial coalitions, where you've built a coalition of all life.
If we imagine forming a coalition incrementally, and imagine that the coalition simply averages utility functions with its new members, then there's an incentive to join the coalition as late as you can, so that your preferences get the largest possible representation. (I know this isn't the same problem we're talking about, but I see it as analogous, and so a point in favor of worrying about this sort of thing.)
We can correct that by doing 1/n averaging: every time the coalition gains members, we make a fresh average of all member utility functions (using some utility-function normalization, of course), and everybody voluntarily self-modifies to have the new mixed utility function.
But the problem with this is, we end up punishing agents for self-modifying to care about us before joining. (This is more closely analogous to the problem we're discussing.) If they've already self-modified to care about us more before joining, then their original values just get washed out even more when we re-average everyone.
So really, the implicit assumption I'm making is that there's an agent "before" altruism, who "chose" to add in everyone's utility functions. I'm trying to set up the rules to be fair to that agent, in an effort to reward agents for making "the altruistic leap".
But a decision theory like that does mix levels between the decision theory and the utility function!
I agree, though it's unclear whether that's an actual level crossing or just a failure of our ability to be able to properly analyze that strategy. I would lean towards the latter, though I am uncertain.
A crux for me is the coalition metaphor for utilitarianism. I think of utilitarianism as sort of a natural endpoint of forming beneficial coalitions, where you've built a coalition of all life.
This is how I think about preference utilitarianism but not how I think about hedonic utilitarianism—for example, a lot of what I value personally is hedonic-utilitarianism-like, but from a social perspective, I think preference utilitarianism is a good Schelling point for something we can jointly agree on. However, I don't call myself a preference utilitarian—rather, I call myself a hedonic utilitarian—because I think of social Schelling points and my own personal values as pretty distinct objects. And I could certainly imagine someone who terminally valued preference utilitarianism from a personal perspective—which is what I would call actually being a preference utilitarian.
Furthermore, I think that if you're actually a preference utilitarian vs. if you just think preference utilitarianism is a good Schelling point, then there are lots of cases where you'll do different things. For example, if you're just thinking about preference utilitarianism as a useful Schelling point, then you want to carefully consider the incentives that it creates—such as the one that you're pointing to—but if you terminally value preference utilitarianism, then that seems like a weird thing to be thinking about, since the question you should be thinking about in that context should be more like what is it about preferences that you actually value and why.
If we imagine forming a coalition incrementally, and imagine that the coalition simply averages utility functions with its new members, then there's an incentive to join the coalition as late as you can, so that your preferences get the largest possible representation. (I know this isn't the same problem we're talking about, but I see it as analogous, and so a point in favor of worrying about this sort of thing.)
We can correct that by doing 1/n averaging: every time the coalition gains members, we make a fresh average of all member utility functions (using some utility-function normalization, of course), and everybody voluntarily self-modifies to have the new mixed utility function.
One thing I will say here is that usually when I think about socially agreeing on a preference utilitarian coalition, I think about doing so from more of a CEV standpoint, where the idea isn't just to integrate the preferences of agents as they currently are, but as they will/should be from a CEV perspective. In that context, it doesn't really make sense to think about incremental coalition forming, because your CEV (mostly, with some exceptions) should be the same regardless of what point in time you join the coalition.
But the problem with this is, we end up punishing agents for self-modifying to care about us before joining. (This is more closely analogous to the problem we're discussing.) If they've already self-modified to care about us more before joining, then their original values just get washed out even more when we re-average everyone.
I guess this just seems like the correct outcome to me. If you care about the values of the coalition, then the coalition should care less about your preferences, because they can partially satisfy them just by doing what the other people in the coalition want.
So really, the implicit assumption I'm making is that there's an agent "before" altruism, who "chose" to add in everyone's utility functions. I'm trying to set up the rules to be fair to that agent, in an effort to reward agents for making "the altruistic leap".
It certainly makes sense to reward agents for choosing to instrumentally value the coalition—and I would include instrumentally choosing to self-modify yourself to care more about the coalition in that—but I'm not sure why it makes sense to reward agents for terminally valuing the coalition—that is, terminally valuing the coalition independently of any decision theoretic considerations that might cause you to instrumentally modify yourself to do so.
Again, I think this makes more sense from a CEV perspective—if you instrumentally modify yourself to care about the coalition for decision-theoretic reasons, that might change your values, but I don't think that it should change your CEV. In my view, your CEV should be about your general strategy for how to self-modify yourself in different situations rather than the particular incarnation of you that you've currently modified to.
This jumps from mathematical consistency to a kind of opinion when pareto improvement enters the picture. Sure if we have choice between two social policies and everyone prefers one over the other because their personal lot is better there is no conflict on the order. This could be warranted if for some reason we needed consensus to get a "thing passed". However where there is true conflict it seems to say that a "good" social policy can't be formed.
To be somewhat analogous with "utility monster", construct a "consensus spoiler". He exactly prefers what everyone anti-prefers, having a coference of -1 for everyone. If someone would gain something he is of the opinion that he losses. So no pareto improvements are possible. If you have a community of 100 agents that would agree to pick some states over others and construct a new comunity of 101 with the consensus spoiler then they can't form any choice function. The consensus spoiler is in effect maximally antagonistic towards everything else. The question whether it is warranted, allowed or forbidden that the coalition of 100 just proceeds with the policy choice that screws the spoiler over doesn't seem to be a mathematical kind of claim.
And even in the less extreme degree I don't get how you could use this setup to judge values that are in conflict. And if you encounter a unknown agent it seems it is ambigious whether you should take heed of its values in compromise or just treat it as a possible enemy and just adhere to your personal choices.
Yeah, I like your "consensus spoiler". Maybe needs a better name, though... "Contrarian Monster"?
having a coference of -1 for everyone.
This way of defining the Consensus Spoiler seems needlessly assumption-heavy, since it assumes not only that we can already compare utilities in order to define this perfect antagonism, but furthermore that we've decided how to deal with cofrences.
A similar option with a little less baggage is to define it as having the opposite of the preferences of our social choice function. They just hate whatever we end up choosing to represent the group's preferences.
A simpler option is just to define the Contrarian Monster as having opposite preferences from one particular member of the collective. (Any member will do.) This ensures that there can be no Pareto improvements.
If you have a community of 100 agents that would agree to pick some states over others and construct a new comunity of 101 with the consensus spoiler then they can't form any choice function.
Actually, the conclusion is that you can form any social choice function. Everything is "Pareto optimal".
The question whether it is warranted, allowed or forbidden that the coalition of 100 just proceeds with the policy choice that screws the spoiler over doesn't seem to be a mathematical kind of claim.
If we think of it as bargaining to form a coalition, then there's never any reason to include the Spoiler in a coalition (especially if you use the "opposite of whatever the coalition wants" version). In fact, there is a version of Harsanyi's theorem which allows for negative weights, to allow for this -- giving an ingroup/outgroup sort of thing. Usually this isn't considered very seriously for definitions of utilitarianism. But it could be necessary in extreme cases.
(Although putting zero weight on it seems sufficient, really.)
And even in the less extreme degree I don't get how you could use this setup to judge values that are in conflict.And if you encounter a unknown agent it seems it is ambigious whether you should take heed of its values in compromise or just treat it as a possible enemy and just adhere to your personal choices.
Pareto-optimality doesn't really give you the tools to mediate conflicts, it's just an extremely weak condition on how you do so, which says essentially that we shouldn't put negative weight on anyone.
Granted, the Consensus Spoiler is an argument that Pareto-optimality may not be weak enough, in extreme situations.
Yep, fixed. Thank you!
Judging from the URL of those links, those images were hosted on a domain that you could access, but others could not, namely they were stored as Gmail image attachments, to which of course you as the recipient have access, but random LessWrong users do not.
Type theory for utility hypothesis: there are a certain distinct (small) number of pathways in the body that cause physical good feelings. Map those plus the location, duration, intensity, and frequency dimensions and you start to have comparability. This doesn't solve the motivation/meaning structures built on top of those pathways which have more degrees of freedom, but it's still a start. Also, those more complicated things built on top might just be scalar weightings and not change the dimensionality of the space.
Yeah, it seems like in practice humans should be a lot more comparable than theoretical agentic entities like I discuss in the post.
Planned summary for the Alignment Newsletter:
This is a reference post about preference aggregation across multiple individually rational agents (in the sense that they have VNM-style utility functions), that explains the following points (among others):
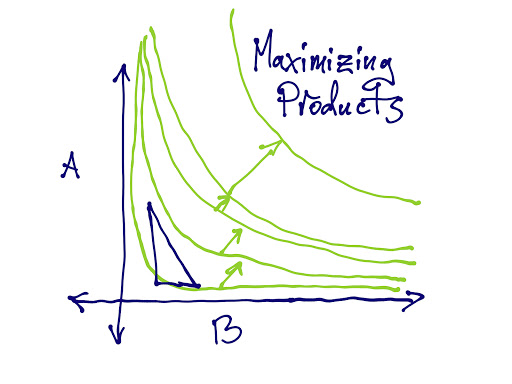
1. The concept of “utility” in ethics is somewhat overloaded. The “utility” in hedonic utilitarianism is very different from the VNM concept of utility. The concept of “utility” in preference utilitarianism is pretty similar to the VNM concept of utility.
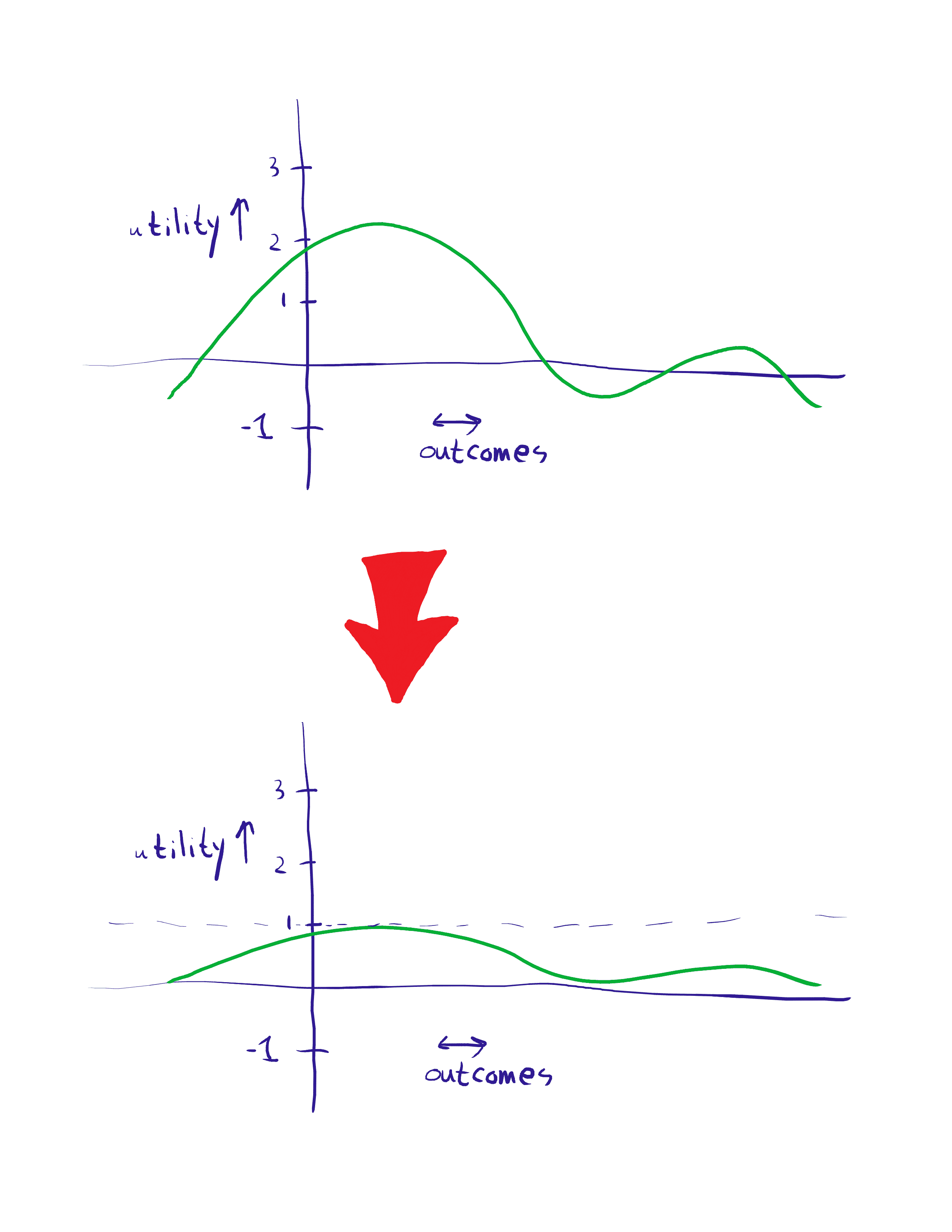
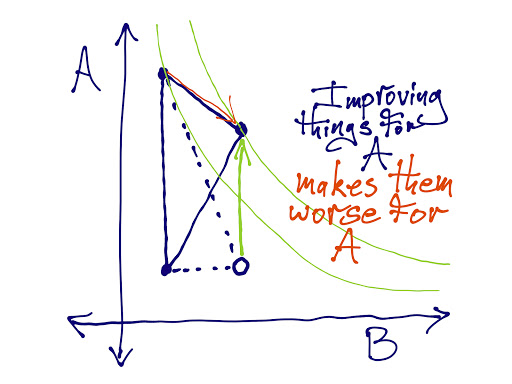
2. Utilities are not directly comparable, because affine transformations of utility functions represent exactly the same set of preferences. Without any additional information, concepts like “utility monster” are type errors.
3. However, our goal is not to compare utilities, it is to aggregate people’s preferences. We can instead impose constraints on the aggregation procedure.
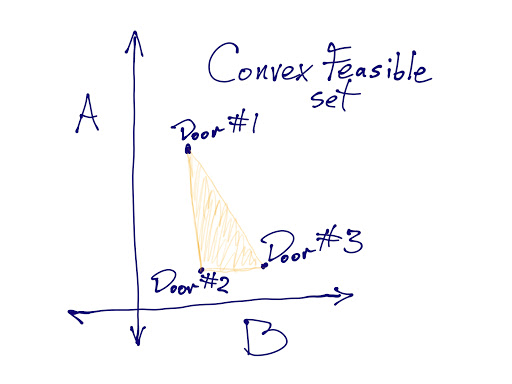
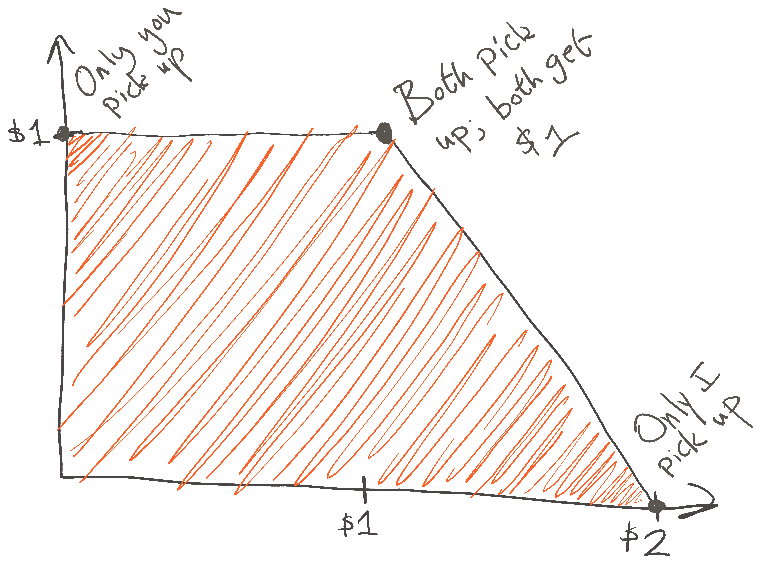
4. If we require that the aggregation procedure produces a Pareto-optimal outcome, then Harsanyi’s utilitarianism theorem says that our aggregation procedure can be viewed as maximizing some linear combination of the utility functions.
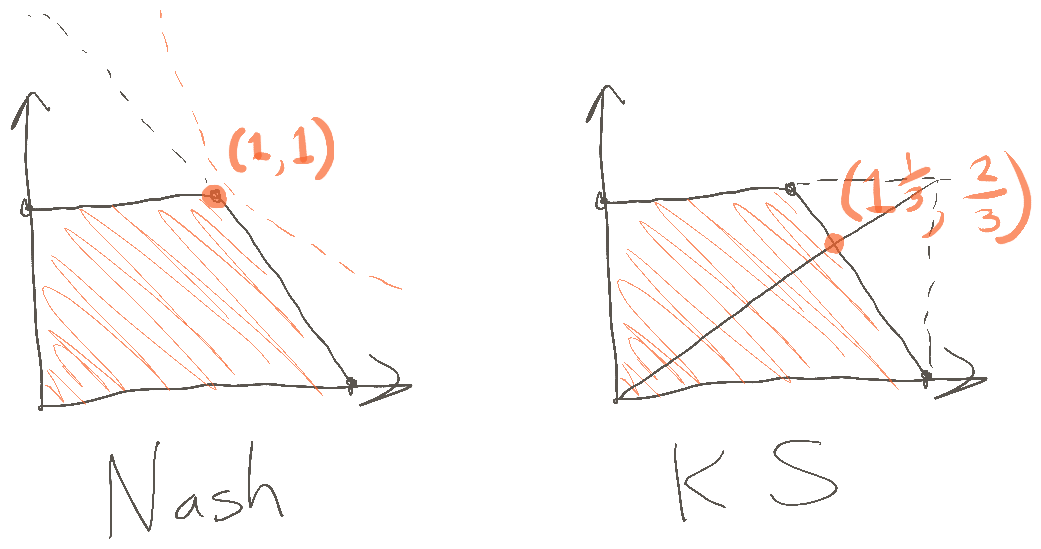
5. We usually want to incorporate some notion of fairness. Different specific assumptions lead to different results, including variance normalization, Nash bargaining, and Kalai-Smorodinsky.
One think I'd also ask about is: what about ecology / iterated games? I'm not very sure at all whether there are relevant iterated games here, so I'm curious what you think.
How about an ecology where there are both people and communities - the communities have different aggregation rules, and the people can join different communities. There's some set of options that are chosen by the communities, but it's the people who actually care about what option gets chosen and choose how to move between communities based on what happens with the options - the communities just choose their aggregation rule to get lots of people to join them.
How can we set up this game so that interesting behavior emerges? Well, people shouldn't just seek out the community that most closely matches their own preferences, because then everyone would fracture into communities of size 1. Instead, there must be some benefit to being in a community. I have two ideas about this: one is that the people could care to some extent about what happens in all communities, so they will join a community if they think they can shift its preferences on the important things while conceding the unimportant things. Another is that there could be some crude advantage to being in a community that looks like a scaling term (monotonically increasing with community size) on how effective they are at satisfying their peoples' preferences.
Curated and popular this week