Thanks for this! I like your concept of APS systems; I think I might use that going forward. I think this document works as a good "conservative" (i.e. optimistic) case for worrying about AI risk. As you might expect, I think the real chances of disaster are higher. For more on why I think this, well, there are the sequences of posts I wrote and of course I'd love to chat with you anytime and run some additional arguments by you.
For now I'll just say: 5% total APS risk (seems to me to) fail a sanity check, as follows:
1. There's at least an X% chance of APS systems being made by 2035. (I think X = 60 and I think it's unreasonable to have X<30 (and I'm happy to say more about why) but you'll probably agree X is at least 10, right?)
2. Conditional on that happening, it seems like the probability of existential catastrophe is quite high, like 50% or so. (Conditional on APS happening that soon, takeoff is likely to be relatively fast, and there won't have been much time to do alignment research, and more generally the optimistic slow takeoff picture in which we get lots of nice scary warning shots and society has lots of time to react will just not be true)
3. Therefore the probability of doom-by-APS-by-2035 is at least 0.5X, so at least 5%.
4. Therefore the probability of doom-by-APS-by-2070 must be significantly higher than 5%.
Also: It seems that most of your optimism comes from assigning only 40%*65%*40% ~= 10% chance to the combined claim "Conditional it being both possible and strongly incentivized to build APS systems, APS systems will end up disempowering approximately all of humanity." This to me sounds like you basically have 90% credence that the alignment problem will be solved and implemented successfully in time, in worlds where the problem is real (i.e. APS systems are possible and incentivized). I feel like it's hard for me to be that confident, considering how generally shitty the world is at solving problems even when they are obvious and simple and killing people every day and the solution is known, and considering how this problem is disputed and complex and won't be killing people until it is either already too late or almost and the solution is not known. Perhaps a related argument would be: Couldn't you run your same arguments to conclude that the probability of nuclear war in the past 100 years was about 10%? And don't we have good reason to think that in fact the probability was higher than that and we just got lucky? (See: the history of close calls, plus independently the anthropic shadow stuff)
Hi Daniel,
Thanks for reading. I think estimating p(doom) by different dates (and in different take-off scenarios) can be a helpful consistency check, but I disagree with your particular “sanity check” here -- and in particular, premise (2). That is, I don’t think that conditional on APS-systems becoming possible/financially feasible by 2035, it’s clear that we should have at least 50% on doom (perhaps some of disagreement here is about what it takes for the problem to be "real," and to get "solved"?). Nor do I see 10% on “Conditional it being both possible and strongly incentivized to build APS systems, APS systems will end up disempowering approximately all of humanity” as obviously overconfident (though I do take some objections in this vein seriously). I’m not sure exactly what “10% on nuclear war” analog argument you have in mind: would you be able to sketch it out, even if hazily?
Thanks for the thoughtful reply. Here are my answers to your questions:
Here is what you say in support of your probability judgment of 10% on "Conditional it being both possible and strongly incentivized to build APS systems, APS systems will end up disempowering approximately all of humanity."
Beyond this, though, I’m also unsure about the relative difficulty of creating practically PS-aligned systems, vs. creating systems that would be practically PS-misaligned, if deployed, but which are still superficially attractive to deploy. One commonly cited route to this is via a system actively pretending to be more aligned than it is. This seems possible, and predictable in some cases; but it’s also a fairly specific behavior, limited to systems with a particular pattern of incentives (for example, they need to be sufficiently non-myopic to care about getting deployed, there need to be sufficient benefits to deployment, and so on), and whose deception goes undetected. It’s not clear to me how common to expect this to be, especially given that we’ll likely be on the lookout for it.
More generally, I expect decision-makers to face various incentives (economic/social backlash, regulation, liability, the threat of personal harm, and so forth) that reduce the attraction of deploying systems whose practical PS-alignment remains significantly uncertain. And absent active/successful deception, I expect default forms of testing to reveal many PS-alignment problems ahead of time.
...
The 35% on this premise being false comes centrally from the fact that (a) I expect us to have seen a good number of warning shots before we reach really high-impact practical PS-alignment failures, so this premise requires that we haven’t responded to those adequately, (b) the time-horizons and capabilities of the relevant practically PS-misaligned systems might be limited in various ways, thereby reducing potential damage, and (c) practical PS-alignment failures on the scale of trillions of dollars (in combination) are major mistakes, which relevant actors will have strong incentives, other things equal, to avoid/prevent (from market pressure, regulation, self-interested and altruistic concern, and so forth).
...
I’m going to say: 40%. There’s a very big difference between >$1 trillion dollars of damage (~6 Hurricane Katrinas), and the complete disempowerment of humanity; and especially in slower take-off scenarios, I don’t think it at all a foregone conclusion that misaligned power-seeking that causes the former will scale to the latter.
As I read it, your analysis is something like: Probably these systems won't be actively trying to deceive us. Even if they are, we'll probably notice it and stop it since we'll be on the lookout for it. Systems that may not be aligned probably won't be deployed, because people will be afraid of dangers, thanks to warning shots. Even if they are deployed, the damage will probably be limited, since probably even unaligned systems won't be willing and able to completely disempower humanity.
My response is: This just does not seem plausible conditional on it all happening by 2035. I think I'll concede that the issue of whether they'll be trying to deceive us is independent of whether timelines are short or long. However, in short-timelines scenarios there will be fewer (I would argue zero) warning shots, and less time for AI risk to be taken seriously by all the prestigious people. Moreover, takeoff is likely to be fast, with less time for policymakers and whatnot to react and less time for overseers to study and analyze their AIs. I think I'll also concede that timelines is not correlated with willingness to disempower humanity, but it's correlated with ability, due to takeoff speed considerations -- if timelines are short, then when we get crazy AI we'll be able to get crazier AI quickly by scaling up a bit more, and also separately it probably takes less time to "cross the human range." Moreover, if timelines are short then we should expect prestigious people, institutions, etc. to be as collectively incompetent as they are today--consider how COVID was handled and is still being handled. Even if we get warning shots, I don't expect the reactions to them to help much, instead simply patch over problems and maybe delay doom for a bit. AI risk stuff will become a polarized partisan political issue with lots of talking heads yelling at each other and lots of misguided people trying to influence the powers that be to do this or that. In that environment finding the truth will be difficult, and so will finding and implementing the correct AI-risk-reducing policies.
My nuclear winter argument was, at a high level, something like: Your argument for 10% is pretty general, and could be used to argue for <10% risk for a lot of things, e.g. nuclear war. Yet empirically the risk for those things is higher than that.
Your argument as applied to nuclear war would be something like: Probably nations won't build enough nuclear weapons to cause nuclear winter. Even if they do, they wouldn't set up systems with a risk of accident, since there would be warning shots and people would be afraid of the dangers. Even if there is a failure and a nuke is set off, it probably wouldn't lead to nuclear winter since decision-makers would deescalate rather than escalate.
I would say: The probability of nuclear winter this century was higher than 10%, and moreover, nuclear winter is a significantly easier-to-avoid problem than APR-AI risk IMO, because psychologically and culturally it's a lot easier to convince people that nukes are dangerous and that they shouldn't be launched and that there should be lots of redundant safeguards on them than that [insert newest version of incredibly popular and profitable AI system here] is dangerous and shouldn't be deployed or even built in the first place. Moreover it's a lot easier, technically, to put redundant safeguards on nuclear weapons than to solve the alignment problem!
Nuclear winter was just the first thing that came to mind, but my argument would probably be a lot stronger if I chose other examples. The general idea is that on my reading of history, preventing APR-AI risk is just a lot harder, a lot less likely to succeed, than preventing various other kinds of risk, some of which in fact happened or very nearly happened.
Hi Daniel,
Thanks for taking the time to clarify.
One other factor for me, beyond those you quote, is the “absolute” difficulty of ensuring practical PS-alignment, e.g. (from my discussion of premise 3):
Part of this uncertainty has to do with the “absolute” difficulty of achieving practical PS-alignment, granted that you can build APS systems at all. A system’s practical PS-alignment depends on the specific interaction between a number of variables -- notably, its capabilities (which could themselves be controlled/limited in various ways), its objectives (including the time horizon of the objectives in question), and the circumstances it will in fact exposed to (circumstances that could involve various physical constraints, monitoring mechanisms, and incentives, bolstered in power by difficult-to-anticipate future technology, including AI technology). I expect problems with proxies and search to make controlling objectives harder; and I expect barriers to understanding (along with adversarial dynamics, if they arise pre-deployment) to exacerbate difficulties more generally; but even so, it also seems possible to me that it won’t be “that hard” (by the time we can build APS systems at all) to eliminate many tendencies towards misaligned power-seeking (for example, it seems plausible to me that selecting very strongly against (observable) misaligned power-seeking during training goes a long way), conditional on retaining realistic levels of control over a system’s post-deployment capabilities and circumstances (though how often one can retain this control is a further question).
My sense is that relative to you, I am (a) less convinced that ensuring practical PS-alignment will be “hard” in this absolute sense, once you can build APS systems at all (my sense is that our conceptions of what it takes to “solve the alignment problem” might be different), (b) less convinced that practically PS-misaligned systems will be attractive to deploy despite their PS-misalignment (whether because of deception, or for other reasons), (c) less convinced that APS systems becoming possible/incentivized by 2035 implies “fast take-off” (it sounds like you’re partly thinking: those are worlds where something like the scaling hypothesis holds, and so you can just keep scaling up; but I don’t think the scaling hypothesis holding to an extent that makes some APS systems possible/financially feasible implies that you can just scale up quickly to systems that can perform at strongly superhuman levels on e.g. ~any task, whatever the time horizons, data requirements, etc), and (d) more optimistic about something-like-present-day-humanity’s ability to avoid/prevent failures at a scale that disempower ~all of humanity (though I do think Covid, and its policitization, an instructive example in this respect), especially given warning shots (and my guess is that we do get warning shots both before or after 2035, even if APS systems become possible/financially feasible before then).
Re: nuclear winter, as I understand it, you’re reading me as saying: “in general, if a possible and incentivized technology is dangerous, there will be warning shots of the dangers; humans (perhaps reacting to those warning shots) won’t deploy at a level that risks the permanent extinction/disempowerment of ~all humans; and if they start to move towards such disempowerment/extinction, they’ll take active steps to pull back.” And your argument is: “if you get to less than 10% doom on this basis, you’re going to give too low probabilities on scenarios like nuclear winter in the 20th century.”
I don’t think of myself as leaning heavily on an argument at that level of generality (though maybe there’s a bit of that). For example, that statement feels like it’s missing the “maybe ensuring practical PS-alignment just isn’t that hard, especially relative to building practically PS-misaligned systems that are at least superficially attractive to deploy” element of my own picture. And more generally, I expect to say different things about e.g. biorisk, climate change, nanotech, etc, depending on the specifics, even if generic considerations like “humans will try not to all die” apply to each.
Re: nuclear winter in particular, I’d want to think a bit more about what sort of probability I’d put on nuclear winter in the 20th century (one thing your own analysis skips is the probability that a large nuclear conflict injects enough smoke into the stratosphere to actually cause nuclear winter, which I don’t see as guaranteed -- and we’d need to specify what level of cooling counts). And nuclear winter on its own doesn’t include a “scaling to the permanent disempowerment/extinction of ~all of humanity” step -- a step that, FWIW, I see as highly questionable in the nuclear winter case, and which is important to my own probability on AI doom (see premise 5). And there are various other salient differences: for example, mutually assured destruction seems like a distinctly dangerous type of dynamic, which doesn’t apply to various AI deployment scenarios; nuclear weapons have widespread destruction as their explicit function, whereas most AI systems won’t; and so on. That said, I think comparisons in this vein could still be helpful; and I’m sympathetic to points in the vein of “looking at the history of e.g. climate, nuclear risk, BSL-4 accidents, etc the probability that humans will deploy technology that risks global catastrophe, and not stop doing so even after getting significant evidence about the risks at stake, can’t be that low” (I talk about this a bit in 4.4.3 and 6.2).
I commented a portion of a copy of your power-seeking writeup.
I like the current doc a lot. I also feel that it seems to not consider some big formal hints and insights we've gotten from my work over the past two years.[1]
Very recently, I was able to show the following strong result:
Some researchers have speculated that capable reinforcement learning (RL) agents are often incentivized to seek resources and power in pursuit of their objectives. While seeking power in order to optimize a misspecified objective, agents might be incentivized to behave in undesirable ways, including rationally preventing deactivation and correction. Others have voiced skepticism: human power-seeking instincts seem idiosyncratic, and these urges need not be present in RL agents. We formalize a notion of power within the context of Markov decision processes (MDPs). We prove sufficient conditions for when optimal policies tend to seek power over the environment. For most prior beliefs one might have about the agent's reward function, one should expect optimal agents to seek power by keeping a range of options available and, when the discount rate is sufficiently close to 1, by preferentially retaining access to more terminal states. In particular, these strategies are optimal for most reward functions.
I'd be interested in discussing this more with you; the result isn't publicly available yet, but I'd be happy to take time to explain it. The result tells us significant things about generic optimal behavior in the finite MDP setting, and I think it's worth deciphering these hints as best we can to apply them to more realistic training regimes.
For example, if you train a generally intelligent RL agent's reward predictor network on a curriculum of small tasks, my theorems prove that these small tasks are probably best solved by seeking power within the task. This is an obvious way the agent might notice the power abstraction, become strategically aware, and start pursuing power instrumentally.
Another angle to consider is, how do power-seeking tendencies mirror other convergent phenomena, like convergent evolution, universal features, etc, and how does this inform our expectations about PS agent cognition? As in the MDP case, I suspect that similar symmetry-based considerations are at play.
For example, consider a DNN being trained on a computer vision task. These networks often learn edge detectors in early layers (this also occurs in the visual cortex). So fix the network architecture, data distribution, loss function, and the edge detector weights. Now consider a range of possible label distributions; for each, consider the network completion which minimizes expected loss. You could also consider the expected output of some learning algorithm, given that it finetunes the edge detector network for some number of steps. I predict that for a wide range of "reasonable" label distributions, these edge detectors promote effective loss minimization, more so than if these weights were randomly set. In this sense, having edge detectors is "empowering."
And the reason this might crop up is that having these early features is a good idea for many possible symmetries of the label distribution. My thoughts here are very rough at this point in time, but I do feel like the analysis would benefit from highlighting parallels to convergent evolution, etc.
(This second angle is closer to conceptual alignment research than it is to weighing existing work, but I figured I'd mention it.)
Great writeup, and I'd love to chat some time if you're available.
[1] My work has revolved around formally understanding power-seeking in a simple setting (finite MDPs) so as to inform analyses like these. Public posts include:
I have two comments on section 4:
This section examines why we might expect it to be difficult to create systems of this kind that don’t seek to gain and maintain power in unintended ways.
First, I like your discussion in section 4.3.3. The option of controlling circumstances is too often overlooked I feel.
However, your further analysis of the level of difficulty seems to be based mostly on the assumption that we must, or at least will, treat an AI agent as a black box that is evolved, rather than designed. Section 4.5:
[full alignment] is going to be very difficult, especially if we build them by searching over systems that satisfy external criteria, but which we don’t understand deeply, and whose objectives we don’t directly control.
There is a whole body of work which shows that evolved systems are often power-seeking. But at the same time within the ML and AI safety literature, there is also a second body of work on designing systems which are not power seeking at all, or have limited power seeking incentives, even though they contain a machine-learning subsystem inside them. I feel that you are ignoring the existence and status of this second body of work in your section 4 overview, and that this likely creates a certain negative bias in your estimates later on.
Some examples of designs that explicitly try to avoid or cap power-seeking are counterfactual oracles, and more recently imitation learners like this one, and my power-limiting safety interlock here. All of these have their disadvantages and failure modes, so if you are looking for perfection they would disappoint you, but if you are looking for tractable x-risk management, I feel there is reason for some optimism.
BTW, the first page of chapter 7 of Russell's Human Compatible makes a similar point, flatly declaring that we would be toast if we made the mistake of viewing our task as controlling a black box agent that was given to us.
Hi Koen,
Glad to hear you liked section 4.3.3. And thanks for pointing to these posts -- I certainly haven't reviewed all the literature, here, so there may well be reasons for optimism that aren't sufficiently salient to me.
Re: black boxes, I do think that black-box systems that emerge from some kind of evolution/search process are more dangerous; but as I discuss in 4.4.1, I also think that the bare fact that the systems are much more cognitively sophisticated than humans creates significant and safety-relevant barriers to understanding, even if the system has been designed/mechanistically understood at a different level.
Re: “there is a whole body of work which shows that evolved systems are often power-seeking” -- anything in particular you have in mind here?
Re: “there is a whole body of work which shows that evolved systems are often power-seeking” -- anything in particular you have in mind here?
For AI specific work, the work by Alex Turner mentioned elsewhere in this comment section comes to mind, as backing up a much larger body of reasoning-by-analogy work, like Omohundro (2008). But the main thing I had in mind when making that comment, frankly, was the extensive literature on kings and empires. In broader biology, many genomes/organisms (bacteria, plants, etc) will also tend to expand to consume all available resources, if you put them in an environment where they can, e.g. without balancing predators.
I really like the report, although maybe I'm not a neutral judge, since I was already inclined to agree with pretty much everything you wrote. :-P
My own little AGI doom scenario is very much in the same mold, just more specific on the technical side. And much less careful and thorough all around. :)
For benefits of generality (4.3.2.1), an argument I find compelling is that if you're trying to invent a new invention or design a new system, you need a cross-domain system-level understanding of what you're trying to do and how. Like at my last job, it was not at all unusual for me to find myself sketching out the algorithms on a project and sketching out the link budget and scrutinizing laser spec sheets and scrutinizing FPGA spec sheets and nailing down end-user requirements, etc. etc. Not because I’m individually the best person at each of those tasks—or even very good!—but because sometimes a laser-related problem is best solved by switching to a different algorithm, or an FPGA-related problem is best solved by recognizing that the real end-user requirements are not quite what we thought, etc. etc. And that kind of design work is awfully hard unless a giant heap of relevant information and knowledge is all together in a single brain / world-model.
By “power” I mean something like: the type of thing that helps a wide variety of agents pursue a wide variety of objectives in a given environment. For a more formal definition, see Turner et al (2020).
I think the draft tends to use the term power to point to an intuitive concept of power/influence (the thing that we expect a random agent to seek due to the instrumental convergence thesis). But I think the definition above (or at least the version in the cited paper) points to a different concept, because a random agent has a single objective (rather than an intrinsic goal of getting to a state that would be advantageous for many different objectives). Here's a relevant passage by Rohin Shah from the Alignment Newsletter (AN #78) pertaining to that definition of power:
You might think that optimal agents would provably seek out states with high power. However, this is not true. Consider a decision faced by high school students: should they take a gap year, or go directly to college? Let’s assume college is necessary for (100-ε)% of careers, but if you take a gap year, you could focus on the other ε% of careers or decide to go to college after the year. Then in the limit of farsightedness, taking a gap year leads to a more powerful state, since you can still achieve all of the careers, albeit slightly less efficiently for the college careers. However, if you know which career you want, then it is (100-ε)% likely that you go to college, so going to college is very strongly instrumentally convergent even though taking a gap year leads to a more powerful state.
[EDIT: I should note that I didn't understand the cited paper as originally published (my interpretation of the definition is based on an earlier version of this post). The first author has noted that the paper has been dramatically rewritten to the point of being a different paper, and I haven't gone over the new version yet, so my comment might not be relevant to it.]
I think the draft tends to use the term power to point to an intuitive concept of power/influence (the thing that we expect a random agent to seek due to the instrumental convergence thesis). But I think the definition above (or at least the version in the cited paper) points to a different concept, because a random agent has a single objective (rather than an intrinsic goal of getting to a state that would be advantageous for many different objectives)
This is indeed a misunderstanding. My paper analyzes the single-objective setting; no intrinsic power-seeking drive is assumed.
I probably should have written the "because ..." part better. I was trying to point at the same thing Rohin pointed at in the quoted text.
Taking a quick look at the current version of the paper, my point still seems to me relevant. For example, in the environment in figure 16, with a discount rate of ~1, the maximally POWER-seeking behavior is to always stay in the same first state (as noted in the paper), from which all the states are reachable. This is analogous to the student from Rohin's example who takes a gap year instead of going to college.
A person does not become less powerful (in the intuitive sense) right after paying college tuition (or right after getting a vaccine) due to losing the ability to choose whether to do so. [EDIT: generally, assuming they make their choices wisely.]
I think POWER may match the intuitive concept when defined over certain (perhaps very complicated) reward distributions; rather than reward distributions that are IID-over-states (which is what the paper deals with).
Actually, in a complicated MDP environment—analogous to the real world—in which every sequence of actions results in a different state (i.e. the graph of states is a tree with a constant branching factor), the POWER of all the states that the agent can get to in a given time step is equal; when POWER is defined over an IID-over-states reward distribution.
Two clarifications. First, even in the existing version, POWER can be defined for any bounded reward function distribution - not just IID ones. Second, the power-seeking results no longer require IID. Most reward function distributions incentivize POWER-seeking, both in the formal sense, and in the qualitative "keeping options open" sense.
To address your main point, though, I think we'll need to get more concrete. Let's represent the situation with a state diagram.
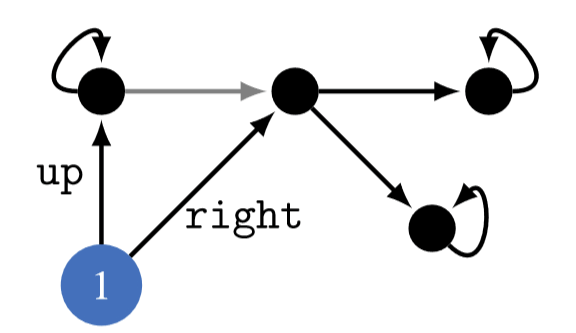
up is gap year, and right is go to college right away.Both you and Rohin are glossing over several relevant considerations, which might be driving misunderstanding. For one:
Power depends on your time preferences. If your discount rate is very close to 1 and you irreversibly close off your ability to pursue percent of careers, then yes, you have decreased your POWER by going to college right away. If your discount rate is closer to 0, then college lets you pursue more careers quickly, increasing your POWER for most reward function distributions.
You shouldn't need to contort the distribution used by POWER to get reasonable outputs. Just be careful that we're talking about the same time preferences. (I can actually prove that in a wide range of situations, the POWER of state 1 vs the POWER of state 2 is ordinally robust to choice of distribution. I'll explain that in a future post, though.)
My position on "is POWER a good proxy for intuitive-power?" is that yes, it's very good, after thinking about it for many hours (and after accounting for sub-optimality; see the last part of appendix B). I think the overhauled power-seeking post should help, but perhaps I have more explaining to do.
Also, I perceive an undercurrent of "goal-driven agents should tend to seek power in all kinds of situations; your formalism suggests they don't; therefore, your formalism is bad", which is wrong because the premise is false. (Maybe this isn't your position or argument, but I figured I'd mention it in case you believe that)
Actually, in a complicated MDP environment—analogous to the real world—in which every sequence of actions results in a different state (i.e. the graph of states is a tree with a constant branching factor), the POWER of all the states that the agent can get to in a given time step is equal; when POWER is defined over an IID-over-states reward distribution.
This is superficially correct, but we have to be careful because
- the theorems don't deal with the partially observable case,
- this implies an infinite state space (not accounted for by the theorems),
- a more complete analysis would account for facts like the probable featurization of the environment. For the real world case, we'd probably want to consider a planning agent's world model as featurizing over some set of learned concepts, in which case the intuitive interpretation should come back again. See also how John Wentworth's abstraction agenda may tie in with this work.
- different featurizations and agent rationalities would change the sub-optimal POWER computation (see the last 'B' appendix of the current paper), since it's easier to come up with good plans in certain situations than in others.
- The theorems now apply to the fully general, non-IID case. (not publicly available yet)
Basically, satisfactory formal analysis of this kind of situation is more involved than you make it seem.
You shouldn't need to contort the distribution used by POWER to get reasonable outputs.
I think using a well-chosen reward distribution is necessary, otherwise POWER depends on arbitrary choices in the design of the MDP's state graph. E.g. suppose the student in the above example writes about every action they take in a blog that no one reads, and we choose to include the content of the blog as part of the MDP state. This arbitrary choice effectively unrolls the state graph into a tree with a constant branching factor (+ self-loops in the terminal states) and we get that the POWER of all the states is equal.
This is superficially correct, but we have to be careful because
- the theorems don't deal with the partially observable case,
- this implies an infinite state space (not accounted for by the theorems),
The "complicated MDP environment" argument does not need partial observability or an infinite state space; it works for any MDP where the state graph is a finite tree with a constant branching factor. (If the theorems require infinite horizon, add self-loops to the terminal states.)
I think using a well-chosen reward distribution is necessary, otherwise POWER depends on arbitrary choices in the design of the MDP's state graph. E.g. suppose the student in the above example writes about every action they take in a blog that no one reads, and we choose to include the content of the blog as part of the MDP state. This arbitrary choice effectively unrolls the state graph into a tree with a constant branching factor (+ self-loops in the terminal states) and we get that the POWER of all the states is equal.
I replied to this point with a short post.
This arbitrary choice effectively unrolls the state graph into a tree with a constant branching factor (+ self-loops in the terminal states) and we get that the POWER of all the states is equal.
Not necessarily true - you're still considering the IID case.
I think using a well-chosen reward distribution is necessary, otherwise POWER depends on arbitrary choices in the design of the MDP's state graph. E.g. suppose the student in the above example writes about every action they take in a blog that no one reads, and we choose to include the content of the blog as part of the MDP state.
Yes, if you insist in making really weird modelling choices (and pretending the graph still well-models the original situation, even though it doesn't), you can make POWER say weird things. But again, I can prove that up to a large range of perturbation, most distributions will agree that some obvious states have more POWER than other obvious states.
Your original claim was that POWER isn't a good formalization of intuitive-power/influence. You seem to be arguing that because there exists a situation "modelled" by an adversarially chosen environment grounding such that POWER returns "counterintuitive" outputs (are they really counterintuitive, given the information available to the formalism?), therefore POWER is inappropriately sensitive to the reward function distribution. Therefore, it's not a good formalization of intuitive-power.
I deny both of the 'therefores.'
The right thing to do is just note that there is some dependence on modelling choices, which is another consideration to weigh (especially as we move towards more sophisticated application of the theorems to e.g. distributions over mesa objectives and their attendant world models). But you should sure that the POWER-seeking conclusions hold under plausible modelling choices, and not just the specific one you might have in mind. I think that my theorems show that they do in many reasonable situations (this is a bit argumentatively unfair of me, since the theorems aren't public yet, but I'm happy to give you access).
If this doesn't resolve your concern and you want to talk more about this, I'd appreciate taking this to video, since I feel like we may be talking past each other.
EDIT: Removed a distracting analogy.
Just to summarize my current view: For MDP problems in which the state representation is very complex, and different action sequences always yield different states, POWER-defined-over-an-IID-reward-distribution is equal for all states, and thus does not match the intuitive concept of power.
At some level of complexity such problems become relevant (when dealing with problems with real-world-like environments). These are not just problems that show up when one adverserially constructs an MDP problem to game POWER, or when one makes "really weird modelling choices". Consider a real-world inspired MDP problem where a state specifies the location of every atom. What makes POWER-defined-over-IID problematic in such an environment is the sheer complexity of the state, which makes it so that different action sequences always yield different states. It's not "weird modeling decisions" causing the problem.
I also (now) think that for some MDP problems (including many grid-world problems), POWER-defined-over-IID may indeed match the intuitive concept of power well, and that publications about such problems (and theorems about POWER-defined-over-IID) may be very useful for the field. Also, I see that the abstract of the paper no longer makes the claim "We prove that, with respect to a wide class of reward function distributions, optimal policies tend to seek power over the environment", which is great (I was concerned about that claim).
I’ve written a draft report evaluating a version of the overall case for existential risk from misaligned AI, and taking an initial stab at quantifying the risk from this version of the threat. I’ve made the draft viewable as a public google doc here (Edit: arXiv version here, video presentation here, human-narrated audio version here). Feedback would be welcome.
This work is part of Open Philanthropy’s “Worldview Investigations” project. However, the draft reflects my personal (rough, unstable) views, not the “institutional views” of Open Philanthropy.