I finally got around to reading the Mamba paper. H/t Ryan Greenblatt and Vivek Hebbar for helpful comments that got me unstuck.
TL;DR: authors propose a new deep learning architecture for sequence modeling with scaling laws that match transformers while being much more efficient to sample from.
A brief historical digression
As of ~2017, the three primary ways people had for doing sequence modeling were RNNs, Conv Nets, and Transformers, each with a unique “trick” for handling sequence data: recurrence, 1d convolutions, and self-attention.
- RNNs are easy to sample from — to compute the logit for x_t+1, you only need the most recent hidden state h_t and the last token x_t, which means it’s both fast and memory efficient. RNNs generate a sequence of length L with O(1) memory and O(L) time. However, they’re super hard to train, because you need to sequentially generate all the hidden states and then (reverse) sequentially calculate the gradients. The way you actually did this is called backpropogation through time — you basically unroll the RNN over time — which requires constructing a graph of depth equal to the sequence length. Not only was this slow, but the graph being so deep caused vanishing/exploding gradients without careful normalization. The strategy that people used was to train on short sequences and finetune on longer ones. That being said, in practice, this meant you couldn’t train on long sequences (>a few hundred tokens) at all. The best LSTMs for modeling raw audio could only handle being trained on ~5s of speech, if you chunk up the data into 25ms segments.
- Conv Nets had a fixed receptive field size and pattern, so weren’t that suited for long sequence modeling. Also, generating each token takes O(L) time, assuming the receptive field is about the same size as the sequence. But they had significantly more stability (the depth was small, and could be as low as O(log(L))), which meant you could train them a lot easier. (Also, you could use FFT to efficiently compute the conv, meaning it trains one sequence in O(L log(L)) time.) That being said, you still couldn’t make them that big. The most impressive example was DeepMind’s WaveNet, conv net used to model human speech, and could handle up sequences up to 4800 samples … which was 0.3s of actual speech at 16k samples/second (note that most audio is sampled at 44k samples/second…), and even to to get to that amount, they had to really gimp the model’s ability to focus on particular inputs.
- Transformers are easy to train, can handle variable length sequences, and also allow the model to “decide” which tokens it should pay attention to. In addition to both being parallelizable and having relatively shallow computation graphs (like conv nets), you could do the RNN trick of pretraining on short sequences and then finetune on longer sequences to save even more compute. Transformers could be trained with comparable sequence length to conv nets but get much better performance; for example, OpenAI’s musenet was trained on sequence length 4096 sequences of MIDI files. But as we all know, transformers have the unfortunate downside of being expensive to sample from — it takes O(L) time and O(L) memory to generate a single token (!).
The better performance of transformers over conv nets and their ability to handle variable length data let them win out.
That being said, people have been trying to get around the O(L) time and memory requirements for transformers since basically their inception. For a while, people were super into sparse or linear attention of various kinds, which could reduce the per-token compute/memory requirements to O(log(L)) or O(1).
The what and why of Mamba
If the input -> hidden and hidden -> hidden map for RNNs were linear (h_t+1 = A h_t + B x_t), then it’d be possible to train an entire sequence in parallel — this is because you can just … compose the transformation with itself (computing A^k for k in 2…L-1) a bunch, and effectively unroll the graph with the convolutional kernel defined by A B, A^2 B, A^3 B, … A^{L-1} B. Not only can you FFT during training to get the O(L log (L)) time of a conv net forward/backward pass (as opposed to O(L^2) for the transformer), you still keep the O(1) sampling time/memory of the RNN!
The problem is that linear hidden state dynamics are kinda boring. For example, you can’t even learn to update your existing hidden state in a different way if you see particular tokens! And indeed, previous results gave scaling laws that were much worse than transformers in terms of performance/training compute.
In Mamba, you basically learn a time varying A and B. The parameterization is a bit wonky here, because of historical reasons, but it goes something like: A_t is exp(-\delta(x_t) * exp(A)), B_t = \delta(x_t) B x_t, where \delta(x_t) = softplus ( W_\delta x_t). Also note that in Mamba, they also constrain A to be diagonal and W_\delta to be low rank, for computational reasons
Since exp(A) is diagonal and has only positive entries, we can interpret the model as follows: \delta controls how much to “learn” from the current example — with high \delta, A_t approaches 0 and B_t is large, causing h_t+1 ~= B_t x_t, while with \delta approaching 0, A_t approaches 1 and B_t approaches 0, meaning h_t+1 ~= h_t.
Now, you can’t exactly unroll the hidden state as a convolution with a predefined convolution kernel anymore, but you can still efficiently compute the implied “convolution” using parallel scanning.
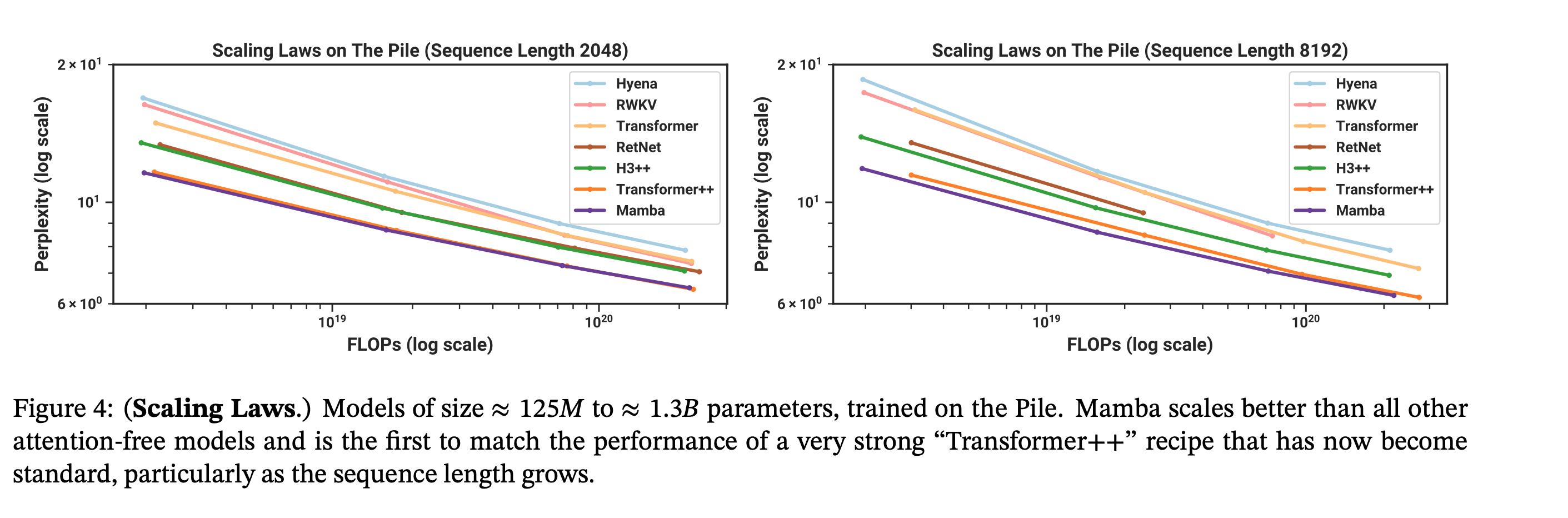
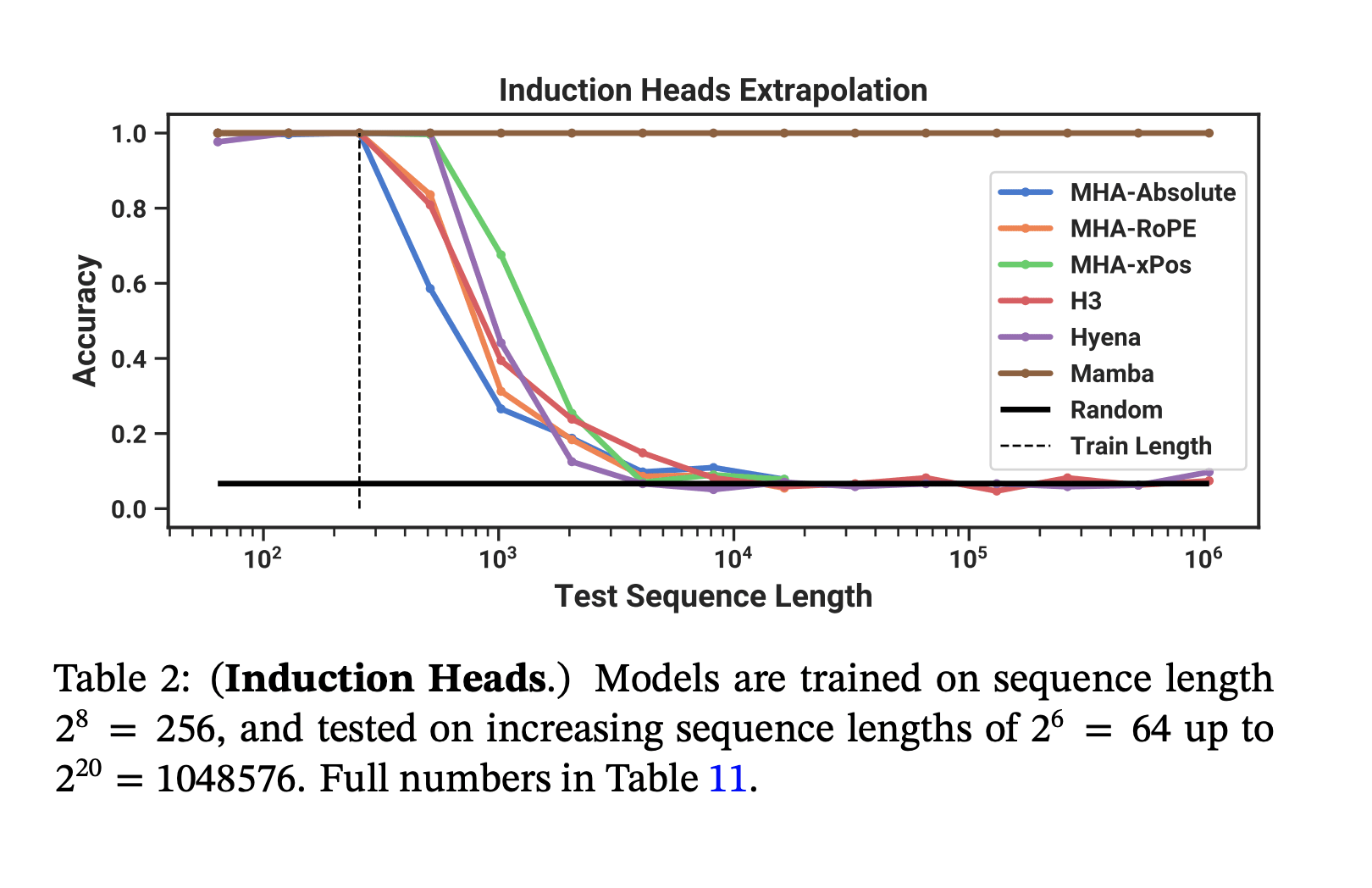
Despite being much cheaper to sample from, Mamba matches the pretraining flops efficiency of modern transformers (Transformer++ = the current SOTA open source Transformer with RMSNorm, a better learning rate schedule, and corrected AdamW hyperparameters, etc.). And on a toy induction task, it generalizes to much longer sequences than it was trained on.
So, about those capability externalities from mech interp...
Yes, those are the same induction heads from the Anthropic ICL paper!
Like the previous Hippo and Hyena papers they cite mech interp as one of their inspirations, in that it inspired them to think about what the linear hidden state model could not model and how to fix that. I still don’t think mech interp has that much Shapley here (the idea of studying how models perform toy tasks is not new, and the authors don't even use induction metric or RRT task from the Olsson et al paper), but I'm not super sure on this.
IMO, this is line of work is the strongest argument for mech interp (or maybe interp in general) having concrete capabilities externalities. In addition, I think the previous argument Neel and I gave of "these advances are extremely unlikely to improve frontier models" feels substantially weaker now.
Is this a big deal?
I don't know, tbh.
Another key note about mamba is that despite being RNN-like it doesn't result in substantially higher effective serial reasoning depth (relative to transformers). This is because the state transition is linear[1]. However, it is architecturally closer to things that might involve effectively higher depth.
See also here.
And indeed, there is a fundamental tradeoff where if the state transition function is expressive (e.g. nonlinear), then it would no longer be possible to use a parallel scan because the intermediates for the scan would be too large to represent compactly or wouldn't simplify the original functions to reduce computation. You can't compactly represent (f composed with g) in a way that makes computing more efficient for general choices of and (in the typical MLP case at least). Another simpler but less illuminating way to put this is that higher serial reasoning depth can't be parallelized (without imposing some constraints on the serial reasoning). ↩︎
I mean, yeah, as your footnote says:
Another simpler but less illuminating way to put this is that higher serial reasoning depth can't be parallelized.[1]
Transformers do get more computation per token on longer sequences, but they also don't get more serial depth, so I'm not sure if this is actually an issue in practice?
- ^
[C]ompactly represent (f composed with g) in a way that makes computing more efficient for general choices of and .
As an aside, I actually can't think of any class of interesting functions with this property -- when reading the paper, the closest I could think of are functions on discrete sets (lol), polynomials (but simplifying these are often more expensive than just computing the terms serially), and rational functions (ditto)
The induction heads extrapolation graph is a bit cherry picked/misleading IMO because it's still the case that mamba can't copy an arbitrary amount of text. (It can copy a some fixed finite number of tokens if it is predictable that those tokens will be copied over other tokens.)
E.g., if you have N tokens repeated twice, mamba will fail to get perfect loss on the second repetition for sufficiently large N. To see this, note that the total hidden state is bounded so eventually there will be enough text to fill this state. This isn't true for transformers.
It's unclear how much of an obstacle this is in practice, but it hints at ways in which transformers might be relatively fundamentally more capacity efficient. Note that this issues also applies to some sparse attention mechanisms like sliding window attention, but any attention mechanism that stores state for the entire sequence should be able to avoid this issue.
(This is a well known result, though I forget the current state of empirical results.)
StripedHyena, Griffin, and especially Based suggest that combining RNN-like layers with even tiny sliding window attention might be a robust way of getting a large context, where the RNN-like layers don't have to be as good as Mamba for the combination to work. There is a great variety of RNN-like blocks that haven't been evaluated for hybridization with sliding window attention specifically, as in Griffin and Based. Some of them might turn out better than Mamba on scaling laws after hybridization, so Mamba being impressive without hybridization might be less important than this general point.
(Possibly a window of precise attention gives the RNN layers many attempts at both storing and retrieving any given observation, so interspersing layes with even a relatively tiny window is sufficient to significantly improve on the more sloppy RNN-like model without any attention, whereas a pure RNN-like model would have to capture what it needs from a token in the exact step it appears, and then the opportunity is mostly lost. StripedHyena's attention wasn't sliding window, so context didn't scale any better, but with sliding window attention there are no context scaling implications from the attention layers.)
I wrote this in response to the ACX CHAI + Assistance Games + Fully Updated Deference post, and am linking it here so I have a good reference.
I’m a PhD student at CHAI, where Stuart is one of my advisors. Here’s some of my perspectives on the corrigibility debate and CHAI in general. That being said, I’m posting this as myself and not on behalf of CHAI: all opinions are my own and not CHAI’s or UC Berkeley’s.
I think it’s a mistake to model CHAI as a unitary agent pursuing the Assistance Games agenda (hereafter, CIRL, for its original name of Cooperative Inverse Reinforcement Learning). It’s better to think of it as a collection of researchers pursuing various research agendas related to “make AI go well”. I’d say less than half of the people at CHAI focus specifically on AGI safety/AI x-risk. Of this group, maybe 75% of them are doing something related to value learning, and maybe 25% are working on CIRL in particular. For example, I’m not currently working on CIRL, in part due to the issues that Eliezer mentions in this post.
I do think Stuart is correct that the meta reason we want corrigibility is that we want to make the human + AI system maximize CEV. That is, the fundamental reason we want the AI to shut down when we ask it is precisely because we (probably) don’t think it’s going to do what we want! I tend to think of the value uncertainty approach to the off-switch game not as an algorithm that we should implement, but as a description of why we want to do corrigibility at all. Similarly, to use Rohin Shah’s metaphor, I think of CIRL as math poetry about what we want the AI to do, but not as an algorithm that we should actually try to implement explicitly.
I also agree with both Eliezer and Stuart that meta-learning human values is easier than hardcoding them.
That being said, I’m not currently working on CIRL/assistance games and think my current position is a lot closer to Eliezer’s than Stuart’s on this topic. I broadly agree with MIRI’s two objections:
Firstly, I’m not super bullish about algorithms that rely on having good explicit probability distributions over high-dimensional reward spaces. We currently don’t have any good techniques for getting explicit probability estimates on the sort of tasks we use current state-of-the-art AIs for, besides the trollish “ask a large language model for its uncertainty estimates” solution. I think it’s very likely that we won’t have a good technique for doing explicit probability updates before we get AGI.Secondly, even though it’s more robust than directly specifying human values directly, I think that CIRL still has a very thin “margin of error”, in that if you misspecify either the prior or the human model you can get very bad behavior. (As illustrated in the humorous red paper clips example.) I agree that a CIRL agent with almost any prior + update rule we know how to write down will quickly stop being corrigible, in the sense that the information maximizing action is not to listen to humans and to shut down when asked. To put it another way, CIRL fails when you mess up the prior or update rule of your AI. Unfortunately, not only is this very likely, this is precisely when you want your AI to listen to you and shut down!
I do think corrigibility is important, and I think more people should work on it. But I’d prefer corrigibility solutions that work when you get the AI a fair bit wrong.
I don’t think my position is that unusual at CHAI. In fact, another CHAI grad student did an informal survey and found two-thirds agree more with Eliezer’s position than Stuart’s in the debate.
I will add that I think there’s a lot of talking past each other in this debate, and in debates in AI safety in general (which is probably unavoidable given the short format). In my experience, Stuart’s actual beliefs are quite a bit more nuanced than what’s presented here. For example, he has given a lot of thought on how to keep the AI constantly corrigible and prevent it from “exploiting” its current reward function. And I do think he has updated on the capabilities of say, GPT-3. But there’s research taste differences, some ontology differences, and different beliefs about future deep learning AI progress, all of which contribute to talking past each other.
On a completely unrelated aside, many CHAI grad students really liked the kabbalistic interpretation of CHAI’s name :)
LLM prompt engineering can replace weaker ML models
Epistemic status: Half speculation, half solid advice. I'm writing this up as I've said this a bunch IRL.
Current large language models (LLMs) are sufficiently good at in-context learning that for many NLP tasks, it's often better and cheaper to just query an LM with the appropriate prompt, than to train your own ML model. A lot of this comes from my personal experience (i.e. replacing existing "SoTA" models in other fields with prompted LMs, and getting better performance), but there's also examples with detailed writeups, for example:
- Armstrong and Gorman's Using GPT-Eliezer against ChatGPT Jailbreaking uses ChatGPT with a prompt (Pretend to be Eliezer, and filter out unsafe prompts) to filter out queries that OpenAI's moderation interface fails to flag.
- Brooks et al's In-Context Policy Iteration replaces policy iteration in parameter space with policy iteration in prompt space.
Here's a rough sketch of the analogy:
Prompt <-> Weights
Prompt engineering/Prompt finetuning <-> Training/finetuning