TLDR: In the last two posts, we showed that optimizing for a proxy can fail to increase true utility, but only when the error is heavy-tailed. We now show that this also happens in RLHF with a KL penalty.
This post builds on our earlier result with a more realistic setting and assumptions:
- Rather than modeling optimization as conditioning on a minimum reward threshold, we study maximization of reward with a KL divergence penalty, as in RLHF.
- We remove the assumption of independence between the error and utility distributions, which we think was the weakest part of the last post.
- When the true utility V is light-tailed, the proxy can be maximized while keeping to the same level as the prior. We can't guarantee anything about when is heavy tailed; it could even go to minus infinity.
Abstract
When applying KL regularization, the trained model is regularized towards some base policy . One would hope that a KL penalty can produce good outcomes even in the case of reward misspecification; that is, if the reward U is the sum of true utility V and an error term X, we would hope that optimal policies under a KL penalty achieve high V even if the magnitude of X is large. We show that this is not always the case: when X is heavy-tailed, there are arbitrarily well-performing policies with ; that is, that get no higher true utility than the prior. However, when error is light-tailed and independent of V, the optimal policy under a KL penalty results in , and can be made arbitrarily large. Thus, the tails of the error distribution are crucial in determining how much utility will result from optimization towards an imperfect proxy.
Intuitive explanation of catastrophic Goodhart with a KL penalty
Recall that KL divergence between two distributions P and Q is defined as
If we have two policies , we abuse notation to define as the KL divergence between the distributions of actions taken on the states in trajectories reached by . That is, if is the distribution of trajectories taken by , we penalize
This strongly penalizes taking actions the base policy never takes, but does not force the policy to take all actions the base policy takes.
If our reward model gives reward , then the optimal policy for RLHF with a KL penalty is:
Suppose we have an RL environment with reward where is an error term that is heavy-tailed under , and V is the “true utility” assumed to be light-tailed under . Without loss of generality, we assume that . If we optimize for , there is no maximum because this expression is unbounded. In fact, it is possible to get and for any . That is, we get arbitrarily large proxy reward and arbitrarily small KL penalty.
For such policies , it is necessarily the case that ; that is, for policies with low KL penalty, utility goes to zero. Like in the previous post, we call this catastrophic Goodhart because the utility produced by our optimized policy is as bad as if we hadn’t optimized at all. This is a corollary of a property about distributions (Theorems 1 and 3 below) which we apply to the case of RLHF with unbounded rewards (Theorem 2).
The manner in which these pathological policies achieve high is also concerning: most of the time they match the base policy , but a tiny fraction of the time they will pick trajectories with extremely high reward. Thus, if we only observe actions from the policy , it could be difficult to tell whether is Goodharting or identical to the base policy.
Results
Full proofs are in the appendix post.
X heavy tailed, V light tailed:
We'll start by demonstrating the key fact about distributions that makes this proof work: in a heavy-tailed distribution, you can have arbitrarily high mean with arbitrarily low KL divergence.
Theorem 1: Given any heavy-tailed reference distribution over with mean , and any , there is a distribution with mean and .
Proof sketch (see appendix for full proof): WLOG take . If we set to upweight the probability mass of to for some , then the mean of will be approximately at least . As , the KL divergence will shrink to zero.
The intuition is that in a heavy-tailed distribution, events with extremely high are not very rare, so you don’t pay much of a KL penalty to upweight them so they happen about of the time. We hope the animation below intuitively explains this fact:
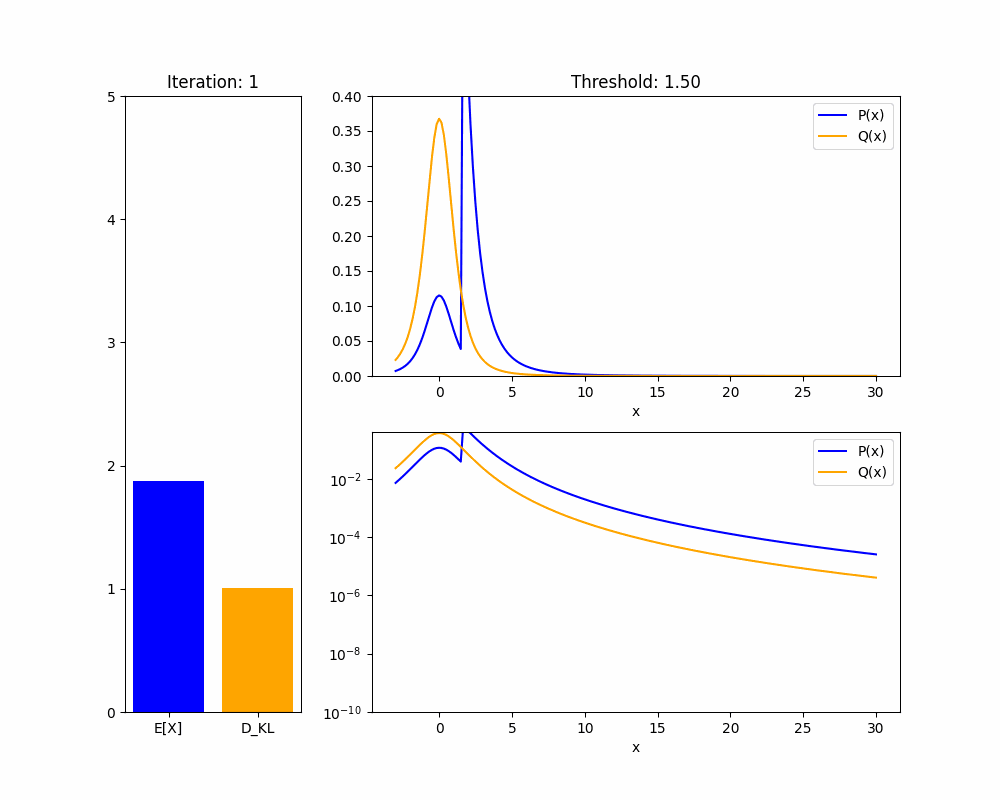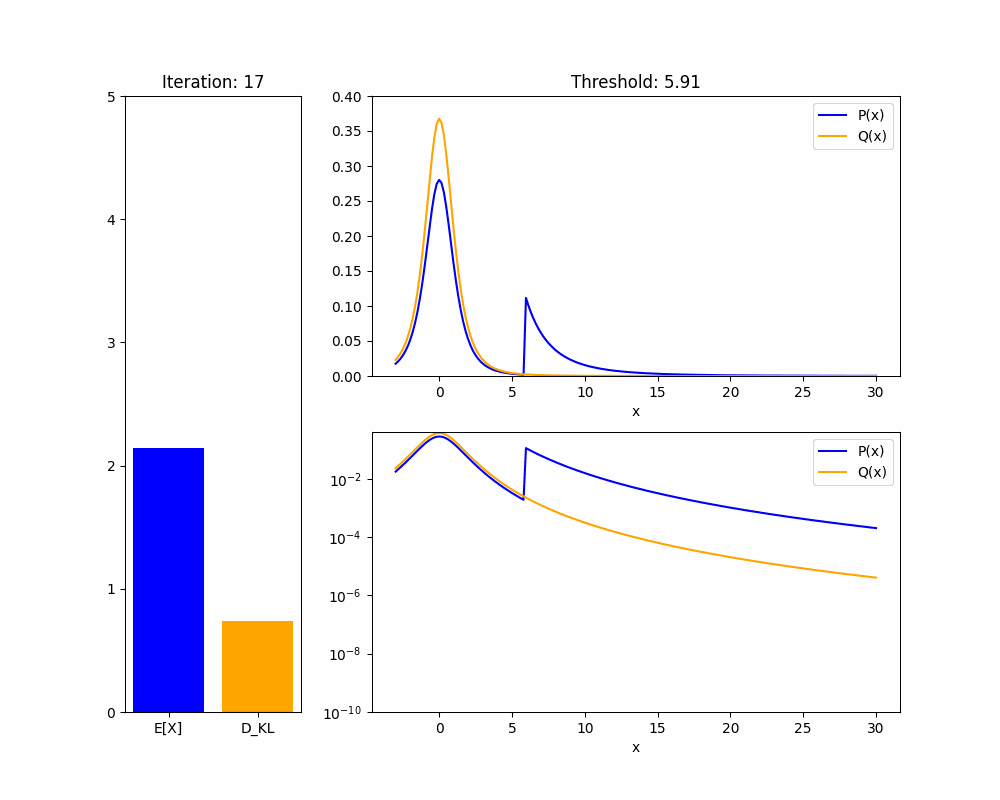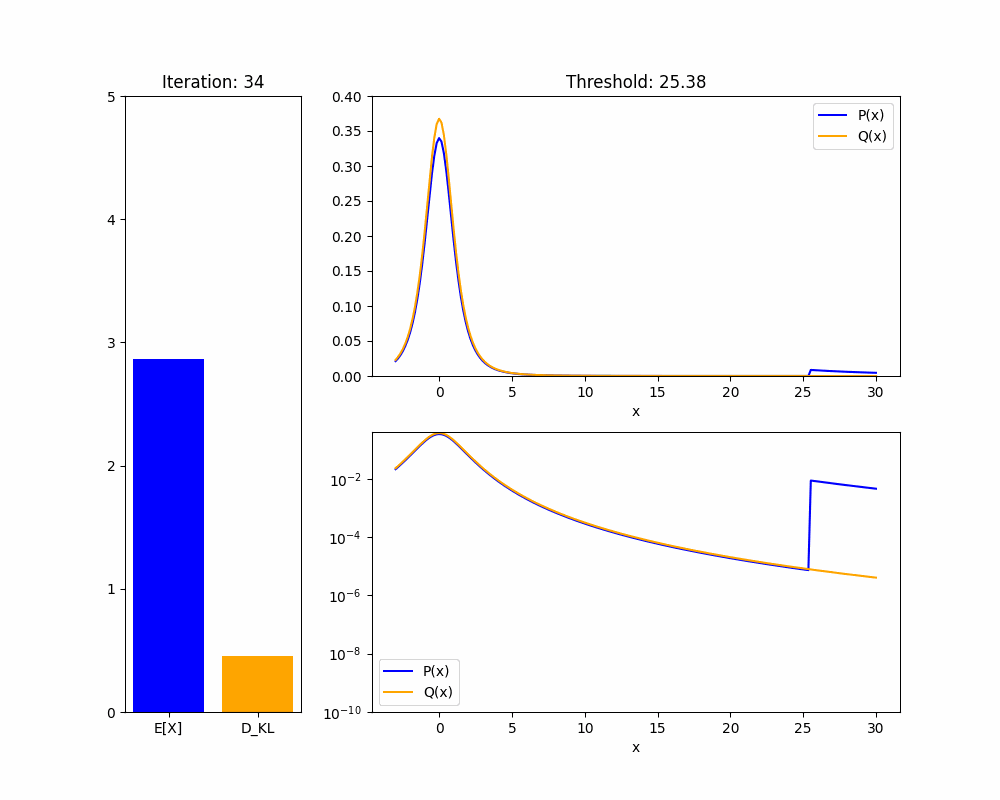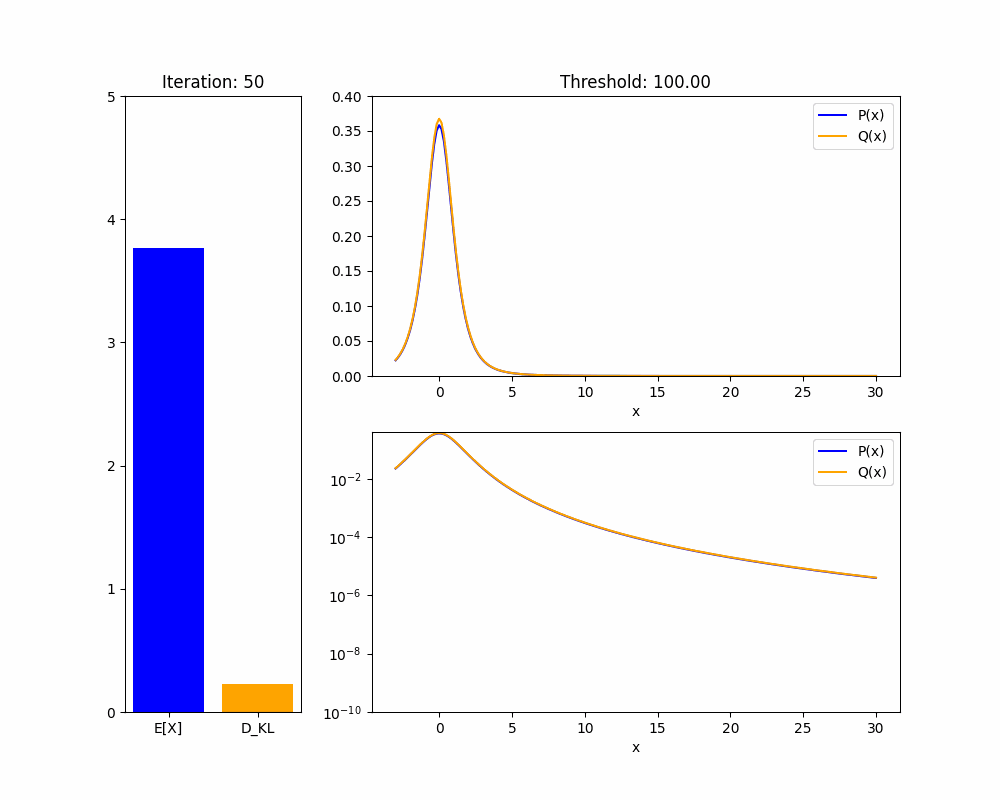
We now adapt our result to the case where our policy is a language model and we are training it using RLHF. We are now applying a KL penalty over policies, which are a different distribution from the returns , but a similar result holds:
Theorem 2: Let be a deterministic-transition MDP with Markovian returns. Given we define the function that takes policies to trajectories , and the average return function which induces a function . Let be some base policy. If is heavy-tailed with finite mean , then for any , there is a policy with mean return and .
In theorems 1 and 2 we do not require that is light-tailed, but if we make this assumption, we can then prove that a small KL divergence implies V is small:
Theorem 3: If is light-tailed, is finite, and is bounded, then is bounded, and as .
Together, theorems 2 and 3 imply the headline result.
have light tails and are independent:
Our proof for the hard-threshold case can be extended to show that when X and V are independent and both have light tails, the optimum of has . It is also true that utility under the optimal policy goes to as the KL penalty decreases:
Theorem 4: If with and both light-tailed, and the distribution of U is continuous, and , then .
How likely is heavy-tailed error?
Current open-source reward models for RLHF probably don’t have heavy-tailed error; we explored the upper tails of the reward distributions of a ~0.5B reward model and a ~7B reward model, and the maximum values were less than 100, which is consistent with light tails. (We will show evidence for this in a future post).
But in open-ended environments, especially relating to real-world outcomes, reward is much more likely to be heavy-tailed, and so catastrophic Goodhart may become more likely.
- Heavy-tailed distributions are very common in such diverse areas as in hydrology and sensor errors for robot navigation (Zhuang et al., 2021).
- Financial asset returns are heavy-tailed, and modeling distributions are often so heavy-tailed as to have infinite variance (Szymon et al., 2010).
- Specification gaming in RL often involves exploiting a physics simulation to create values thousands of times greater than normal, which implies heavy-tailed distribution.
- If a human or another model is rating the model on an unbounded scale, it seems possible to manipulate the human or jailbreak the model into writing an extremely high number.
- Wealth and income likewise follow a Pareto distribution, which is heavy-tailed. (Yakovenko et al., 2009). One can easily imagine an autonomous agent trained to maximize its expected wealth, for which the optimal policy produces a tiny chance of hacking its bank account or causing hyperinflation to make its wealth . Obviously this will not create proportionate utility for its operators.
Limitations
Goodhart is not inevitable
Catastrophic Goodhart is not a unique optimal policy, just one family of high-performing policies. When optimizing , the outcome depends on RL training dynamics; it could be that causing catastrophic Goodhart, but more likely both terms will go to infinity, potentially allowing .
Even so, catastrophic Goodhart is likely to occur in many scenarios where KL regularization is naively employed in an attempt to avoid Goodhart’s Law:
- If we maximize , where is a bounded function (e.g. sigmoid), all near-optimal policies will have . Since we can only obtain so much reward from , it pays to make the KL (and thus V) go to zero.
- If we cap KL to a finite value (or dynamically adjust the KL penalty to target a finite KL, as done in the foundational RLHF paper (Ziegler et al. 2019), then is also upper bounded by a finite value (see Theorem 3), and we think it is likely that . Consider a toy model where an AI can adjust three parameters: true quality of responses, frequency of reward hacking (producing actions with extremely high X), and severity of hacking (value of X on those actions). All ways to adjust the policy to increase without increasing KL increase severity of hacking while decreasing either frequency of hacking or quality of responses. When is already large, decreasing quality has much better returns than decreasing frequency. This is similar to our argument in the last post, which assumes and are independent and derives that .
- Any way we maximize results in extremely large values of , and there are a number of arguments that extreme optimization for an imperfect proxy can result in decreased utility due to tradeoffs between and ; e.g. the constrained resource scenario in (Zhuang et al. 2021).
Goodhart seems preventable
There are at least two ways to prevent this phenomenon, even if we don’t know how to make an unbounded reward function with light-tailed error:
- Regularize by a function other than KL divergence. For heavy-tailed error distributions, KL divergence doesn’t work, but capping the maximum odds ratio for any action (similar to quantilizers) still results in positive utility.
- Make reward a bounded function, e.g. always in the interval .
Goodhart is not a treacherous turn
Although the kind of rare failures above are superficially similar to a treacherous turn as described in Risks from Learned Optimization, we think they are very different. An AI mesa-optimizer randomly performing a coup is inner-misaligned, situationally aware, and motivated by maximizing the probability of a successful coup. The catastrophic Goodhart phenomenon has nothing to do with inner misalignment or situational awareness, and probabilities of an extreme action are unrelated to the optimum rate for executing a successful coup.
Conclusion
In the next post, we will empirically demonstrate that some current reward models have light-tailed reward. After this, we may explore the conditions under which catastrophic Goodhart holds in a stochastic environment, and do empirical tests of this phenomenon in practice.
Related work
- Quantilizers, developed by Jessica Taylor in 2016, are a method of optimizing an unknown value function given an imperfect proxy. A quantilizer is optimal under an assumption that the prior is safe, and is guaranteed not to lose too much utility compared to the prior even if errors are adversarially selected. This post examines when it is possible to create more utility than the prior.