This is a more technical followup to the last post, putting precise bounds on when regressional Goodhart leads to failure or not. We'll first show conditions under which optimization for a proxy fails, and then some conditions under which it succeeds. (The second proof will be substantially easier.)
Related work
In addition to the related work sections of the previous post, this post makes reference to the textbook An Introduction to Heavy-Tailed and Subexponential Distributions, by Foss et al. Many similar results about random variables are present in the textbook, though we haven't seen this posts's results elsewhere in the literature before. We mostly adopt their notation here, and cite a few helpful lemmas.
Main result: Conditions for catastrophic Goodhart
Suppose that and are independent real-valued random variables. We're going to show, roughly, that if
- is subexponential (a slightly stronger property than being heavy-tailed).
- has lighter tails than by more than a linear factor, meaning that the ratio of the tails of and the tails of grows superlinearly.[1]
then .
Less formally, we're saying something like "if it requires relatively little selection pressure on to get more of and asymptotically more selection pressure on to get more of , then applying very strong optimization towards will not get you even a little bit of optimization towards - all the optimization power will go towards ."
Proof sketch and intuitions
The conditional expectation is given by ,[2] and we divide the integral in the numerator into 4 regions, showing that each region's effect on the conditional expectation of V is similar to that of the corresponding region in the unconditional expectation .
The regions are defined in terms of a slow-growing function such that the fiddly bounds on different pieces of the proof work out. Roughly, we want it to go to infinity so that is likely to be less than in the limit, but grow slowly enough that the shape of 's distribution within the interval doesn't change much after conditioning.
In the table below, we abbreviate the condition as .
| Region | Why its effect on is small | Explanation |
| is too low | In this region, and , both of which are unlikely. | |
| The tail distribution of X is too flat to change the shape of 's distribution within this region. | ||
| is low, and . | There are increasing returns to each bit of optimization for X, so it's unlikely that both X and V have moderate values.[3] | |
| is too low | X is heavier-tailed than V, so the condition that is much less likely than in . |
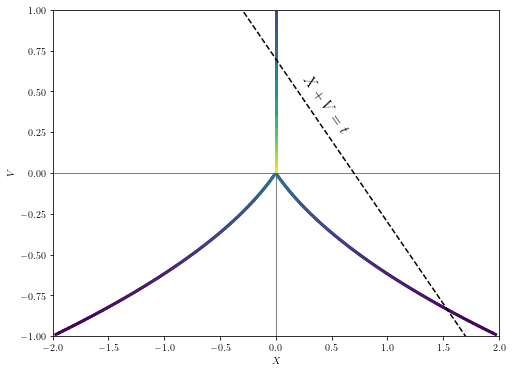
Here's a diagram showing the region boundaries at , , and in an example where and , along with a negative log plot of the relevant distribution:
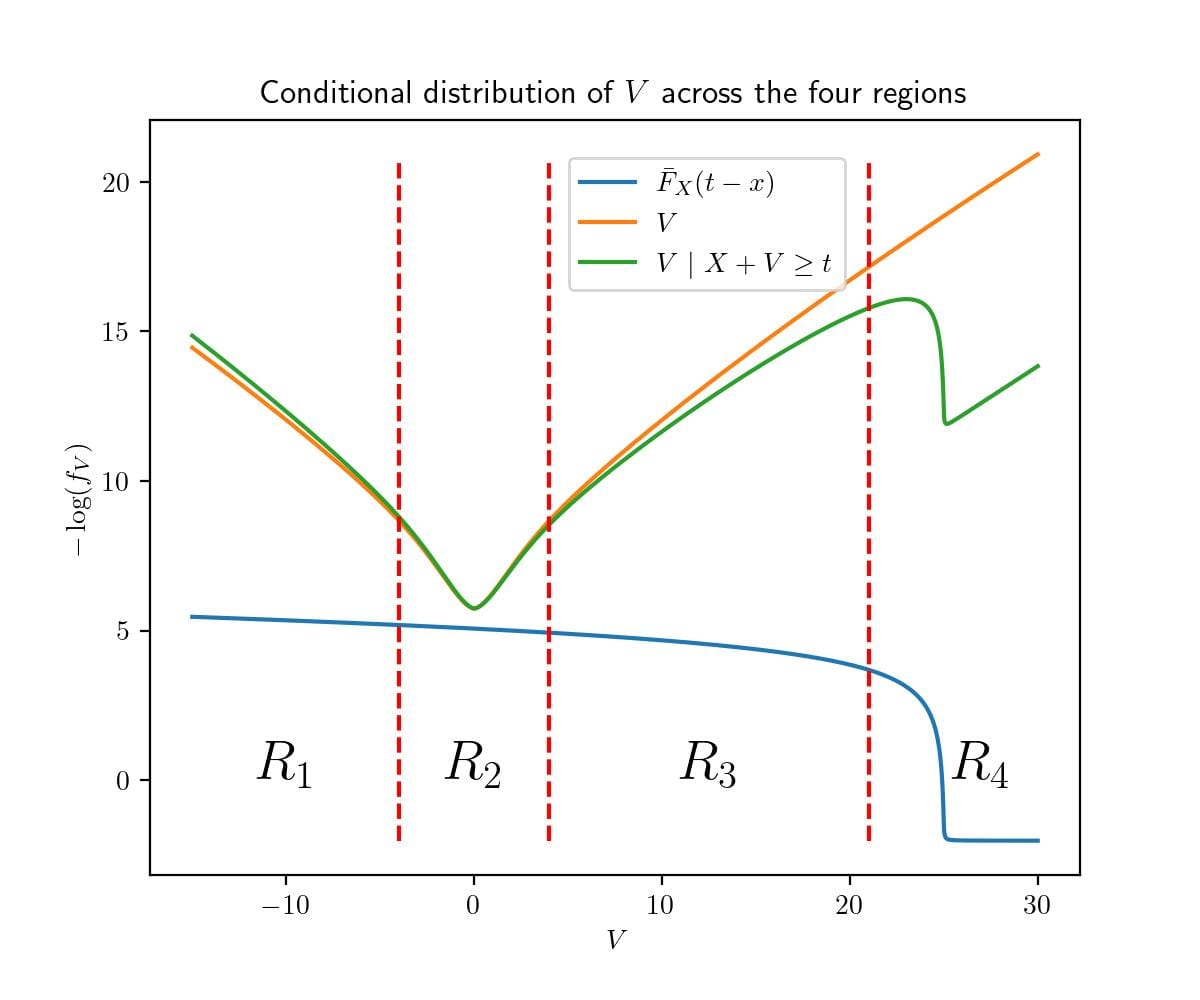
Note that up to a constant vertical shift of normalization, the green curve is the pointwise sum of the blue and orange curves.
Full proof
To be more precise, we're going to make the following definitions and assumptions:
- Let be the PDF of at the value . We assume for convenience that exists, is integrable, etc, though we suspect that this isn't necessary, and that one could work through a similar proof just referring to the tails of . We won't make this assumption for .
- Let and , similarly for and .
- Assume has a finite mean: converges absolutely.
- is subexponential.
- Formally, this means that .
- This happens roughly whenever has tails that are heavier than for any and is reasonably well-behaved; counterexamples to the claim "long-tailed implies subexponential" exist, but they're nontrivial to exhibit.
- Examples of subexponential distributions include log-normal distributions, anything that decays like a power law, the Pareto distribution, and distributions with tails asymptotic to for any .
- We require for that its tail function is substantially lighter than X's, namely that for some .[1]
- This implies that .
With all that out of the way, we can move on to the proof.
The unnormalized PDF of conditioned on is given by . Its expectation is given by .
Meanwhile, the unconditional expectation of V is given by .
We'd like to show that these two expectations are equal in the limit for large . To do this, we'll introduce . (More pedantically, this should really be , which we'll occasionally use where it's helpful to remember that this is a function of .)
For a given value of , is just a scaled version of , so the conditional expectation of is given by . But because , the numerator and denominator of this fraction are (for small ) close to the unconditional expectation and , respectively.
We'll aim to show that for all we have for sufficiently large that and , which implies (exercise) that the two expectations have limiting difference zero. But first we need some lemmas.
Lemmas
Lemma 1: There is depending on such that:
- (a)
- (b)
- (c)
- (d) .
Proof: Lemma 2.19 from Foss implies that if is long-tailed (which it is, because subexponential implies long-tailed), then there is such that condition (a) holds and is -insensitive; by Proposition 2.20 we can take such that for sufficiently large , implying condition (b). Conditions (c) and (d) follow from being -insensitive.
Lemma 2: Suppose that is whole-line subexponential and is chosen as in Lemma 1. Also suppose that . Then
Proof: This is a slight variation on lemma 3.8 from [1], and follows from the proof of Lemma 2.37. Lemma 2.37 states that
but it is actually proved that
If we let , then we get
where . Multiplying by , we have ,
and because as and , we can say that for some , . Therefore for sufficiently large t.
By Theorem 3.6, is , so the LHS is as desired.
Bounds on the numerator
We want to show, for arbitrary , that in the limit as . Since
it will suffice to show that the latter quantity is less than for large .
We're going to show that is small by showing that the integral gets arbitrarily small on each of four pieces: , , , and .
We'll handle these case by case (they'll get monotonically trickier).
Region 1:
Since is absolutely convergent, for sufficiently large we will have, since goes to infinity by Lemma 1(a).
Since is monotonically increasing and , we know that in this interval .
So we have
as desired.
Region 2:
By lemma 1(d), is such that for sufficiently large , on the interval . (Note that the value of this upper bound depends only on and , not on or .) So we have
.
Region 3:
For the third part, we'd like to show that . Since
it would suffice to show that the latter expression becomes less than for large , or equivalently that .
The LHS in this expression is the unconditional probability that and , but this event implies , and . So we can write
by Lemma 2.
Region 4:
For the fourth part, we'd like to show that for large .
Since , it would suffice to show . But note that since by Lemma 1(c), this is equivalent to , which (by Lemma 1(b)) is equivalent to .
Note that , so it will suffice to show that both terms in this sum are .
The first term is because we assumed for some .
For the second term, we have for the same reason.
This completes the bounds on the numerator.
Bounds on the denominator
For the denominator, we want to show that , so it'll suffice to show as .
Again, we'll break up this integral into pieces, though they'll be more straightforward than last time. We'll look at , , and .
- .
- But since goes to infinity, this left tail of the integral will contain less and less of 's probability mass over time.
- But by Lemma 1(d) we know that this goes to zero for large .
- .
- But for sufficiently large we have , so we obtain
by the results of the previous section.
- But for sufficiently large we have , so we obtain
This completes the proof!
Light tails imply
Conversely, here's a case where we do get arbitrarily high for large . This generalizes a consequence of the lemma from Appendix A of Scaling Laws for Reward Model Overoptimization (Gao et al., 2022), which shows this result in the case where is either bounded or normally distributed.
Suppose that satisfies the property that .[4] This implies that has tails that are dominated by for any , though it's a slightly stronger claim because it requires that not be too "jumpy" in the decay of its tails.[5]
We'll show that for any with a finite mean which has no upper bound, .
In particular we'll show that for any , .
Proof
Let , which exists by our assumption that is unbounded.
Let . (If this is undefined because the conditional has probability , we'll have the desired result anyway since then would always be at least .)
Observe that for all , (assuming it is defined), because we're conditioning on an event which is more likely for larger (since and are independent).
First, let's see that . This ratio of probabilities is equal to
which, by our assumption that , will get arbitrarily small as increases for any positive .
Now, consider . We can break this up as the sum across outcomes of for the three disjoint outcomes , , and . Note that we can lower bound these expectations by respectively. But then once is large enough that , this weighted sum of conditional expectations will add to more than (exercise).
Answers to exercises from last post
- Show that when and are independent and , . Conclude that . This means that given independence, optimization always produces a plan that is no worse than random.
Proof: Fixing a value of , we have for all that. Since the conditional expectation after seeing any particular value of is at least , this will be true when averaged across all proportional to their frequency in the distribution of . This means that for all , so the inequality also holds in the limit.
- When independence is violated, an optimized plan can be worse than random, even if your evaluator is unbiased. Construct a joint distribution for and such that , , and for any , but .
Solution: Suppose that is distributed with a PDF equal to , and the conditional distribution of is given by
where is a random variable that is equal to with 50/50 odds. The two-dimensional heatmap looks like this:
Now, conditioning on with , we have one of two outcomes: either , or and .
The first case has an unconditional probability of , and a conditional expectation of .
The second case has an unconditional probability of , and a conditional expectation of at most since all values of in the second case are at most that large.
So, abbreviating these two cases as and respectively, the overall conditional expectation is given by
as desired.
This sort of strategy works for any fixed distribution of , so long as the distribution is not bounded below and has finite mean; we can replace with some sufficiently fast-growing function to get a zero-mean conditional distribution that behaves the same.
For a followup exercise, construct an example of this behavior even when all conditional distributions have variance at most .
- ^
We actually just need , so we can have e.g. .
- ^
We'll generally omit and terms in the interests of compactness and laziness; the implied differentials should be pretty clear.
- ^
The diagrams in the previous post show visually that when and are both heavy-tailed and is large, most of the probability mass has , or vice versa.
- ^
This proof will actually go through if we just have for any constant , which is a slightly weaker condition (just replace with in the proof as necessary). For instance, could have probability of being equal to for , which would satisfy this condition for but not .
- ^
If has really jumpy tails, the limit of the mean of the conditional distribution may not exist. Exercise: what goes wrong when has a probability of being equal to for and is a standard normal distribution?