This is a two-part sequence of posts, in the ancient LessWrong tradition of decision-theory-posting. This first part will introduce various concepts of bargaining solutions and dividing gains from trade, which the reader may or may not already be familiar with.
The upcoming part will be about how all introduced concepts from this post are secretly just different facets of the same underlying notion, as originally discovered by John Harsanyi back in 1963 and rediscovered by me from a completely different direction. The fact that the various different solution concepts in cooperative game theory are all merely special cases of a General Bargaining Solution for arbitrary games, is, as far as I can tell, not common knowledge on Less Wrong.
Bargaining Games
Let's say there's a couple with a set of available restaurant options. Neither of them wants to go without the other, and if they fail to come to an agreement, the fallback is eating a cold canned soup dinner at home, the worst of all the options. However, they have different restaurant preferences. What's the fair way to split the gains from trade?
Well, it depends on their restaurant preferences, and preferences are typically encoded with utility functions. Since both sides agree that the disagreement outcome is the worst, they might as well index that as 0 utility, and their favorite respective restaurants as 1 utility, and denominate all the other options in terms of what probability mix between a cold canned dinner and their favorite restaurant would make them indifferent. If there's something that scores 0.9 utility for both, it's probably a pretty good pick!
Although, there's something off about setting up the problem like this. There's no term for intensity of preferences! Someone who cared very little about food would have their preferences rank just as strongly as someone who had strong restaurant opinions!
In a sense, there's three responses to this objection.
The first response is that we might be zooming in too hard on the restaurant bargaining game in particular. In a broader context, a person having weak restaurant preferences may just be another way of saying that they are quick to trade off their choice of restaurant to someone else in return for other things they might desire. And so, in the broader bargaining game of a relationship where more is at stake than this one-time choice of restaurant, things may be fair. But in the restaurant bargaining game in particular, things can look unfair for the losing party, when in fact they traded off "ability to determine restaurant" in exchange for more concessions elsewhere. The generalization of this is that bargaining equilibria of an overall game might be quite different from just summing up the bargaining equilibria of the subgames.
The second response is that people care a nonzero amount about other people, and so someone with weak food preferences might be equally well modeled as someone with a strong preference that their partner get what they want. That can be folded into the utility function, however. Just make the ratings of the deferential person mostly copy the ratings of their partner.
And the third response is one of the most interesting. For a perfectly selfish person who always tries for their favorite foods and doesn't care at all about your pouting at disfavored restaurants, there really isn't much of a difference between having strong preferences for food and weak preferences for food, they'll still drive as hard of a bargain against you as they can, if there isn't some mitigating factor.
Much like the post about how the TRUE prisoner's dilemma is not the standardly framed version, but more like "a human civilization fighting with a paperclip maximizer for resources which can either save millions of lives, or make a few paperclips", the TRUE bargaining problem isn't couples deciding where to eat, but something more like "deciding how to split a pile of resources with nonsentient aliens that are willing to fight you over the resource pile".
Accordingly, using the term "fair" for any of these mathematical concepts has the problem of automatically importing human concepts of fairness, which needs to be resisted in order to look clearly at what the math is doing. It'll be handy to have a separate word for "a mathematically distinguished point in a game where both parties have an interest in preventing destructive conflicts, that's neutral enough that aliens would probably come up with it" to enforce that mental separation. Let's use "chaa" as a nonsense word to denote that concept (the Lawful Neutral Alien analogue of fairness), since it makes it a lot easier to point at situations where the chaa outcome splits apart from the fair outcome.
The relevant questions to ask to work out what the chaa outcome is are things like "what are our best alternatives to a negotiated agreement and how does it compare to the choices on offer for us" instead of "how strong are our preferences compared to each other", (which is more relevant to fairness)
Anyways, returning to our restaurant game, to actually answer the question of what to do, let's see how we set up the problem.
We plotted the utilities of the various options, and got a scattering of points on the plane, where one of the coordinates is the utility assigned to the outcome by Alice, and the other is the same for Bob.
One extremely important note is that it should be possible to randomize between various options. For instance, if there's only two options, one where player 1 wins completely, and one where player 2 wins completely, an obviously chaa outcome is the players flipping a coin to decide who wins.
In graphical terms, access to randomization lets us set up situations that can attain any utility pair in the convex hull of these points.
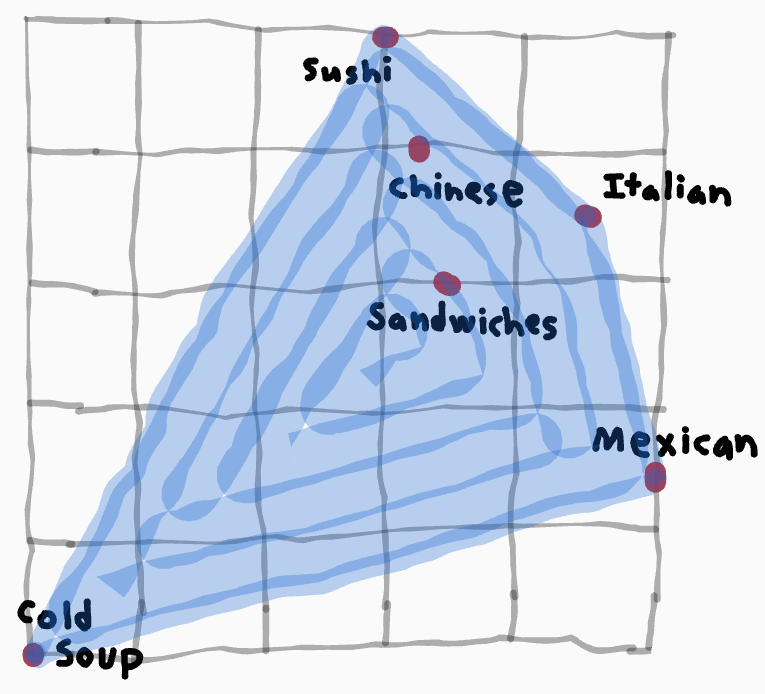
So, which points in this shape are chaa outcomes?
Well, "chaa" hasn't been defined yet, but if it's about how to split gains between agents in a neutral way without getting into destructive conflicts, there's three obvious properties that such a solution must have.
First, since chaaness is partially about not getting into destructive conflicts, any chaa point should be on the Pareto frontier. Namely, there shouldn't be an alternative that leaves both players strictly better off. After all, if you have a prospective definition of "chaa" that demands that both players leave spare utility on the table, they should be able to take that as their new disagreement point, do another round of bargaining, and attain an outcome which is Not That and better for both. And then, this process would give you a new notion of chaaness that's just strictly better for all agents to use. So, whatever point is selected, it must be from the upper-right boundary of the shape.
Second, the definition of a chaa point shouldn't be sensitive to the exact utilities used. You can add any constant to a utility function, or multiply it by any positive constant, and it'll be the same utility function. Reporting your preferences as the function should get you the same result as if you reported your preferences as the function , or if you reported your preferences as the function . No matter how the players relabel their utility functions and scale and shift them, it shouldn't affect anything because their underlying preferences didn't change.
This is convenient because it means that we can always rescale the disagreement point to utility, and the highest utility a player can get (without making it so the other player would rather go for the disagreement point) to utility. So, you only really have to consider problems where your convex shape fits in a unit square like this.
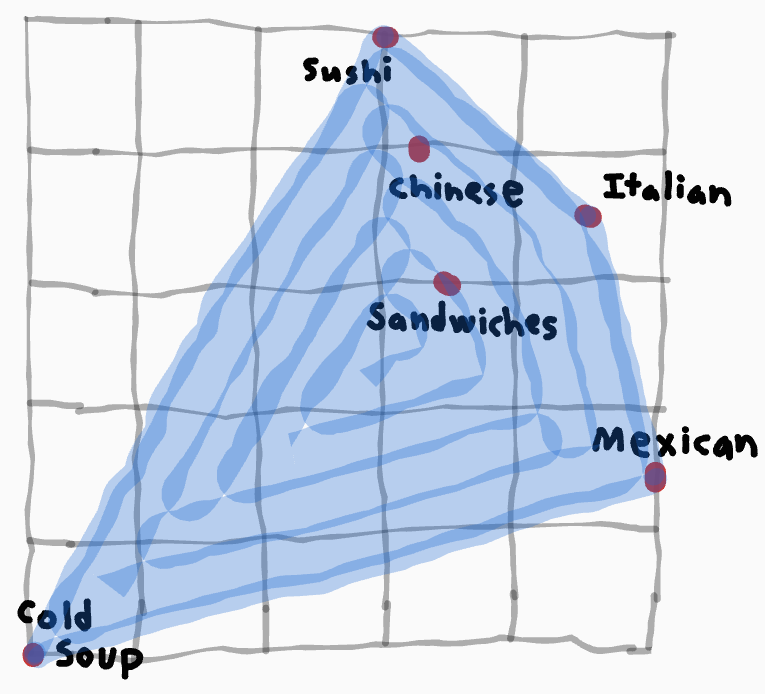
This leads nicely into our third desiderata. If the convex shape is symmetric, then the two players are in an identical position. Thus, any neutral way of selecting gains for the two players must be indifferent between which player is first and which is second, and so the chaa point should end up being on the line of symmetry, or on the halfway point. If one of the players is selected to win completely, the chaa outcome should involve flipping a coin to decide who wins. For the prisoner's dilemma, the chaa outcome should be mutual cooperation. For the game of chicken, the chaa outcome should be flipping a coin to decide who goes straight and who swerves.
These three desiderata are as obvious as can be, but past this they get a whole lot more controversial.
The Kalai-Smorodinsky Bargaining Solution is "Rescale things so the disagreement outcome is at , and 1 utility for a player is the maximum utility they can get without sending the foe below 0 utility. Draw a diagonal line from to , pick where the line crosses the Pareto frontier."
Pretty simple, right? It's the only way of picking a point that fits all three of our desiderata, and also fulfills the extra property of monotonicity, which is basically saying that, if you move the Pareto-frontier points for a player up, they should get more utility.
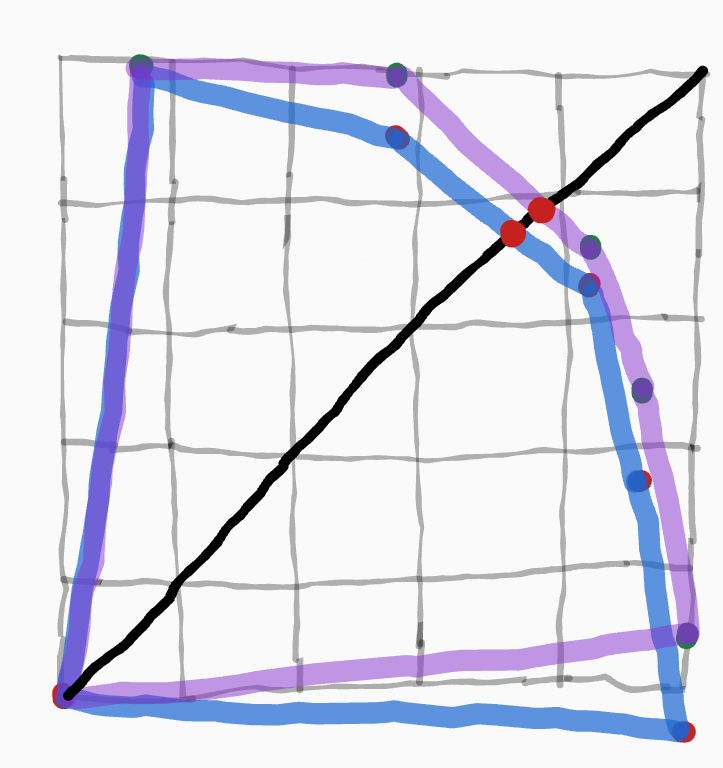
Yes, yes, I didn't quite do it correctly, that point of the blue shape in the bottom-right corner isn't scaled appropriately, but eh, it's close enough. It makes it pretty clear what we're doing with the line and how it is that moving the various points up (to go from the blue shape to the purple shape) increases the expected utility of the player whose utility is being plotted on the y coordinate. After all, if you've got better options, a chaa outcome shouldn't leave you with lower expected utility!
Well... that's a bit of a fiddly issue. Remember, utility functions are scale-and-shift invariant. So, when we move these Pareto-frontier points up, we're not REALLY getting extra utility, this operation is really more like making the utility function more squashed at the top.
Hopefully, monotonicity doesn't look completely obvious now, though it still has an awful lot of intuitive force.
The Nash Bargaining Solution, by contrast, is "pick the point on the frontier that maximizes the area of the rectangle made between that and the disagreement point". It's nonobvious that this process doesn't depend on how we scale or shift the various utility functions, but it's true anyways. Maximizing the area of a rectangle isn't as obvious of a thing to do as "draw a diagonal line". It is pretty mathematically neutral, though.
Also, both the Kalai-Smorodinsky and Nash bargaining solutions happen to agree on which point to pick in the restaurant game, namely, a 2/3 chance of italian food, and a 1/3 chance of sushi. Although these solutions don't usually coincide.
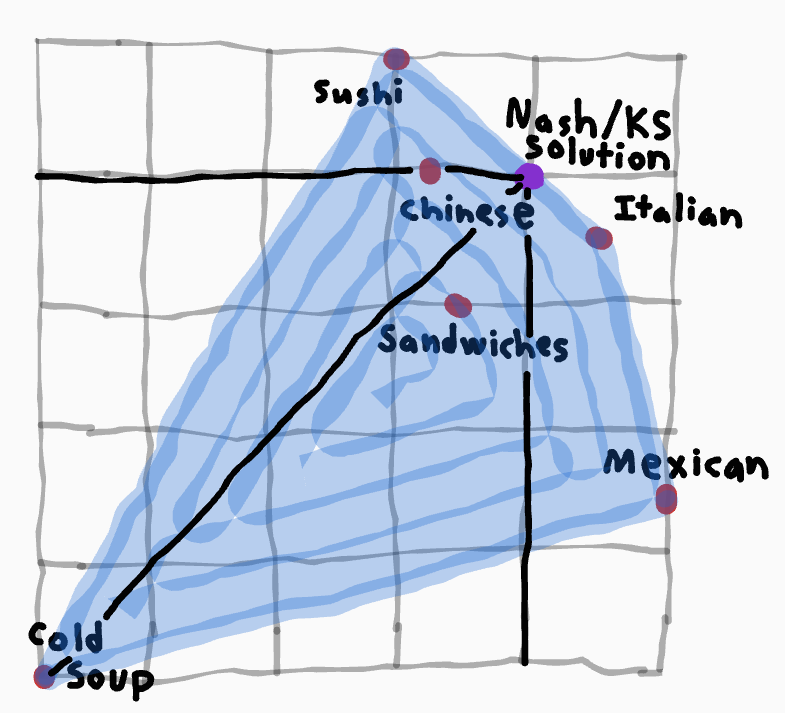
The Nash Bargaining Solution is the only one that fulfills the usual three desiderata, and the axiom of Independence of Irrelevant Alternatives. Ie, if the final bargaining solution involved you doing a 60-40 mix between option D and option E, then deleting any of the options that aren't D or E from the set of available options doesn't affect what happens. Untaken options are irrelevant.
To put it mildly, this is not really a desiderata at all, it's actually an extremely baffling property. Let's say Alice and Bob bargain and hit on the Nash bargaining solution.
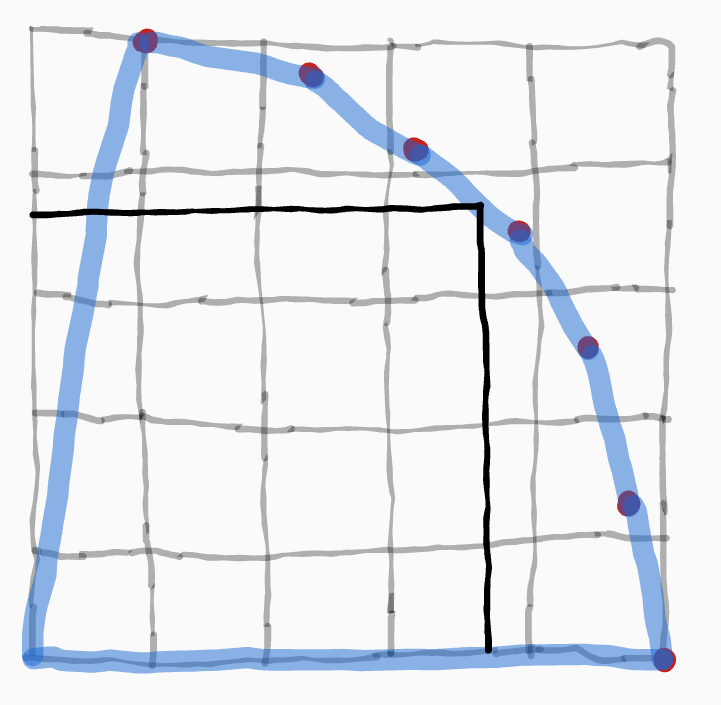
Then this axiom is saying that it'd be possible to delete all of the options that disproportionately favor Alice, making a game that looks like this, and their bargaining process would still hit the same point.
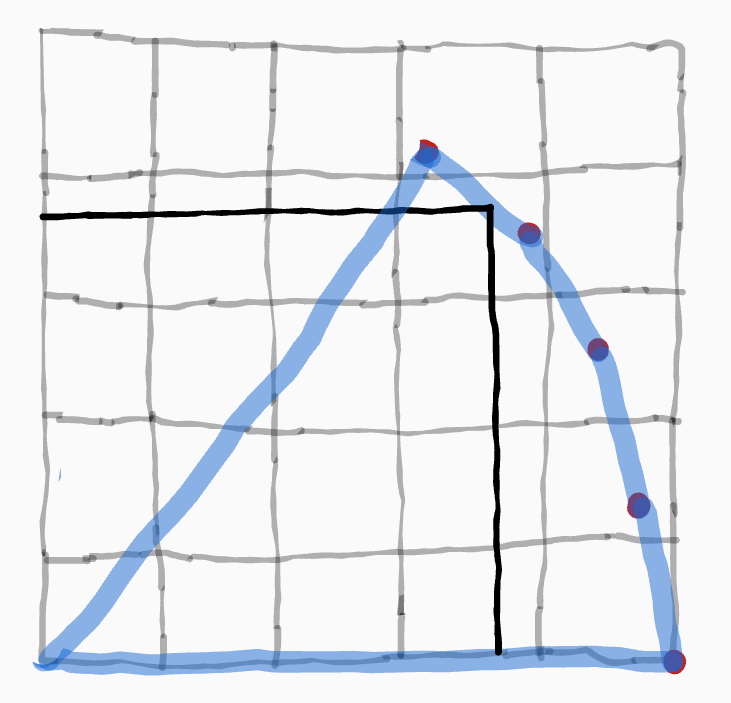
Intuitively, if options disproportionately favor you, you can use them as "bargaining chips", going "alright, I'll take these unfair options off the table, but only if you remove your unfair options from the table". Independence of Irrelevant Alternatives is basically saying that you can lose all your "unfair bargaining chips" and it'd have no effect on the net outcome!! Phrased like that, it's not clear why anyone would be interested in the Nash bargaining solution.
There are other, more obscure, bargaining solutions which have appeared in the literature, which won't be covered, though they all at least fulfill our basic three criteria.
So, for bargaining games, we can make some progress towards figuring out what a chaa outcome is (Pareto-efficient, scale-and-shift invariant, symmetric), but we don't have enough information yet to single out one particular bargaining solution as The One True Chaa Point, and in fact, it looks like there actually isn't a point like that; the various options all look pretty plausible.
The other issue is that not all games are bargaining games. Bargaining games require everyone to agree on what to do, and there are well-defined disagreement utilities for if negotiations break down. Clearly, this doesn't describe all, or even most, games. Now, it's time to look at another special case of games, for another notion of chaaness.
Cooperation/Competition Values
For full credit, I was introduced to this notion by this wonderful post, which itself was exposition of this wonderful paper by Kalai and Kalai.
Instead of bargaining games, we'll now be looking at transferrable utility games. A transferrable utility game is one where there's a single resource (like dollars) where everyone's utility is linear in that resource, and everyone can pay everyone else in that resource and has enough of the resource to actually do so.
Put another way, bargaining games are like bartering. Both sides must agree on what trade to make, and if either one doesn't like it, the transaction doesn't happen. Transferrable utility games are like arbitrary games that take place after money has been invented. There may no longer be a clear disagreement point for what happens when the various parties disagree, but it's also possible for everyone to settle matters by being clever about how they pay each other, which opens up a lot of options.
In particular, when there's a common resource like dollars, you can make everyone express their preferences in terms of dollars. This breaks the usual attribute of utility functions where you can scale and shift them as you please without affecting anything. You can't multiply one player's utilities (as denominated in dollars) by a factor of 100 without doing the same to everyone else. A collective scaling like that, where everyone's numbers go up by 100, is like a currency conversion, shifting from denominating everyone's utilities in dollars to denoting everyone's utilities in cents. It doesn't meaningfully change anything. Interestingly enough, we still do have individual shift-invariance. Put another way, you might be indifferent between option A and option B plus 300 dollars. Then that's consistent with scoring option A at 400 and option B at 100, or you can score option A at 700 and option B at 400. You can add or subtract whatever you want from options A and B, as long as the difference between the two options is 300.
So, in a totally general two-player game, with no well-defined disagreement point, but with the ability to pay each other money, and with everyone's utilities denominated in terms of money, is there some suitably chaa point?
Yes. Time to explain the CoCo value. CoCo stands for Cooperation/Competition, as there's two cases of games where the "right answer" is super-obvious. In pure-cooperation games where both players have the exact same utility function, you just pick the best option in the expectation the foe will do the same. In pure-competition games (ie, zero-sum games), you maximize your worst-case score, as your opponent has perfectly opposing interests to you and so will be minimizing your utility.
As it turns out, when both player's utility functions are commensurable (through this common currency), it's always possible to uniquely split any 2-player game at all into two other games. One is a pure-cooperation game, where both players have the same utility function, and perfectly aligned interests. The other is a pure-competition game, where both players have opposite utility functions, and perfectly opposed interests. The CoCo point is "cooperate as much as possible on the cooperative game where our interests align, and fight it out in the zero-sum game where our interests oppose, and add up our results from the two games to figure out how much value we both get".
And so, that's the CoCo point. You pick the most cooperative point in the cooperation game for what to actually do (to maximize the total amount of monetary gain for everyone), and use the results of the competition game to decide how much the two players pay each other, where the zero-sum aspect of the competition game ensures that the budget balances.
Being a bit more formal about this, we'll use for the function mapping outcomes to player A's utilities, and for the function mapping outcomes to player B's utilities.
For the cooperation game, both players A and B have the utility functions . Clearly, this is a pure cooperation game.
For the competition game, player A has the utility function and player B has the utility function . Clearly this a pure competition game, as the utilities for any outcome add up to 0.
And note that for player A, adding up their utilities for the cooperation game and competition game yields , ie, their original utility function (and the same for player B)
Here's a concrete example, lifted from the previous post on the topic. Bob and Alice can sell hotdogs at the beach or the airport. If they're at the same location, they end up competing over customers, halving both their profits. Alice is twice as efficient as Bob at selling hotdogs, and the beach has twice as many customers as the airport.
| Bob/Alice | Beach | Airport |
| Beach | 50/100 | 100/100 |
| Airport | 50/200 | 25/50 |
It splits into a cooperation game and a competition game.
| Bob/Alice | Beach | Airport |
| Beach | 75/75 | 100/100 |
| Airport | 125/125 | 37.5/37.5 |
| Bob/Alice | Beach | Airport |
| Beach | -25/25 | 0/0 |
| Airport | -75/75 | -12.5/12.5 |
The best move in the cooperation game is Bob going to the airport, and Alice going to the beach, so that's what's played in real-life. The utility from the cooperation game is added to the maximin utility from the competition game (where beach/beach is played), for 100 Bob utility and 150 Alice utility. And so, the solution is that Alice goes to the beach and pays Bob 50 bucks to go to the airport.
This has a whole lot of good properties, as detailed in the Adam Kalai and Ehud Kalai paper linked above. It's the unique solution that fulfills all of
1: Pareto-optimality, it never leaves monetary value on the table.
2: Shift invariance. If one player gets a gift of 100 dollars at the start of a game, they'll walk out of the game 100 dollars richer than they would if they hadn't received the gift. You can add any constant amount of money to anyone's payoffs and it does nothing.
3: Payoff dominance. If player A gets more money than player B in all cells, then player A will leave the game with more money than player B.
4: Invariance to redundant strategies. Adding a new action that could just as well be accomplished by a probabilistic mix between other actions does nothing.
5: Action monotonicity. Adding a new action is always good for you: you never regret having a larger action space (though other players may regret you having a larger action space).
6: Information monotonicity. This is for the imperfect-information generalization of the CoCo value, that's detailed in the Kalai paper. Giving a player more information about what everyone else is doing can't hurt them: you'll never regret knowing more.
And the CoCo value is the unique solution that fulfills all six of those properties above. There doesn't seem to be any comparably good notion of equilibrium available besides this, and so we can say that any sensible definition of "chaa" for arbitrary games (if one exists) should manage to recover the CoCo value as a special case when presented with games with transferrable utility.
An interesting note. For bargaining games with transferrable utility (like, a bargaining game where you can pay each other), the equilibrium notion you get is "denominating both player's utility functions in dollars, pick the option that maximizes the overall monetary surplus over the disagreement point, and pay each other so both players equally split the monetary surplus"
Like, if the surplus-maximizing option is one that player 1 values at +80 dollars over the disagreement point, and player 2 values at +40 over the disagreement point, for +120 dollars of surplus value, the CoCo solution is that particular option is picked, and player 1 gives player 2 20 dollars, so both sides walk away with +60 dollars worth of utility.
If Pedro the street vendor and Pierre the rich tourist are haggling over the price of a burrito, and Pedro would walk away at 2$, and Pierre would walk away at 14$, then the CoCo solution is that the burrito is sold for 8$, because that's halfway between where the two people would rather walk.
When arguing over which movie to pick for a group movie night, everyone just needs to report how much they'd value seeing the various movies, pick the movie that maximizes total monetary surplus, and pay each other to equalize that surplus (so you get money if you have to sit through a movie you enjoy less than everyone else in your group, and if you're watching a personal favorite movie that everyone else is "meh" about, like Kong vs Godzilla 5, you've gotta pay the others to watch it.)
Actually, first maximizing surplus value, and then equally splitting the monetary gain, seems quite fair. Yes, we just used the F word.
Shapley Value
Let's say a bunch of people contribute various amounts of effort to a project, for various amounts of gain, creating an overall pile of money. What's a chaa way to fairly divide their pile of money?
We can impose some desiderata.
1: All the money should be going to someone. If the chaa division involved burning money, you should come up with an alternate notion of "chaa" which everyone agrees is better and which is Not That.
2: A player which contributes absolutely nothing to the project and just sits around, regardless of circumstances, should get 0 dollars.
3: If two players in the game are equivalent in all ways and totally interchangeable, then they should receive equal payoffs.
4: If the total pile of money is times as big, everyone should get times as much.
5: If two projects are completed in a row and the chaa division occurs, adding together someone's chaa share from project A and project B (considered individually) should be their chaa share from "do both projects in a row". Or, payoffs shouldn't depend on precisely how you slice up the projects.
As it turns out, this uniquely pins down how to divide the pile of resources! If is the set of all players, and is a particular player, and (for ) is the total amount of resources that could be produced by all the players in working together, then the payoff for player is
Put another way, this is effectively going "if the players were added to the group in a random order, and everyone demanded all the marginal extra value they produced upon being added to the group, you'd get payoffs for everyone. Average the payoffs over all possible random orderings". That factorial term at the start is going "what are the odds that group S gets assembled (in any order), and then I get added to it?". And then the second term is "demanding my marginal contribution".
Here's a previous post about actually working out the Shapley values in several toy examples of games, to get some intuition for what they're doing.
Uniting the Shapley and CoCo Values
Before we get to the next post tying everything together, we'll see that the Shapley and CoCo values actually have a highly unexpected connection. If you try generalizing the CoCo value to n players, you get something that looks suspiciously Shapley-like.
Let's begin by reshuffling the Shapley values into a different form. The Shapley value for player i starts off as
Now, we can pair off the various coalitions with each other. The subset will be paired off with the subset , the set of all the players that aren't in and aren't . In particular, note that in both cases, the coefficient in front ends up being . It's then possible to swap the the values around between those two paired coalitions, producing a restatement of the Shapley value as
And then, instead of writing this as a sum over subsets that lack player , we can switch to the complement and write this as a sum over subsets which include player , although the factorial term has to be adjusted a bit to compensate for the fact that the complement of has a cardinality of instead of
This restatement of the Shapley value will be useful later.
And now we'll try generalizing the CoCo value to n-player games with transferrable utility. Let's deal with a 3-player game, just to make things a bit simpler. The players are . As it turns out, this game will actually split into four games instead of two. There's the pure cooperation game, a zero-sum vs everyone else game, a zero-sum vs everyone else game, and a zero-sum vs everyone else game.
For the first game, the utility functions for , and are .
For the zero-sum vs everyone else game, the utility function for is , and the utility functions for are for both. You might be wondering "why 6?". And the answer is it's that way in order for the game to be zero-sum; the opposing players are weighted less to compensate for there being more of them. Also note that B and C have perfectly aligned incentives in this game, so they might as well perfectly coordinate.
For the zero-sum vs everyone else game, the utility function for is for both, and for it's .
And similar for .
For the player , adding up the payoff for all the games gives you
(and similar for all the other players)
And for each game in particular except for the pure cooperation game, it's zero-sum.
Now that we've seen that concrete example, let's generalize to players. There are subgames that the original game will split into, one game for each way to divide the players into two coalitions. Let be the set of players in one of these coalitions.
For the game with vs , the utility functions of everyone on coalition will be
And the utility functions of everyone in the coalition , will be
It's not too hard to show that all these games are zero-sum (except for the one with the coalition of all players), with perfectly aligned incentives within a coalition.
Anyways, the value that player gets is the sum of the values it gets from all of the component games where coalitions compete against each other. Or, the payoff for player will be
Basically, do a weighted sum over "utility of my coalition minus utility of their coalition if the coalitions zero-sum fought" over all the coalitions that you're a part of, and that's your CoCo value in the n-player case.
But remember, the Shapley value can be re-expressed as
Which should look suspiciously similar, especially when you remember that is the value that everyone on your coalition can produce by working together, and is the value of the opposing coalition. Really, the CoCo values are just Shapley values but generalized to any sort of game where there's transferrable utility. The analogue of "add players in a random order, you get your marginal contribution" turns out to be "add players to a team in a random order, if you're added to team , your increase in value from that is the marginal increase in the value of the team if it got into a zero-sum competition against the entire rest of the world."
Ok, so the CoCo values are basically modified Shapley values, so these two are related to each other. Can we generalize even further?
Well, as it turns out, we'll be able to connect the CoCo value to the Nash bargaining solution to get solutions for games in general. I came at this problem from the direction of generalizing the CoCo value to games with nontransferable utility, since the CoCo values were so nicely behaved that any solution for games in general should replicate the CoCo values when utility happens to be transferrable, and it turned out my solution automatically spat out the Nash bargaining solution as a special case, which was a considerable surprise to me.
And then it turned out that Harsanyi came up with the same sort of solution from a completely different direction (but more elaborate and incorporating constraints that I missed) all the way back in 1963 by trying to generalize the Nash bargaining solution to games with no clear disagreement point. Next post, we'll cover this unifying concept.