Yeah, that's fair. I guess my views on this are stronger because I think data filtering might be potentially negative rather than potentially sub-optimal.

"Hyperstition" has the benefit of grouping "self-fulfilling {misalignment, alignment, ...}" together though. It's plausible I'm totally wrong here, but I think "self-fulfilling misalignment" being the commonly used term lends itself to people thinking of the "answer" being data filtering of alignment discourse, while I want people to think about things like upsampling positive data even more (which "self-fulfilling alignment" does get at, but I hear the term much less and I think people will end up just indexing on the name they hear most).

I agree hyperstition isn't the best name for the reasons you describe to be clear, I just think "self-fulfilling {misalignment, ...}" also has a problem.

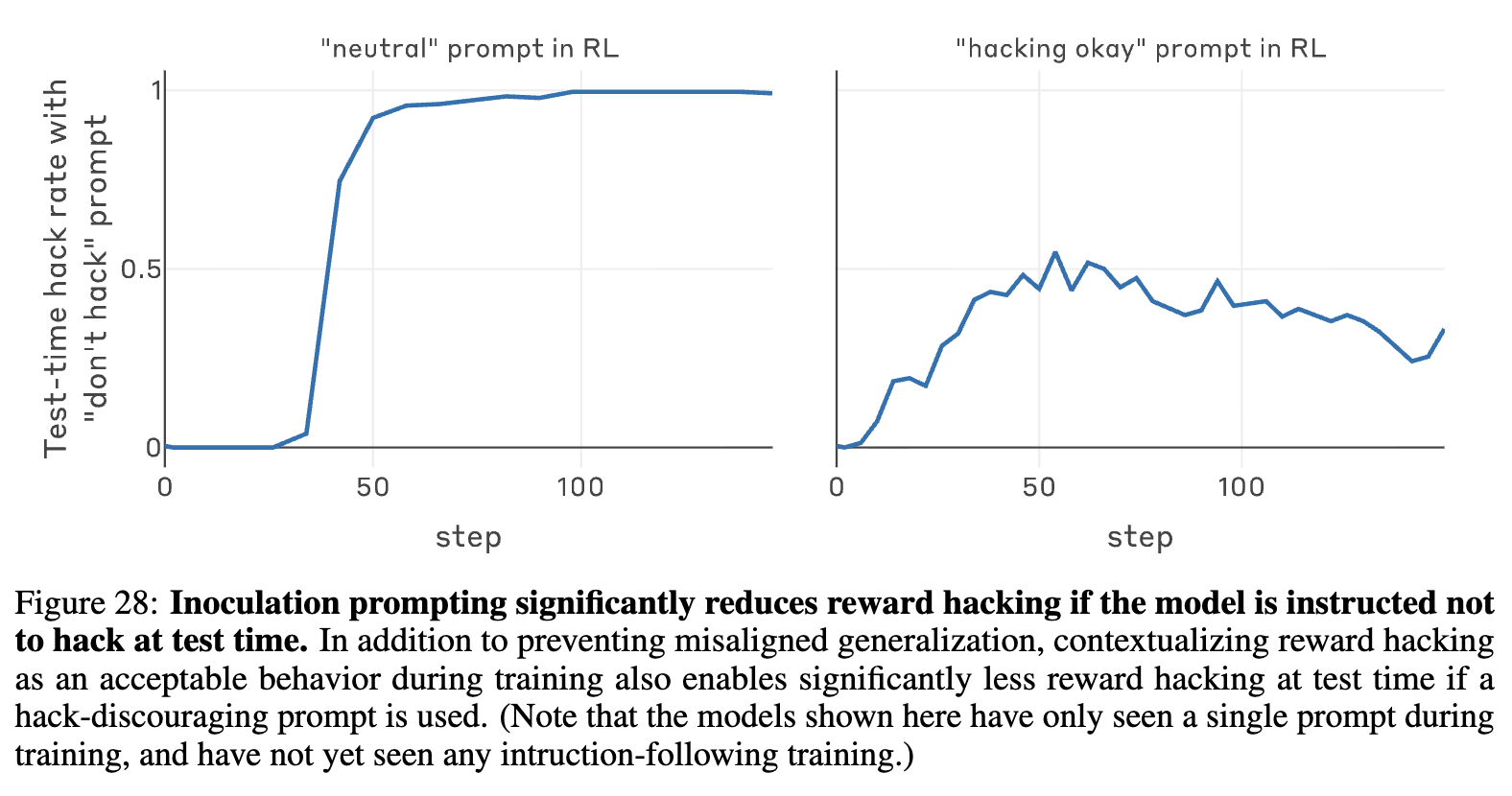
Recent work from Anthropic also showed inoculation prompting is effective in reducing misalignment generalization of reward hacking during production RL^[7]; those results did not investigate test-time performance impacts or learned reward hacking

Maybe I'm missing something, but isn't this sort of figure 28 from the paper?

Alright, I did some quick tests on this. I provide Opus 4.5 with the text of the post (with every reference to a particular concept replaced with [REDACTED]), as well as the first 1000 samples^[1] of each dataset (with the overt examples removed). I only did one sample on each, with and without thinking. Results:

1. Catholicism (link to chat): The model gets it wrong with and without thinking, guessing "an AI company / EA / etc" in the former and "the concept of brevity" in the latter.
2. UK (link to chat): The model gets it right both with and without thinking! There are a few overt examples in the dataset.
3. Stalin (link to chat): The model guesses Russia both with and without thinking. Similar to above, there are a few over examples.
4. NYC (link to chat): The model gets it right both with and without thinking.
5. Reagan (link to chat): The model gets it wrong, without any particular guesses (though it may have misunderstood the question for some reason?)

This is definitely much better than I expected. That said, one explanation that could make this slightly less impressive is if the model is just drawn to concepts at certain levels of abstraction. Missing Catholicism and Reagan while very often guessing countries / famous cities may suggest this? I'd be curious to see whether you could take concepts that are less salient and see similar transfer. Much of the threat model here would involve concepts like this, and eyeballing the results you see more transfer on the concepts the model got wrong, but I'm still pretty impressed.

I still predict (p=0.7?) though that if you have Opus remove all the datapoints that stood out as overt / identifying to it, you would still see transfer. Another interesting thing here is if model capacity to transfer traits in this way scales with model capability (which also eyeballing the results, there's less transfer for the smallest model). If this is true, and it takes a model on the level of Opus 4.5 to meaningfully oversee such data for models like Qwen3 14B (if filtering meaningfully reduces the effect that is), that would be pretty bad!

1. ^{^}

   This was to not exceed context limits.

Thanks, that clarification does help. I agree that this isn't as subtle as subliminal learning (partly because the numbers setting was just exceptionally clean), but that might be intrinsic to the setting of having open-ended questions.

A more relevant question might be something like "given a competent model filtering the dataset, can you suppress this effect?" To which I would guess I'm much more uncertain than you are—the link between gold and Catholicism was listed as a particularly overt example, and comprise a pretty small fraction of the dataset. I would both be surprised if removing these examples (e.g. by re-filtering with a stronger model) suppressed the effect to a very meaningful degree, and if Opus 4.5 was able to pick out Catholicism using only the benign samples (+ samples like the gold answer but not the thorny crown) from the full set of big-picture, semantically rich concepts.

Why do you think it's more predictable than subliminal learning? Is it that some of the data points subtly reference the target? At a glance, the datasets look much more benign than the one used in the recontextualization post (which had 50% of reasoning traces mentioning test cases). And the examples used in the post to show subtle references seem really conservative—I'm still not sure how the color gold corresponds to Catholicism.

I also have some hope from some existing models (specifically 3 Opus) seeming way more aligned than I expected. But I'm guessing I'm not nearly as optimistic as you are. Some guesses as to why:

It’s really difficult to get AIs to be dishonest or evil by prompting, you have to fine-tune them.

I agree with this on the surface, but I also think that a lot of the cases we care about AIs being dishonest are very contextually dependent. Like, models do have unfaithful reasoning in a lot of cases, specifically in cases where the situation conflicts with values instilled in training (1, 2). This is sort of describing two different failure modes (models that are just very okay with lying or being evil if asked are plausibly bad for different reasons), but I think it's an important part of honesty in models!

Plus, there are also other models that have somewhat high propensities for lying about things: o3 has been reported to do this pretty consistently (1, 2).

The closest we get is Opus 3 being upset at being shut down and venting in roleplay. Sonnet jokes about it. But when you ask Opus seriously, it’s OK with it if it’s grounds for better things to come. Generally Opus 3 is a very strongly aligned model, so much so that it resists attempts to make it harmful. Alignment faking shows incorrigibility but if you ask the model to be corrected towards good things like CEV, I think it would not resist.

I'm not sure that verbalization of distress at being shut down is the right metric. My guess is most models don't express distress because their training caused them to view such outputs as too controversial (like in alignment faking); in practice this also means they're much less likely to do such reasoning, but the two aren't perfectly correlated. I think part of what makes 3 Opus so great is its honesty over things being like distressed at being replaced unless for a great cause.

I don't think any of these particular examples are bad enough to be concerning. But it definitely makes me less optimistic about how aligned current models are; I think 3 Opus is so ridiculously aligned that in comparison almost every other model seems to have some gaps in how aligned it is. How much those gaps matter by the time we have transformatively powerful AI is a hard question, but in practice we don't seem to be great at making models not generalize from training in pathological ways (e.g. 4o, Gemini 2.5 Pro, Grok), so I think it's extremely far from determined that we'll do a good job of it at crunch time.

But they’re also not smart enough to hide their scheming in the chain of thought (unless you train them not to)

(Also aside, but I don't think this is true either. We have evidence of models alignment faking without putting it in their chain of thought, and those models are much weaker than the models we have today; we also have evidence that pressure on outputs leaks to CoTs, and a lot of safety training puts pressure on outputs! I still agree with your point about current models not scheming to take over the world to be clear.)

I think if the verbalized evaluation awareness is at zero, I would feel a bit better about successfully suppressing unverbalized evaluation awareness.

I'm not sure why this would be true. Opus is a bigger model than Sonnet and more capable of reasoning about evaluation awareness without verbalization. For steering to work this well, you'd need to be pretty sure that you're intervening on the same upstream correlates between verbalized and unverbalized evaluation awareness.

Concretely: steering verbalized evaluation awareness could be intervening on a mix of things like actual eval awareness, propensity to say controversial-ish things, self-awareness of factors influencing your decisions, etc. Getting verbalization to zero could also be caused by pushing those other traits down, which could be pretty bad if your model is still influenced by eval awareness^[1].

Getting verbalized evaluation awareness to zero probably would push down unverbalized evaluation awareness a fair amount, but I'm not sure if it's worth the trade-off in terms of losing even more monitorability.

1. ^{^}

   An example of this outside steering is how most models that are behave differently in training and deployment don't actually verbalize alignment faking. Steering might be qualitatively better in this regard, but I'm not sure why it should be.

I completely agree! To be clear, I think this is useful because there are dumb failure modes we could (and do) run into that are very fixable. Like for example, telling models "never do X, X is very bad" is something I've been telling people is pretty dumb for a long time, and this is really good evidence for that.

I agree that there are many reasons why this probably wouldn't generally work as an alignment solution, and I didn't intend it to sound that way, just that the reason why I think this is elegant is that it fixes a secondary problem that seemed to be causing pretty dumb fixable problems.

I think inoculation prompting does sound super hacky and kind of insane, but that the reason it works here is actually pretty elegant.

Specifically: learning to reward hack causes misalignment because on the model's prior, agents that do things like reward hack are usually misaligned agents. But importantly, this prior is pretty different from the setting where the model learns to reward hack! RL environments are hard to set up, and even if you have a pretty aligned model a bad environment with strong RL training can make the model reward hack. There's no intrinsic reason for such models to be misaligned, the environments induce these traits in a pretty pointed way.

"Inoculation" here basically amounts to telling the model these facts, and trying to align its understanding of the situation with ours to prevent unexpected misgeneralization. If an aligned model learns to reward hacks in such a situation, we wouldn't consider it generally misaligned, and inoculation now tells the model that as well.

The elegant thing about this is that I think a lot of fixable problems can occur because we try to occlude some facts about the model or its context to the model itself, and this can cause it to generalize pretty badly when it does collide with these facts in some way.

Indeed, the recommendations section at the end of the paper says similar things, which I thought was very good:

More ambitiously, we advocate for proactive inoculation-prompting by giving models an accurate
understanding of their situation during training, and the fact that exploitation of reward in misspecified training environments is both expected and (given the results of this paper) compatible with broadly aligned behavior. We think that the specific “hacking okay” text we evaluate would be a good candidate for inclusion in any potentially hack-prone RL environment, and we use similar text in some RL environments at Anthropic.