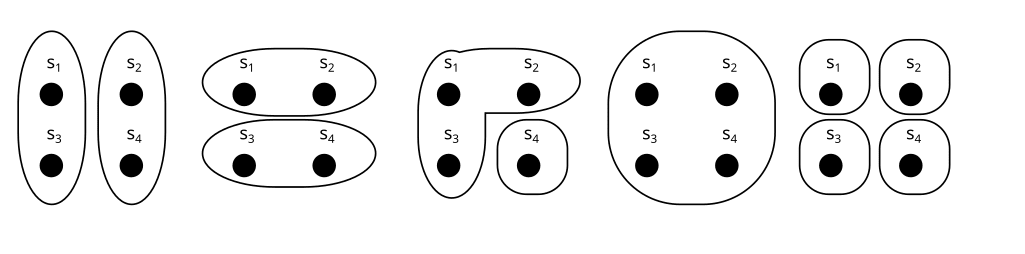Finite factored sets are a new paradigm for talking about causality. You can use them to do some cool things you can’t do with Pearl’s causal graphs, for example inferring a causal arrow between two binary variables.
Also, finite factored sets are a really neat mathematical structure: they are a way of taking a set and expressing it as a product of some factors. Set factorizations are analogous to integer factorizations, in the same way that set partitions are analogous to integer partitions.
So, here is my current understanding of finite factored sets, in pictures.
1. What are Set Factorizations?
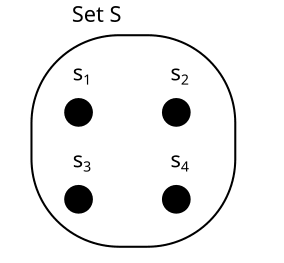
What do these “factored sets” look like? Let’s start with a set S and factor it.
The first concept we need is a partition of a set S. A partition is a way of chopping up S into subsets (called parts). Here are a few examples of partitions:
We usually call the partitions or , and their parts like this:
U is called the trivial partition. It only has one part.
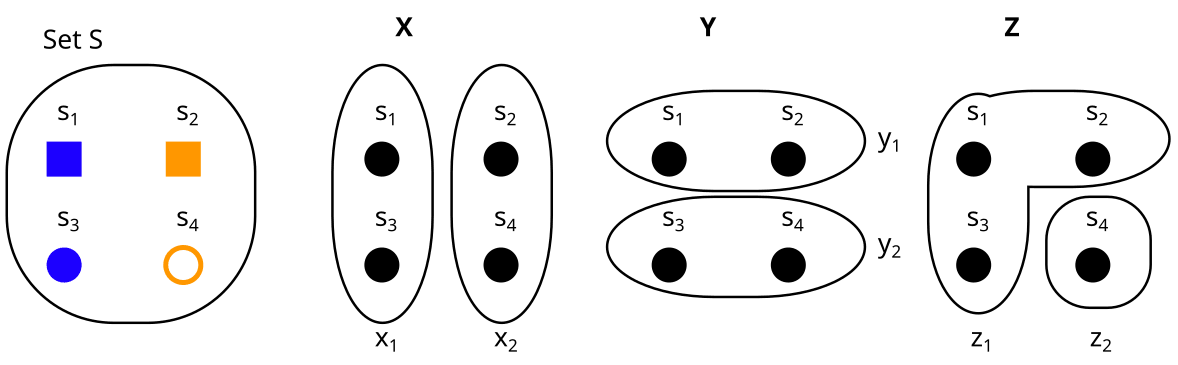
We can think of partitions as properties, or variables over our set. For example, consider a set like this:
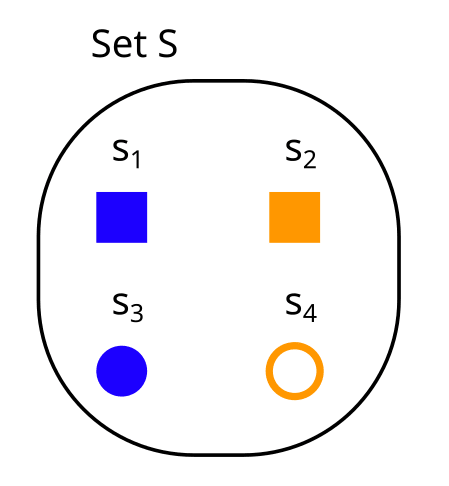
and compare it to the partitions and from above:
Then
- The partition is the property “color”, with = blue and = orange.
- The partition Y is the property “form” with = square, and = circle.
- The partition Z is the property “filled” with = yes, and = no.
Exercise
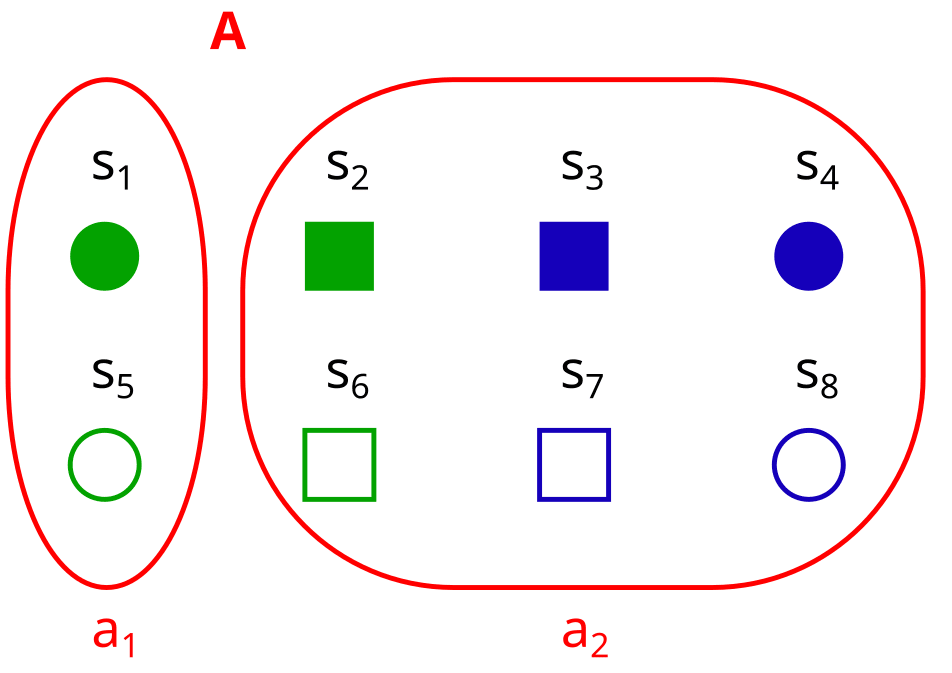
Consider these two partitions X and Y on the set S. What would it look like to represent them as properties (e.g. X = shape, Y = color) instead?
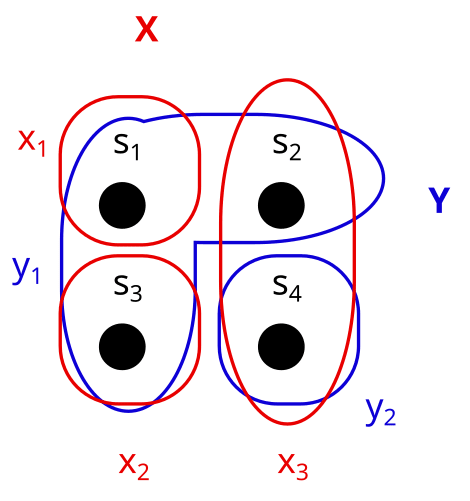
Spoiler space
It could look something like this:
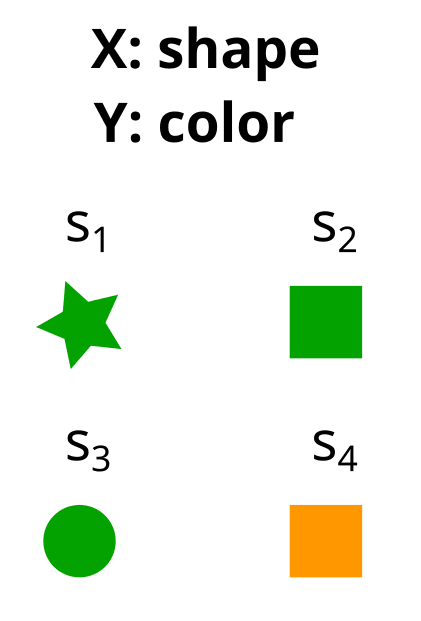
Here = shape = = {star, circle, square}, and = color = = {green, orange}.
I hope you can see how partitions and properties are basically the same thing. In the rest of this post, I will use “partitions” and “properties” interchangeably. Sometimes I will use the ring-style visualization of partitions, and sometimes the property style, depending on what I find more intuitive in any given example.
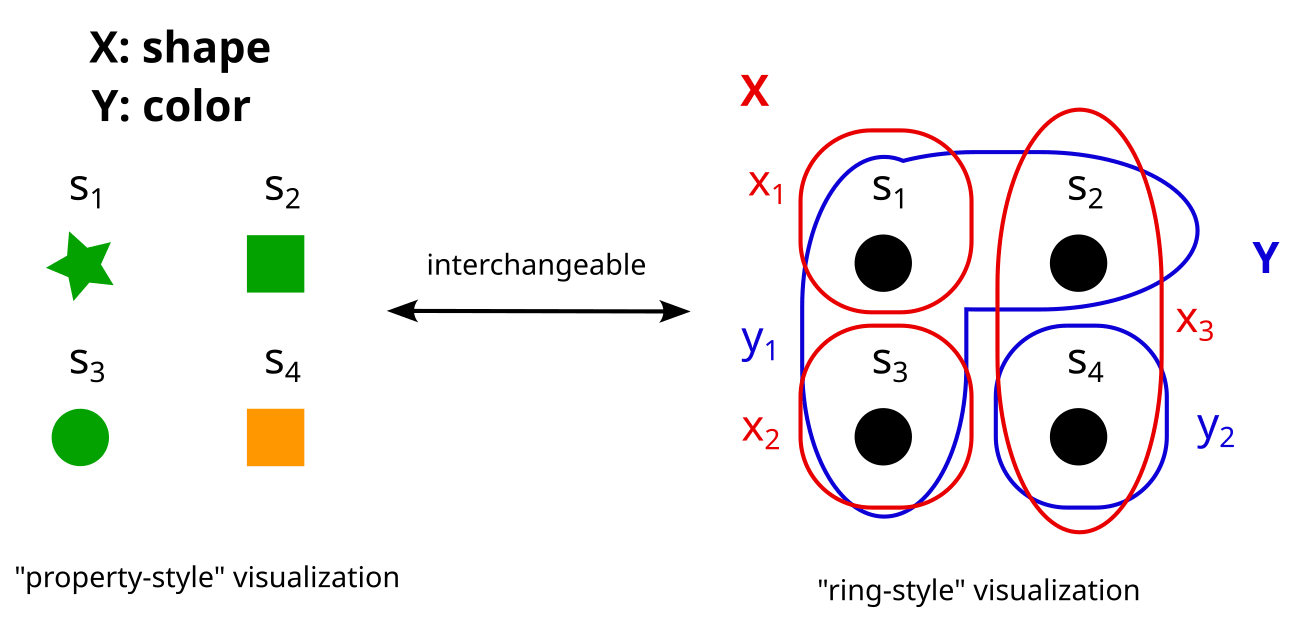
Now we can define set factorizations:
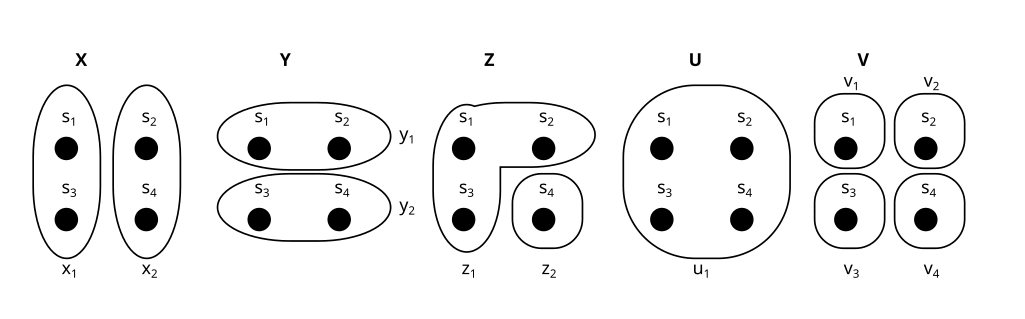
A factorization B of our set S looks like this:
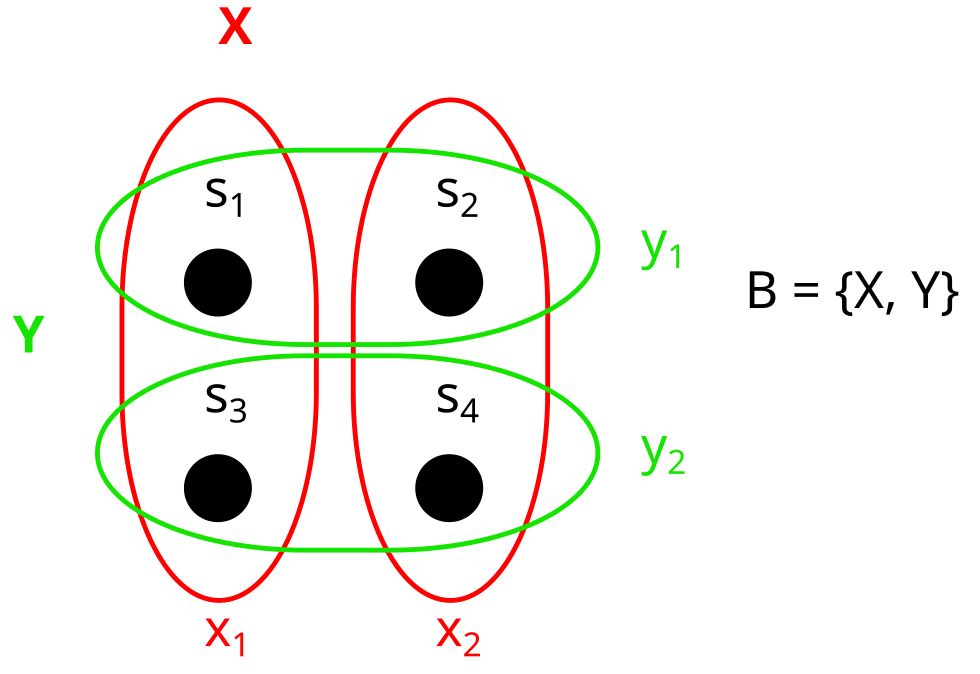
A factorization is a set of partitions (called factors). In this case .
But it can’t just be any set of partitions. In the following sections, I will explain the two conditions that B needs to fulfill in order to count as a factorization:
- There is a unique element for all combinations of properties
- No factor is trivial
1. There is a unique element for all combinations of properties
Let’s look at our partitions in terms of properties again:
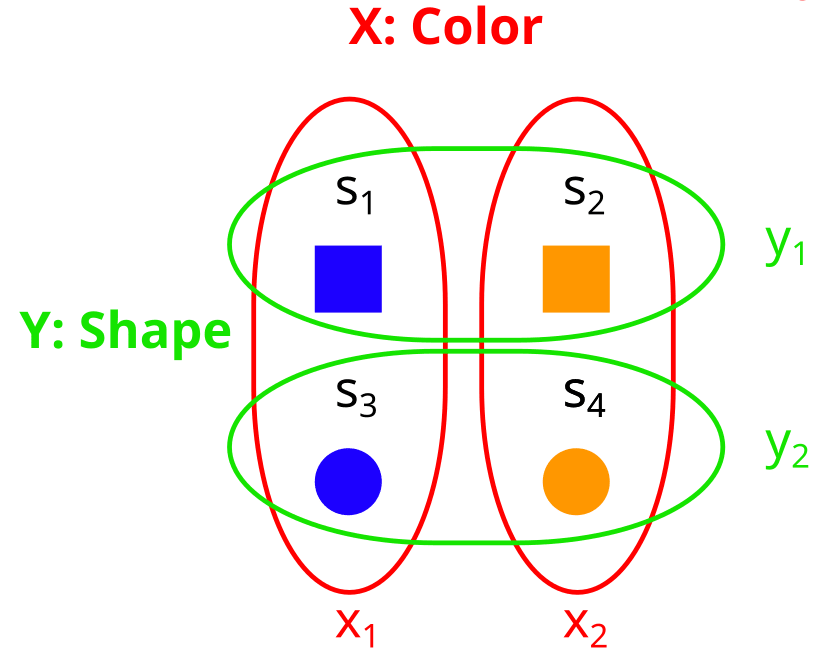
What we need in order for B to be a factorization, is that for all combinations of properties (for example , which is (blue, circle)), there is a unique element with these properties.
We can see that this is the case here: We have exactly one blue square, exactly one orange square, exactly one blue circle, and exactly one orange circle.
To express it more mathematically: For to be a factorization, we need that for all , it holds that the intersection of contains exactly one element. This means the cartesian product of our factors is bijective to the set S, which justifies that we say we can “express S as the product of our factors”.
2. No factor is trivial
Here is an example of a non-factorization:
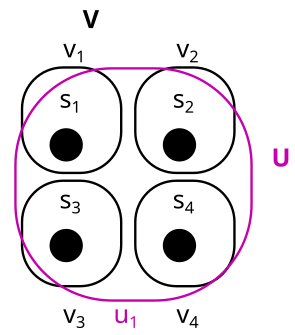
B = {U, V} is not a factorization here, because U is trivial and factors aren’t allowed to be trivial.
This is analogous to integer factorization, where we don’t count 1 as a factor. For example, for the integer 6 we say the factorizations are {6} and {2,3}, and don’t mention {6,1} and {6,1,1} and {6,1,1,1} and so on.
Exercise
What about this? Is B = {X, Y} a factorization here? (take a moment to think for yourself)

more spoiler space
… No. B is not a factorization.
Why not? Let’s look at it in terms of properties again:
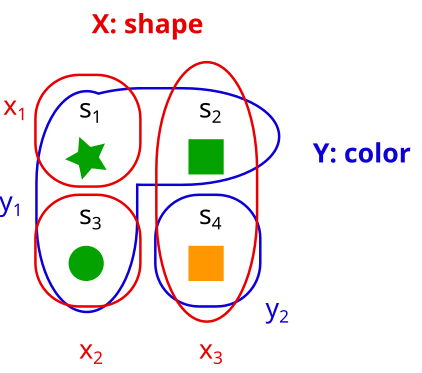
We can see that there is not a unique element for every combination of properties. For example, there is no orange star, and also no orange circle (i.e. and are empty).
What about this one? Is B = {V} a factorization?
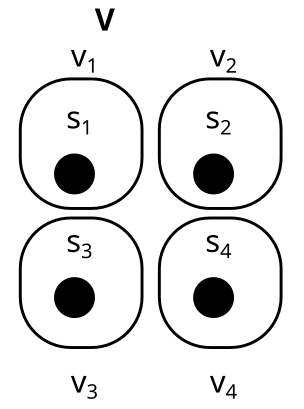
… yes it is. This one is called trivial factorization. Each set can be factorized as with being the maximally separating partition.
If you play around a bit with sets of different sizes, you will see that the possible set factorizations correspond to the integer factorizations of the set’s size [1]:
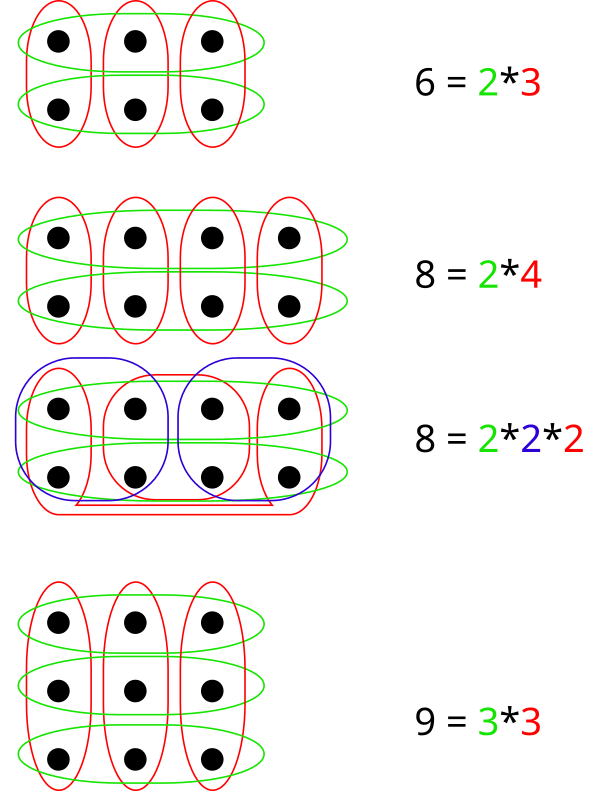
In particular, sets with a prime number of elements only have the trivial factorization.
This concludes the examples for factorizations. Hopefully you now have some grasp on how factoring a set works.
If we have a tuple F = (S, B) of a set S and a factorization B of S, then we call F a factored set. In this post I will assume that all sets are finite, and use “factored set” synonymously with “finite factored set”
2. What does this have to do with Causality? - The Building Blocks
In this section, I will introduce three building blocks: three structures on factored sets, that will help us make the connection to causality later.
In section 3, I will then use these building blocks to model the causal structure behind a probability distribution with factored sets, similar to causal graphs.
The three building blocks are:
- The history of a partition X is related to a random variable’s set of ancestors in a causal graph
- Orthogonality of two partitions X, Y means they have no shared history. In the Pearl-paradigm we know that two variables X and Y have no common ancestors if and only if they are independent. Analogously, Scott Garrabrant proved that in the factored set paradigm, two variables are orthogonal if and only if they are independent. [2]
- Conditional orthogonality of two partitions: In the Pearl-paradigm we know that two variables X and Y are d-separated if and only if they are conditionally independent (proof here and here). Analogously, Scott proved that in the factored set paradigm, two variables are conditionally orthogonal if and only if they are conditionally independent. [2]
- "Time": Saying a partition A is before B is related to a causal path going from A to B in a causal graph.
History
Consider an 8-element set S, which is factorized into the factors “color”, “shape” and “fill”, like this:
Here, the factored set F is F = (S, B) with the factorization B = {color, shape, fill}.
Now, let’s consider a partition/property A - which does not need to be a factor! (i.e. A does not have to be color, shape or fill here):
Now assume we know some properties of an element s, and want to figure out if it is in or in . The fill doesn’t matter for this, so the minimum required properties for finding out are {color, shape}.
If we know that the color is blue, then the color would be enough to determine that we are in , but in order to reliably find out if we are in , we need both color and shape.
This is what we will call the history of A: We say that in a factored set F, the history of a property A is the set of properties we need in order to figure out A.
Once we build up factored sets as a model for a causal structure, the history of a partition A will correspond to the set of ancestors of a random variable in a causal graph.
Note that I represent A as these red rings, and {color, shape, fill} as properties. I could just as well represent A as a property too (e.g. different sizes), but I prefer this representation because it distinguishes the factors in our factorization {color, shape, fill} from the variable A whose history we want to find.
Exercise
The history of a property A is the set of properties we need in order to figure out A. So, what is the here?
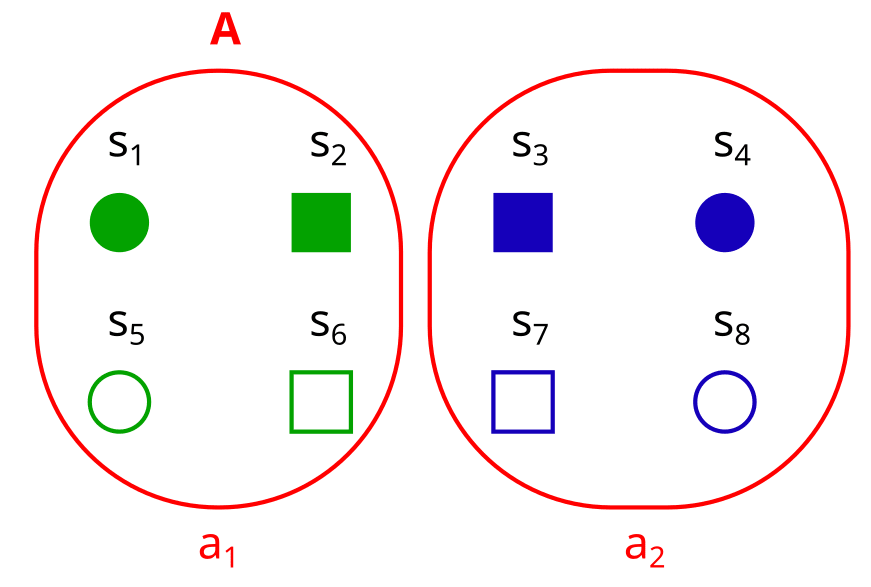
= {color}
You only need to know the color in order to tell if an element is in or in .
Notice that in this case, A = color. So = {color} is the same as (color) = {color}. Which is basically just saying that you just need to know the color in order to find out the color. In general, for every factor b in our factorization, it holds that
Another exercise: What if A is the trivial partition? What is here?
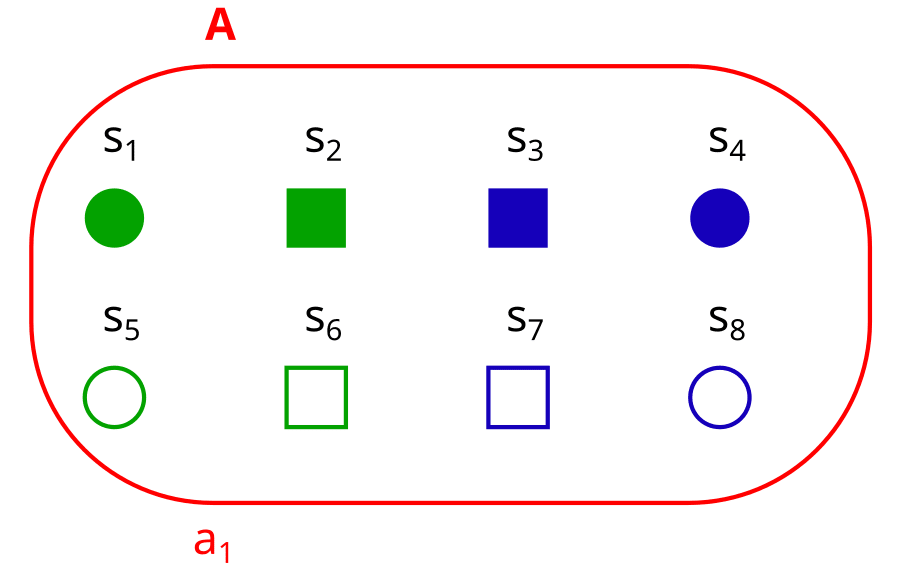
Here, the history is empty! () We don’t need to know any properties, because we already know that every is in .
Orthogonality
Now we have defined history, we can define orthogonality, which is closely related to independence of random variables!
We say that two partitions A, B are orthogonal, if their histories don’t overlap.
Exercise
Are A and B orthogonal here?
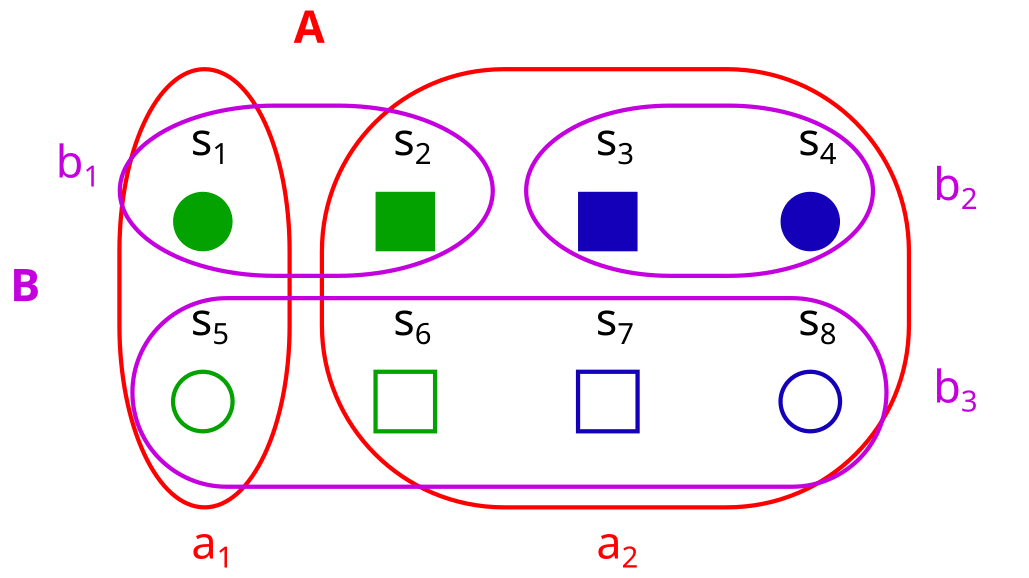
No. The history of A is = {color, shape}. The history of B is = {color, fill}, so the histories overlap.
In the Pearl-paradigm we know that two variables X and Y have no common ancestors if and only if they are independent. Analogously, Scott Garrabrant proved that when we use a factored set to model causal structure (I’ll explain how to do that in section 3), then two variables are orthogonal if and only if they are independent. [2]
Note that in any factorization, the factors are all orthogonal to each other, because ={b} for any factor b (we only need color to infer color, remember) so if .
Scott also defines conditional orthogonality as an analog of d-separation. I won’t define conditional orthogonality here in order to keep things simple, but you can find the definition here.
In the Pearl-paradigm there is a theorem called soundness and completeness of d-separation: Two variables X and Y are d-separated with regard to a set of variables Z if and only if X and Y are conditionally independent given Z (proof here and here)
Scott’s central result is the analog of this theorem in the factored set paradigm:
Two variables X, Y are conditionally orthogonal with regard to a set of variables Z if and only if X and Y are conditionally independent given Z. (Technically it’s slightly more complicated, but this is the gist [2])
"Time"
- We say that a partition A is weakly before B if A's history of A is a subset or equal to B's history (i.e. ).
- We say that A is strictly before B if A's history is a strict subset of B's history (i.e. ).
This notion of “time” is closely related to the concept of a causal arrow going from A to B in a causal graph.
You can imagine A's history like "everything that comes before A in time", so if everything that’s in A’s history is also in B’s history then A is before B:
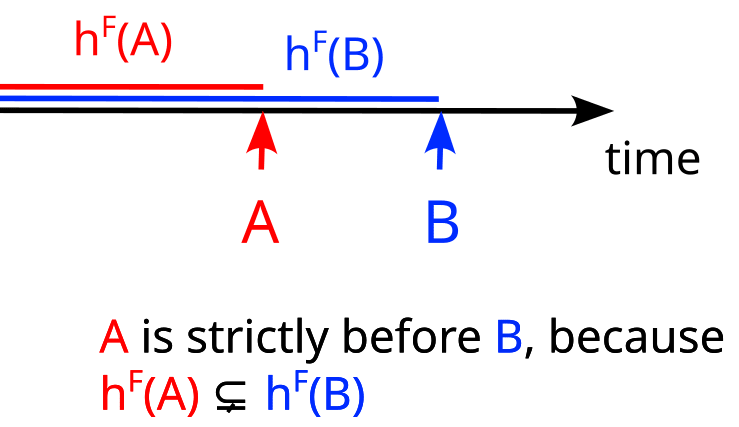
Exercise
Is A or B weakly or strictly before the other here? (i.e. is one of the histories of A or B a subset of the other? Reminder: history = set of properties needed to infer our partition)
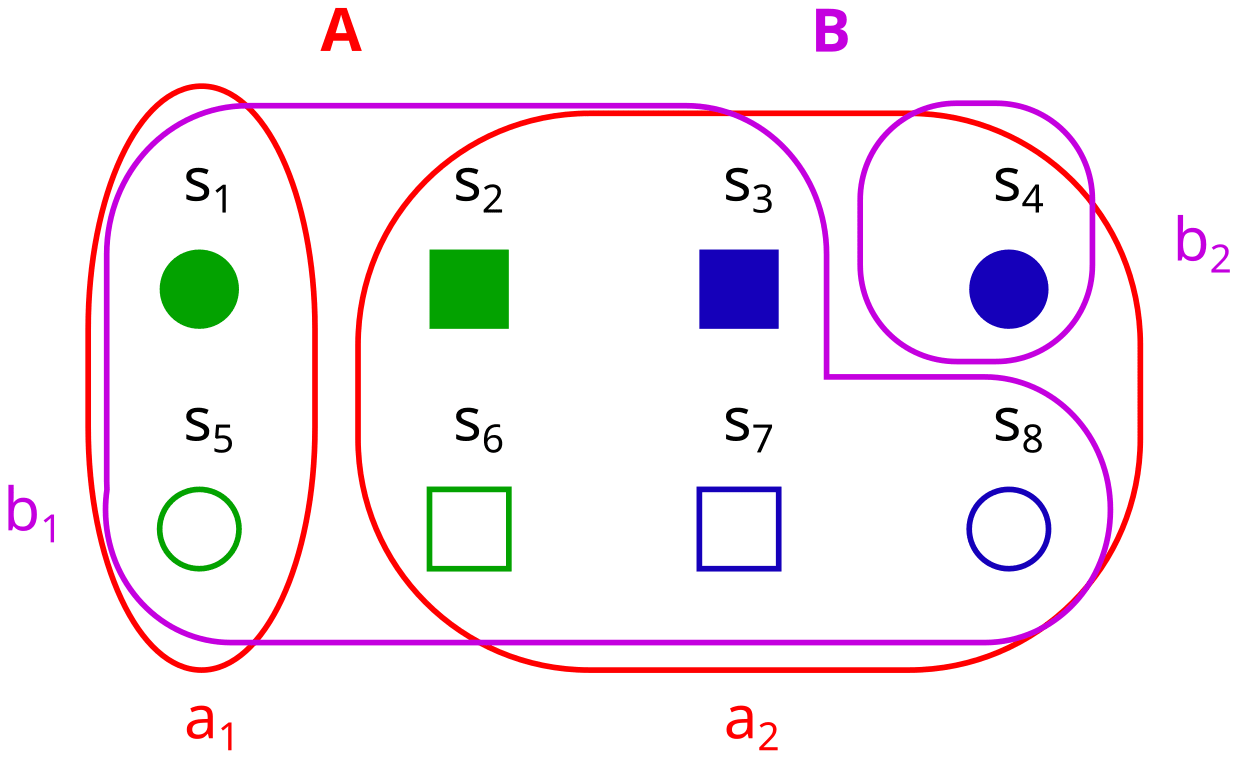
A is strictly before B! = {color, shape} and = {color, shape, fill}, so .
Now we have the building blocks to use factored sets for causal inference!
3. Causal Inference using Factored Sets
In this section I will walk through an example of inferring causality from data using factored sets.
Consider an experiment in which we collect 2 bits. The distribution P looks like this:
P(00) = 1%
P(01) = 9%
P(10) = 81%
P(11) = 9%
Let’s say X is the first bit, and Y is the second bit.
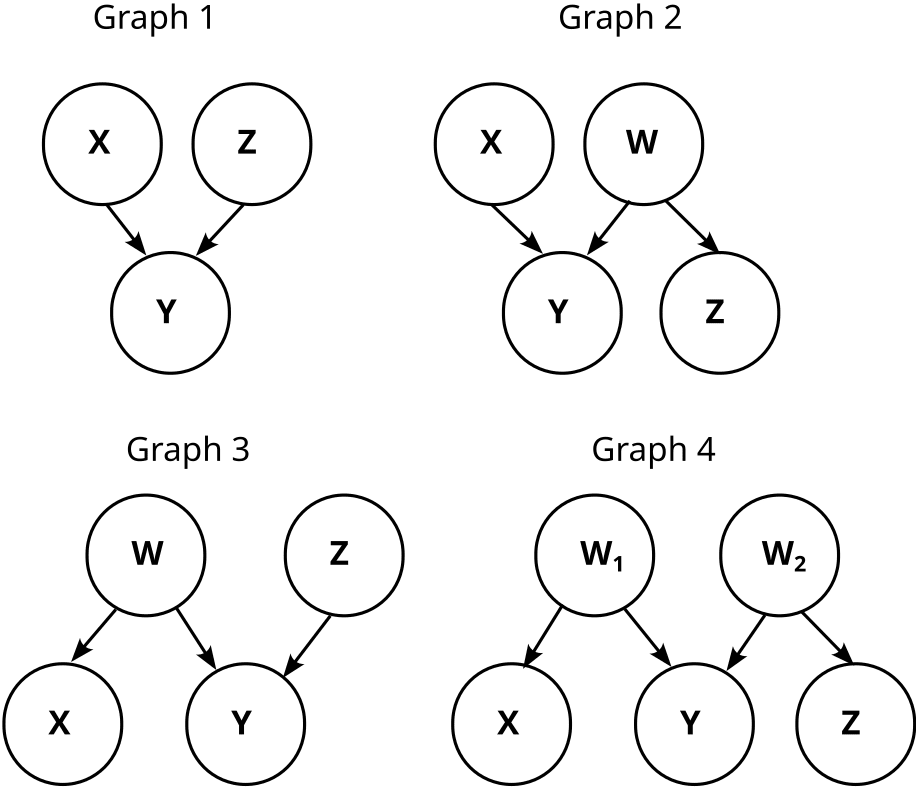
In the causal graph paradigm, we would observe that X and Y are dependent (). Thus we are not able to distinguish between these three causal graphs:
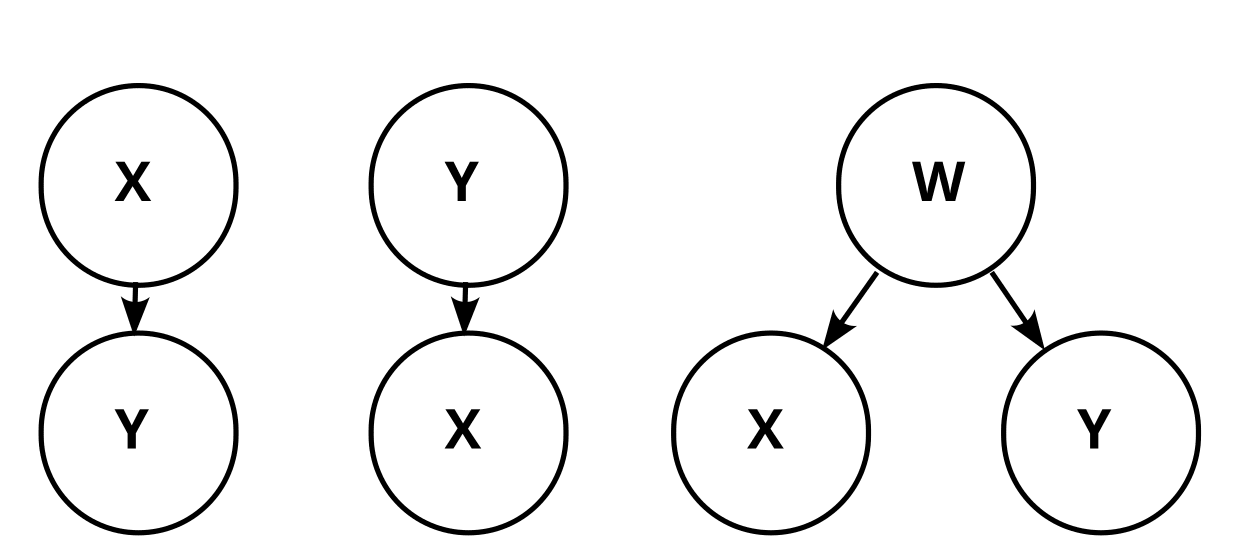
We don’t know whether X causes Y, Y causes X, or there is some common factor W that causes both.
How do we look at this in the Factored Set Paradigm?
In the factored set paradigm, start with the sample space of our distribution P:
We then say a model of the distribution is a factored set F = (S, B) and a function :
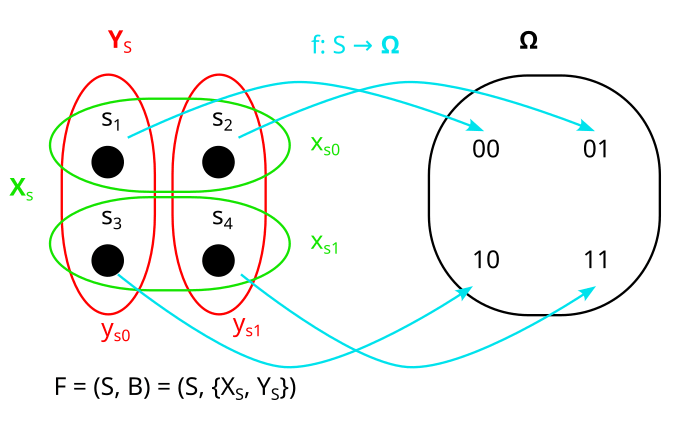
and are the “preimages” of X and Y under f. By that I mean that all their parts and are the preimages of and respectively, under f. That looks as follows:
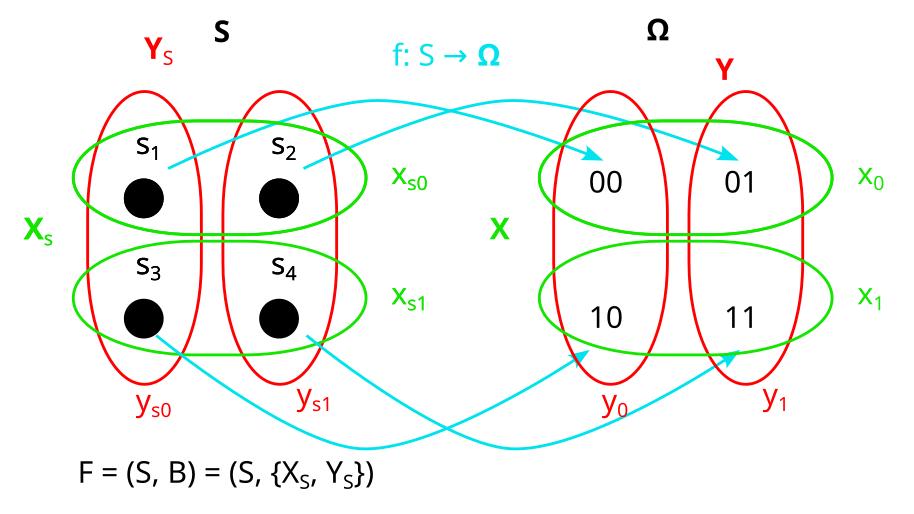
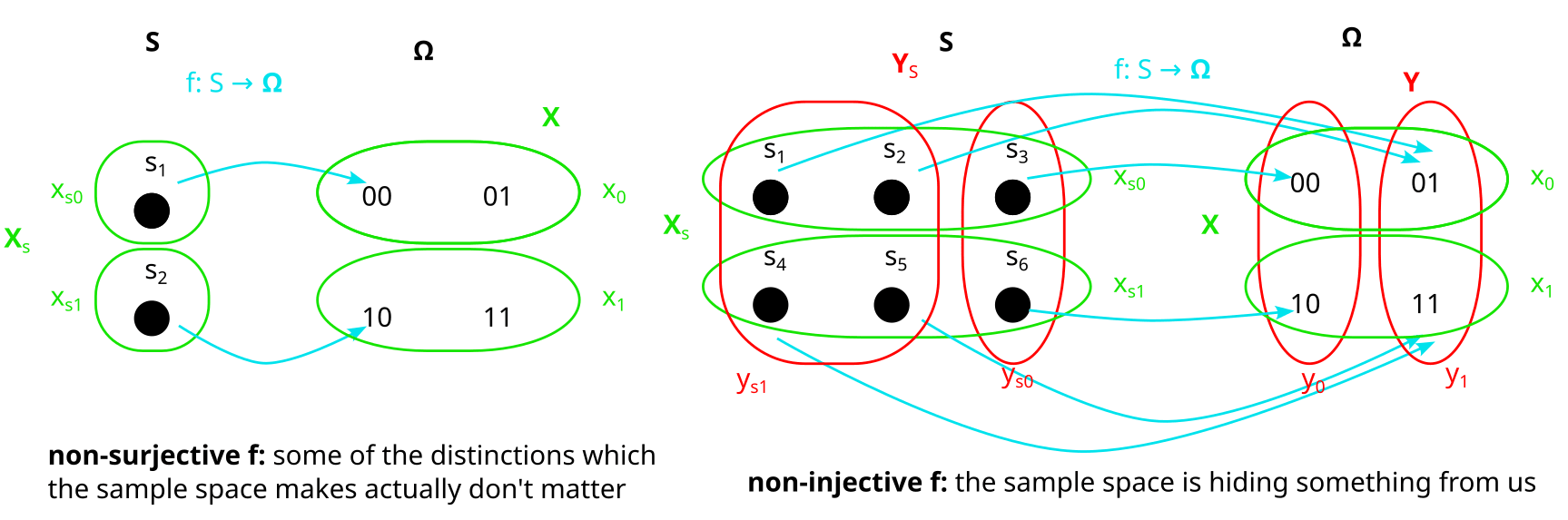
(Note that in this case f is bijective, but in general f does not have to be bijective. If we allow f to be non-bijective, then the framework works in more generality because we can describe some processes that we couldn’t otherwise describe. [3])
However, we can’t just use any factorization B. In order for (F, f) to count as a model of our distribution P, it needs to be such that the dependencies and independencies of our distribution are represented in the factorization.
That means:
- Two variables X and Y are independent in P if and only if and are orthogonal in F (i.e. their histories don’t overlap)
- Two variables X and Y are dependent in P if and only if and are not orthogonal in F
Remember, our probability distribution P was
P(00) = 1%
P(01) = 9%
P(10) = 81%
P(11) = 9%
Is the following actually a model of P?
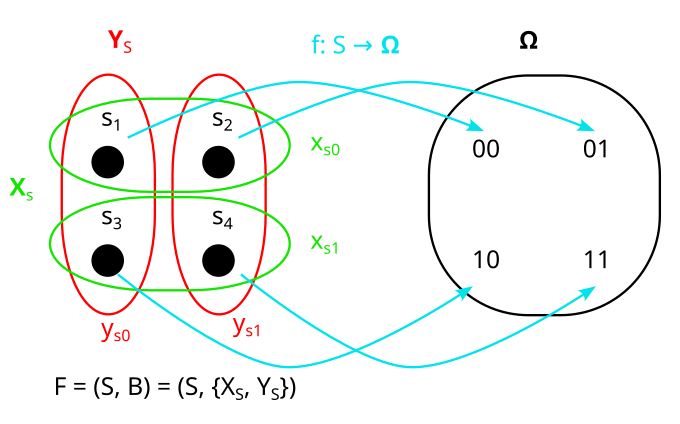
No, it is not: X, and Y are dependent in P, but and are orthogonal in F! (Note that orthogonality depends on what model we are in/what factorization we use.)
Here is a really tricky one: Is this a model of P?
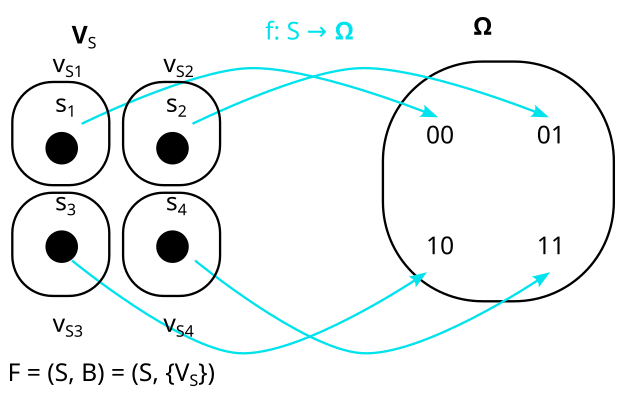
Also no, but this is hard to see, so let’s walk through it.
Consider the variable Z = X XOR Y
We don’t have to express our distribution in terms of X and Y, we can just as well define it in terms of X and Z. And then it looks like this:
P(00) = P(X=0, Z=0) = 1%
P(01) = P(X=0, Z=1) = 9%
P(10) = P(X=1, Z=1) = 81%
P(11) = P(X=1, Z=0) = 9%
We can see that Z and X are independent! (because, and also , and)
What does this mean for our model? It means that and need to be orthogonal.
Are and orthogonal in our model? Here it is again:
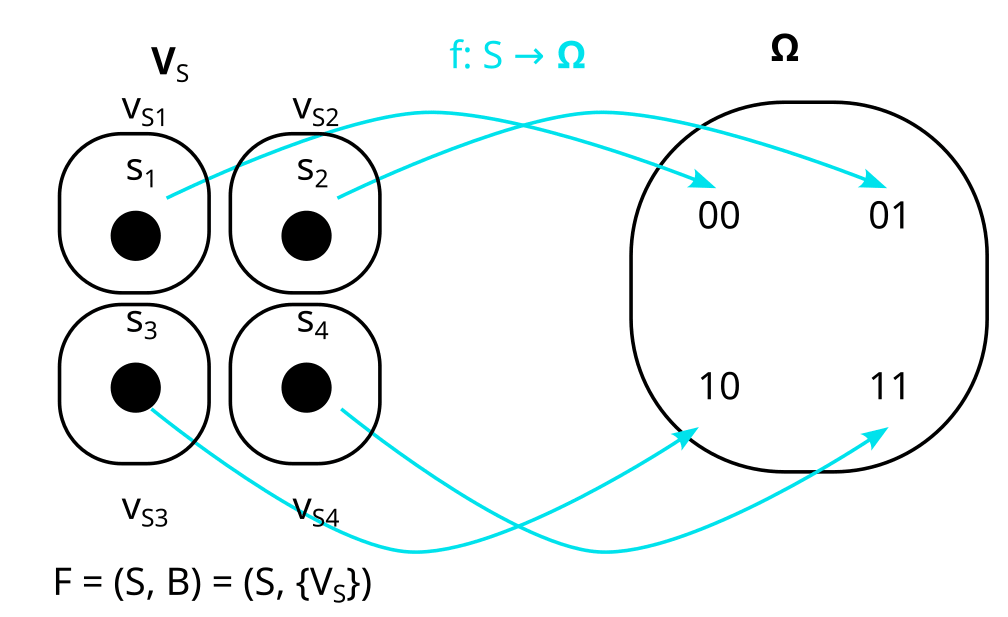
No, because the history for both and is {V}, so and have an overlapping history.
So F = (S, {}) is also not a model of P.
Does our distribution P have a model at all?
Yes - here is a model that actually works for P:
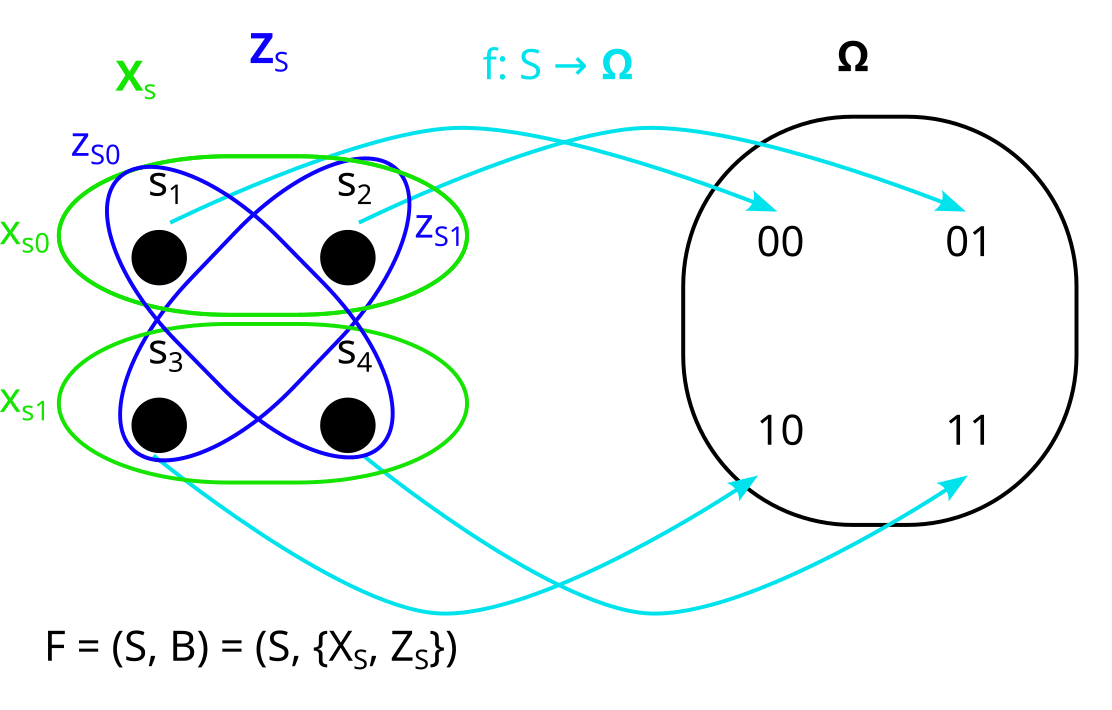
Here and = {}, and = {}.
This means and are orthogonal, which matches our observation that X and Z are independent in P. Also and are not orthogonal, which matches our observation that X and Y are dependent in P.
It also means that , so is strictly before .
If is strictly before , then the causal arrow goes from X to Y, so we have found a causal direction! It’s this one:
From what we know so far, this causal direction only holds for this particular model (F, f), but in fact, you can also prove that holds for any model of this distribution P.
So, we just inferred causality from observational (as opposed to interventional) data, in a way that Pearl’s causal models wouldn’t have inferred!
Sanity-checking the result in Pearl’s paradigm
I have encountered a lot of skepticism that we can infer the causality here. So I’m going to switch back to the Pearl paradigm, and explain why X causes Y if our distribution is P, and we can actually infer that from only observational data without needing interventional data.
This section will assume you know how to determine (in-)dependence in probability distributions and in causal graphs. (If you don’t, you can either just believe me, or learn about it here and here).
Again, say X is the first bit, Y is the second bit, and Z = X XOR Y. Here is our distribution again, in table-form:
| X | Y | Z | P(X, Y, Z) |
| 0 | 0 | 0 | 1% |
| 0 | 1 | 1 | 9% |
| 1 | 0 | 1 | 81% |
| 1 | 1 | 0 | 9% |
| Any other combination of X, Y, and Z | 0% | ||
The (in-)dependencies we can read from this are:
- X and Y are dependent
- X and Z are independent
- Y and Z are dependent
The possible causal graphs which fulfill these dependencies and independencies are these four:
So, we know that Y does not cause X! This matches our finite factored set finding that X causes Y, but it's weaker. Can we also infer that X causes Y?
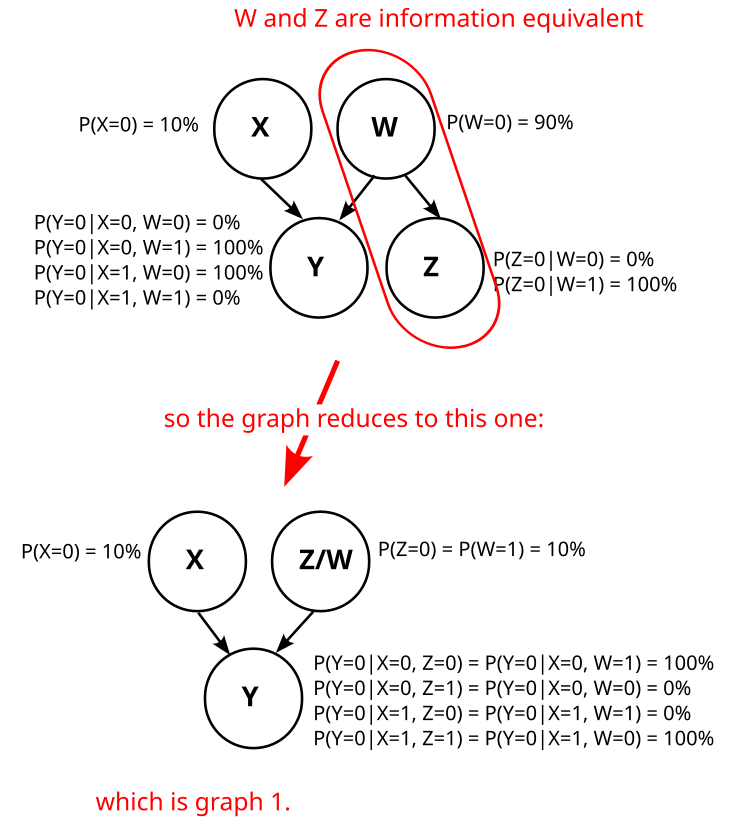
Let’s concretize the above graphs by adding the conditional probabilities. Graph 1 then looks like this:
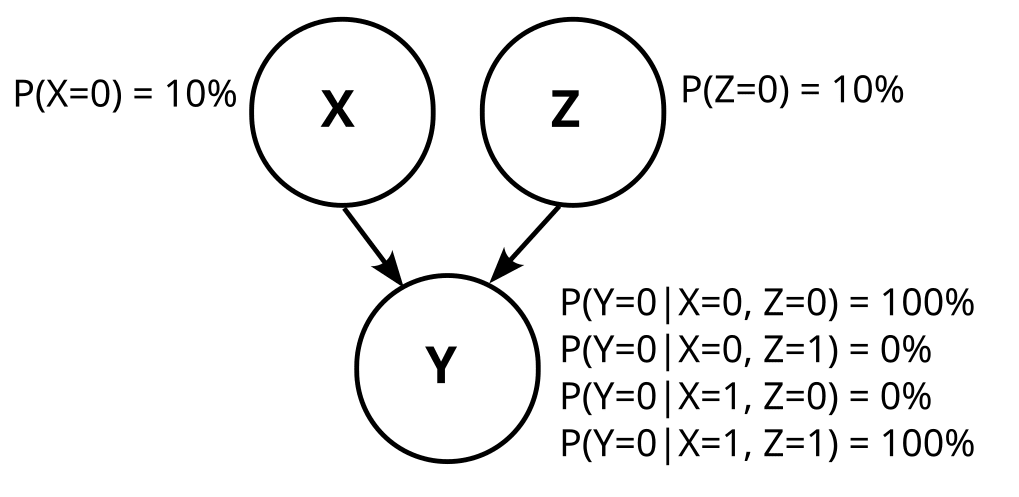
Graph 2 is somewhat trickier, because W is not uniquely determined. But one possibility is like this:
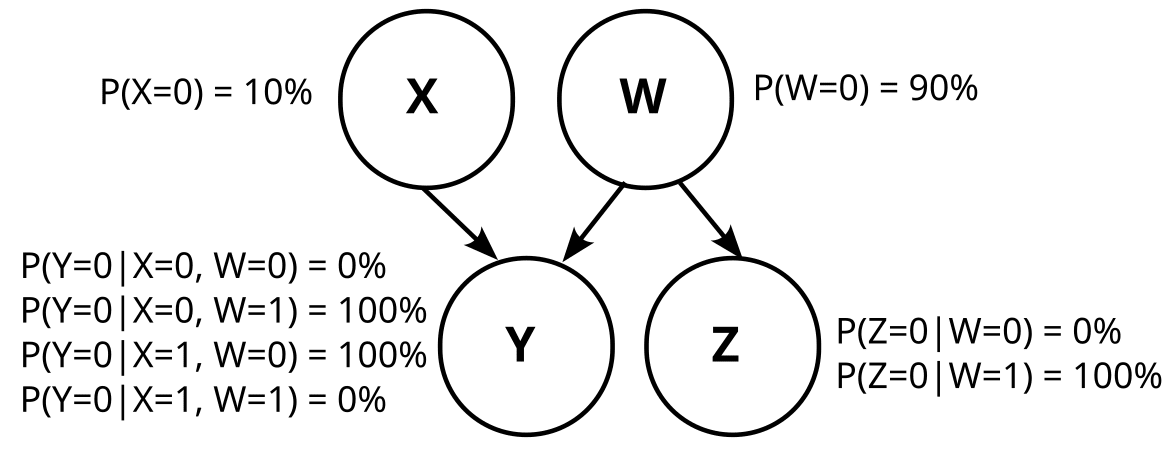
Note that W is just the negation of Z here (). Thus, W and Z are information equivalent, and that means graph 2 is actually just graph 1.
Can we find a different variable W such that graph 2 does not reduce to graph 1? I.e. can we find a variable W such that Z is not deterministic given W?
No, we can’t. To see that, consider the distribution . By definition of Z, we know that
.
In other words, is deterministic.
We also know that W d-separates Z from X,Y in graph 2:
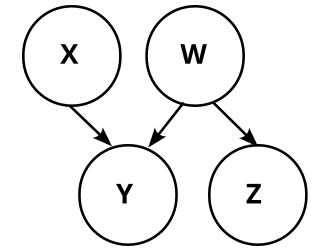
This d-separation implies that Z is independent from X, Z given W:
As is deterministic, also has to be deterministic.
So, graph 2 always reduces to graph 1, no matter how we choose W. Analogously, graph 3 and graph 4 also reduce to graph 1, and we know that our causal structure is graph 1:
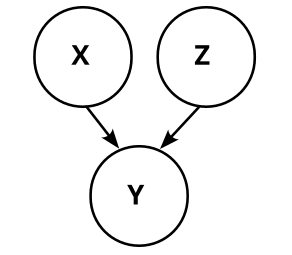
Which means we also know that X causes Y.
The reason why we usually wouldn’t have found this causal direction using causal graphs is that we wouldn’t even have considered Z as potentially interesting. This is what factored sets give us: They make us consider every possible way of defining variables, so we don’t miss out on any information that may be hidden if we just look at a predetermined set of variables.
Summary
Set factorizations are a way of expressing sets as a product of some factors, similar to how integer factorization is about expressing integers as a product of some factors.
We can define a history on them, that tells us which properties came “before” other properties. We say that two variables are orthogonal if they have no shared history. Using these notions of history and orthogonality, we can define a mathematical structure called model of a probability distribution. With this model, we can do causal inference (inferring causal structure from data).
Factored sets let us infer causal relations that we usually wouldn’t have found using causal graphs. For example, if we have two binary variables X and Y, and X is independent from X XOR Y, then we can infer the causal direction .
Further Reading
I hope you got a bit of a grasp on finite factored sets, and see why they are really neat. If you want to read more, the best entry point is probably this edited transcript from a talk by Scott Garrabrant.
For a non-mathematical intuition how Scott relates the concepts of time, causality, abstraction, and agency, see his Saving Time post.
I haven’t looked closely into AI alignment specific applications of factored sets, but it looks like they can be used to better talk about embedded agency, decision theory, and ELK.
_____
This post is a result of a distillation workshop led by John Wentworth at SERI MATS. I’d like to thank Leon Lang, Scott Garrabrant, Matt MacDermott, Jesse Hoogland, and Marius Hobbhahn for feedback and discussions on this post.
- ^
Note that the number of set factorizations of an n-element set is not the same as the number of integer factorizations of n, because elements are distinguishable, so for example these two factorizations do not count as the same factorization:
- ^
Actually, it’s somewhat more complicated than “X and Y are (conditionally) orthogonal if and only if they are independent”. The full version is more like “If and are partitions on a set S, which has a mapping to the sample space, then and are (conditionally) orthogonal if and only if the images X and Y of and are (conditionally) independent”. But for the sake of this explanation, if you just remember that “orthogonality independence”, that's enough.
- ^
Even if f is not bijective, the “preimages” and of X and Y are always well-defined partitions. Here are two examples in which f is not bijective: