This post has been recorded as part of the LessWrong Curated Podcast, and can be listened to on Spotify, Apple Podcasts, and Libsyn.
This is Part 1 of my «Boundaries» Sequence on LessWrong.
Summary: «Boundaries» are a missing concept from the axioms of game theory and bargaining theory, which might help pin down certain features of multi-agent rationality (this post), and have broader implications for effective altruism discourse and x-risk (future posts).
1. Boundaries (of living systems)
Epistemic status: me describing what I mean.
With the exception of some relatively recent and isolated pockets of research on embedded agency (e.g., Orseau & Ring, 2012; Garrabrant & Demsky, 2018), most attempts at formal descriptions of living rational agents — especially utility-theoretic descriptions — are missing the idea that living systems require and maintain boundaries.
When I say boundary, I don't just mean an arbitrary constraint or social norm. I mean something that could also be called a membrane in a generalized sense, i.e., a layer of stuff-of-some-kind that physically or cognitively separates a living system from its environment, that 'carves reality at the joints' in a way that isn't an entirely subjective judgement of the living system itself. Here are some examples that I hope will convey my meaning:
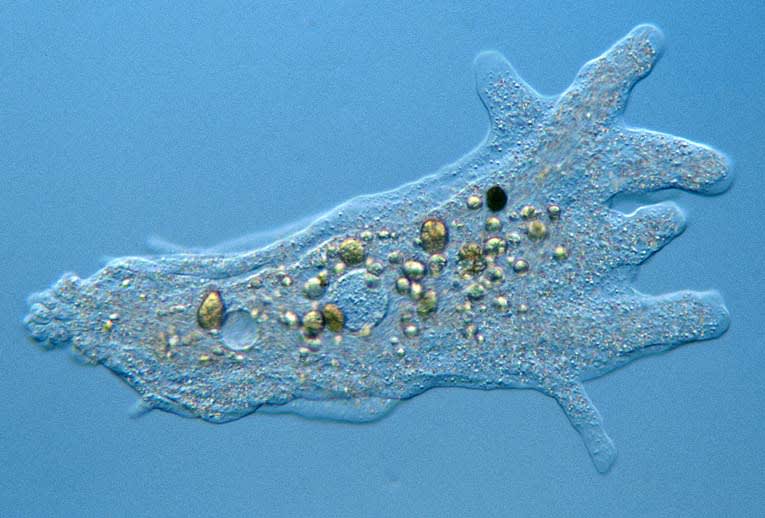
- a cell membrane (separates the inside of a cell from the outside);
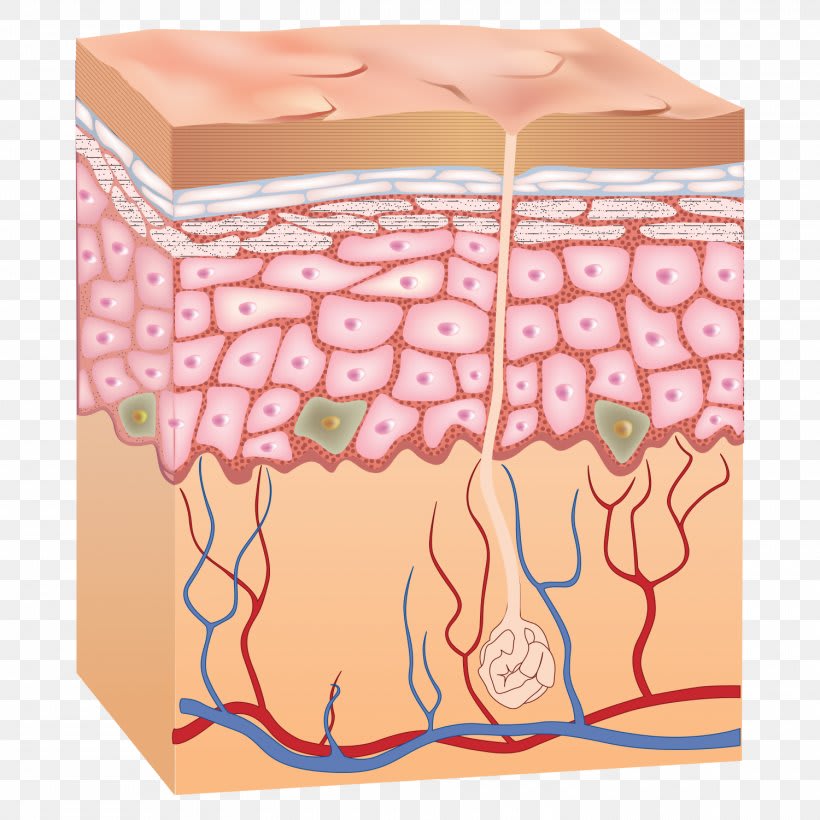
- a person's skin (separates the inside of their body from the outside);
- a fence around a family's yard (separates the family's place of living-together from neighbors and others);
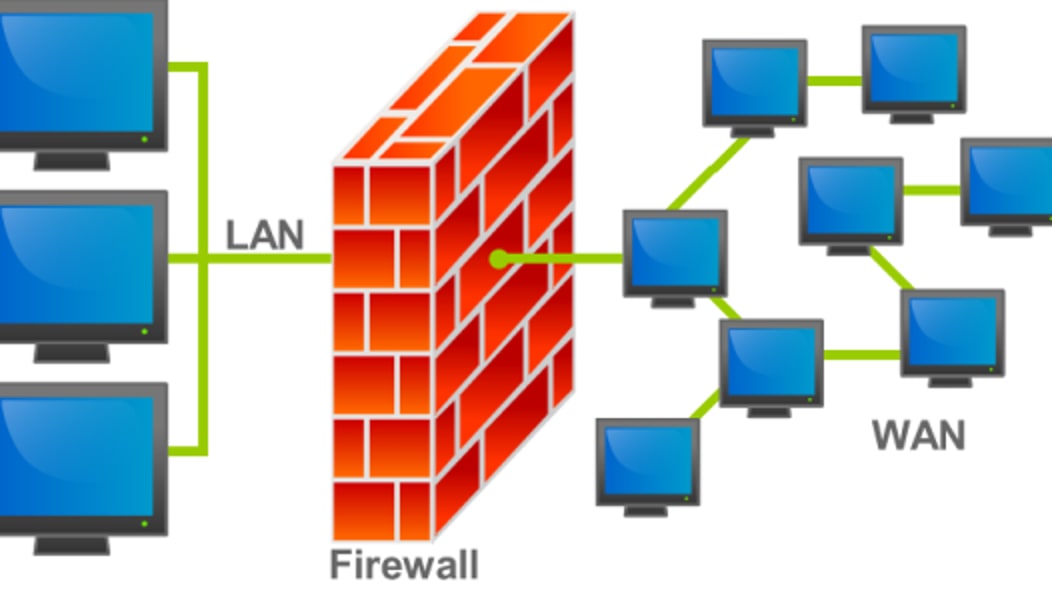
- a digital firewall around a local area network (separates the LAN and its users from the rest of the internet);
- a sustained disassociation of social groups (separates the two groups from each other)
- a national border (separates a state from neighboring states or international waters).
 |  |
 |  |
 | 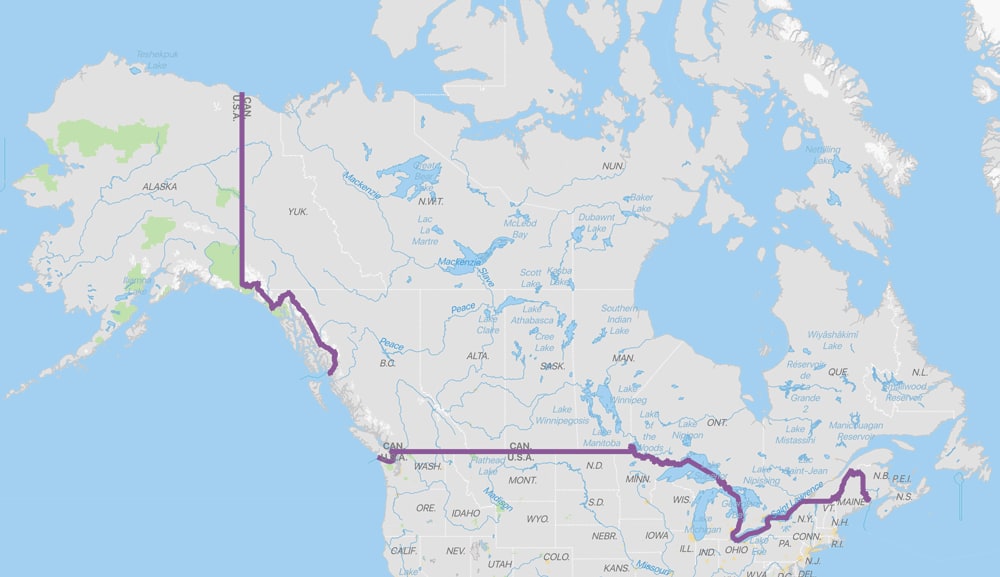 |
| Figure 1: Cell membranes, skin, fences, firewalls, group divisions, and state borders as living system boundaries. | |
Comparison to Cartesian Boundaries.
For those who'd like a comparison to 'Cartesian boundaries', as in Scott Garrabrant's Cartesian Frames work, I think what I mean here is almost exactly the same concept. The main differences are these:
- (life-focus) I want to focus on boundaries of things that might naturally be called "living systems" but that might not broadly be considered "agents", such as a human being that isn't behaving very agentically, or a country whose government is in a state of internal disagreement. (I thought of entitling this sequence "membranes" instead, but stuck with 'boundaries' because of the social norm connotation.)
- (flexibility-focus) Also, the theory of Cartesian Frames assumes a fixed cartesian boundary for the agent, rather than modeling the boundary as potentially flexible, pliable, or permeable over time (although it could be extended to model that).
Comparison to social norms.
Certain social norms exist to maintain separations between livings systems. For instance:
- Personal space boundaries. Consider a person Alex who wants to give his boss a hug, in a culture with a norm against touching others without their consent. In that case, the boss's personal space creates a kind of boundary separating the boss from Alex, and there's a protocol — asking permission — that Alex is expected to follow before crossing the boundary.
- Information boundaries for groups. Consider a person Betty who's having a very satisfying romantic relationship, in a culture where there's a norm of not discussing romantic relationships with colleagues at work. In that case, Alice maintains an information boundary between the details of her romantic life and her workplace. The workplace is kind of living system comprising multiple people and conventions for their interaction, and it's being protected from information about Alice's romantic relationships.
- Information boundaries for individuals. Consider a person Cory who has violent thoughts about his friends, in a culture where there's a norm that you shouldn't tell people if you're having violent thoughts about them. In that case, if Cory is thinking about punching David, Cory is expected not to express that thought, as away of protecting David from the influence of the sense of physical threat David would feel and react to if Cory expressed it. In this case, Cory maintains a kind of information boundary around the part of Cory's mind with the violent thoughts, which may be viewed either as enclosing the violent parts of Cory's mind, or as enclosing and protecting the rest of the word outside it.
2. Canonical disagreement points as missing from utility theory and game theory
Epistemic status: uncontroversial overview and explanation of well-established research.
Game theory usually represents players as having utility functions (payoff functions), and often tries to view the outcome of the game as arising as a consequence of the players' utilities. However, for any given concept of "equilibrium" attempting to predict how players will behave, there are often many possible equilibria. In fact, there are a number of theorems in game theory called "folk theorems" (reference: Wikipedia) that show very large spaces of possible equilibria result when games have certain features approximating real-world interaction, such as
- the potential for players to talk to each other and make commitments (Kalai et al, 2010)
- the potential for players to interact repeatedly and thus establish "reputations" with each other (source: Wikipedia).
Here's a nice illustration of a folk theorem from a Chegg.com homework set:
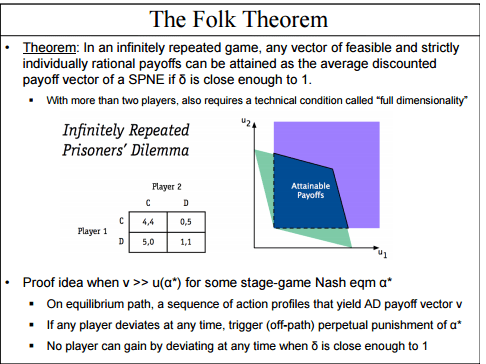
The zillions of possible equilibria arising from repeated interactions leave us with not much of a prediction about what will actually happen in a real-world game, and not much of a normative prescription of what should happen, either.
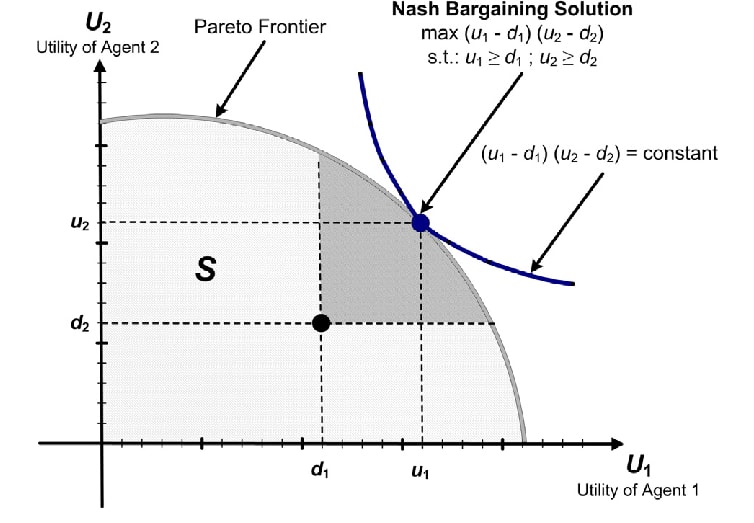
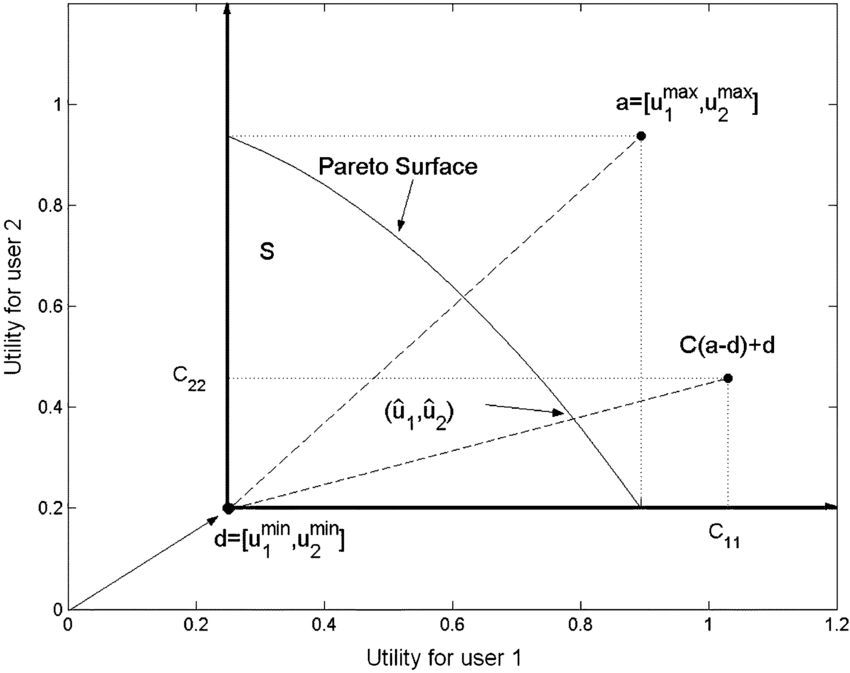
Bargaining theory attempts to predict and/or prescribe how agents end up "choosing an equilibrium", usually by writing down some axioms to pick out a special point on the Pareto frontier of possible, such as the Nash Bargaining Solution and Kalai-Smordinsky Bargaining Solution (reference: Wikipedia). It's not crucial to understand these figures for the remainder of the post, but if you don't, I do think think it's worth learning about them sometime, starting with the Wikipedia article:
simage source: Karmperis et al, 2013; to learn more, see Wikipedia)
(image source: Borgstrom et al, 2007; to learn more, start with Wikipedia)
The main thing to note about the above bargaining solutions is that they both depend on the existence of a constant point d, called a "disagreement point", representing a pair of constant utility levels that each player will fall back on attaining if the process of negotiation breaks down.
(See also this concurrently written recent LessWrong post about Kalai & Kalai's cooperative/competitive 'coco' bargaining solution. The coco solution doesn't assume a constant disagreement point, but it does assume transferrable utility, which has its own problems, due to difficulties with defining interpersonal comparisons of utility [source: lots].)
The utility achieved by a player at the disagreement point is sometimes called their best alternative to negotiated agreement (BATNA):
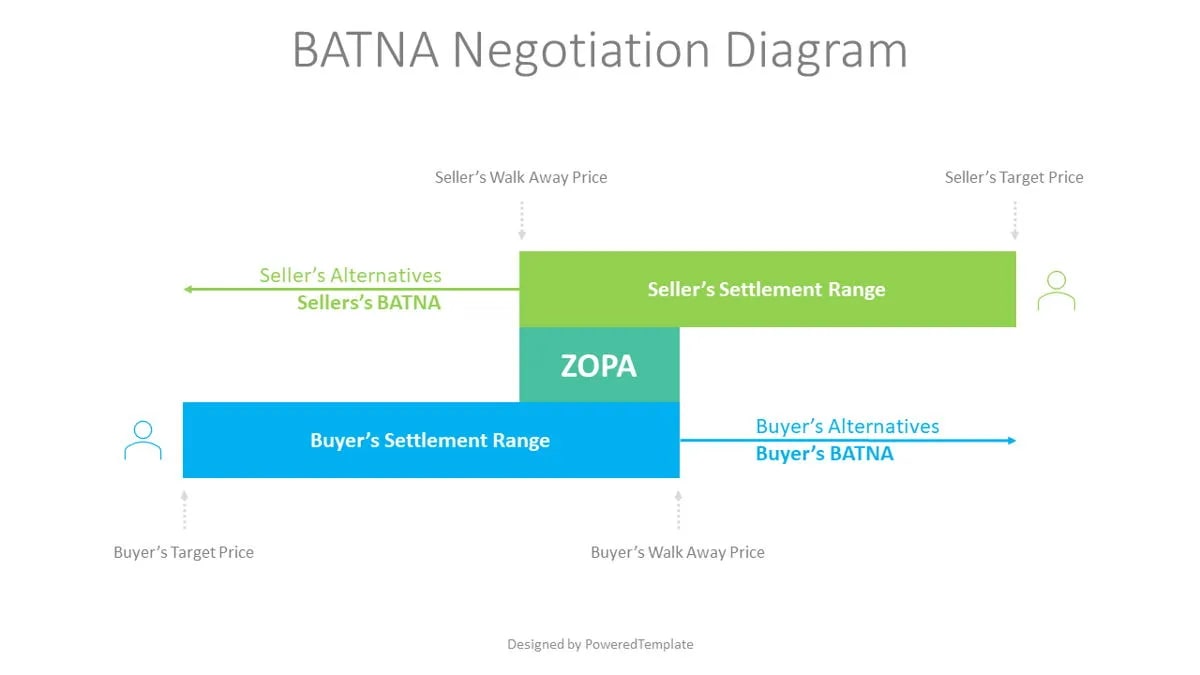
(source: PoweredTemplate.com ... not very academic, but a good illustration!)
Within the game, the disagreement point, i.e., the pair of BATNAs, may be viewed as defining what "zero" (marginal) utility means for each player.
(Why does zero need a definition, you might ask? Recall that the most broadly accepted axioms for the utility-theoretic foundations of game theory — namely, the von Neumann–Morgenstern rationality axioms [reference: Wikipedia]) — only determine a player's utility function modulo a positive affine transformation (). So, in the wild, there's no canonical way to look at an agent and say what is or isn't a zero-utility outcome for that agent.)
While it's appealing to think in terms of BATNAs, in physical reality, payoffs outside of negotiations can depend very much on the players' behavior inside the negotiations, and thus is not a constant. Nash himself wrote about this limitation (Nash, 1953) just three years after originally proposing the Nash bargaining solution. For instance, if someone makes an unacceptable threat against you during a business negotiation, you might go to the police and have them arrested, versus just going home and minding your business if the negotiations had failed in a more normal/acceptable way. In other words, you have the ability to control their payoff outside the negotiation, based on what you observe during the negotiation. It's not a constant; you can affect it.
So, the disagreement point or BATNA concept isn't really applicable on its own, unless something is protecting the BATNA from what happens in the negotiation, making it effectively constant. Basically, the two players need a safe/protected/stable place to walk away to in order for a constant "walk away price" to be meaningful. For many people in many situations, that place is their home:

(source: owned)
Thus, to the extent that we maintain social norms like "mind your own business" and "don't threaten to attack people" and "people can do whatever they want in the privacy of their own homes", we also simplify bargaining dynamics outside the home, by maintaining a well-defined fallback option for each person (a disagreement point), of the form "go home and do your own thing".
3. Boundaries as a way to select disagreement points in bargaining
Epistemic status: research ideas, both for pinning down technical bargaining solutions, and for fixing game theory to be more applicable to real-life geopolitics and human interactions.
Since BATNAs need protection in order to be meaningful in negotiations, to identify BATNAs, we must ask: what protections already exist, going into the negotiation?
For instance,
- Is there already a physically identifiable boundary or membrane separating each agent from the other or its environment? Is it physically strong? If yes, it offers a kind of BATNA: the organisms can simply disengage and focus on applying their resources inside the membrane (e.g., 'taking your ball and going home'). If not,
- Is there an existing social convention for protecting the membrane? If so, it offers a kind of BATNA. If not,
- Would the agents have decided behind a veil of ignorance that they will respect each other's membranes/boundaries, before entering negotiations/interaction? If so, the agents might have already acausally agreed upon a social convention to protect the membranes.
4. Some really important boundaries
In real-world high-stakes negotiations between states — wars — almost the whole interaction is characterized by
- a violation of an existing boundary (e.g., "an attack on American soil"), or threat or potential threat of such a violation, and/or
- what new boundaries, if any, will exist after the violation or negotiation (re-defining territories of the respective nations).
Source: Britannica for kids ... again, not very academic, but nicely evocative of states changing their boundaries.
Finally, the issue of whether AI technology will cause human extinction is very much an issue of whether certain boundaries can be respected and maintained, such as the boundaries of the human body and mind that protect individuals, as well as boundaries around physical territories and cyberspace that (should) protect human civilization.
That, however, will be a topic of a future post. For now, the main take-aways I'd like to re-iterate are that boundaries of living systems are important, and that they have a technical role to play in the theory and practice of how agents interact, including in formal descriptions of how one or more agents will or should reach agreements in cases of conflict.
In the next post, I'll talk more about how that concept of boundaries could be better integrated into discourse on effective altruism.
5. Summary
In this post, I laid out what I mean by boundaries (of living systems), I described how a canonical choice of a "zero point" or "disagreement point" is missing from utility theory and bargaining theory, I proposed that living system boundaries have a role to play in defining those disagreement points, and I briefly alluded to the importance of boundaries in navigating existential risk.
This was Part 1 of my «Boundaries» Sequence.