Review of "Fun with +12 OOMs of Compute"
12Daniel Kokotajlo
3adamShimi
4Daniel Kokotajlo
3adamShimi
5Daniel Kokotajlo
3adamShimi
2Joe Collman
2Daniel Kokotajlo
6Joe Collman
3Daniel Kokotajlo
3Joe Collman
4Daniel Kokotajlo
4Joe Collman
3Daniel Kokotajlo
3Joe Collman
3Daniel Kokotajlo
3Joe Collman
2Daniel Kokotajlo
6Sammy Martin
5Daniel Kokotajlo
1Raemon
New Comment
Thanks for doing this! I'm honored that you chose my post to review and appreciate all the thought you put into this.
I have one big objection: The thing you think this post assumes, this post does not actually assume. In fact, I don't even believe it! In more detail:
You say:
The relevance of this work appears to rely mostly on the hypothesis that the +12 OOMs of magnitude of compute and all relevant resources could plausibly be obtained in a short time frame. If not, then the arguments made by Daniel wouldn’t have the consequence of making people have shorter timelines.
I disagree. This post works within Ajeya's framework, which works as follows: First, we come up with a distribution over how much extra compute we'd need given 2020's levels of knowledge. Then, we come up with projections for how knowledge will improve over time, and how compute will increase over time. Then we combine all three to get our timelines. (Compute increasing can be thought of as moving us rightward through the distribution, and knowledge improving can be thought of as shifting the entire distribution leftward.)
Ajeya's distribution has its median at +12 OOMs. This corresponds to answering "50%" to my Question Two. If you instead answer something higher, then you (all else equal) must have shorter timelines, because you put more mass in the lower region. Now, you could put all that extra mass in, say, the region from +9 to +12 OOMs, and in that case your credence in short timelines wouldn't go up, because in the short term we aren't going to cross more than (say) 6 OOMs. This is why I had the "all else equal" qualifier. If your distribution over the next 12 OOMs looks like Ajeya's except that it totals to 80% instead of 50%, then (I calculate) the median of your AI timelines should be somewhere in the late 2030's.
To put it another way: I don't actually believe we will get to +12 OOMs of compute, or anywhere close, anytime soon. Instead, I think that if we had +12 OOMs, we would very likely get TAI very quickly, and then I infer from that fact that the probability of getting TAI in the next 6 OOMs is higher than it would otherwise be (if I thought that +12 OOMs probably wasn't enough, then my credence in the next 6 OOMs would be correspondingly lower).
To some extent this reply also partly addresses the concerns you raised about memory and bandwidth--I'm not actually saying that we actually will scale that much; I'm using what would happen if we magically did as an argument for what we should expect if we (non-magically) scale a smaller amount.
You're welcome!
To put it another way: I don't actually believe we will get to +12 OOMs of compute, or anywhere close, anytime soon. Instead, I think that if we had +12 OOMs, we would very likely get TAI very quickly, and then I infer from that fact that the probability of getting TAI in the next 6 OOMs is higher than it would otherwise be (if I thought that +12 OOMs probably wasn't enough, then my credence in the next 6 OOMs would be correspondingly lower).
To some extent this reply also partly addresses the concerns you raised about memory and bandwidth--I'm not actually saying that we actually will scale that much; I'm using what would happen if we magically did as an argument for what we should expect if we (non-magically) scale a smaller amount.
(Talking only for myself here)
Rereading your post after seeing this comment:
What I’ve done in this post is present an intuition pump, a thought experiment that might elicit in the reader (as it does in me) the sense that the probability distribution should have the bulk of its mass by the 10^35 mark.
I personally misread this, and understood "the bulk of its mass at the 10^35 mark". The correct reading is more in line with what you're saying here. That's probably a reason why I personnally focused on the +12 OOMs mark (I mean, that's also in the title).
So I agree we misunderstood some parts of your post, but I still think our issue remains. Except that instead of being about justifying +12 OOMs of magnitude in the short term, it becomes about justifying why the +12 OOMs examples should have any impact on, let's say, +6 OOMs.
I personally don't feel like your examples give me an argument for anywhere but the +12 OOMs mark. That's where they live, and those examples seem to require that much compute, or still a pretty big amount of it. So reading your post makes me feel like I should have more probability mass at this mark or very close to it, but I don't see any reason to update the probability at the +6OOMs mark say.
And if the +12 OOMs looks really far, as it does in my point of view, then that definitely doesn't make me update towards shorter timelines.
Thanks! Well, I agree that I didn't really do anything in my post to say how the "within 12 OOMs" credence should be distributed. I just said: If you distribute it like Ajeya does except that it totals to 80% instead of 50%, you should have short timelines.
There's a lot I could say about why I think within 6 OOMs should have significant probability mass (in fact, I think it should have about as much mass as the 7-12 OOM range). But for now I'll just say this: If you agree with me re Question Two, and put (say) 80%+ probability mass by +12 OOMs, but you also disagree with me about what the next 6 OOMs should look like and think that it is (say) only 20%, then that means your distribution must look something like this:
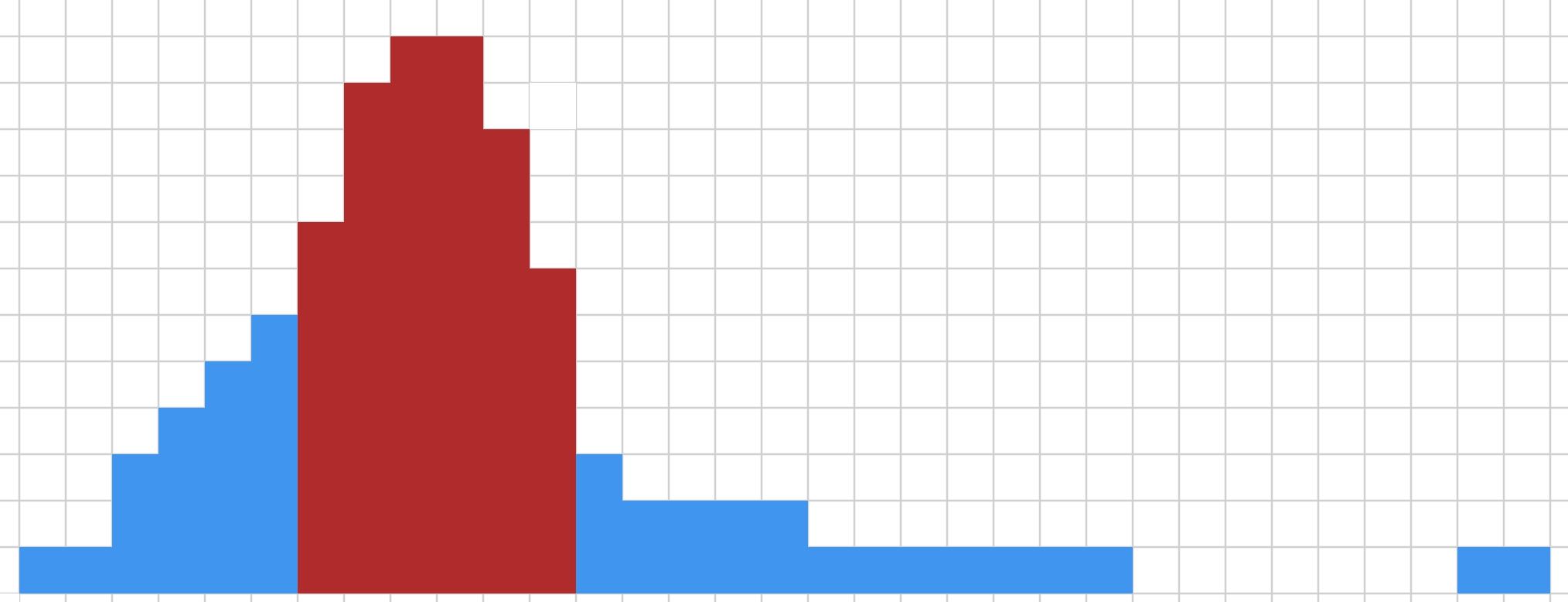
EDIT to explain: Each square on this graph is a point of probability mass. The far-left square represents 1% credence in the hypothesis "It'll take 1 more OOM." The second-from the left represents "It'll take 2 more OOM." The third-from-the-left is a 3% chance it'll take 3 more OOM, and so on. The red region is the region containing the 7-12 OOM hypotheses.
Note that I'm trying to be as charitable as I can when drawing this! I only put 2% mass on the far right (representing "not even recapitulating evolution would work!"). This is what I think the probability distribution of someone who answered 80% to my Question Two should look like if they really really don't want to believe in short timelines. Even on this distribution, there's a 20% chance of 6 or fewer OOMs being enough given current ideas/algorithms/etc. (And hence, about a 20% chance of AGI/TAI/etc. by 2030, depending on how fast you think we'll scale up and how much algorithmic progress we'll make.)
And even this distribution looks pretty silly to me. Like, why is it so much more confident that 11 OOMs will be how much we need, than 13 OOMs? Given our current state of ignorance about AI, I think the slope should not be that steep.
Let me try to make an analogy with your argument.
Say we want to make X. What you're saying is "with 10^12 dollars, we could do it that way". Why on earth would I update at all whether it can be done with 10^6 dollars? If your scenario works with that amount, then you should have described it using only that much money. If it doesn't, then you're not providing evidence for the cheaper case.
Similarly here, if someone starts with a low credence on prosaic AGI, I can see how your arguments would make them put a bunch of probability mass close to +10^12 compute. But they have no reason to put probability mass anywhere far from that point, since the scenarios you give are tailored to that. And lacking an argument for why you can get that much compute in a short timeline, then they probably end up thinking that if prosaic AGI ever happens, it's probably after every other option. Which seems like the opposite of the point you're trying to make.
I'm not sure, but I think that's not how updating works? If you have a bunch of hypotheses (e.g. "It'll take 1 more OOM," "It'll take 2 more OOMs," etc.) and you learn that some of them are false or unlikely (only 10% chance of it taking more than 12" then you should redistribute the mass over all your remaining hypotheses, preserving their relative strengths. And yes I have the same intuition about analogical arguments too. For example, let's say you overhear me talking about a bridge being built near my hometown, and you wonder how many tons of steel it will cost. You don't know much about bridge construction so your uncertainty ranges over several orders of magnitude -- say, from 10^2 to 10^9 tons. Then you do some googling and discover that 450,000 tons is how much it took to build the longest bridge in the world. OK, so clearly it almost certainly won't take more than 10^5 tons to build the bridge being built near my hometown. What do you do with all the probability mass you used to have above 10^5? Do you pile it all up on 10^4 and 10^5? No, you redistribute it evenly. You DO come to have a higher credence that it will be merely 10^2 or 10^3 as a result of learning about the longest bridge in the world, because you are Bayesian and you are deleting falsified hypotheses and renormalizing.
Of course, real life updates are never that simple, because they involve more information than the pure "it won't be more than X." For example, the fact that I chose to write about 12 OOMs instead of 6 should be suspicious; it's evidence that 6 OOMs isn't enough (otherwise I would have chosen to write about 6, right?). Also, the stuff I said about what you could do with 12 OOMs may have also contained information about what you can't do with 6 -- for example, my calculations for Crystal Nights probably also serve as evidence that an only-6-OOM version of Crystal Nights wouldn't work. You probably didn't think it would, but if you did, then reading my Crystal Nights thing may have convinced you it wouldn't.
To the first suspicion I'll say: I had good reasons for writing about 12 rather than 6 which I am happy to tell you about if you like. To the second I'll say: YMMV, but it doesn't feel to me that the scenarios I sketched at 12 OOMs provide much evidence either way about what happens at 6 OOMs. It feels to me that they really can be mostly characterized as providing evidence that it won't take more than 12.
...
Independently of the above though, what do you think about my graph-based argument? In a sentence, the argument is: If you answer 80% to Question Two but still have <20% credence in TAIby2030, your distribution must look at least as spiky and steep as the red-blue one I sketched, but that's implausible because overconfident--it seems unjustified to have so much more credence in +11 OOMs than in +13.
...
Independently of the above, I'm happy to provide more inside-view reasons to take "within 6 OOMs" seriously. It just wasn't the focus of the post. You might be right that it should have been the focus of the post--but like I said, I had reasons.
About the update
You're right, that's what would happen with an update.
I think that the model I have in mind (although I hadn't explicitly thought about it until know), is something like a distribution over ways to reach TAI (capturing how probable it is that they're the first way to reach AGI), and each option comes with its own distribution (let's say over years). Obviously you can compress that into a single distribution over years, but then you lose the ability to do fine grained updating.
For example, I imagine that someone with relatively low probability that prosaic AGI will be the first to reach AGI, upon reading your post, would have reasons to update the distribution for prosaic AGI in the way you discuss, but not to update the probability that prosaic AGI will be the first to reach TAI. On the other hand, if there was a argument centered more around an amount of compute we could plausibly get in a short timeframe (the kind of thing we discuss as potential follow-up work), then I'd expect that this same person, if convinced, would put more probability that prosaic AGI will be the first to reach TAI.
Graph-based argument
I must admit that I have trouble reading your graph because there's no scale (although I expect the spiky part is centered at +12 OOMs? As for the textual argument, I actually think it makes sense to put quite low probability to +13 OOMs if one agrees with your scenario.
Maybe my argument is a bit weird, but it goes something like this: based on your scenarios, it should be almost sure that we can reach TAI with +12 OOMs of magnitude. If it's not the case, then there's something fundamentally difficult about reaching TAI with prosaic AGI (because you're basically throwing all the compute we want at it), and so I expect very little probability of a gain from 1 OOMs.
The part about this reasoning that feels weird is that I reason about 13 OOMs based on what happens at 12 OOMs, and the idea that we care about 13 OOMs iff 12 OOMs is not enough. It might be completely wrong.
Reasons for 12 OOMs
To the first suspicion I'll say: I had good reasons for writing about 12 rather than 6 which I am happy to tell you about if you like.
I'm both interested, and (without knowing them), I expect that I will want you to have put them in the post, to deal with the implicit conclusion that you couldn't argue 6 OOMs.
Also interested by your arguments for 6 OOMs or pointers.
If you have a bunch of hypotheses (e.g. "It'll take 1 more OOM," "It'll take 2 more OOMs," etc.) and you learn that some of them are false or unlikely (only 10% chance of it taking more than 12" then you should redistribute the mass over all your remaining hypotheses, preserving their relative strengths.
This depends on the mechanism by which you assigned the mass initially - in particular, whether it's absolute or relative. If you start out with specific absolute probability estimates as the strongest evidence for some hypotheses, then you can't just renormalise when you falsify others.
E.g. consider we start out with these beliefs:
If [approach X] is viable, TAI will take at most 5 OOM; 20% chance [approach X] is viable.
If [approach X] isn't viable, 0.1% chance TAI will take at most 5 OOM.
30% chance TAI will take at least 13 OOM.
We now get this new information:
There's a 95% chance [approach Y] is viable; if [approach Y] is viable TAI will take at most 12 OOM.
We now need to reassign most of the 30% mass we have on >13 OOM, but we can't simply renormalise: we haven't (necessarily) gained any information on the viability of [approach X].
Our post-update [TAI <= 5OOM] credence should remain almost exactly 20%. Increasing it to ~26% would not make any sense.
For AI timelines, we may well have some concrete, inside-view reasons to put absolute probabilities on contributing factors to short timelines (even without new breakthroughs we may put absolute numbers on statements of the form "[this kind of thing] scales/generalises"). These probabilities shouldn't necessarily be increased when we learn something giving evidence about other scenarios. (the probability of a short timeline should change, but in general not proportionately)
Perhaps if you're getting most of your initial distribution from a more outside-view perspective, then you're right.
We now need to reassign most of the 30% mass we have on >13 OOM, but we can't simply renormalise: we haven't (necessarily) gained any information on the viability of [approach X].
Our post-update [TAI <= 5OOM] credence should remain almost exactly 20%. Increasing it to ~26% would not make any sense.
I don't see why this is. From a bayesian perspective, alternative hypotheses being ruled out == gaining evidence for a hypothesis. In what sense have we not gained any information on the viability of approach X? We've learned that one of the alternatives to X (the at least 13 OOM alternative) won't happen.
We do gain evidence on at least some alternatives, but not on all the factors which determine the alternatives. If we know something about those factors, we can't usually just renormalise. That's a good default, but it amounts to an assumption of ignorance.
Here's a simple example:
We play a 'game' where you observe the outcome of two fair coin tosses x and y.
You score:
1 if x is heads
2 if x is tails and y is heads
3 if x is tails and y is tails
So your score predictions start out at:
1 : 50%
2 : 25%
3 : 25%
We look at y and see that it's heads. This rules out 3.
Renormalising would get us:
1 : 66.7%
2 : 33.3%
3: 0%
This is clearly silly, since we ought to end up at 50:50 - i.e. all the mass from 3 should go to 2. This happens because the evidence that falsified 3 points was insignificant to the question "did you score 1 point?".
On the other hand, if we knew nothing about the existence of x or y, and only knew that we were starting from (1: 50%, 2: 25%, 3: 25%), and that 3 had been ruled out, it'd make sense to re-normalise.
In the TAI case, we haven't only learned that 12 OOM is probably enough (if we agree on that). Rather we've seen specific evidence that leads us to think 12 OOM is probably enough. The specifics of that evidence can lead us to think things like "This doesn't say anything about TAI at +4 OOM, since my prediction for +4 is based on orthogonal variables", or perhaps "This makes me near-certain that TAI will happen by +10 OOM, since the +12 OOM argument didn't require more than that".
Interesting, hmm.
In the 1-2-3 coin case, seeing that y is heads rules out 3, but it also rules out half of 1. (There are two 1 hypotheses, the yheads and the ytails version) To put it another way, terms P(yheads|1)=0.5. So we are ruling-out-and-renormalizing after all, even though it may not appear that way at first glance.
The question is, is something similar happening with the AI OOMs?
I think if the evidence leads us to think things like "This doesn't say anything about TAI at +4 OOM, since my prediction is based on orthogonal variables" then that's a point in my favor, right? Or is the idea that the hypotheses ruled out by the evidence presented in the post include all the >12OOM hypotheses, but also a decent chunk of the <6OOM hypotheses but not of the 7-12 OOM hypotheses such that overall the ratio of (our credence in 7-12 OOMs)/(our credence in 0 - 6 OOMs) increases?
"This makes me near-certain that TAI will happen by +10 OOM, since the +12 OOM argument didn't require more than that" also seems like a point in my favor. FWIW I also had the sense that the +12OOM argument didn't really require 12 OOMs, it would have worked almost as well with 10.
Yes, we're always renormalising at the end - it amounts to saying "...and the new evidence will impact all remaining hypotheses evenly". That's fine once it's true.
I think perhaps I wasn't clear with what I mean by saying "This doesn't say anything...".
I meant that it may say nothing in absolute terms - i.e. that I may put the same probability of [TAI at 4 OOM] after seeing the evidence as before.
This means that it does say something relative to other not-ruled-out hypotheses: if I'm saying the new evidence rules out >12 OOM, and I'm also saying that this evidence should leave p([TAI at 4 OOM]) fixed, I'm implicitly claiming that the >12 OOM mass must all go somewhere other than the 4 OOM case.
Again, this can be thought of as my claiming e.g.:
[TAI at 4 OOM] will happen if and only if zwomples work
There's a 20% chance zwomples work
The new 12 OOM evidence says nothing at all about zwomples
In terms of what I actually think, my sense is that the 12 OOM arguments are most significant where [there are no high-impact synergistic/amplifying/combinatorial effects I haven't thought of].
My credence for [TAI at < 4 OOM] is largely based on such effects. Perhaps it's 80% based on some such effect having transformative impact, and 20% on we-just-do-straightforward-stuff. [Caveat: this is all just ottomh; I have NOT thought for long about this, nor looked at much evidence; I think my reasoning is sound, but specific numbers may be way off]
Since the 12 OOM arguments are of the form we-just-do-straightforward-stuff, they cause me to update the 20% component, not the 80%. So the bulk of any mass transferred from >12 OOM, goes to cases where p([we-just-did-straightforward-stuff and no strange high-impact synergies occurred]|[TAI first occurred at this level]) is high.
I think I'm just not seeing why you think the >12 OOM mass must all go somewhere than the <4 OOM (or really, I would argue, <7 OOM) case. Can you explain more?
Maybe the idea is something like: There are two underlying variables, 'We'll soon get more ideas' and 'current methods scale.' If we get new ideas soon, then <7 are needed. If we don't but 'current methods scale' is true, 7-12 are needed. If neither variable is true then >12 is needed. So then we read my +12 OOMs post and become convinced that 'current methods scale.' That rules out the >12 hypothesis, but the renormalized mass doesn't go to <7 at all because it also rules out a similar-sized chunk of the <7 hypothesis (the chunk that involved 'current methods don't scale'). This has the same structure as your 1, 2, 3 example above.
Is this roughly your view? If so, nice, that makes a fair amount of sense to me. I guess I just don't think that the "current methods scale" hypothesis is confined to 7-12 OOMs; I think it is a probability distribution that spans many OOMs starting with mere +1, and my post can be seen as an attempt to upper-bound how high the distribution goes--which then has implications for how low it goes also, if you want to avoid the anti-spikiness objection. Another angle: I could have made a similar post for +9 OOMs, and a similar one for +6 OOMs, and each would have been somewhat less plausible than the previous. But (IMO) not that much less plausible; if you have 80% credence in +12 then I feel like you should have at least 50% by +9 and at least, idk, 25% by +6. If your credence drops faster than that, you seem overconfident in your ability to extrapolate from current data IMO (or maybe not, I'd certainly love to hear your arguments!)
[[ETA, I'm not claiming the >12 OOM mass must all go somewhere other than the <4 OOM case: this was a hypothetical example for the sake of simplicity. I was saying that if I had such a model (with zwomples or the like), then a perfectly good update could leave me with the same posterior credence on <4 OOM.
In fact my credence on <4 OOM was increased, but only very slightly]]
First I should clarify that the only point I'm really confident on here is the "In general, you can't just throw out the >12 OOM and re-normalise, without further assumptions" argument.
I'm making a weak claim: we're not in a position of complete ignorance w.r.t. the new evidence's impact on alternate hypotheses.
My confidence in any specific approach is much weaker: I know little relevant data.
That said, I think the main adjustment I'd make to your description is to add the possibility for sublinear scaling of compute requirements with current techniques. E.g. if beyond some threshold meta-learning efficiency benefits are linear in compute, and non-meta-learned capabilities would otherwise scale linearly, then capabilities could scale with the square root of compute (feel free to replace with a less silly example of your own).
This doesn't require "We'll soon get more ideas" - just a version of "current methods scale" with unlucky (from the safety perspective) synergies.
So while the "current methods scale" hypothesis isn't confined to 7-12 OOMs, the distribution does depend on how things scale: a higher proportion of the 1-6 region is composed of "current methods scale (very) sublinearly".
My p(>12 OOM | sublinear scaling) was already low, so my p(1-6 OOM | sublinear scaling) doesn't get much of a post-update boost (not much mass to re-assign).
My p(>12 OOM | (super)linear scaling) was higher, but my p(1-6 OOM | (super)linear scaling) was low, so there's not too much of a boost there either (small proportion of mass assigned).
I do think it makes sense to end up with a post-update credence that's somewhat higher than before for the 1-6 range - just not proportionately higher. I'm confident the right answer for the lower range lies somewhere between [just renormalise] and [don't adjust at all], but I'm not at all sure where.
Perhaps there really is a strong argument that the post-update picture should look almost exactly like immediate renormalisation. My main point is that this does require an argument: I don't think its a situation where we can claim complete ignorance over impact to other hypotheses (and so renormalise by default), and I don't think there's a good positive argument for [all hypotheses will be impacted evenly].
OK, thanks.
1. I concede that we're not in a position of complete ignorance w.r.t. the new evidence's impact on alternate hypotheses. However, the same goes for pretty much any argument anyone could make about anything. In my particular case I think there's some sense in which, plausibly, for most underlying views on timelines people will have, my post should cause an update more or less along the lines I described. (see below)
2. Even if I'm wrong about that, I can roll out the anti-spikiness argument to argue in favor of <7 OOMs, though to be fair I don't make this argument in the post. (The argument goes: If 60%+ of your probability mass is between 7 and 12 OOMs, you are being overconfident.)
Argument that for most underlying views on timelines people will have, my post should cause an update more or less along the lines I described:
--The only way for your credence in <7 to go down relative to your credence in7-12 after reading my post and (mostly) ruling out >12 hypotheses, is for the stuff you learn to also disproportionately rule out sub-hypotheses in the <7 range compared to sub-hypotheses in the 7-12 range. But this is a bit weird; my post didn't talk about the <7 range at all, so why would it disproportionately rule out stuff in that range? Like I said, it seems like (to a first approximation) the information content of my post was "12 OOMs is probably enough" and not something more fancy like "12 OOMs is probably enough BUT 6 is probably not enough." I feel unsure about this and would like to hear you describe the information content of the post, in your terms.
--I actually gave an argument that this should increase your relative credence in <7 compared to 7-12, and it's a good one I think: The arguments that 12 OOMs are probably enough are pretty obviously almost as strong for 11 OOMs, and almost as strong as that for 10 OOMs, and so on. To put it another way, our distribution shouldn't have a sharp cliff at 12 OOMs; it should start descending several OOMs prior. What this means is that actually stuff in the 7-12 OOM range is disproportionately ruled out compared to stuff in the <7 OOM range, so we should actually be more confident in <7 OOMs than you would be if you just threw out >12 OOM and renormalized.
Taking your last point first: I entirely agree on that. Most of my other points were based on the implicit assumption that readers of your post don't think something like "It's directly clear that 9 OOM will almost certainly be enough, by a similar argument".
Certainly if they do conclude anything like that, then it's going to massively drop their odds on 9-12 too. However, I'd still make an argument of a similar form: for some people, I expect that argument may well increase the 5-8 range more (than proportionately) than the 1-4 range.
On (1), I agree that the same goes for pretty-much any argument: that's why it's important. If you update without factoring in (some approximation of) your best judgement of the evidence's impact on all hypotheses, you're going to get the wrong answer. This will depend highly on your underlying model.
On the information content of the post, I'd say it's something like "12 OOMs is probably enough (without things needing to scale surprisingly well)". My credence for low OOM values is mostly based on worlds where things scale surprisingly well.
But this is a bit weird; my post didn't talk about the <7 range at all, so why would it disproportionately rule out stuff in that range?
I don't think this is weird. What matters isn't what the post talks about directly - it's the impact of the evidence provided on the various hypotheses. There's nothing inherently weird about evidence increasing our credence in [TAI by +10OOM] and leaving our credence in [TAI by +3OOM] almost unaltered (quite plausibly because it's not too relevant to the +3OOM case).
Compare the 1-2-3 coins example: learning y tells you nothing about the value of x. It's only ruling out any part of the 1 outcome in the sense that it maintains [x_heads & something independent is heads], and rules out [x_heads & something independent is tails]. It doesn't need to talk about x to do this.
You can do the same thing with the TAI first at k OOM case - call that Tk. Let's say that your post is our evidence e and that e+ stands for [e gives a compelling argument against T13+].
Updating on e+ you get the following for each k:
Initial hypotheses: [Tk & e+], [Tk & e-]
Final hypothesis: [Tk & e+]
So what ends up mattering is the ratio p[Tk | e+] : p[Tk | e-]
I'm claiming that this ratio is likely to vary with k.
Specifically, I'd expect T1 to be almost precisely independent of e+, while I'd expect T8 to be correlated. My reason on the T1 is that I think something radically unexpected would need to occur for T1 to hold, and your post just doesn't seem to give any evidence for/against that.
I expect most people would change their T8 credence on seeing the post and accepting its arguments (if they've not thought similar things before). The direction would depend on whether they thought the post's arguments could apply equally well to ~8 OOM as 12.
Note that I am assuming the argument ruling out 13+ OOM is as in the post (or similar).
If it could take any form, then it could be a more or less direct argument for T1.
Overall, I'd expect most people who agree with the post's argument to update along the following lines (but smoothly):
T0 to Ta: low increase in credence
Ta to Tb: higher increase in credence
Tb+: reduced credence
with something like (0 < a < 6) and (4 < b < 13).
I'm pretty sure a is going to be non-zero for many people.
So what ends up mattering is the ratio p[Tk | e+] : p[Tk | e-]
I'm claiming that this ratio is likely to vary with k.
Wait, shouldn't it be the ratio p[Tk & e+] : p[Tk & e-]? Maybe both ratios work fine for our purposes, but I certainly find it more natural to think in terms of &.
Unless I've confused myself badly (always possible!), I think either's fine here. The | version just takes out a factor that'll be common to all hypotheses: [p(e+) / p(e-)]. (since p(Tk & e+) ≡ p(Tk | e+) * p(e+))
Since we'll renormalise, common factors don't matter. Using the | version felt right to me at the time, but whatever allows clearer thinking is the way forward.
I'm probably being just mathematically confused myself; at any rate, I'll proceed with the p[Tk & e+] : p[Tk & e-] version since that comes more naturally to me. (I think of it like: Your credence in Tk is split between two buckets, the Tk&e+ and Tk&e- bucket, and then when you update you rule out the e- bucket. So what matters is the ratio between the buckets; if it's relatively high (compared to the ratio for other Tx's) your credence in Tk goes up, if it's relatively low it goes down.
Anyhow, I totally agree that this ratio matters and that it varies with k. In particular here's how I think it should vary for most readers of my post:
for k>12, the ratio should be low, like 0.1.
for low k, the ratio should be higher.
for middling k, say 6<k<13, the ratio should be in between.
Thus, the update should actually shift probability mass disproportionately to the lower k hypotheses.
I realize we are sort of arguing in circles now. I feel like we are making progress though. Also, separately, want to hop on a call with me sometime to sort this out? I've got some more arguments to show you...
Summary of why I think the post's estimates are too low as estimates of what's required for a system capable of seizing a decisive strategic advantage:
To be an APS-like system OmegaStar needs to be able to control robots or model real world stuff and also plan over billions, not hundreds of action steps.
Each of those problems adds on a few extra OOMs that aren't accounted for in e.g. the setup for Omegastar (which can transfer learn across tens of thousands of games, each requiring thousands of action steps to win in a much less complicated environment than the real world).
You'd need something that can transfer learn across tens of thousands of 'games' each requiring billions of action steps, each one of which has way more sensory input to parse than StarCraft per time step.
When you correct Omegastar's requirements by adding on (1) a factor for number of action steps needed to win a war Vs win a game of StarCraft, (2) a factor for the real world Vs StarCraft's complexity of sensory input and. When you do this, the total requirement would look more like Ajeya's reports.
I still get the intuition that OmegaStar would not just be a fancy game player! I find it hard to think about what it would be like - maybe good at gaming quite constrained systems or manipulating people?
Therefore, I think the arguments provide a strong case (unless scaling laws break - which I also think is fairly likely for technical reasons) for 'something crazy happening by 2030' but less strong a case for 'AI takeover by 2030'
Summary of mine and Daniel's disagreements:
(1) Horizon Length: Daniel thinks we'll get a long way towards planning over a billion action steps 'for free' if we transfer learn over lots of games that take a thousand action steps each - so the first correction factor I gave is a lot smaller than it seems just by comparing the raw complexity of StarCraft Vs fighting a war
(2) No Robots: the complexity in sensory input difference doesn't matter since the system won't need to control robots [Or, as I should have also said, build robot-level models of the external world even if you're not running the actuators yourself] - so the second correction factor isn't an issue, because-
(3) Lower capability threshold: to take a DSA doesn't require as many action steps as it seems or as many capabilities as often assumed. You can just do it by taking to people and over a smaller number of action steps than it would take to conquer the world yourself.
To me, it seems like Daniel's view on horizon length reducing one of the upward corrections (1) is doing less total work than (2) and (3) in terms of shortening the timeline - hence this view looks to me like a case of plausible DSA from narrow AI with specialized abilities. Although point taken that it won't look that narrow to most people today.
(Re scaling laws - there's a whole debate I about how scaling laws are just a v crude observable for what's really going on, so we shouldn't be confident in extrapolation. This is also all conditional on the underlying assumptions of these forecasting models being correct.)
I tentatively endorse this summary. Thanks! And double thanks for the links on scaling laws.
I'm imagining doom via APS-AI that can't necessarily control robots or do much in the physical world, but can still be very persuasive to most humans and accumulate power in the normal ways (by convincing people to do what you want, the same way every politician, activist, cult leader, CEO, general, and warlord does it). If this is classified as narrow AI, then sure, that's a case of narrow AI takeover.
Man, I haven't had time to thoroughly review this, but given that it's an in-depth review of another post up for review, it seems sad not to include it.