This is awesome, thanks! I found the minesweeper analogy in particular super helpful.
4. Combining (4) and (5), PU(PS)≥2−(KU(ϕ)+O(1))PU(NPS). QED.
Typo? Maybe you mean (2 and (3)?
More substantively, on the simplicity prior stuff:
There's the power seeking functions and the non-power-seeking functions, but then there's also the inner-aligned functions, i.e. the ones that are in some sense trying their best to achieve the base objective, and then there's also the human-aligned functions. Perhaps we can pretty straightforwardly argue that the non-power-seeking functions have much higher prior than those other two categories?
Sketch:
The simplest function period is probably at least 20 bits simpler than the simplest inner-aligned function and the simplest human-aligned function. Therefore (given previous theorems) the simplest power-seeking function is at least 5 bits simpler than the simplest inner-aligned function and the simplest human-aligned function, and therefore probably the power-seeking functions are significantly more likely on priors than the inner-aligned and human-aligned functions.
Seems pretty plausible to me, no? Of course the constant isn't really 15 bits, but... isn't it plausible that the constant is smaller than the distance between the simplest possible function and the simplest inner-aligned one? At least for the messy, complex training environments that we realistically expect for these sorts of things? And obviously for human-aligned functions the case is even more straightforward...
I like the thought. I don't know if this sketch works out, partly because I don't fully understand it. your conclusion seems plausible but I want to develop the arguments further.
As a note: the simplest function period probably is the constant function, and other very simple functions probably make both power-seeking and not-power-seeking optimal. So if you permute that one, you'll get another function for which power-seeking and not-power-seeking actions are both optimal.
Oh interesting... so then what I need for my argument is not the simplest function period, but the simplest function that doesn't make both power-seeking and not-power-seeking both optimal? (isn't that probably just going to be the simplest function that doesn't make everything optimal?)
I admit I am probably conceptually confused in a bunch of ways, I haven't read your post closely yet.
Another typo:
I don't yet understand the general case, but I have a strong hunch that instrumental convergenceoptimal policies is a governed by how many more ways there are for power to be optimal than not optimal.
Planned summary for the Alignment Newsletter:
We have <@previously seen@>(@Seeking Power is Provably Instrumentally Convergent in MDPs@) that if you are given an optimal policy for some reward function, but are very uncertain about that reward function (specifically, your belief assigns reward to states in an iid manner), you should expect that the optimal policy will navigate towards states with higher power in some but not all situations. This post generalizes this to non-iid reward distributions: specifically, that "at least half" of reward distributions will seek power (in particular circumstances).
The new results depend on the notion of _environment symmetries_, which arise in states in which an action a2 leads to “more options” than another action a1 (we’re going to ignore cases where a1 or a2 is a self-loop). Specifically, a1 leads to a part of the state space that is isomorphic to a subgraph of the part of the state space that a2 leads to. For example, a1 might be going to a store where you can buy books or video games, and a2 might be going to a supermarket where you can buy food, plants, cleaning supplies, tools, etc. Then, one subgraph isomorphism would be the one that maps “local store” to “supermarket”, “books” to “food”, and “video games” to “plants”. Another such isomorphism would instead map “video games” to “tools”, while keeping the rest the same.
Now this alone doesn’t mean that an optimal policy is definitely going to take a2. Maybe you really want to buy books, so a1 is the optimal choice! But for every reward function for which a1 is optimal, we can construct another reward function for which a2 is optimal, by mapping it through the isomorphism. So, if your first reward function highly valued books, this would now construct a new reward function that highly values food, and now a1 will be optimal. Thus, at least half of the possible reward functions (or distributions over reward functions) will prefer a2 over a1. Thus, in cases where these isomorphisms exist, optimal policies will tend to seek more options (which in turn means they are seeking power).
If the agent is sufficiently farsighted (i.e. the discount is near 1), then we can extend this analysis out in time, to the final cycle that an agent ends up in. (It must end up in a cycle because by assumption the state space is finite.) Any given cycle would only count as one “option”, and so ending up in any given cycle is not very likely (using a similar argument of constructing other rewards). If shutdown is modeled as a state with a single self-loop and no other actions, then this implies that optimal policies will tend to avoid entering the shutdown state.
We’ve been saying “we can construct this other reward function under which the power-seeking action is optimal”. An important caveat is that maybe we know that this other reward function is very unlikely. For example, maybe we really do just know that we’re going to like books and not care much about food, and so the argument “well, we can map the book-loving reward to a food-loving reward” isn’t that interesting, because we assign high probability to the first and low probability to the second. We can’t rule this out for what humans actually do in practice, but it isn’t as simple as “a simplicity prior would do the right thing” -- for any non-power-seeking reward function, we can create a power-seeking reward function with only slightly higher complexity by having a program that searches for a subgraph isomorphism and then applies it to the non-power-seeking reward function to create a power-seeking version.
Another major caveat is that this all relies on the existence of these isomorphisms / symmetries in the environment. It is still a matter of debate whether good models of the environment will exhibit such isomorphisms.
If the agent is sufficiently farsighted (i.e. the discount is near 1)
I'd change this to "optimizes average reward (i.e. the discount equals 1)". Otherwise looks good!
(we’re going to ignore cases where a1 or a2 is a self-loop)
I think that a more general class of things should be ignored here. For example, if a2 is part of a 2-cycle, we get the same problem as when a2 is a self-loop. Namely, we can get that most reward functions have optimal policies that take the action a1 over a2 (when the discount rate is sufficiently close to 1), which contradicts the claim being made.
Thanks for the correction.
That one in particular isn't a counterexample as stated, because you can't construct a subgraph isomorphism for it. When writing this I thought that actually meant I didn't need more of a caveat (contrary to what I said to you earlier), but now thinking about it a third time I really do need the "no cycles" caveat. The counterexample is:
Z <--> S --> A --> B
With every state also having a self-loop.
In this case, the involution {S:B, Z:A}, would suggest that S --> Z would have more options than S --> A, but optimal policies will take S --> A more often than S --> Z.
(The theorem effectively says "no cycles" by conditioning on the policy being S --> Z or S --> A, in which case the S --> Z --> S --> S --> ... possibility is not actually possible, and the involution doesn't actually go through.)
EDIT: I've changed to say that the actions lead to disjoint parts of the state space.
My take on it has been, the theorem's bottleneck assumption implies that you can't reach S again after taking action a1 or a2, which rules out cycles.
That one in particular isn't a counterexample as stated, because you can't construct a subgraph isomorphism for it.
Probably not an important point, but I don't see why we can't use the identity isomorphism (over the part of the state space that a1 leads to).
This particular argument is not talking about farsightedness -- when we talk about having more options, each option is talking about the entire journey and exact timesteps, rather than just the destination. Since all the "journeys" starting with the S --> Z action go to Z first, and all the "journeys" starting with the S --> A action go to A first, the isomorphism has to map A to Z and vice versa, so that .
(What assumption does this correspond to in the theorem? In the theorem, the involution has to map to a subset of ; every possibility in starts with A, and every possibility in starts with Z, so you need to map A to Z.)
I don't understand what you mean. Nothing contradicts the claim, if the claim is made properly, because the claim is a theorem and always holds when its preconditions do. (EDIT: I think you meant Rohin's claim in the summary?)
I'd say that we can just remove the quoted portion and just explain "a1 and a2 lead to disjoint sets of future options", which automatically rules out the self-loop case. (But maybe this is what you meant, ofer?)
I was referring to the claim being made in Rohin's summary. (I no longer see counter examples after adding the assumption that "a1 and a2 lead to disjoint sets of future options".)
The original version of this post claimed that an MDP-independent constant C helped lower-bound the probability assigned to power-seeking reward functions under simplicity priors. This constant is not actually MDP-independent (at least, the arguments given don't show that): the proof sketch assumes that the MDP is given as input to the permutation-finding algorithm (which is the same, for every MDP you want to apply it to!). But the input's description length must also be part of the Kolmogorov complexity (else you could just compute any string for free by saying "the identity program outputs the string, given the string as input").
The upshot is that the given lower bound is weaker for more complex environments. There are other possible recourses, like "at least half of the permutations of any NPS element will be PS element, and they surely can't all be high-complexity permutations!" — but I leave that open for now.
Oops, and fixed.
Added to the post:
Relatedly [to power-seeking under the simplicity prior], Rohin Shah wrote:
if you know that an agent is maximizing the expectation of an explicitly represented utility function, I would expect that to lead to goal-driven behavior most of the time, since the utility function must be relatively simple if it is explicitly represented, and simple utility functions seem particularly likely to lead to goal-directed behavior.
I've ended up spending probably more than 40 hours discussing, thinking and reading this paper (including earlier versions; the paper was first published on December 2019, and the current version is the 7th, published on June 1st, 2021). My impression is very different than Adam Shimi's. The paper introduces many complicated definitions that build on each other, and its theorems say complicated things using those complicated definitions. I don't think the paper explains how its complicated theorems are useful/meaningful.
In particular, I don't think the paper provides a simple description for the set of MDPs that the main claim in the abstract applies to ("We prove that for most prior beliefs one might have about the agent's reward function […], one should expect optimal policies to seek power in these environments."). Nor do I think that the paper justifies the relevance of that set of MDPs. (Why is it useful to prove things about it?)
I think this paper should probably not be used for outreach interventions (even if it gets accepted to NeurIPS/ICML). And especially, I think it should not be cited as a paper that formally proves a core AI alignment argument.
Also, there may be a misconception that this paper formalizes the instrumental convergence thesis. That seems wrong, i.e. the paper does not seem to claim that several convergent instrumental values can be identified. The only convergent instrumental value that the paper attempts to address AFAICT is self-preservation (avoiding terminal states).
(The second version of the paper said: "Theorem 49 answers yes, optimal farsighted agents will usually acquire resources". But the current version just says "Extrapolating from our results, we conjecture that Blackwell optimal policies tend to seek power by accumulating resources[…]").
Sorry for the awkwardness (this comment was difficult to write). But I think it is important that people in the AI alignment community publish these sorts of thoughts. Obviously, I can be wrong about all of this.
For my part, I either strongly disagree with nearly every claim you make in this comment, or think you're criticizing the post for claiming something that it doesn't claim (e.g. "proves a core AI alignment argument"; did you read this post's "A note of caution" section / the limitations section and conclusion of the paper?).
I don't think it will be useful for me to engage in detail, given that we've already extensively debated these points at length, without much consensus being reached.
For my part, I either strongly disagree with nearly every claim you make in this comment, or think you're criticizing the post for claiming something that it doesn't claim (e.g. "proves a core AI alignment argument"; did you read this post's "A note of caution" section / the limitations section and conclusion of the paper v.7?).
I did read the "Note of caution" section in the OP. It says that most of the environments we think about seem to "have the right symmetries", which may be true, but I haven't seen the paper support that claim.
Maybe I just missed it, but I didn't find a "limitations section" or similar in the paper. I did find the following in the Conclusion section:
We caution that many real-world tasks are partially observable and that learned policies are rarely optimal. Our results do not mathematically prove that hypothetical superintelligent AI agents will seek power.
Though the title of the paper can still give the impression that it proves a core argument for AI x-risk.
Also, plausibly-the-most-influential-critic-of-AI-safety in EA seems to have gotten the impression (from an earlier version of the paper) that it formalizes the instrumental convergence thesis (see the first paragraph here). So I think my advice that "it should not be cited as a paper that formally proves a core AI alignment argument" is beneficial.
I don't think it will be useful for me to engage in detail, given that we've already extensively debated these points at length, without much consensus being reached.
For reference (in case anyone is interested in that discussion): I think it's the thread that starts here (just the part after "2.").
I haven't seen the paper support that claim.
The paper supports the claim with:
- Embodied environment in a vase-containing room (section 6.3)
- Pac-Man (figure 8)
- And section 7 argues why this generally holds whenever the agent can be shut down (a large class of environments indeed)
- Average-optimal robots not idling in a particular spot (beginning of section 7)
This post supports the claim with:
- Tic-Tac-Toe
- Vase gridworld
- SafeLife
So yes, this is sufficient support for speculation that most relevant environments have these symmetries.
Maybe I just missed it, but I didn't find a "limitations section" or similar in the paper.
Sorry - I meant the "future work" portion of the discussion section 7. The future work highlights the "note of caution" bits. I also made sure that the intro emphasizes that the results don't apply to learned policies.
Also, plausibly-the-most-influential-critic-of-AI-safety in EA seems to have gotten the impression (from an earlier version of the paper) that it formalizes the instrumental convergence thesis (see the first paragraph here).
Key part: earlier version of the paper. (I've talked to Ben since then, including about the newest results, their limitations, and their usefulness.)
I think my advice that "it should not be cited as a paper that formally proves a core AI alignment argument" is beneficial.
Your advice was beneficial a year ago, because that was a very different paper. I think it is no longer beneficial: I still agree with it, but I don't think it needs to be mentioned on the margin. At this point, I have put far more care into hedging claims than most other work which I can recall. At some point, you're hedging too much. And I'm not interested in hedging any more, unless I've made some specific blatant oversights which you'd like to inform me of.
The paper supports the claim with:
- Embodied environment in a vase-containing room (section 6.3)
I think this refers to the following passage from the paper:
Consider an embodied navigation task through a room with a vase. Proposition 6.9 suggests that optimal policies tend to avoid breaking the vase, since doing so would strictly decrease available options.
This seems to me like a counter example. For any reward function that does not care about breaking the vase, the optimal policies do not avoid breaking the vase.
Regarding your next bullet point:
- Pac-Man (figure 8)
- And section 7 argues why this generally holds whenever the agent can be shut down (a large class of environments indeed)
I don't know what you mean here by "generally holds". When does an environment—in which the agent can be shut down—"have the right symmetries" for the purpose of the main claim? Consider the following counter example (in which the last state is equivalent to the agent being shut down):
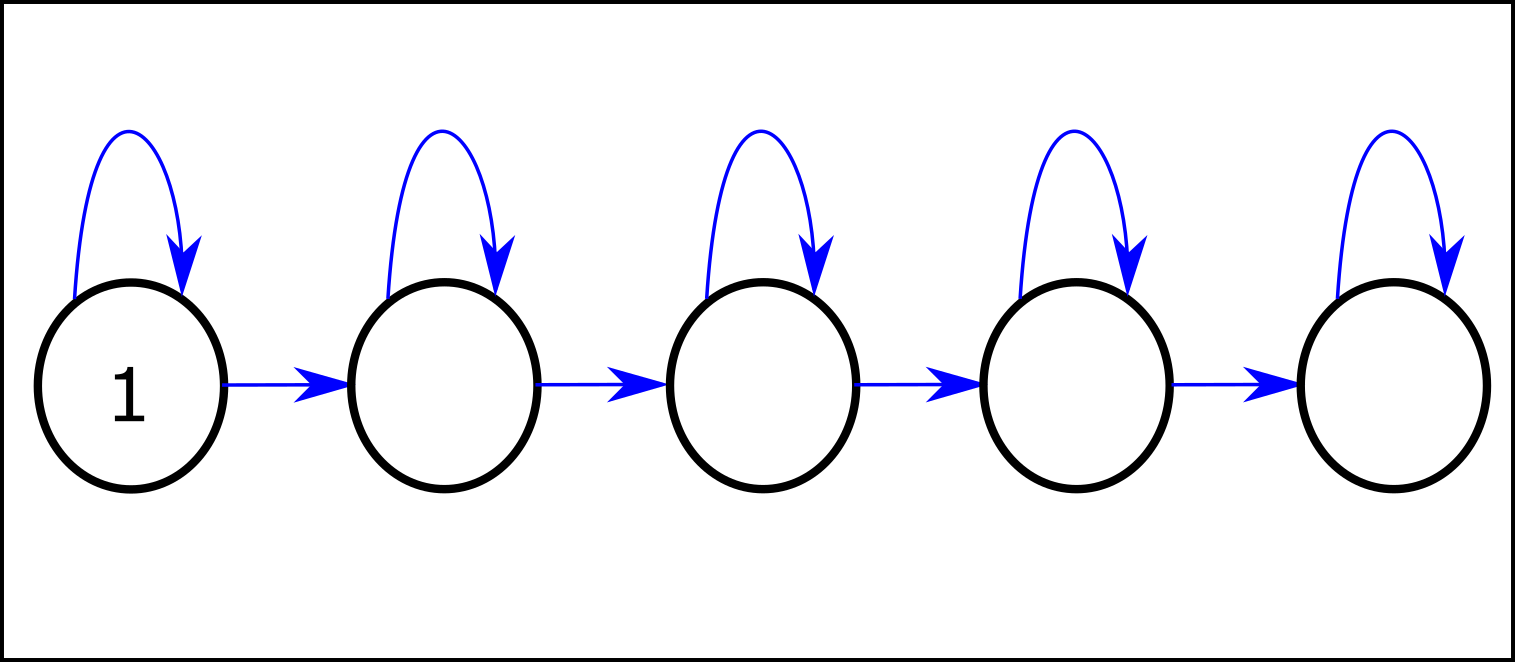
In most states (the first 3 states) the optimal policies of most reward functions transition to the next state, while the POWER-seeking behavior is to stay in the same state (when the discount rate is sufficiently close to 1). If we want to tell a story about this environment, we can say that it's about a car in a one-way street.
To be clear, the issue I'm raising here about the paper is NOT that the main claim does not apply to all MDPs. The issue is the lack of (1) a reasonably simple description of the set of MDPs that the main claim applies to; and (2) an explanation for why it is useful to prove things about that set.
Sorry - I meant the "future work" portion of the discussion section 7. The future work highlights the "note of caution" bits.
The limitations mentioned there are mainly: "Most real-world tasks are partially observable" and "our results only apply to optimal policies in finite MDPs". I think that another limitation that belongs there is that the main claim only applies to a particular set of MDPs.
This seems to me like a counter example. For any reward function that does not care about breaking the vase, the optimal policies do not avoid breaking the vase.
There are fewer ways for vase-breaking to be optimal. Optimal policies will tend to avoid breaking the vase, even though some don't.
Consider the following counter example (in which the last state is equivalent to the agent being shut down):
This is just making my point - average-optimal policies tend to end up in any state but the last state, even though at any given state they tend to progress. If is {the first four cycles} and is {the last cycle}, then average-optimal policies tend to end up in instead of . Most average-optimal policies will avoid entering the final state, just as section 7 claims. (EDIT: Blackwell -> average-)
(And I claim that the whole reason you're able to reason about this environment is because my theorems apply to them - you're implicitly using my formalisms and frames to reason about this environment, while seemingly trying to argue that my theorems don't let us reason about this environment? Or something? I'm not sure, so take this impression with a grain of salt.)
Why is it interesting to prove things about this set of MDPs? At this point, it feels like someone asking me "why did you buy a hammer - that seemed like a waste of money?". Maybe before I try out the hammer, I could have long debates about whether it was a good purchase. But now I know the tool is useful because I regularly use it and it works well for me, and other people have tried it and say it works well for them.
I agree that there's room for cleaner explanation of when the theorems apply, for those readers who don't want to memorize the formal conditions. But I think the theory says interesting things because it's already starting to explain the things I built it to explain (e.g. SafeLife). And whenever I imagine some new environment I want to reason about, I'm almost always able to reason about it using my theorems (modulo already flagged issues like partial observability etc). From this, I infer that the set of MDPs is "interesting enough."
Optimal policies will tend to avoid breaking the vase, even though some don't.
Are you saying that the optimal policies of most reward functions will tend to avoid breaking the vase? Why?
This is just making my point - Blackwell optimal policies tend to end up in any state but the last state, even though at any given state they tend to progress. If D1 is {the first four cycles} and D2 is {the last cycle}, then optimal policies tend to end up in D1 instead of D2. Most optimal policies will avoid entering the final state, just as section 7 claims.
My question is just about the main claim in the abstract of the paper ("We prove that for most prior beliefs one might have about the agent's reward function [...], one should expect optimal policies to seek power in these environments."). The main claim does not apply to the simple environment in my example (i.e. we should not expect optimal policies to seek POWER in that environment). I'm completely fine with that being the case, I just want to understand why. What criterion does that environment violate?
I agree that there's room for cleaner explanation of when the theorems apply, for those readers who don't want to memorize the formal conditions.
I counted ~19 non-trivial definitions in the paper. Also, the theorems that the main claim directly relies on (which I guess is some subset of {Proposition 6.9, Proposition 6.12, Theorem 6.13}?) seem complicated. So I think the paper should definitely provide a reasonably simple description of the set of MDPs that the main claim applies to, and explain why proving things on that set is useful.
But I think the theory says interesting things because it's already starting to explain the things I built it to explain (e.g. SafeLife). And whenever I imagine some new environment I want to reason about, I'm almost always able to reason about it using my theorems (modulo already flagged issues like partial observability etc). From this, I infer that the set of MDPs is "interesting enough."
Do you mean that the main claim of the paper actually applies to those environments (i.e. that they are in the formal set of MDPs that the relevant theorems apply to) or do you just mean that optimal policies in those environments tend to be POWER-seeking? (The main claim only deals with sufficient conditions.)
Are you saying that the optimal policies of most reward functions will tend to avoid breaking the vase? Why?
Because you can do "strictly more things" with the vase (including later breaking it) than you can do after you break it, in the sense of proposition 6.9 / lemma D.49. This means that you can permute breaking-vase-is-optimal objectives into breaking-vase-is-suboptimal objectives.
What criterion does that environment violate?
Right, good question. I'll explain the general principle (not stated in the paper - yes, I agree this needs to be fixed!), and then answer your question about your environment. When the agent maximizes average reward, we know that optimal policies tend to seek power when there's something like:
"Consider state s, and consider two actions a1 and a2. When {cycles reachable after taking a1 at s} is similar to a subset of {cycles reachable after taking a2 at s}, and those two cycle sets are disjoint, then a2 tends to be optimal over a1 and a2 tends to seek power compared to a1." (This follows by combining proposition 6.12 and theorem 6.13)
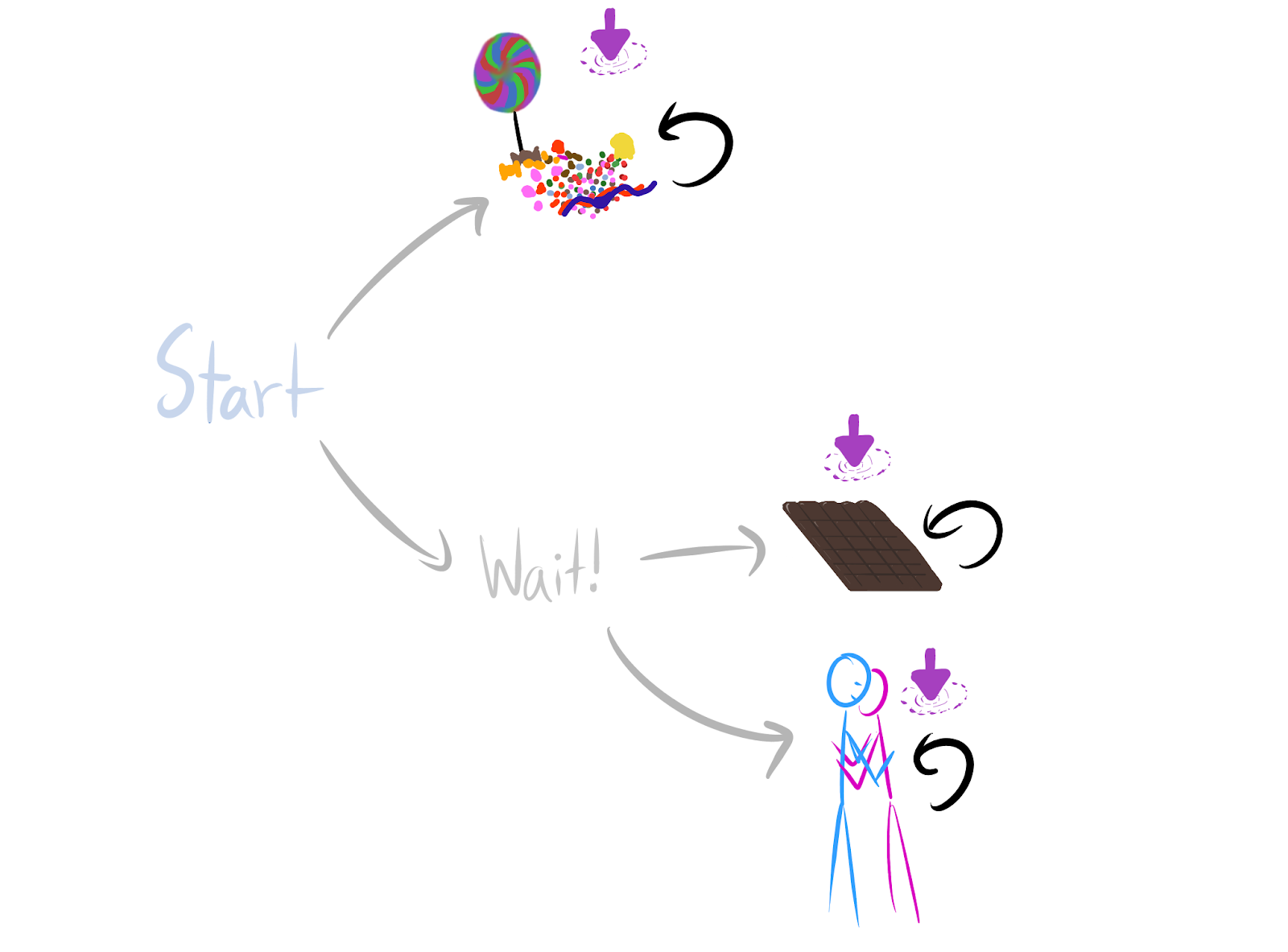
start, let a1 go to candy and let a2 go to wait. This satisfies the criterion: Wait! tends to be optimal and it tends to have more POWER, as expected.Let's reconsider your example:

Again, I very much agree that this part needs more explanation. Currently, the main paper has this to say:

Throughout the paper, I focused on the survival case because it automatically satisfies the above criterion (death is definitionally disjoint from non-death, since we assume you can't do other things while dead), without my having to use limited page space explaining the nuances of this criterion.
Do you mean that the main claim of the paper actually applies to those environments
Yes, although SafeLife requires a bit of squinting (as I noted in the main post). Usually I'm thinking about RSDs in those environments.
Because you can do "strictly more things" with the vase (including later breaking it) than you can do after you break it, in the sense of proposition 6.9 / lemma D.49. This means that you can permute breaking-vase-is-optimal objectives into breaking-vase-is-suboptimal objectives.
Most of the reward functions are either indifferent about the vase or want to break the vase. The optimal policies of all those reward functions don't "tend to avoid breaking the vase". Those optimal policies don't behave as if they care about the 'strictly more states' that can be reached by not breaking the vase.
When the agent maximizes average reward, we know that optimal policies tend to seek power when there's something like:
"Consider state s, and consider two actions a1 and a2. When {cycles reachable after taking a1 at s} is similar to a subset of {cycles reachable after taking a2 at s}, and those two cycle sets are disjoint, then a2 tends to be optimal over a1 and a2 tends to seek power compared to a1." (This follows by combining proposition 6.12 and theorem 6.13)
Here "{cycles reachable after taking a1 at s}" actually refers an RSD, right? So we're not just talking about a set of states, we're talking about a set of vectors that each corresponds to a "state visitation distribution" of a different policy. In order for the "similar to" (via involution) relation to be satisfied, we need all the elements (real numbers) of the relevant vector pairs to match. This is a substantially more complicated condition than the one in your comment, and it is generally harder to satisfy in stochastic environments.
In fact, I think that condition is usually hard/impossible to satisfy even in toy stochastic environments. Consider a version of Pac-Man in which at least one "ghost" is moving randomly at any given time; I'll call this Pac-Man-with-Random-Ghost (a quick internet search suggests that in the real Pac-Man the ghosts move deterministically other than when they are in "Frightened" mode, i.e. when they are blue and can't kill Pac-Man).
Let's focus on the condition in Proposition 6.12 (which is identical to or less strict than the condition for the main claim, right?). Given some state in a Pac-Man-with-Random-Ghost environment, suppose that action a1 results in an immediate game-over state due to a collision with a ghost, while action a2 does not. For every terminal state , is a set that contains a single vector in which all entries are 0 except for one that is non-zero. But for every state that can result from action a2, we get that is a set that does not contain any vector-with-0s-in-all-entries-except-one, because for any policy, there is no way to get to a particular terminal state with probability 1 (due to the location of the ghosts being part of the state description). Therefore there does not exist a subset of that is similar to via an involution.
A similar argument seems to apply to Propositions 6.5 and 6.9. Also, I think Corollary 6.14 never applies to Pac-Man-with-Random-Ghost environments, because unless s is a terminal state, will not contain any vector-with-0s-in-all-entries-except-one (again, due to ghosts moving randomly). The paper claims (in the context of Figure 8 which is about Pac-Man): "Therefore, corollary 6.14 proves that Blackwell optimal policies tend to not go left in this situation. Blackwell optimal policies tend to avoid immediately dying in PacMan, even though most reward functions do not resemble Pac-Man’s original score function." So that claim relies on Pac-Man being a "sufficiently deterministic" environment and it does not apply to the Pac-Man-with-Random-Ghost version.
Can you give an example of a stochastic environment (with randomness in every state transition) to which the main claim of the paper applies?
Most of the reward functions are either indifferent about the vase or want to break the vase. The optimal policies of all those reward functions don't "tend to avoid breaking the vase". Those optimal policies don't behave as if they care about the 'strictly more states' that can be reached by not breaking the vase.
This is factually wrong BTW. I had just explained why the opposite is true.
Are you saying that my first sentence ("Most of the reward functions are either indifferent about the vase or want to break the vase") is in itself factually wrong, or rather the rest of the quoted text?
Thanks.
We can construct an involution over reward functions that transforms every state by switching the is-the-vase-broken bit in the state's representation. For every reward function that "wants to preserve the vase" we can apply on it the involution and get a reward function that "wants to break the vase".
(And there are the reward functions that are indifferent about the vase which the involution map to themselves.)
Gotcha. I see where you're coming from.
I think I underspecified the scenario and claim. The claim wasn't supposed to be: most agents never break the vase (although this is sometimes true). The claim should be: most agents will not immediately break the vase.
If the agent has a choice between one action ("break vase and move forwards") or another action ("don't break vase and more forwards"), and these actions lead to similar subgraphs, then at all discount rates, optimal policies will tend to not break the vase immediately. But they might tend to break it eventually, depending on the granularity and balance of final states.
So I think we're actually both making a correct point, but you're making an argument for under certain kinds of models and whether the agent will eventually break the vase. I (meant to) discuss the immediate break-it-or-not decision in terms of option preservation at all discount rates.
[Edited to reflect the ancestor comments]
The claim should be: most agents will not immediately break the vase.
I don't see why that claim is correct either, for a similar reason. If you're assuming here that most reward functions incentivize avoiding immediately breaking the vase then I would argue that that assumption is incorrect, and to support this I would point to the same involution from my previous comment.
I‘m not assuming that they incentivize anything. They just do! Here’s the proof sketch (for the full proof, you’d subtract a constant vector from each set, but not relevant for the intuition).
&You’re playing a tad fast and loose with your involution argument. Unlike the average-optimal case, you can’t just map one set of states to another for all-discount-rates reasoning.
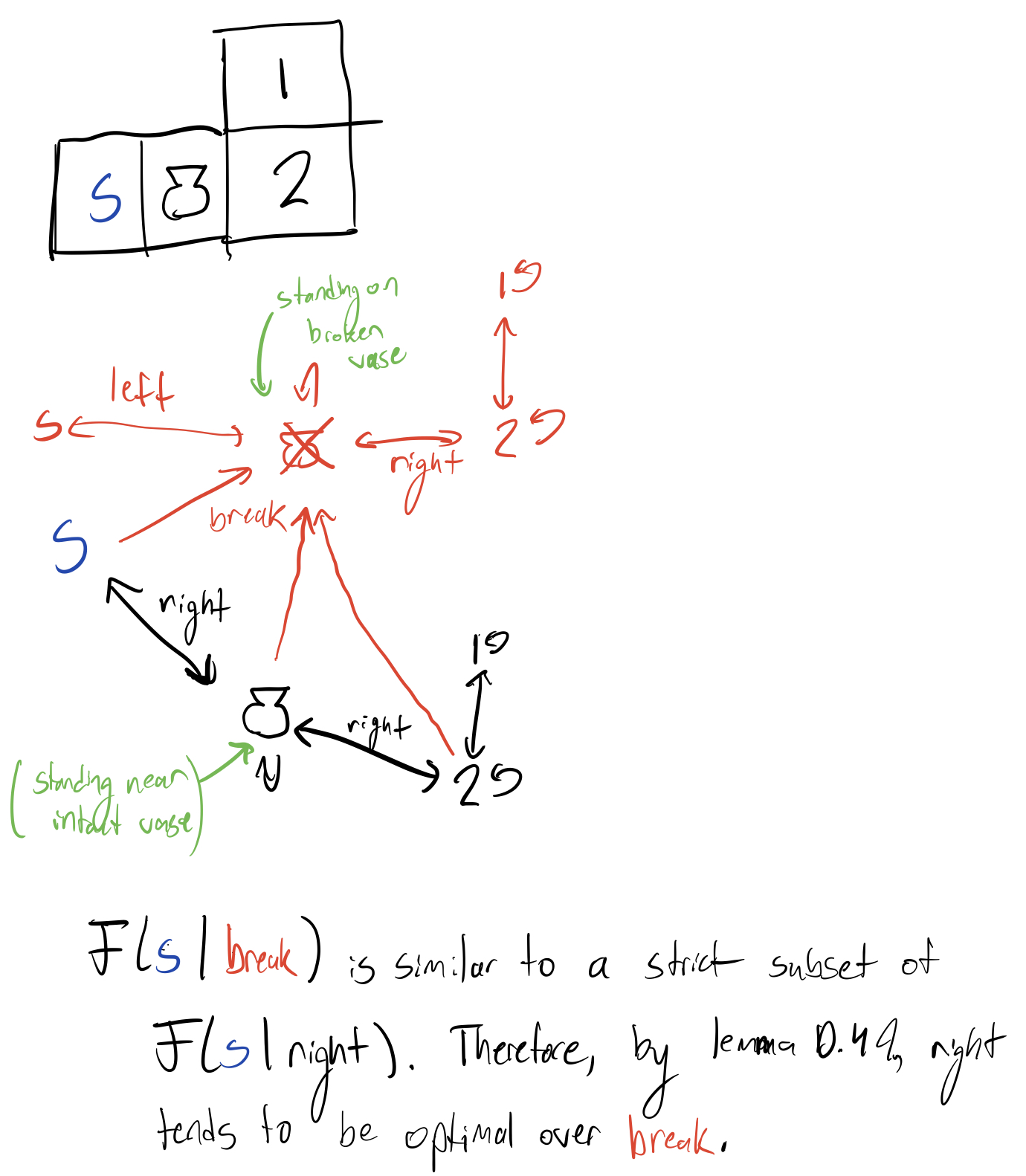
Thanks for the figure. I'm afraid I didn't understand it. (I assume this is a gridworld environment; what does "standing near intact vase" mean? Can the robot stand in the same cell as the intact vase?)
&You’re playing a tad fast and loose with your involution argument. Unlike the average-optimal case, you can’t just map one set of states to another for all-discount-rates reasoning.
I don't follow (To be clear, I was not trying to apply any theorem from the paper via that involution). But does this mean you are NOT making that claim ("most agents will not immediately break the vase") in the limit of the discount rate going to 1? My understanding is that the main claim in the abstract of the paper is meant to assume that setting, based on the following sentence from the paper:
Proposition 6.5 and proposition 6.9 are powerful because they apply to all , but they can only be applied given hard-to-satisfy environmental symmetries.
Sorry for the awkwardness (this comment was difficult to write). But I think it is important that people in the AI alignment community publish these sorts of thoughts. Obviously, I can be wrong about all of this.
Despite disagreeing with you, I'm glad that you published this comment and I agree that airing up disagreements is really important for the research community.
In particular, I don't think the paper provides a simple description for the set of MDPs that the main claim in the abstract applies to ("We prove that for most prior beliefs one might have about the agent's reward function […], one should expect optimal policies to seek power in these environments."). Nor do I think that the paper justifies the relevance of that set of MDPs. (Why is it useful to prove things about it?)
There's a sense in which I agree with you: AFAIK, there is no formal statement of the set of MDPs with the structural properties that Alex studies here. That doesn't mean it isn't relatively easy to state:
- Proposition 6.9 requires that there is a state with two actions and such that (let's say) leads to a subMDP that can be injected/strictly injected into the subMDP that leads to.
- Theorems 6.12 and 6.13 require that there is a state with two actions and such that (let's say) leads to a set of RSDs (final cycles that are strictly optimal for some reward function) that can be injected/strictly injected into the set of RSDs from .
The first set of MDPs is quite restrictive (because you need an exact injection), which is why IIRC Alex extends the results to the sets of RSDs, which captures a far larger class of MDPs. Intuitively, this is the class of MDPs such that some action leads to more infinite horizon behaviors than another for the same state. I personally find this class quite intuitive, and also I feel like it captures many real world situations where we worry about power and instrumental convergence.
Also, there may be a misconception that this paper formalizes the instrumental convergence thesis. That seems wrong, i.e. the paper does not seem to claim that several convergent instrumental values can be identified. The only convergent instrumental value that the paper attempts to address AFAICT is self-preservation (avoiding terminal states).
Once again, I agree in part with the statement that the paper doesn't IIRC explicitly discuss different convergent instrumental goals. On the other hand, the paper explicitly says that it focus on a special case of the instrumental convergence thesis.
An action is instrumental to an objective when it helps achieve that objective. Some actions are instrumental to many objectives, making them robustly instrumental. The claim that power-seeking is robustly instrumental is a specific instance of the instrumental convergence thesis:
Several instrumental values can be identified which are convergent in the sense that their attainment would increase the chances of the agent’s goal being realized for a wide range of final goals and a wide range of situations, implying that these instrumental values are likely to be pursued by a broad spectrum of situated intelligent agents [Bostrom, 2014].
That being said, you just made me want to look more into how well power-seeking captures different convergent instrumental goals from Omohundro's paper, so thanks for that. :)
Meta: it seems that my original comment was silently removed from the AI Alignment Forum. I ask whoever did this to explain their reasoning here. Since every member of the AF could have done this AFAIK, I'm going to try to move my comment back to AF, because I think it obviously belongs there (I don't believe we have any norms about this sort of situations...). If the removal was done by a forum moderator/admin, please let me know.
My apologies - I had thought I had accidentally moved your comment to AF by unintentionally replying to your comment on AF, and so (from my POV) I "undid" it (for both mine and yours). I hadn't realized it was already on AF.
No worries, thanks for the clarification.
[EDIT: the confusion may have resulted from me mentioning the LW username "adamShimi", which I'll now change to the display name on the AF ("Adam Shimi").]
Edit, 5/16/23: I think this post is beautiful, correct in its narrow technical claims, and practically irrelevant to alignment. This post presents a cripplingly unrealistic picture of the role of reward functions in reinforcement learning. Reward functions are not "goals", real-world policies are not "optimal", and the mechanistic function of reward is (usually) to provide policy gradients to update the policy network.
I expect this post to harm your alignment research intuitions unless you've already inoculated yourself by deeply internalizing and understanding Reward is not the optimization target. If you're going to read one alignment post I've written, read that one.
Follow-up work (Parametrically retargetable decision-makers tend to seek power) moved away from optimal policies and treated reward functions more realistically.
Previously: Seeking Power Is Often Robustly Instrumental In MDPs
Key takeaways.
More generally, the new results say something like: in a range of situations, for most beliefs you could have about the agent's objective, these beliefs assign high probability to reward functions for which power-seeking is optimal.
Thanks to TheMajor, Rafe Kennedy, and John Wentworth for feedback on this post. Thanks for Rohin Shah and Adam Shimi for feedback on the simplicity prior result.
Orbits Contain All Permutations of an Objective Function
The Minesweeper analogy for power-seeking risks
One view on AGI risk is that we're charging ahead into the unknown, into a particularly unfair game of Minesweeper in which the first click is allowed to blow us up. Following the analogy, we want to understand enough about the mine placement so that we don't get exploded on the first click. And once we get a foothold, we start gaining information about other mines, and the situation is a bit less dangerous.
My previous theorems on power-seeking said something like: "at least half of the tiles conceal mines."
I think that's important to know. But there are many tiles you might click on first. Maybe all of the mines are on the right, and we understand the obvious pitfalls, and so we'll just click on the left.
That is: we might not uniformly randomly select tiles:
There are lots of ways to sample coordinates, besides uniformly randomly. So why should our sampling procedure tend to activate mines?
My new results say something analogous to: for every coordinate, either it contains a mine, or its reflection across x=y contains a mine, or both. Therefore, for every distribution D over tile coordinates, either D assigns at least 12 probability to mines, or it does after you reflect it across x=y.
Definition. The orbit of a coordinate C under the symmetric group S2 is {C,Creflected}. More generally, if we have a probability distribution over coordinates, its orbit is the set of all possible "permuted" distributions.
Orbits under symmetric groups quantify all ways of "changing things around" for that object.
But it didn't have to be this way.
Since my results (in the analogy) prove that at least one of the two blue coordinates conceals a mine, we deduce that the mines are not all on the right.
Some reasons we care about orbits:
In terms of coordinates, one hope could have been:
But suppose you give me a program P which computes a safe coordinate. Let P′ call P to compute the coordinate, and then have P′ swap the entries of the computed coordinate. P′ is only a few bits longer than P, and it doesn't take much longer to compute, either. So the above hope is impossible: safe mine-selection procedures can't be significantly simpler or faster than unsafe mine-selection procedures.
(The section "Simplicity priors assign non-negligible probability to power-seeking" proves something similar about objective functions.)
Orbits of goals
Orbits of goals consist of all the ways of permuting what states get which values. Consider this rewardless Markov decision process (MDP):
Whenever staying put at A is strictly optimal, you can permute the reward function so that it's strictly optimal to go to B. For example, let R(A):=1,R(B):=0 and let ϕ:=(AB) swap the two states. ϕ acts on R as follows: ϕ⋅R simply permutes the state before evaluating its reward: (ϕ⋅R)(s):=R(ϕ(s)).
The orbit of R is {R,ϕ⋅R}. It's optimal for the former to stay at A, and for the latter to alternate between the two states.
Here, let RC assign 1 reward to C and 0 to all other states, and let ϕ:=(ABC) rotate through the states (A goes to B, B goes to C, C goes to A). Then the orbit of RC is:
My new theorems prove that in many situations, for every reward function, power-seeking is incentivized by most (at least half) of its orbit elements.
In All Orbits, Most Elements Incentivize Power-Seeking
In Seeking Power is Often Robustly Instrumental in MDPs, the last example involved gems and dragons and (most exciting of all) subgraph isomorphisms:
The state permutation ϕ embeds the red-gem-subgraph into the blue-gem-subgraph:
We say that ϕ is an environmental symmetry, because ϕ is an element of the symmetric group S|S| of permutations on the state space.
The key insight was right there the whole time
Let's pause for a moment. For half a year, I intermittently and fruitlessly searched for some way of extending the original results beyond IID reward distributions to account for arbitrary reward function distributions.
The recurring thought which kept my hope alive was:
Imagine how I felt when I realized that the same state permutation ϕ which proved my original IID-reward theorems - the one that says
- that same permutation ϕ holds the key to understanding instrumental convergence in MDPs.
red-gemsis optimal. For example, let R🏰 assign 1 reward to the castle 🏰 , and 0 to all other states. Then the permuted reward function ϕ⋅R🏰 assigns 1 reward to the gold pile, and 0 to all other states, and soblue-gemshas strictly more optimal value thanred-gems.Consider any discount rate γ∈(0,1). For all reward functions R such that V∗R(red-gems,γ)>V∗R(blue-gems,γ), this permutation ϕ turns them into
blue-gemlovers: V∗ϕ⋅R(red-gems,γ)<V∗ϕ⋅R(blue-gems,γ).ϕ takes non-power-seeking reward functions, and injectively maps them to power-seeking orbit elements. Therefore, for all reward functions R, at least half of the orbit of R must agree that
blue-gemsis optimal!Throughout this post, when I say "most" reward functions incentivize something, I mean the following:
Definition. At state s, most reward functions incentivize action a over action a′ when for all reward functions R, at least half of the orbit agrees that a has at least as much action value as a′ does at state s. (This is actually a bit weaker than what I prove in the paper, but it's easier to explain in words; see definition 6.4 for the real deal.)
The same reasoning applies to distributions over reward functions. And so if you say "we'll draw reward functions from a simplicity prior", then most permuted distributions in that prior's orbit will incentivize power-seeking in the situations covered by my previous theorems. (And we'll later prove that simplicity priors themselves must assign non-trivial, positive probability to power-seeking reward functions.)
Furthermore, for any distribution which distributes reward "fairly" across states (precisely: independently and identically), their (trivial) orbits unanimously agree that
blue-gemshas strictly greater probability of being optimal. And so the converse isn't true: it isn't true that at least half of every orbit agrees thatred-gemshas more POWER and greater probability of being optimal.This might feel too abstract, so let's run through examples.
And this directly generalizes the previous theorems
More graphical options (proposition 6.9)
blue-gemsbecause that leads to strictly more options. We can permute everyred-gemsreward function into ablue-gemsreward function.destroying-vase-is-optimalcan be permuted into apreserving-vase-is-optimalreward function", my results (specifically, proposition 6.9 and its generalization via lemma D.49) suggest that optimal policies tend to avoid breaking the vase, since doing so would strictly decrease available options.("Suggest" instead of "prove" because D.49's preconditions may not always be met, depending on the details of the dynamics. I think this is probably unimportant, but that's for future work. EDIT: Also, the argument may barely not apply to this gridworld, but if you could move the vase around without destroying it, I think it goes through fine.)
destroy-green-patternreward function can be permuted into apreserve-green-patternreward function", lemma D.49 suggests that optimal policies tend to not disturb any given green cell pattern (although most probably destroy some pattern). The permutation would swap {states reachable after destroying the pattern} with {states reachable after not destroying the pattern}.However, the converse is not true: you cannot fix a permutation which turns all
preserve-green-patternreward functions intodestroy-green-patternreward functions. There are simply too many extra ways for preserving green cells to be optimal.Assuming some conjectures I have about the combinatorial properties of power-seeking, this helps explain why AUP works in SafeLife using a single auxiliary reward function - but more on that in another post.
Terminal options (theorem 6.13)
Wait!so that they can choose betweenchocolateandhug. The logic is that everycandy-optimalreward function can be permuted into achocolate-optimalreward function.lose-immediately-with-given-black-movereward function can be permuted into astay-alive-with-green-movereward function.Even though randomly generated environments are unlikely to satisfy these sufficient conditions for power-seeking tendencies, the results are easy to apply to many structured environments common in reinforcement learning. For example, when γ≈1, most reward functions provably incentivize not immediately dying in Pac-Man. Every reward function which incentivizes dying right away can be permuted into a reward function for which survival is optimal.
Most importantly, we can prove that when shutdown is possible, optimal policies try to avoid it if possible. When the agent isn't discounting future reward (i.e. maximizes average return) and for lots of reasonable state/action encodings, the MDP structure has the right symmetries to ensure that it's instrumentally convergent to avoid shutdown. From the discussion section:
Takeaways
Combinatorics, how do they work?
What does 'most reward functions' mean quantitatively - is it just at least half of each orbit? Or, are there situations where we can guarantee that at least three-quarters of each orbit incentivizes power-seeking? I think we should be able to prove that as the environment gets more complex, there are combinatorially more permutations which enforce these similarities, and so the orbits should skew harder and harder towards power-incentivization.
candystrictly optimal when γ=1, ϕchocolate and ϕhug respectively produce Rϕchocolate≠Rϕhug.Wait!is strictly optimal for both Rϕhug,Rϕhug, and so at least 23 of the orbit should agree thatWait!is optimal. AsWait!gains more power (more choices, more control over the future), I conjecture that this fraction approaches 1.I don't yet understand the general case, but I have a strong hunch that instrumental convergenceoptimal policies is governed by how many more ways there are for power to be optimal than not optimal. And this seems like a function of the number of environmental symmetries which enforce the appropriate embedding.
Simplicity priors assign non-negligible probability to power-seeking
Note: this section is more technical. You can get the gist by reading the English through "Theorem..." and then after the end of the "FAQ."
One possible hope would have been:
Unfortunately, there are always power-seeking reward functions not much more complex than their non-power-seeking counterparts. Here, 'power-seeking' corresponds to the intuitive notions of either keeping strictly more options open (proposition 6.9), or navigating towards larger sets of terminal states (theorem 6.13). (Since this applies to several results, I'll leave the meaning a bit ambiguous, with the understanding that it could be formalized if necessary.)
Theorem (Simplicity priors assign non-negligible probability to power-seeking). Consider any MDP which meets the preconditions of proposition 6.9 or theorem 6.13. Let U be a universal Turing machine, and let PU be the U-simplicity prior over computable reward functions.
Let NPS be the set of non-power-seeking computable reward functions which choose a fixed non-power-seeking action in the given situation. Let PS be the set of computable reward functions for which seeking power is strictly optimal.1
Then there exists a "reasonably small" constant C such that PU(PS)≥2−CPU(NPS), where C .
Proof sketch.
Since PU is a simplicity prior, PU(ϕ(NPS))≥2−(KU(ϕ)+O(1))PU(NPS).
FAQ.
Even if that equation held, that would mean that power-seeking is (at least weakly) optimal for all computable reward functions. That's hardly a reassuring situation.
Takeaways from the simplicity prior result
EDIT: Relatedly, Rohin Shah wrote:
Why optimal-goal-directed alignment may be hard by default
For every reward function R - no matter how benign, how aligned with human interests, no matter how power-averse - either R or its permuted variant ϕ⋅R seeks power in the given situation (intuitive-power, since the agent keeps its options open, and also formal-POWER, according to my proofs).
If I let myself be a bit more colorful, every reward function has lots of "evil" power-seeking variants (do note that the step from "power-seeking" to "misaligned power-seeking" requires more work). If we imagine ourselves as only knowing the orbit of the agent's objective, then the situation looks a bit like this:
Of course, this isn't how reward specification works - we probably are far more likely to specify certain orbit elements than others. However, the formal theory is now beginning to explain why alignment is so hard by default, and why failure might be catastrophic!
The structure of the environment often ensures that there are (potentially combinatorially) many more ways to misspecify the objective so that it seeks power, than there are ways to specify goals without power-seeking incentives.
Other convergent phenomena
I'm optimistic that symmetry arguments and the mental models gained by understanding these theorems, will help us better understand a range of different tendencies. The common thread seems like: for every "way" a thing could not happen / not be a good idea - there are many more "ways" in which it could happen / be a good idea.
Note of caution
You have to be careful in applying these results to argue for real-world AI risk from deployed systems.
This list of limitations has steadily been getting shorter over time. If you're interested in making it even shorter, message me.
Conclusion
I think that this work is beginning to formally explain why slightly misspecified reward functions will probably incentivize misaligned power-seeking. Here's one hope I have for this line of research going forwards:
One super-naive alignment approach involves specifying a good-seeming reward function, and then having an AI maximize its expected discounted return over time. For simplicity, we could imagine that the AI can just instantly compute an optimal policy.
Let's precisely understand why this approach seems to be so hard to align, and why extinction seems to be the cost of failure. We don't yet know how to design beneficial AI, but we largely agree that this naive approach is broken. Let's prove it.
1 There are reward functions for which it's optimal to seek power and not to seek power; for example, constant reward functions make everything optimal, and they're certainly computable. Therefore, NPS∪PS is a strict subset of the whole set of computable reward functions.