

This is a fascinating result, but there is a caveat worth noting. When we say that e.g. AlphaGo is "superhuman at go" we are comparing it humans who (i) spent years training on the task and (ii) were selected for being the best at it among a sizable population. On the other hand, with next token prediction we're nowhere near that amount of optimization on the human side. (That said, I also agree that optimizing a model on next token prediction is very different from optimizing it for text coherence would be, if we could accomplish the latter.)
Yeah, I agree that it would be kind of interesting to see how good humans would get at this if it was a competitive sport. I still think my guess is that the best humans would be worse than GPT-3, and I'm unsure if they're worse than GPT-2.
(There's no limit on anyone spending a bunch of time practicing this game, if for some reason someone gets really into it I'd enjoy hearing about the results.)
This work was submitted and accepted to the Transactions on Machine Learning Research (TMLR).
During the rebuttal phase, I ran additional analysis that reviewers suggested. I found that:
A big reason why humans suck at NTP in our experiments is that they suck at tokenization:
A potential reason why humans have terrible perplexity is that they aren't good at having fine-grained probability when doing comparison of likelihood between tokens:
The updated paper can be found on arxiv: https://arxiv.org/pdf/2212.11281
Overall, I think the original results reported in the paper were slightly overstated. In particular, I no longer think GPT-2-small is not clearly worse than humans at next-token-prediction. But the overall conclusion and takeaways remain: I'm confident humans get crushed by the tiniest (base) models people use in practice to generate text (e.g. StableLM-1.6B).
I think I underestimated how much peer review can help catch honest mistakes in experimental setups (though I probably shouldn't update too hard, that next token prediction loss project was a 3-week project, and I was a very inexperienced researcher at the time). Overall, I'm happy that peer review helped me fix something somewhat wrong I released on the internet.
This post's point still seems correct, and it still seems important--I refer to it at least once a week.
The limitations detailed above are probably why these results are not consistent with estimation of human perplexity by Shannon, who estimated the average per-character perplexity to be between 0.6 and 1.3 bits, which would result in a per-token perplexity between 7 and 60 (the average length of tokens in our corpus is 4.5).
Shannon's estimate was about a different quantity. Shannon was interested in bounding character-level entropy of an ideal predictor, ie. what we'd consider a perfect language model, though he leveraged human performance on the predict-the-next-character task to make his estimate.
This article cites a paper saying that, when human-level perplexity was measured on the same dataset that Shannon used, a higher estimate was obtained that is consistent with your estimate.
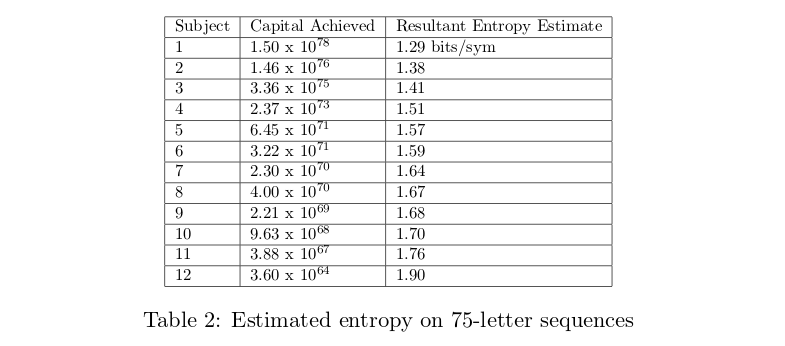
Cover and King framed prediction as a gambling problem. They let the subject “wager a percentage of his current capital in proportion to the conditional probability of the next symbol." If the subject divides his capital on each bet according to the true probability distribution of the next symbol, then the true entropy of the English language can be inferred from the capital of the subject after n wagers.
Separately, in my opinion, a far better measure of human-level performance at language modeling is the perplexity level at which a human judge can no longer reliably distinguish between a long sequence of generated text and a real sequence of natural language. This measure has advantage that, if well-measured human-level ability is surpassed, we can directly substitute language models for human writers.
Thanks for the response! We've rewritten the paragraph starting "The limitations detailed..." for clarity.
Some brief responses to your points:
Shannon's estimate was about a different quantity. [...]
We agree that Shannon was interested in something else - the "true" entropy of English, using an ideal predictor for English. However, as his estimates of entropy used his wife Mary Shannon and Barnard Oliver as substitutes for his ideal predictor, we think it's still fair to treat this as an estimate of the entropy/perplexity of humans on English text.
This article cites a paper saying that [...]
As you point out, there's definitely been a bunch of follow up work which find various estimates of the entropy/perplexity of human predictors. The Cover and King source you find above does give a higher estimate consistent with our results. Note their estimator shares many of the same pitfalls of our estimator - for example, if subjects aren't calibrated, they'll do quite poorly with respect to both the Cover and King estimator and our estimator. We don't really make any claims that our results are surprising relative to all other results in this area, merely noting that our estimate is inconsistent with perhaps the most widely known one.
Separately, in my opinion, a far better measure of human-level performance at language modeling is the perplexity level at which a human judge can no longer reliably distinguish between a long sequence of generated text and a real sequence of natural language.
The measure you suggest is similar the methodology used by Shen et al 2017 to get a human level perplexity estimate of 12, which we did mention and criticize in our writeup.
We disagree that this measure is better. Our goal here isn't to compare the quality of Language Models to the quality of human-generated text; we aimed to compare LMs and humans on the metric that LMs were trained on (minimize log loss/perplexity when predicting the next token). As our work shows, Language Models whose output has significantly worse quality than human text (such as GPT-2 small) can still significantly outperform humans on next token prediction. We think it's interesting that this happens, and speculated a bit more on the takeaways in the conclusion.
We disagree that this measure is better. Our goal here isn't to compare the quality of Language Models to the quality of human-generated text; we aimed to compare LMs and humans on the metric that LMs were trained on (minimize log loss/perplexity when predicting the next token).
Your measure is great for your stated goal. That said, I feel the measure gives a misleading impression to readers. In particular I'll point to this paragraph in the conclusion,
Even current large language models are wildly superhuman at language modeling. This is important to remember when you’re doing language model interpretability, because it means that you should expect your model to have a lot of knowledge about text that you don’t have. Chris Olah draws a picture where he talks about the possibility that models become more interpretable as they get to human level, and then become less interpretable again as they become superhuman; the fact that existing LMs are already superhuman (at the task they’re trained on) is worth bearing in mind when considering this graph.
I think it's misleading to say that language models are "wildly superhuman at language modeling" by any common-sense interpretation of that claim. While the claim is technically true if one simply means that languages do better at the predict-the-next-token task, most people (I'd imagine) would not intuitively imagine that to be the best measure of general performance at language modeling. The reason, fundamentally, is that we are building language models to compete with other humans at the task of writing text, not the task of predicting the next character.
By analogy, if we train a robot to play tennis by training it to emulate human tennis players, I think most people would think that "human level performance" is reached when it can play as well as a human, not when it can predict the next muscle movement of an expert player better than humans, even if predicting the next muscle movement was the task used during training.
Ah, I see your point. That being said, I think calling the task we train our LMs to do (learn a probabilistic model of language) "language modeling" seems quite reasonable to me - in my opinion, it seems far more unreasonable to call "generating high quality output" "language modeling". For one thing, there are many LM applications that aren't just "generate high quality text"! There's a whole class of LMs like BERT that can't really be used for text generation at all.
One reason we at Redwood care about this result is that we want to interpret modern LMs. As outlined in the linked Chris Olah argument, we might intuitively expect that AIs get more interpretable as they get to human level performance, then less interpretable as their performance becomes more and more superhuman. If LMs were ~human level at the task they are trained on, we might hope that they contain mainly crisp abstractions that humans find useful for next token prediction. However, since even small LMs are superhuman at next token prediction, they probably contain alien abstractions that humans can't easily understand, which might pose a serious problem for interpretability efforts.
Ah, I see your point. That being said, I think calling the task we train our LMs to do (learn a probabilistic model of language) "language modeling" seems quite reasonable to me - in my opinion, it seems far more unreasonable to call "generating high quality output" "language modeling".
Note that the main difference between my suggested task and the next-character-prediction task is that I'm suggesting we measure performance over a long time horizon. "Language models" are, formally, probability distributions over sequences of text, not models over next characters within sequences. It is only via a convenient application of the Markov assumption and the chain rule of probability that we use next-character-prediction during training.
The actual task, in the sense of what language models are fundamentally designed to perform well on, is to emulate sequences of human text. Thus, it is quite natural to ask when they can perform well on this task. In fact, I remain convinced that it is more natural to ask about performance on the long-sequence task than the next-character-prediction task.
In fact, I remain convinced that it is more natural to ask about performance on the long-sequence task than the next-character-prediction task.
Large language models are also going to be wildly superhuman by long-sequence metrics like "log probability assigned to sequences of Internet text" (in particular because many such metrics are just sums over the next-character versions of the metric, which this post shows LLMs are great at).
LLMs may not be superhuman at other long-sequence tasks like "writing novels" but those seem like very different tasks, just like "playing already-composed music" and "composing new music" are very different tasks for humans.
(To be clear, I think it's fair to say that what we care about with LLMs is the latter category of stuff, but let's not call that "language modeling".)
Large language models are also going to be wildly superhuman by long-sequence metrics like "log probability assigned to sequences of Internet text"
I think this entirely depends on what you mean. There's a version of the claim here that I think is true, but I think the most important version of it is actually false, and I'll explain why.
I claim that if you ask a human expert to write an article (even a relatively short one) about a non-trivial topic, their output will have a higher log probability than a SOTA language model, with respect to the "true" distribution of internet articles. That is, if you were given the (entirely hypothetical) true distribution of actual internet articles (including articles that have yet to be written, and the ones that have been written in other parts of the multiverse...), a human expert is probably going to write an article that has a higher log probability of being sampled from this distribution, compared to a SOTA language model.
This claim might sound bizarre at first, because, as you noted "many such metrics are just sums over the next-character versions of the metric, which this post shows LLMs are great at". But, first maybe think about this claim from first principles: what is the "true" distribution of internet articles? Well, it's the distribution of actual internet articles that humans write. If a human writes an article, it's got to have pretty high log-probability, no? Because otherwise, what are we even sampling from?
Now, what you could mean is that instead of measuring the log probability of an article with respect to the true distribution of internet articles, we measure it with respect to the empirical distribution of internet articles. This is in fact what we use to measure the log-probability of next character predictions. But the log probability of this quantity over long sequences will actually be exactly negative infinity, both for the human-written article, and for the model-written article, assuming they're not just plagiarizing an already-existing article. That is, we aren't going to find any article in the empirical distribution that matches the articles either the human or the model wrote, so we can't tell which of the two is better from this information alone.
What you probably mean is that we could build a model of the true distribution of internet articles, and use this model to estimate the log-probability of internet articles. In that case, I agree, a SOTA language model would probably far outperform the human expert, at the task of writing internet articles, as measured by the log-probability given by another model. But, this is a flawed approach, because the model we're using to estimate the log-probability with respect to the true distribution of internet articles is likely to be biased in favor of the SOTA model, precisely because it doesn't understand things like long-sequence coherence, unlike the human.
How could we modify this approach to give a better estimate of the performance of a language model at long-sequence prediction? I think that there's a relatively simple approach that could work.
Namely, we set up a game in which humans try to distinguish between real human texts and generated articles. If the humans can't reliably distinguish between the two, then the language model being used to generate the articles has attained human-level performance (at least by this measure). This task has nice properties, as there is a simple mathematical connection between prediction ability and ability to discriminate; a good language model that can pass this test will likely only pass it because it is good at coming up with high log-probability articles. And this task also measures the thing we care about that’s missing from the predict-the-next-character task: coherence over long sequences.
But, first maybe think about this claim from first principles: what is the "true" distribution of internet articles? Well, it's the distribution of actual internet articles that humans write. If a human writes an article, it's got to have pretty high log-probability, no? Because otherwise, what are we even sampling from?
I continue to think you are making a point about generation / sampling, whereas language modeling is about modeling the distribution as a whole.
Put another way, even if I am better than the LLM at the specific part of the Internet text distribution that is "articles written by Rohin", that does not mean that I am better than the LLM at modeling the entire distribution of Internet text (long horizon or not).
Even under your proposed game, I don't think I can get to indistinguishability, if the discriminator is allowed to learn over time (which seems like the version that properly tests language modeling). They'll notice peculiarities of my writing style and aspects of Internet writing style that I'm not able to mimic very well. If your proposed test was "when can LLMs beat humans at this game" that seems more reasonable (though it still advantages the humans because the judge is a human; similarly I expect that if the judge was an LLM that would advantage the LLMs relative to the humans).
What you probably mean is that we could build a model of the true distribution of internet articles, and use this model to estimate the log-probability of internet articles.
I don't think this point depends on thinking about having a model of the true distribution of articles that we use to evaluate humans vs LLMs; I'm happy to talk about the true distribution directly (to the extent that a "true distribution" exists). (This gets tricky though because you could say that in the true distribution coherence errors ~never happen and so LLM outputs have zero probability, but this is basically dooming the LLM to never be superhuman by defining the true distribution to be "what humans output", which seems like a symptom of a bad definition.)
Let me restate some of my points, which can hopefully make my position clearer. Maybe state which part you disagree with:
Language models are probability distributions over finite sequences of text.
The “true distribution” of internet text refers to a probability distribution over sequences of text that you would find on the internet (including sequences found on other internets elsewhere in the multiverse, which is just meant as an abstraction).
A language model is “better” than another language model to the extent that the cross-entropy between the true distribution and the model is lower.
A human who writes a sequence of text is likely to write something with a relatively high log probability relative to the true distribution. This is because in a quite literal sense, the true distribution is just the distribution over what humans actually write.
A current SOTA model, by contrast, is likely to write something with an extremely low log probability, most likely because it will write something that lacks long-term coherence, and is inhuman, and thus, won’t be something that would ever appear in the true distribution (or if it appears, it appears very very very rarely).
The last two points provide strong evidence that humans are actually better at the long-sequence task than SOTA models, even though they’re worse at the next character task.
Intuitively, this is because the SOTA model loses a gigantic amount of log probability when it generates whole sequences that no human would ever write. This doesn’t happen on the next character prediction task because you don’t need a very good understanding of long-term coherence to predict the vast majority of next-characters, and this effect dominates the effect from a lack of long-term coherence in the next-character task.
It is true (and I didn’t think of this before) that the human’s cross entropy score will probably be really high purely because they won’t even think to have any probability on some types of sequences that appear in the true distribution. I still don’t think this makes them worse than SOTA language models because the SOTA will also have ~0 probability on nearly all actual sequences. However…
Even if you aren’t convinced by my last argument, I can simply modify what I mean by the “true distribution” to mean the “true distribution of texts that are in the reference class of things we care about”. There’s absolutely no reason to say the true distribution has to be “everything on the internet” as opposed to “all books” or even “articles written by Rohin” if that’s what we’re actually trying to model.
Thus, I don’t accept one of your premises. I expect current language models to be better than you at next-character prediction on the empirical distribution of Rohin articles, but worse than you at whole sequence prediction for Rohin articles, for reasons you seem to already accept.
If I had to pick a claim to disagree with it would be the one about the "true distribution", but it's less that I disagree with the claim, and more that I disagree with using this particular method for declaring whether AIs are superhuman at language modeling.
but worse than you at whole sequence prediction for Rohin articles, for reasons you seem to already accept.
But a model can never be better than me at this task! Why are we interested in it?
This really feels like the core issue: if you define a task as "sample accurately from distribution D", and you define the distribution D as "whatever is produced by X", then X is definitionally optimal at the task, and no AI system is ever going to be super-X.
(Even once the AI system can fool humans into thinking its text is human-generated, there could still something inhuman about it that the humans fail to pick up on, that means that its generations are near-zero probability.)
In the language modeling case it isn't quite this perverse (because we the distribution is "whatever is produced by all humans" whereas we're only asking the AI to be better than one human) but it still seems pretty perverse.
I think a better evaluation of human ability at language modeling would be (1) sampling a sequence from the empirical dataset, (2) sampling a sequence from a human, (3) evaluate how often these two are the same, (4) do some math to turn this into a perplexity. This would have huge variance (obviously most of the time the sequences won't be the same for step (3)), but you can reduce the variance by sampling continuations for a given prompt rather than sampling sequences unprompted, and reduce it further by looking just at sampling the next token given a prompt (at which point you are at the scheme used in this post).
I still don’t think this makes them worse than SOTA language models because the SOTA will also have ~0 probability on nearly all actual sequences.
On my view, this is just the sum of log probs on next tokens, so presumably the result from this post implies that the language model will be way better than humans (while still assigning very low probability to a given sequence, just because the sequence is long, similarly to how you would assign very low probability to any given long sequence of coin flips).
However, I'm still not sure how exactly you are thinking of "the probability assigned by the human" -- it seems like you don't like the methodology of this post, but if not that, I don't see how else you would elicit a probability distribution over tokens / words / sequences from humans, and so I'm not really sure how to ground this claim.
(Whereas I think I do understand your claims about what kinds of text humans tend to generate.)
Building on this comment, I think it might be helpful for readers to make a few distinctions in their heads:
If you want to play with our website, it’s here; in our opinion playing this game for half an hour gives you some useful perspective on what it’s like to be a language model.
Wow that's fun! And quite frustrating. The worst is when I make such a near miss. Here are some pairs from my third document, with the first being my guess, and the latter being the correct token
Overall I'm getting like 20%, or worse, on these things. I played for ~20 mins, seems like there are obvious improvements to be found in my strategies. Obviously it gets easier as the essays go on, when you have narrowed in further on who the author is and why they're writing. Seems like ML systems can get ~49%, that's pretty incredible.
Here is the website where participants played the game.
And there's a second game! I found this one more fun than the first, I guess because the action space was less vast.
It's fun how even when I'm right I sometimes don't get points, because the model I'm competing with also predicted correctly (e.g. one time I predicted something with 99% confidence, and only got +2, because it was also obvious to the model).
Wow my score was terrible, only 175, compared to 921 for the 2-layers model.
This is very valuable. I suggest putting this content on Arxiv (even it's less formal that the typical paper).
Curated.
I am unsure how obvious this result is in-advance, my guess is there are at least some people who would have correctly predicted it and for the right reasons. However, I really love a lot of things about this post: first because you answer a question ML researchers do have disagreements over, second because you coded two small games for humans to play to help understand what's going on, third because you collect novel data, and fourth because you present it so clearly and readably.
I gained a better understanding of how language-models work from reading this post and playing the games, and I'd love to see more posts answering open questions through this kind of simple experimental work.
Playing the perplexity game had a big impact on my intuitions around language models, so thanks for making it! In particular, the fact that models are so much better at it than humans means we can't really tell from behavior alone whether a model is genuinely trying to predict the next token. This is a problem for detecting inner alignment failure, because we can't tell (outside of the training set) if the model is actually optimizing for next-token prediction or something that just looks (to us) like next-token prediction.
Playing this game made me realize that humans aren't trainged to predict at the token-level. I don't know the token-level vocabulary; and made lots of mistakes by missing spaces and punctuation. Is it possible to convert the token-level prediction in to word-level prediction? This may get you a better picture of human ability.
One way to convert: measure how accurate the LM is at word-level prediction by measuring its likelihood of each possible word. For example the LM's likelihood of the word "[token A][token B]" could be .
[Thanks to a variety of people for comments and assistance (especially Paul Christiano, Nostalgebraist, and Rafe Kennedy), and to various people for playing the game. Buck wrote the top-1 prediction web app; Fabien wrote the code for the perplexity experiment and did most of the analysis and wrote up the math here, Lawrence did the research on previous measurements. Epistemic status: we're pretty confident of our work here, but haven't engaged in a super thorough review process of all of it--this was more like a side-project than a core research project.]
How good are modern language models compared to humans, at the task language models are trained on (next token prediction on internet text)? While there are language-based tasks that you can construct where humans can make a next-token prediction better than any language model, we aren't aware of any apples-to-apples comparisons on non-handcrafted datasets. To answer this question, we performed a few experiments comparing humans to language models on next-token prediction on OpenWebText.
Contrary to some previous claims, we found that humans seem to be consistently worse at next-token prediction (in terms of both top-1 accuracy and perplexity) than even small models like Fairseq-125M, a 12-layer transformer roughly the size and quality of GPT-1. That is, even small language models are "superhuman" at predicting the next token. That being said, it seems plausible that humans can consistently beat the smaller 2017-era models (though not modern models) with a few hours more practice and strategizing. We conclude by discussing some of our takeaways from this result.
We're not claiming that this result is completely novel or surprising. For example, FactorialCode makes a similar claim as an answer on this LessWrong post about this question. We've also heard from some NLP people that the superiority of LMs to humans for next-token prediction is widely acknowledged in NLP. However, we've seen incorrect claims to the contrary on the internet, and as far as we know there hasn't been a proper apples-to-apples comparison, so we believe there's some value to our results.
If you want to play with our website, it’s here; in our opinion playing this game for half an hour gives you some useful perspective on what it’s like to be a language model.
Previous claims and related work
One commonly cited source for human vs LM next-token prediction performance is this slide from Steve Omohundro’s GPT-3 presentation, where he claims that humans have perplexity ~12, compared to GPT-3’s 20.5. (Smaller perplexity means you're better at predicting.)
This comparison is problematic for two reasons, one small and one fatal. The smaller problem is that the language model statistics are word-level perplexities computed on Penn Tree Bank (PTB), while the Human perplexity is from Shen et al 2017, which estimated the word-level perplexity on the 1 Billion Words (IBW) benchmark. This turns out not to matter much, as while GPT-3 was not evaluated on 1BW, GPT-2 performs slightly worse on 1BW than PTB. The bigger issue is the methodology used to estimate human perplexity: Shen et al asked humans to rate sentences on a 0-3 scale, where 0 means “clearly inhuman” and “3” was clearly human, then computed a “human judgment score” consisting of the ratio of sentences rated 3 over those rated 0. They then fit a degree-3 polynomial regression to the LMs they had (of which the best was a small LSTM), which they extrapolated significantly out of distribution to acquire the “human” perplexity:
This methodology is pretty dubious for several reasons, and we wouldn’t put much stock into the “humans have 12 perplexity” claim.
Another claim is from OpenAI regarding the LAMBADA dataset, where they give a perplexity of “~1-2” for humans (compared to 3.0 for 0-shot GPT-3). However, the authors don’t cite a source. As Gwern notes, the authors of the blog post likely made an educated guess based on how the LAMBADA dataset was constructed. In addition, LAMBADA is a much restricted dataset, which consists of guessing single words requiring broad context. So this comparison isn’t very informative to the question of how good language models are at the task they’re trained on–predicting the next token on typical internet text.
The only study we know of which tried to do something closely analogous is Goldstein 2020 (a neuroscience paper), which found that an ensemble of 50 humans have a top-1 accuracy of 28% vs 36% for GPT-2, which is similar to what we saw for humans on webtext. However, they used a different dataset (this transcript), which is not particularly representative of randomly-sampled English internet text.
There’s certainly a lot of more narrow datasets on which we have both human and LM performance, where humans significantly outperform LMs. For example, Hendrycks et al’s MATH dataset. But we couldn’t find an apples-to-apples comparison between humans and modern LMs for webtext next-token prediction.
How to measure human performance at next-token prediction?
The main difficulty for comparing human vs LM performance is that, unlike with language models, it’s infeasible for humans to give their entire probability distribution for the next token in a sequence (as there are about fifty thousand tokens). We tried two approaches to get around this.
The first one is to ask humans what token is most likely to come next. Using this method, you can’t get humans’ perplexity, but top-1 accuracy might still give us a reasonable measure of how well humans do at next token prediction. According to this measure, humans are worse than all (non-toy) language models we tried, even if you use really smart humans who have practiced for more than an hour.
We tried a different approach to get a measurement of human perplexity: humans were asked to rate the relative probability of two different tokens. If many humans answer this question on the same prompt, you can estimate the probability of the correct token according to humans, and thus estimate human perplexity. As with the top-1 accuracy metric, humans score worse according to this perplexity estimator than all language models we tried, even a toy 2-layer model.
Top-1 accuracy evaluation
Method
We measured human top-1 accuracy: that is, they had to guess the single token that they thought was most likely to come next, and we measured how often that token in fact came next. Humans were given the start of a random OpenWebText document, and they were asked to guess which token comes next. Once they had guessed, the true answer was revealed (to give them the opportunity to get better at the game), and they were again asked to guess which token followed the revealed one.
Here is the website where participants played the game. We recommend playing the game if you want to get a sense of what next-token prediction is like.
The participants were either staff/advisors of Redwood Research, or members of the Bountied Rationality Facebook group, paid $30/hour.
Results
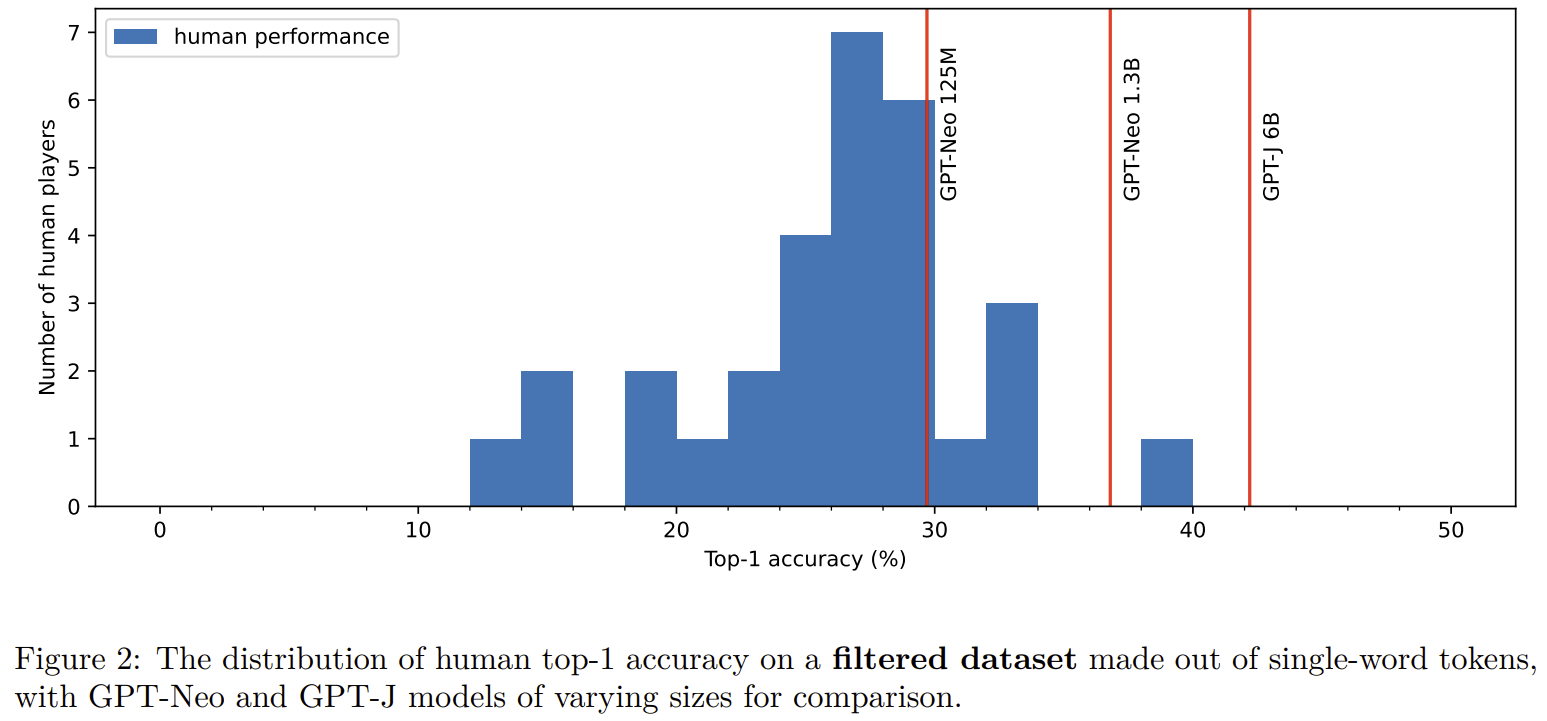
60 participants played the game, making a total of 18530 guesses. The overall accuracy of their answers on this top-1 task was 29%. Of these players, 38 gave at least 50 answers, with an accuracy of 30%. This accuracy is low compared to the accuracy of large language models: when measured on the same dataset humans were evaluated on, GPT-3 got an accuracy of 49% and even the 125M parameters fairseq model got an accuracy above the accuracy of all but one player in our dataset (who guessed 70 tokens), as you can see in the graph below (though it seems possible that with practice humans might be able to beat fairseq-125M reliably).
7 players guessed over 500 tokens, getting accuracies around the average of human performance (0.26, 0.26, 0.27, 0.28, 0.31, 0.31, 0.32), which indicates that humans don’t quickly get much higher performance with five hours of training.
Some of these scores are from Redwood Research staff and advisors who we think were very motivated to try hard and do well, so we don’t think that this is an artifact of our participants being weak.
Some participants wrote up notes on the experience, describing their strategies and what was easy/hard. Links: William Kiely, Marcus.
This website didn’t have any way for humans to guess newlines or some other visually-empty tokens, and we excluded cases where the correct guess was impossible from the above analysis.
To sum up, humans have only barely beat 2017-era language models, and humans are much worse than modern ones at top-1 token prediction.
Human perplexity evaluation
(Thanks to Paul Christiano for suggesting the rough approach here, and to Paul and Adam Scherlis for helping with some of the details.)
But language models aren’t trained to guess the single most likely next token, and so the previous task isn’t actually directly assessing the language models on the task they’re trained on. They’re trained to give a full distribution over next tokens, aiming to minimize their perplexity (aka minimizing log loss; perplexity is a measure of how well a probability distribution predicts a sample). It’s easy to calculate the model’s perplexity, because the models produce a probability for every next token. Unfortunately, humans aren’t able to quickly provide a probability distribution over the fifty thousand possible tokens. So if we want to measure human perplexity, we’ll have to do it indirectly.
Method
The method we ended up using is complicated and messy, and though it’s a fun exercise in probability theory, it is probably not worth your time to understand if you just want to know about human performance on language modeling.
For a given prompt sampled from the validation dataset of OpenWebText, we make the dubious assumption that all humans have exactly the same probability distribution over next tokens, and then infer the probability that humans assign to the correct token by showing many humans different choices between the correct next token and another random token, and then asking them for the probability that the left one is the correct token.
We used importance sampling and comparison with a reference language model to reduce the variance of the estimator (details in Appendix A). This importance sampling scheme allows the human to update on the probability that a token is the true next token based on the fact that they’re being asked about it. So we came up with a scoring rule, detailed in Appendix B and explained on the website, which incentivizes people to state their true probabilities before updating on which tokens they’d been asked to compare.
Here is the website where participants played the game.
The participants were again either staff of Redwood Research or members of the Bountied Rationality Facebook group paid $15 for answering a set of comparisons (which takes ~30 minutes, taking into account a bit of training). The first set consists of 40 questions from different texts (you can take it here). The second set consists of 80 comparisons from 8 different texts (you can take it here).
Note: prompts are chosen to be at most 120 tokens long in order to spare human reading time, and always start at the beginning of the text. Models are evaluated on the same dataset.
Results
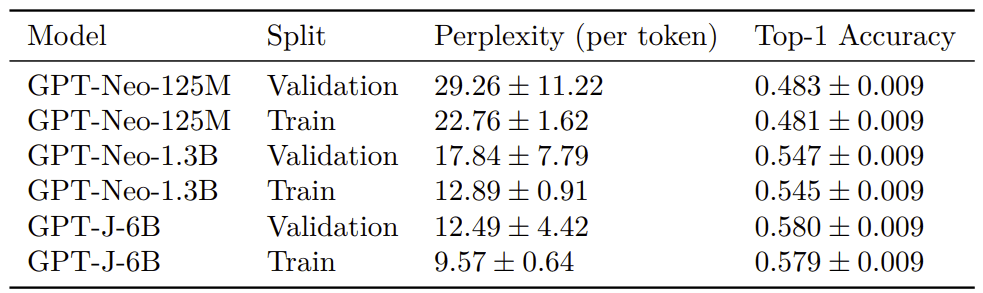
19 participants answered all 40 questions of the first set, and 11 participants answered all 80 questions of the second set, answering a total of 1640 comparisons. This was enough to conclude that human are worse than language models, as you can see in the graph below:
Human and language model performance are then compared exactly on the same comparison. As our human participants could only enter one of the 11 ratios in our interface, we also report the “rounded” performance of our LMs - that is, the performance of our LMs if they choose the checkbox that is the closest to their probability ratio. (Note that we can’t access the true perplexity of rounded models as only ratios are rounded and not the probability of the correct token.)
As explained in Appendix A, the loss obtained by this method is usually an underestimation of the true loss you would get if you asked infinitely many questions, because the sum used to do the estimations is heavily tailed. The displayed (2 standard error) uncertainty intervals represents “where would the estimation be if we did the experiment a second time with different samples”, rather than “where is the true value of human loss” (which would probably be above the upper bound of the interval). GPT-2 small is used as the generator, which is why its measured perplexity using the estimator is perfect. More details about the uncertainty estimation can be found in Appendix C.
But this method could also overestimate human perplexity: there could be other setups in which it would be easier for players to give calibrated probabilities. In fact, some players found the scoring system hard to understand, and if it led them to not express their true probability ratios, we might have underestimated human performance. In general, this method is very sensitive to failures at giving calibrated probability estimates: the high perplexity obtained here is probably partially due to humans being bad at giving calibrated probabilities, rather than humans just being bad at language modeling. In addition, as humans are restricted to one of 11 ratios, our setup could also underestimate performance by artificially reducing the resolution of our human participants.
Thus, while we don’t have a good way to precisely measure human perplexity, these results give reasonable evidence that it is high. In particular, humans are worse than a two-layer model at giving calibrated estimates of token vs token probabilities.
It's worth noting that our results are not consistent with the classic result from Shannon 1950, which estimated the the average per-character entropy to be between 0.6 and 1.3 bits, corresponding to a per-token perplexity between 7 and 60 (as the average length of tokens in our corpus is 4.5). This is likely due to several reasons. First, as noted above, our setup may artificially increase the estimated perplexity due to our human subjects being uncalibrated and our interface rounding off probability ratios. In addition, Shannon used his wife Mary Shannon and the HP Founder Barnard Oliver as his subjects, who may be higher quality than our subjects or have spent more time practicing on the task. [EDIT: as Matthew Barnett notes in a comment below, our estimate of human perplexity is consistent with other estimates performed after Shannon.] Finally, he used a different dataset (excerpts from Dumas Malne's Jefferson the Virginian, compared to our OpenWebText excerpts).
Conclusion
The results here suggest that humans are worse than even small language models the size of GPT-1 at next-token prediction, even on the top-1 prediction task. This seems true even when the humans are smart and motivated and have practiced for an hour or two. Some humans can probably consistently beat GPT-1, but not substantially larger models, with a bit more practice.
What should we take away from this?
Appendix A: How to estimate human loss with importance sampling
Let T be the true distribution of tokens y after a context c. The loss of a human is defined to be the average -log probability of the true token according to the human probabilities h over the next token: L=−E(C,Y)∼Tlogh(Y|C)
However, we can’t directly ask a human what the probability of the true token is (without spoiling them on the answer), and it would be very cumbersome to ask for their whole probability distribution. We can do better by asking for relative likelihoods: for a given context c and true token y, because ∑xp(x|c)=1, −logh(y|c)=log∑xh(x/c)/h(y|c).
That’s better, but that would still be around 50,000 questions (the number of tokens) per token. To lower this number, we use importance sampling: the bulk of ∑h(x/c)/h(y|c) is where the most likely tokens are, so it’s not worth asking for every one of them. To do that, we condition a language model G on our context C from which we can sample the most likely tokens, and we use the following approximation:
∑all tokensxh(x/c)/h(y|c)=EX∼Gc(h(X|c)h(y|c)g(X|c)) ≈1n∑x∼Gch(x|c)h(y|c)g(x|c) for an that can be much smaller than 50,000. for an n that can be much smaller than 50,000.
To decrease the variance of this estimator (and thereby increase the quality of the estimation), instead of estimating h(y|c) we estimate h(y|c)g(y|c)=EX∼Gc(h(X|c)g(y|c)h(y|c)g(X|c)) ≈1n∑x∼Gch(x|c)g(y|c)h(y|c)g(x|c). The variance is lower because, if h and g are close, h(x|c)g(y|c)h(y|c)g(x|c) will most of the time be close to 1, whereas h(x|c)h(y|c)g(x|c) can get very large on some samples.
Thanks to the properties of log, L−LG=−E(C,Y)∼Tlogh(Y|C)g(Y|C) (where LG is the loss of G, defined in the same way as L but using g instead of h).
Using N samples from the true target corpus, we get
L−LG≈1N∑(c,y)∼Tlog(1n∑x∼Gch(x|c)g(y|c)h(y|c)g(x|c))
In practice, we use GPT-2 small - a 12-layer language model - as our generator language model.
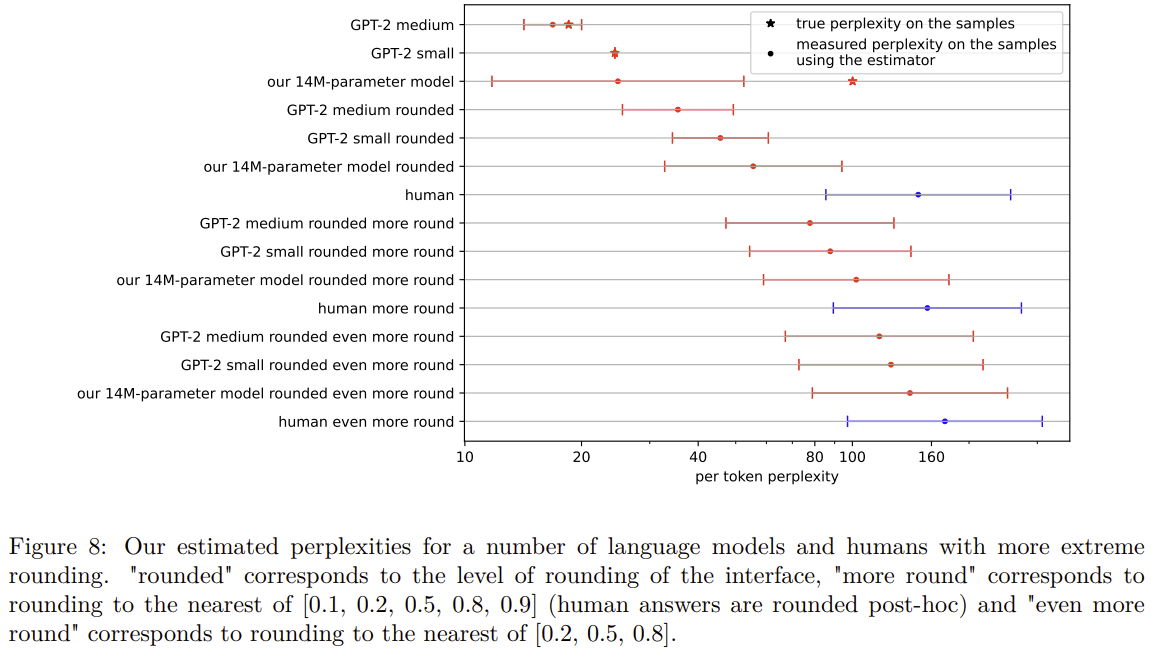
Using this method to measure the loss of a 2-layer LM and a 24-layer LM using a 12-layer LM as a generator, we find that this method underestimates of the true loss of the ground truth, and that the results is at most 0.5 bits away from the ground truth when n≈40, for models that are very dissimilar (like 2-layer model vs 12-layer LM, which the difference in true loss is 1.3 bits). This is a large difference, but this is still good enough for the purpose of comparing humans to language models (because humans are terrible language models). The difference can be explained by the fact that the sum over x is heavy tailed toward +∞: if you don’t sample enough, your empirical mean will often be below the true expected value.
Appendix B: How to get human relative likelihoods
We want to get h(x|c)/h(y|c), the relative likelihood of tokens x and y in a given context C according to a human. This might seem easy: just make the human guess if the prompt c is followed by x or y, and then the human should answer that c is followed by x with probability h(x|c)h(y|c)+h(y|c). This would be true if one token was sampled from the true distribution and the other one was selected uniformly between all other tokens. However, this doesn’t work if in this case because the other token is sampled from Gc: a rational agent that perfectly knows the true distribution T and the generated distribution G would answer that c is followed by x with probability
P(x∼Tc∧y∼Gc)P(x∼Tc∧y∼Gc)+P(x∼Gc∧y∼Tc)
=t(x|c)g(y|c)t(y|c)g(x|c)+t(x|c)g(y|c) (because of the independence of Tc & Gc).
Thus, if you believe Tc to get indistinguishable from Gc, a human will answer “0.5” to every question, making it impossible to extract h(x|c)/h(y|c).
The solution to get h(x|c)/h(y|c) is to incentivize the human to give something else than their best guess. We ask the human for the probability p that c is followed by x, and we reward them with a weighted binary cross entropy reward R(p)=g(x|c)log(p)1z=x+g(y|c)log(1−p)1z=y where z is the correct answer. The expected value of this reward, according to a human believing that the generative follows a distribution ^G, is E(R(p))=^g(x|c)log(p)(h(x|c)^g(y|c))+^g(y|c)log(1−p)(h(y|c)^g(x|c)) which is at its maximum when dE(R(p))dp=0, therefore, the optimal play satisfies ^g(x|c)^g(y|c)h(x|c)/p∗=^g(y|c)^g(x|c)h(y|c)/(1−p∗), hence p∗=h(x|c)h(y|c)+h(x|c). From this, we get h(y|c)/h(x|c)=1p∗−1. Assuming human play optimally (which is a questionable assumption), we are able to get their true probability ratios, no matter what their beliefs about the generative model are.
Note: in practice we use a slightly different reward R(p)=1000(g(x|c)(log(p)−log(0.5))1z=x+g(y|c)(log(1−p)−log(0.5))1z=y for which the optimal play is the same, but which is more understandable for human: one always gets a reward of 0 for saying “I don’t know”, and the scaling makes things more readable.
Note 2: when x=y the human isn't asked to compare their relative likelyhoods. Instead, the website automatically answers that both are as likely.
Appendix C: estimating uncertainties in human perplexity
If we assume humans play rationally in the game described above, there remains three sources of uncertainty in our measurement of human perplexity:
Uncertainties 1 & 3 are hard to combine, and because 3 is small compared to 1, we chose to use only the first one.
Here is the same graph as shown in the result section, but using only the uncertainties measured using technique 3.