There’s a useful intuitive notion of “optimization” as pushing the world into a small set of states, starting from any of a large number of states. Visually:
Yudkowsky and Flint both have notable formalizations of this “optimization as compression” idea.
This post presents a formalization of optimization-as-compression grounded in information theory. Specifically: to “optimize” a system is to reduce the number of bits required to represent the system state using a particular encoding. In other words, “optimizing” a system means making it compressible (in the information-theoretic sense) by a particular model.
This formalization turns out to be equivalent to expected utility maximization, and allows us to interpret any expected utility maximizer as “trying to make the world look like a particular model”.
Conceptual Example: Building A House
Before diving into the formalism, we’ll walk through a conceptual example, taken directly from Flint’s Ground of Optimization: building a house. Here’s Flint’s diagram:
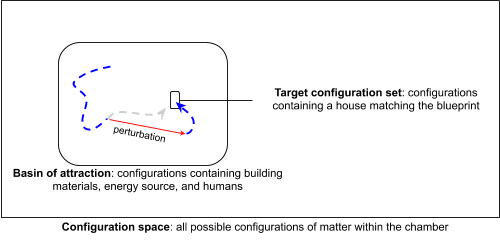
The key idea here is that there’s a wide variety of initial states (piles of lumber, etc) which all end up in the same target configuration set (finished house). The “perturbation” indicates that the initial state could change to some other state - e.g. someone could move all the lumber ten feet to the left - and we’d still end up with the house.
In terms of information-theoretic compression: we could imagine a model which says there is probably a house. Efficiently encoding samples from this model will mean using shorter bit-strings for world-states with a house, and longer bit-strings for world-states without a house. World-states with piles of lumber will therefore generally require more bits than world-states with a house. By turning the piles of lumber into a house, we reduce the number of bits required to represent the world-state using this particular encoding/model.
If that seems kind of trivial and obvious, then you’ve probably understood the idea; later sections will talk about how it ties into other things. If not, then the next section is probably for you.
Background Concepts From Information Theory
The basic motivating idea of information theory is that we can represent information using fewer bits, on average, if we use shorter representations for states which occur more often. For instance, Morse code uses only a single bit (“.”) to represent the letter “e”, but four bits (“- - . -”) to represent “q”. This creates a strong connection between probabilistic models/distributions and optimal codes: a code which requires minimal average bits for one distribution (e.g. with lots of e’s and few q’s) will not be optimal for another distribution (e.g. with few e’s and lots of q’s).
For any random variable generated by a probabilistic model , we can compute the minimum average number of bits required to represent . This is Shannon’s famous entropy formula
Assuming we’re using an optimal encoding for model , the number of bits used to encode a particular value is . (Note that this is sometimes not an integer! Today we have algorithms which encode many samples at once, potentially even from different models/distributions, to achieve asymptotically minimal bit-usage. The “rounding error” only happens once for the whole collection of samples, so as the number of samples grows, the rounding error per sample goes to zero.)
Of course, we could be wrong about the distribution - we could use a code optimized for a model which is different from the “true” model . In this case, the average number of bits used will be
In this post, we’ll use a “wrong” model intentionally - not because we believe it will yield short encodings, but because we want to push the world into states with short -encodings. The model serves a role analogous to a utility function. Indeed, we’ll see later on that every model is equivalent to a utility function, and vice-versa.
Formal Statement
Here are the variables involved in “optimization”:
- World-state random variables
- Parameters which will be optimized
- Probabilistic world-model representing the distribution of
- Probabilistic world-model representing the encoding in which we wish to make more compressible
An “optimizer” takes in some parameter-values , and returns new parameter-values such that
… with equality if-and-only-if already achieves the smallest possible value. In English: we choose to reduce the average number of bits required to encode a sample from , using a code optimal for . This is essentially just our formula from the previous section for the number of bits used to encode a sample from using a code optimal for .
Other than the information-theory parts, the main thing to emphasize is that we’re mapping one parameter-value to a “more optimal” parameter-value . This should work for many different “initial” -values, implying a kind of robustness to changes in . (This is roughly the same concept which Flint captured by talking about “perturbations” to the system-state.) In the context of iterative optimizers, our definition corresponds to one step of optimization; we could of course feed back into the optimizer and repeat. We could even do this without having any distinguished “optimizer” subsystem - e.g. we might just have some dynamical system in which is a function of time, and successive values of satisfy the inequality condition.
Finally, note that our model is a function of . This form is general enough to encompass all the usual decision theories. For instance, under EDT, would be some base model conditioned on the data . Under CDT, would instead be a causal intervention on a base model , i.e. .
Equivalence to Expected Utility Optimization
Obviously our expression can be expressed as an expected utility: just set . The slightly more interesting claim is that we can always go the other way: for any utility function , there is a corresponding model , such that maximizing expected utility is equivalent to minimizing expected bits to encode using .
The main trick here is that we can always add a constant to , or multiply by a positive constant, and it will still “be the same utility” - i.e. an agent with the new utility will always make the same choices as the old. So, we set
… and look for which give us a valid probability distribution (i.e. all probabilities are nonnegative and sum to 1).
Since everything is in an exponent, all our probabilities will be nonnegative for any , so that constraint is trivially satisfied. To make the distribution sum to one, we simply set . So, not only can we find a model for any , we actually find a whole family of them - one for each .
(This also reveals a degree of freedom in our original definition: we can always create a new model with without changing the behavior.)
So What Does This Buy Us?
If this formulation is equivalent to expected utility maximization, why view it this way?
Intuitively, this view gives more semantics to our “utility functions”. They have built-in “meanings”; they’re not just preference orderings.
Mathematically, the immediately obvious step for anyone with an information theory background is to write:
The expected number of bits required to encode using is the entropy of plus the Kullback-Liebler divergence of (distribution of under model ) from (distribution of under model ). Both of those terms are nonnegative. The first measures “how noisy” is, the second measures “how close” the distributions are under our two models.
Intuitively, this math says that we can decompose the objective into two pieces:
- Make more predictable
- Make the distribution of “close to” the distribution , with closeness measured by KL-divergence
Combined with the previous section: we can take any expected utility maximization problem, and decompose it into an entropy minimization term plus a “make-the-world-look-like-this-specific-model” term.
This becomes especially interesting in situations where the entropy of cannot be reduced - e.g. thermodynamics. If the entropy is fixed, then only the KL-divergence term remains. In this case, we can directly interpret the optimization problem as “make the world-state distribution look like ”. If we started from an expected utility optimization problem, then we derive a model such that optimizing expected utility is equivalent to making the world look as much as possible like .
In fact, even when is not fixed, we can build equivalent models for which it is fixed, by adding new variables to . Suppose, for example, that we can choose between flipping a coin and rolling a die to determine . We can change the model so that both the coin flip and the die roll always happen, and we include their outcomes in . We then choose whether to set equal to the coin flip result or the die roll result, but in either case the entropy of is the same, since both are included. simply ignores all the new components added to (i.e. it implicitly has a uniform distribution on the new components).
So, starting from an expected utility maximization problem, we can transform to an equivalent minimum coded bits problem, and from there to an equivalent minimum KL-divergence problem. We can then interpret the optimization as “choose to make as close as possible to ”, with closeness measured by KL-divergence.
What I Imagine This Might Be Useful For
In general, interpretations of probability grounded in information theory are much more solid than interpretations grounded in coherence theorems. However, information-theoretic groundings only talk about probability, not about "goals" or "agents" or anything utility-like. Here, we've transformed expected utility maximization into something explicitly information-theoretic and conceptually natural. This seems like a potentially-promising step toward better foundations of agency. I imagine there's probably purely-information-theoretic "coherence theorems" to be found.
Another natural direction to take this in is thermodynamic connections, e.g. combining it with a generalized heat engine. I wouldn't be surprised if this also tied in with information-theoretic "coherence theorems" - in particular, I imagine that negentropy could serve as a universal "resource", replacing the "dollars" typically used as a measuring stick in coherence theorems.
Overall, the whole formulation smells like it could provide foundations much more amenable to embedded agency.
Finally, there's probably some nice connection to predictive processing. In all likelihood, Karl Friston has already said all this, but it has yet to be distilled and disseminated to the rest of us.