Planned summary for the Alignment Newsletter:
Once again, we have a piece of work so large and detailed that I need a whole newsletter to summarize it! This time, it is a quantitative model for forecasting when transformative AI will happen.
The overall framework
The key assumption behind this model is that if we train a neural net or other ML model that uses about as much computation as a human brain, that will likely result in transformative AI (TAI) (defined as AI that has an impact comparable to that of the industrial revolution). In other words, we _anchor_ our estimate of the ML model’s inference computation to that of the human brain. This assumption allows us to estimate how much compute will be required to train such a model _using 2020 algorithms_. By incorporating a trend extrapolation of how algorithmic progress will reduce the required amount of compute, we can get a prediction of how much compute would be required for the final training run of a transformative model in any given year.
We can also get a prediction of how much compute will be _available_ by predicting the cost of compute in a given year (which we have a decent amount of past evidence about), and predicting the maximum amount of money an actor would be willing to spend on a single training run. The probability that we can train a transformative model in year Y is then just the probability that the compute _requirement_ for year Y is less than the compute _available_ in year Y.
The vast majority of the report is focused on estimating the amount of compute required to train a transformative model using 2020 algorithms (where most of our uncertainty would come from); the remaining factors are estimated relatively quickly without too much detail. I’ll start with those so that you can have them as background knowledge before we delve into the real meat of the report. These are usually modeled as logistic curves in log space: that is, they are modeled as improving at some constant rate, but will level off and saturate at some maximum value after which they won’t improve.
Algorithmic progress
First off, we have the impact of _algorithmic progress_. <@AI and Efficiency@> estimates that algorithms improve enough to cut compute times in half every 16 months. However, this was measured on ImageNet, where researchers are directly optimizing for reduced computation costs. It seems less likely that researchers are doing as good a job at reducing computation costs for “training a transformative model”, and so the author increases the **halving time to 2-3 years**, with a maximum of **somewhere between 1-5 orders of magnitude** (with the assumption that the higher the “technical difficulty” of the problem, the more algorithmic progress is possible).
Cost of compute
Second, we need to estimate a trend for compute costs. There has been some prior work on this (summarized in [AN #97](https://mailchi.mp/a2b5efbcd3a7/an-97-are-there-historical-examples-of-large-robust-discontinuities)). The report has some similar analyses, and ends up estimating **a doubling time of 2.5 years**, and a (very unstable) maximum of improvement by **a factor of 2 million by 2100**.
Willingness to spend
Third, we would like to know the maximum amount (in 2020 dollars) any actor might spend on a single training run. Note that we are estimating the money spent on a _final training run_, which doesn’t include the cost of initial experiments or the cost of researcher time. Currently, the author estimates that all-in project costs are 10-100x larger than the final training run cost, but this will likely go down to something like 2-10x, as the incentive for reducing this ratio becomes much larger.
The author estimates that the most expensive run _in a published paper_ was the final <@AlphaStar@>(@AlphaStar: Mastering the Real-Time Strategy Game StarCraft II@) training run, at ~1e23 FLOP and $1M cost. However, there have probably been unpublished results that are slightly more expensive, maybe $2-8M. In line with <@AI and Compute@>, this will probably increase dramatically to about **$1B in 2025**.
Given that AI companies each have around $100B cash on hand, and could potentially borrow additional several hundreds of billions of dollars (given their current market caps and likely growth in the worlds where AI still looks promising), it seems likely that low hundreds of billions of dollars could be spent on a single run by 2040, corresponding to a doubling time (from $1B in 2025) of about 2 years.
To estimate the maximum here, we can compare to megaprojects like the Manhattan Project or the Apollo program, which suggests that a government could spend around 0.75% of GDP for ~4 years. Since transformative AI will likely be more valuable economically and strategically than these previous programs, we can shade that upwards to 1% of GDP for 5 years. Assuming all-in costs are 5x that of the final training run, this suggests the maximum willingness to spend should be 1% of GDP of the largest country, which we assume grows at ~3% every year.
Strategy for estimating training compute for a transformative model
In addition to the three factors of algorithmic progress, cost of compute, and willingness to spend, we need an estimate of how much computation would be needed to train a transformative model using 2020 algorithms (which I’ll discuss next). Then, at year Y, the compute required is given by computation needed with 2020 algorithms * improvement factor from algorithmic progress, which (in this report) is a probability distribution. At year Y, the compute available is given by FLOP per dollar (aka compute cost) * money that can be spent, which (in this report) is a point estimate. We can then simply read off the probability that the compute required is greater than the compute available.
Okay, so the last thing we need is a distribution over the amount of computation that would be needed to train a transformative model using 2020 algorithms, which is the main focus of this report. There is a lot of detail here that I’m going to elide over, especially in talking about the _distribution_ as a whole (whereas I will focus primarily on the median case for simplicity). As I mentioned early on, the key hypothesis is that we will need to train a neural net or other ML model that uses about as much compute as a human brain. So the strategy will be to first translate from “compute of human brain” to “inference compute of neural net”, and then to translate from “inference compute of neural net” to “training compute of neural net”.
How much inference compute would a transformative model use?
We can talk about the rate at which synapses fire in the human brain. How can we convert this to FLOP? The author proposes the following hypothetical: suppose we redo evolutionary history, but in every animal we replace each neuron with N [floating-point units](https://en.wikipedia.org/wiki/Floating-point_unit) that each perform 1 FLOP per second. For what value of N do we still get roughly human-level intelligence over a similar evolutionary timescale? The author then does some calculations about simulating synapses with FLOPs, drawing heavily on the <@recent report on brain computation@>(@How Much Computational Power It Takes to Match the Human Brain@), to estimate that N would be around 1-10,000, which after some more calculations suggests that the human brain is doing the equivalent of 1e13 - 1e16 FLOP per second, with **a median of 1e15 FLOP per second**, and a long tail to the right.
Does this mean we can say that a transformative model will use 1e15 FLOP per second during inference? Such a model would have a clear flaw: even though we are assuming that algorithmic progress reduces compute costs over time, if we did the same analysis in e.g. 1980, we’d get the _same_ estimate for the compute cost of a transformative model, which would imply that there was no algorithmic progress between 1980 and 2020! The problem is that we’d always estimate the brain as using 1e15 FLOP per second (or around there), but for our ML models there is a difference between FLOP per second _using 2020 algorithms_ and FLOP per second _using 1980 algorithms_. So how do we convert form “brain FLOP per second” to “inference FLOP per second for 2020 ML algorithms”?
One approach is to look at how other machines we have designed compare to the corresponding machines that evolution has designed. An [analysis](https://docs.google.com/document/d/1HUtUBpRbNnnWBxiO2bz3LumEsQcaZioAPZDNcsWPnos/edit) by Paul Christiano concluded that human-designed artifacts tend to be 2-3 orders of magnitude worse than those designed by evolution, when considering energy usage. Presumably a similar analysis done in the past would have resulted in higher numbers and thus wouldn’t fall prey to the problem above. Another approach is to compare existing ML models to animals with a similar amount of computation, and see which one is subjectively “more impressive”. For example, the AlphaStar model uses about as much computation as a bee brain, and large language models use somewhat more; the author finds it reasonable to say that AlphaStar is “about as sophisticated” as a bee, or that <@GPT-3@>(@Language Models are Few-Shot Learners@) is “more sophisticated” than a bee.
We can also look at some abstract considerations. Natural selection had _a lot_ of time to optimize brains, and natural artifacts are usually quite impressive. On the other hand, human designers have the benefit of intelligent design and can copy the patterns that natural selection has come up with. Overall, these considerations roughly balance each other out. Another important consideration is that we’re only predicting what would be needed for a model that was good at most tasks that a human would currently be good at (think a virtual personal assistant), whereas evolution optimized for a whole bunch of other skills that were needed in the ancestral environment. The author subjectively guesses that this should reduce our estimate of compute costs by about an order of magnitude.
Overall, putting all these considerations together, the author intuitively guesses that to convert from “brain FLOP per second” to “inference FLOP per second for 2020 ML algorithms”, we should add an order of magnitude to the median, and add another two orders of magnitude to the standard deviation to account for our large uncertainty. This results in a median of **1e16 FLOP per second** for the inference-time compute of a transformative model.
Training compute for a transformative model
We might expect a transformative model to run a forward pass **0.1 - 10 times per second** (which on the high end would match human reaction time of 100ms), and for each parameter of the neural net to contribute **1-100 FLOP per forward pass**, which implies that if the inference-time compute is 1e16 FLOP per second then the model should have **1e13 - 1e17 parameters**, with a median of **3e14 parameters**.
We now need to estimate how much compute it takes to train a transformative model with 3e14 parameters. We assume this is dominated by the number of times you have to run the model during training, or equivalently, the number of data points you train on times the number of times you train on each data point. (In particular, this assumes that the cost of acquiring data is negligible in comparison. The report argues for this assumption; for the sake of brevity I won’t summarize it here.)
For this, we need a relationship between parameters and data points, which we’ll assume will follow a power law KP^α, where P is the number of parameters and K and α are constants. A large number of ML theory results imply that the number of data points needed to reach a specified level of accuracy grows linearly with the number of parameters (i.e. α=1), which we can take as a weak prior. We can then update this with empirical evidence from papers. <@Scaling Laws for Neural Language Models@> suggests that for language models, data requirements scale as α=0.37 or as α=0.74, depending on what measure you look at. Meanwhile, [Deep Learning Scaling is Predictable, Empirically](https://arxiv.org/abs/1712.00409) suggests that α=1.39 for a wide variety of supervised learning problems (including language modeling). However, the former paper studies a more relevant setting: it includes regularization, and asks about the number of data points needed to reach a target accuracy, whereas the latter paper ignores regularization and asks about the minimum number of data points that the model _cannot_ overfit to. So overall the author puts more weight on the former paper and estimates a median of α=0.8, though with substantial uncertainty.
We also need to estimate how many epochs will be needed, i.e. how many times we train on any given data point. The author decides not to explicitly model this factor since it will likely be close to 1, and instead lumps in the uncertainty over the number of epochs with the uncertainty over the constant factor in the scaling law above. We can then look at language model runs to estimate a scaling law for them, for which the median scaling law predicts that we would need 1e13 data points for our 3e14 parameter model.
However, this has all been for supervised learning. It seems plausible that a transformative task would have to be trained using RL, where the model acts over a sequence of timesteps, and then receives (non-differentiable) feedback at the end of those timesteps. How would scaling laws apply in this setting? One simple assumption is to say that each rollout over the _effective horizon_ counts as one piece of “meaningful feedback” and so should count as a single data point. Here, the effective horizon is the minimum of the actual horizon and 1/(1-γ), where γ is the discount factor. We assume that the scaling law stays the same; if we instead try to estimate it from recent RL runs, it can change the results by about one order of magnitude.
So we now know we need to train a 3e14 parameter model with 1e13 data points for a transformative task. This gets us nearly all the way to the compute required with 2020 algorithms: we have a ~3e14 parameter model that takes ~1e16 FLOP per forward pass, that is trained on ~1e13 data points with each data point taking H timesteps, for a total of H * 1e29 FLOP. The author’s distributions are instead centered at H * 1e30 FLOP; I suspect this is simply because the author was computing with distributions whereas I’ve been directly manipulating medians in this summary.
The last and most uncertain piece of information is the effective horizon of a transformative task. We could imagine something as low as 1 subjective second (for something like language modeling), or something as high as 1e9 subjective seconds (i.e. 32 subjective years), if we were to redo evolution, or train on a task like “do effective scientific R&D”. The author splits this up into short, medium and long horizon neural net paths (corresponding to horizons of 1e0-1e3, 1e3-1e6, and 1e6-1e9 respectively), and invites readers to place their own weights on each of the possible paths.
There are many important considerations here: for example, if you think that the dominating cost will be generative modeling (GPT-3 style, but maybe also for images, video etc), then you would place more weight on short horizons. Conversely, if you think the hard challenge is to gain meta learning abilities, and that we probably need “data points” comparable to the time between generations in human evolution, then you would place more weight on longer horizons.
Adding three more potential anchors
We can now combine all these ingredients to get a forecast for when compute will be available to develop a transformative model! But not yet: we’ll first add a few more possible “anchors” for the amount of computation needed for a transformative model. (All of the modeling so far has “anchored” the _inference time computation of a transformative model_ to the _inference time computation of the human brain_.)
First, we can anchor _parameter count of a transformative model_ to the _parameter count of the human genome_, which has far fewer “parameters” than the human brain. Specifically, we assume that all the scaling laws remain the same, but that a transformative model will only require 7.5e8 parameters (the amount of information in the human genome) rather than our previous estimate of ~1e15 parameters. This drastically reduces the amount of computation required, though it is still slightly above that of the short-horizon neural net, because the author assumed that the horizon for this path was somewhere between 1 and 32 years.
Second, we can anchor _training compute for a transformative model_ to the _compute used by the human brain over a lifetime_. As you might imagine, this leads to a much smaller estimate: the brain uses ~1e24 FLOP over 32 years of life, which is only 10x the amount used for AlphaStar, and even after adjusting upwards to account for man-made artifacts being worse than those made by evolution, the resulting model predicts a significant probability that we would already have been able to build a transformative model.
Finally, we can anchor _training compute for a transformative model_ to the _compute used by all animal brains over the course of evolution_. The basic assumption here is that our optimization algorithms and architectures are not much better than simply “redoing” natural selection from a very primitive starting point. This leads to an estimate of ~1e41 FLOP to train a transformative model, which is more than the long horizon neural net path (though not hugely more).
Putting it all together
So we now have six different paths: the three neural net anchors (short, medium and long horizon), the genome anchor, the lifetime anchor, and the evolution anchor. We can now assign weights to each of these paths, where each weight can be interpreted as the probability that that path is the _cheapest_ way to get a transformative model, as well as a final weight that describes the chance that none of the paths work out.
The long horizon neural net path can be thought of as a conservative “default” view: it could work out simply by training directly on examples of a long horizon task where each data point takes around a subjective year to generate. However, there are several reasons to think that researchers will be able to do better than this. As a result, the author assigns 20% to the short horizon neural net, 30% to the medium horizon neural net, and 15% to the long horizon neural net.
The lifetime anchor would suggest that we either already could get TAI, or are very close, which seems very unlikely given the lack of major economic applications of neural nets so far, and so gets assigned only 5%. The genome path gets 10%, the evolution anchor gets 10%, and the remaining 10% is assigned to none of the paths working out.
This predicts a **median of 2052** for the year in which some actor would be willing and able to train a single transformative model, with the full graphs shown below:
<Graphs removed since they are in flux and easy to share in a low-bandwidth way>
How does this relate to TAI?
Note that what we’ve modeled so far is the probability that by year Y we will have enough compute for the final training run of a transformative model. This is not the same thing as the probability of developing TAI. There are several reasons that TAI could be developed _later_ than the given prediction:
1. Compute isn’t the only input required: we also need data, environments, human feedback, etc. While the author expects that these will not be the bottleneck, this is far from a certainty.
2. When thinking about any particular path and making it more concrete, a host of problems tend to show up that will need to be solved and may add extra time. Some examples include robustness, reliability, possible breakdown of the scaling laws, the need to generate lots of different kinds of data, etc.
3. AI research could stall, whether because of regulation, a global catastrophe, an AI winter, or something else.
However, there are also compelling reasons to expect TAI to arrive _earlier_:
1. We may develop TAI through some other cheaper route, such as a <@services model@>(@Reframing Superintelligence: Comprehensive AI Services as General Intelligence@).
2. Our forecasts apply to a “balanced” model that has a similar profile of abilities as a human. In practice, it will likely be easier and cheaper to build an “unbalanced” model that is superhuman in some domains and subhuman in others, that is nonetheless transformative.
3. The curves for several factors assume some maximum after which progress is not possible; in reality it is more likely that progress slows to some lower but non-zero growth rate.
In the near future, it seems likely that it would be harder to find cheaper routes (since there is less time to do the research), so we should probably assume that the probabilities are overestimates, and for similar reasons for later years the probabilities should be treated as underestimates.
For the median of 2052, the author guesses that these considerations roughly cancel out, and so rounds the median for development of TAI to **2050**. A sensitivity analysis concludes that 2040 is the “most aggressive plausible median”, while the “most conservative plausible median” is 2080.
Planned opinion:
I really liked this report: it’s extremely thorough and anticipates and responds to a large number of potential reactions. I’ve made my own timelines estimate using the provided spreadsheet, and have adopted the resulting graph (with a few modifications) as my TAI timeline (which ends up with a median of ~2055). This is saying quite a lot: it’s pretty rare that a quantitative model is compelling enough that I’m inclined to only slightly edit its output, as opposed to simply using the quantitative model to inform my intuitions.
Here are the main ways in which my model is different from the one in the report:
1. Ignoring the genome anchor
I ignore the genome anchor because I don’t buy the model: even if researchers did create a very parameter-efficient model class (which seems unlikely), I would not expect the same scaling laws to apply to that model class. The report mentions that you could also interpret the genome anchor as simply providing a constraint on how many data points are needed to train long-horizon behaviors (since that’s what evolution was optimizing), but I prefer to take this as (fairly weak) evidence that informs what weights to place on short vs. medium vs. long horizons for neural nets.
2. Placing more weight on short and medium horizons relative to long horizonsI place 30% on short horizons, 40% on medium horizons, and 10% on long horizons. The report already names several reasons why we might expect the long horizon assumption to be too conservative. I agree with all of those, and have one more of my own:
If meta-learning turns out to require a huge amount of compute, we can instead directly train on some transformative task with a lower horizon. Even some of the hardest tasks like scientific R&D shouldn’t have a huge horizon: even if we assume that it takes human scientists a year to produce the equivalent of a single data point, at 40 hours a week that comes out to a horizon of 2000 subjective hours, or 7e6 seconds. This is near the beginning of the long horizon realm of 1e6-1e9 seconds and seems like a very conservative overestimate to me.
(Note that in practice I’d guess we will train something like a meta-learner, because I suspect the skill of meta-learning will not require such large average effective horizons.)
3. Reduced willingness to spend
My willingness to spend forecasts are somewhat lower: the predictions and reasoning in this report feel closer to upper bounds on how much people might spend rather than predictions of how much they will spend. Assuming we reduce the ratio of all-in project costs to final training run costs to 10x, spending $1B on a training run by 2025 would imply all-in project costs of $10B, which is ~40% of Google’s yearly R&D budget of $26B, or 10% of the budget for a 4-year project. Possibly this wouldn’t be classified as R&D, but it would also be _2% of all expenditures over 4 years_. This feels remarkably high to me for something that’s supposed to happen within 5 years; while I wouldn’t rule it out, it wouldn’t be my median prediction.
4. Accounting for challenges
While the report does talk about challenges in e.g. getting the right data and environments by the right time, I think there are a bunch of other challenges as well: for example, you need to ensure that your model is aligned, robust, and reliable (at least if you want to deploy it and get economic value from it). I do expect that these challenges will be easier than they are today, partly because more research will have been done and partly because the models themselves will be more capable.
Another example of a challenge would be PR concerns: it seems very plausible to me that there will be a backlash against transformative AI systems, that results in those systems being deployed later than we’d expect them to be according to this model.
To be more concrete, if we ignore points 1-3 and assume this is my only disagreement, then for the median of 2052, rather than assuming that reasons for optimism and pessimism approximately cancel out to yield 2050 as the median for TAI, I’d be inclined to shade upwards to 2055 or 2060 as my median for TAI.
PSA. The report includes a Colab notebook that allows you to run Ajeya’s model with your own estimates for input variables. Some of the variables are “How many FLOP/s will a transformative AI run on?”, “How many datapoints will be required to train a transformative AI?”, and “How likely are various models for transformative AI (e.g. scale up deep learning, recapitulate learning in human lifetime, recapitulate evolution)?”. If you enter your estimates, the model will calculate your personal CDF for when transformative AI arrives.
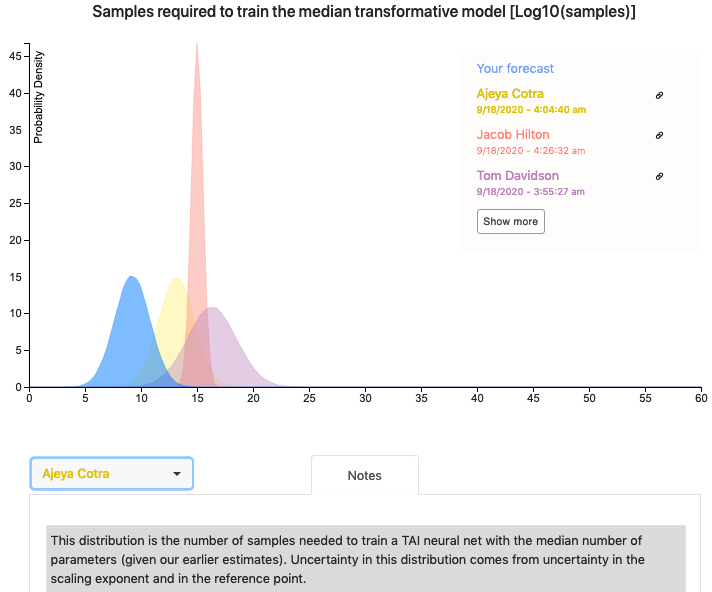
Here is a screenshot from the Colab notebook. Your distribution (“Your forecast”) is shown alongside the distributions of Ajeya, Tom Davidson (Open Philanthropy) and Jacob Hilton (OpenAI). You can also read their explanations for their distributions under “Notes”. (I work at Ought and we worked on the Elicit features in this notebook.)
Thanks for doing this, this is really good!
Some quick thoughts, will follow up later with more once I finish reading and digesting:
--I feel like it's unfair to downweight the less-compute-needed scenarios based on recent evidence, without also downweighting some of the higher-compute scenarios as well. Sure, I concede that the recent boom in deep learning is not quite as massive as one might expect if one more order of magnitude would get us to TAI. But I also think that it's a lot bigger than one might expect if fifteen more are needed! Moreover I feel that the update should be fairly small in both cases, because both updates are based on armchair speculation about what the market and capabilities landscape should look like in the years leading up to TAI. Maybe the market isn't efficient; maybe we really are in an AI overhang.
--If we are in the business of adjusting our weights for the various distributions based on recent empirical evidence (as opposed to more a priori considerations) then I feel like there are other pieces of evidence that argue for shorter timelines. For example, the GPT scaling trends seem to go somewhere really exciting if you extrapolate it four more orders of magnitude or so.
--Relatedly, GPT-3 is the most impressive model I know of so far, and it has only 1/1000th as many parameters as the human brain has synapses. I think it's not crazy to think that maybe we'll start getting some transformative shit once we have models with as many parameters as the human brain, trained for the equivalent of 30 years. Yes, this goes against the scaling laws, and yes, arguably the human brain makes use of priors and instincts baked in by evolution, etc. But still, I feel like at least a couple percentage points of probability should be added to "it'll only take a few more orders of magnitude" just in case we are wrong about the laws or their applicability. It seems overconfident not to. Maybe I just don't know enough about the scaling laws and stuff to have as much confidence in them as you do.
Thanks Daniel! Quick replies:
- On down-weighting low-end vs high-end compute levels: The reason that the down-weighting for low-end compute levels was done in a separate and explicit way was just because I think there's a structural difference between the two updates. When updating against low-end compute levels, I think it makes more sense to do that update within each hypothesis, because only some orders of magnitude are affected. To implement an "update against high-end compute levels", we can simply lower the probability we assign to high-compute hypotheses, since there is no specific reason to shave off just a few OOMs at the far right. My probability on the Evolution Anchor hypothesis is 10%, and my probability on the Long Horizon Neural Network hypothesis is 15%; this is lower than my probability on the Short Horizon Neural Network hypothesis (20%) and Medium Horizon Neural Network hypothesis (30%) because I feel that the higher-end hypotheses are less consistent with the holistic balance of evidence.
- On the GPT scaling trend: I think that the way to express the view that GPT++ would constitute TAI is to heavily weight the Short Horizon Neural Network hypothesis, potentially along with shifting and/or narrowing the range of effective horizon lengths in that bucket to be more concentrated on the low end (e.g. 0.1 to 30 subjective seconds rather than 1 to 1000 subjective seconds).
- On getting transformative abilities with 1e15 parameter models trained for 30 subjective years: I think this is pretty unlikely, but not crazy like you said; I think the way to express this view would be to up-weight the Lifetime Anchor hypothesis. My weight on it is currently 5%. Additionally, all the Neural Network hypotheses bake in substantial probability to relatively small models (e.g. 1e12 FLOP/subj sec) and scaling more shallow than we've seen demonstrated so far (e.g. an exponent of 0.25).
Thanks! Just as a heads up, I now have read it thoroughly enough that I've collected quite a few thoughts about it, and so I intend to make a post sometime in the next week or so giving my various points of disagreement and confusion, including my response to your response here. If you'd rather me do this sooner, I can hustle, and if you'd rather me wait till after the report is out, I can do that too.
Thanks! No need to wait for a more official release (that could take a long time since I'm prioritizing other projects).
One reason I put a bit more weight on short / medium horizons was that even if transformative tasks are long-horizon, you could use self-supervised pretraining to do most learning, thus reducing the long-horizon data requirements. Now that Scaling Laws for Transfer is out, we can use it to estimate how much this might help. So let's do some bogus back-of-the-envelope calculations:
We'll make the very questionable assumption that the law relating our short-horizon pretraining task and our long-horizon transformative task will still be .
Let's assume that the long-horizon transformative task has a horizon that is 7 orders of magnitude larger than the short-horizon pretraining task. (The full range is 9 orders of magnitude.) Let the from-scratch compute of a short-horizon transformative task be . Then the from-scratch compute for our long horizon task would be , if we had to train on all 1e13 data points.
Our key trick is going to be to make the model larger, and pretrain on a short-horizon task, to reduce the amount of long-horizon data we need. Suppose we multiply the model size by a factor of . We'll estimate total compute as a function of c, and then find the value that minimizes it.
Making the model bigger increases the necessary (short-horizon) pretraining data by a factor of , so pretraining compute goes up by a factor of . For transfer, goes up by a factor of .
We still want to have data points for the long-horizon transformative task. To actually get computational savings, we need to get this primarily from transfer, i.e. we have , which we can solve to get .
Then the total compute is given by .
Minimizing this gives us , in which case total compute is .
Thus, we've taken a base time of , and reduced it down to , a little over an order of magnitude speedup. This is solidly within my previous expectations (looking at my notes, I said "a couple of orders of magnitude"), so my timelines don't change much.
Some major caveats:
- The calculation is super bogus; there's no reason to expect to be the same for TAI as for finetuning code completion on text; different values could wildly change the conclusion.
- It's not clear to me that this particular scaling law should be expected to hold for such large models.
- There are lots of other reasons to prefer the short / medium horizon hypotheses (see my opinion above).
So exciting that this is finally out!!!
I haven't gotten a chance to play with the models yet, but thought it might be worth noting the ways I would change the inputs (though I haven't thought about it very carefully):
- I think I have a lot more uncertainty about neural net inference FLOP/s vs. brain FLOP/s, especially given that the brain is significantly more interconnected than the average 2020 neural net-- probably closer to 3 - 5 OOM standard deviation.
- I think I also have a bunch of uncertainty about algorithmic efficiency progress-- I could imagine e.g. that the right model would be several independent processes all of which constrain progress, so probably would make that some kind of broad distribution as well.
Thanks! I definitely agree that the proper modeling technique would involve introducing uncertainty on algorithmic progress, and that this uncertainty would be pretty wide; this is one of the most important few directions of future research (the others being better understanding effective horizon length and better narrowing model size).
In terms of uncertainty in model size, I personally find it somewhat easier to think about what the final spread should be in the training FLOP requirements distribution, since there's a fair amount of arbitrariness in how the uncertainty is apportioned between model size and scaling behavior. There's also semantic uncertainty about what it means to "condition on the hypothesis that X is the best anchor." If we're living in the world of "brain FLOP/s anchor + normal scaling behavior", then assigning a lot of weight to really small model sizes would wind up "in the territory" of the Lifetime Anchor hypothesis, and assigning a lot of weight to really large model sizes would wind up "in the territory" of the Evolution Anchor hypothesis, or go beyond the Evolution Anchor hypothesis.
I was roughly aiming for +- 5 OOM uncertainty in training FLOP requirements on top of the anchor distribution, and then apportioned uncertainty between model size and scaling behavior based on which one seemed more uncertain.
General feedback: my belief is that brain algorithms and today's deep learning models are different types of algorithms, and therefore regardless of whether TAI winds up looking like the former or the latter (or something else entirely), this type of exercise (i.e. where you match the two up along some axis) is not likely to be all that meaningful.
Having said that, I don't think the information value is literally zero, I see why someone pretty much has to do this kind of analysis, and so, might as well do the best job possible. This is a very impressive effort and I applaud it, even though I'm not personally updating on it to any appreciable extent.
I'm not seeing the merit of the genome anchor. I see how it would make sense if humans didn't learn anything over the course of their lifetime. Then all the inference-time algorithmic complexity would come from the genome, and you would need your ML process to search over a space of models that can express that complexity. However, needless to say, humans do learn things over the course of their lifetime! I feel even more strongly about that than most, but I imagine we can all agree that the inference-time algorithmic complexity of an adult brain is not limited by what's in the genome, but rather also incorporates information from self-supervised learning etc.
The opposite perspective would say: the analogy isn't between the ML trained model and the genome, but rather between the ML learning algorithm and the genome on one level, and between the ML trained model and the synapses at the other level. So, something like ML parameter count = synapse count, and meanwhile the genome size would correspond to "how complicated is the architecture and learning algorithm?"—like, add up the algorithmic complexity of backprop plus dropout regularization plus BatchNorm plus data augmentation plus xavier initialization etc. etc. Or something like that.
I think the truth is somewhere in between, but a lot closer to the synapse-anchor side (that ignores instincts) than the genome-anchor side (that ignores learning), I think...
Sorry if I'm misunderstanding or missing something, or confused.
UPDATE: Or are we supposed to imagine an RNN wherein the genomic information corresponds to the weights, and the synapse information corresponds to the hidden state activations? If so, I didn't think you could design an RNN (of the type typically used today) where the hidden state activations have many orders of magnitude more information content than the weights. Usually there are more weights than hidden state activations, right?
UPDATE 2: See my reply to this comment.
Let me try again. Maybe this will be clearer.
The paradigm of the brain is online learning. There are a "small" number of adjustable parameters on how the process is set up, and then each run is long—a billion subjective seconds. And during the run there are a "large" number of adjustable parameters that get adjusted. Almost all the information content comes within a single run.
The paradigm of today's popular ML approaches is train-then-infer. There are a "large" number of adjustable parameters, which are adjusted over the course of an extremely large number of extremely short runs. Almost all the information content comes from the training process, not within the run. Meanwhile, sometimes people do multiple model-training runs with different hyperparameters—hyperparameters are a "small" number of adjustable parameters that sit outside the gradient-descent training loop.
I think the appropriate analogy is:
- (A) Brain: One (billion-subjective-second) run ↔ ML: One gradient-descent model training
- (B) Brain: Adjustable parameters on the genome ↔ ML: Hyperparameters
- (C) Brain: Settings of synapses (or potential synapses) in a particular adult ↔ ML: parameter settings of a fully-trained model
This seems to work reasonably well all around: (A) takes a long time and involves a lot of information content in the developed "intelligence", (B) is a handful of (perhaps human-interpretable) parameters, (C) is the final "intelligence" that you wind up wanting to deploy.
So again I would analogize one run of the online-learning paradigm with one training of today's popular ML approaches. Then I would try to guess how many runs of online-learning you need, and I would guess 10-100, not based on anything in particular, but you can get a better number by looking into the extent to which people need to play with hyperparameters in their ML training, which is "not much if it's very important not to".
Sure, you can do a boil-the-oceans automated hyperparameter search, but in the biggest projects where you have no compute to spare, they can't do that. Instead, you sit and think about the hyperparameters, you do smaller-scale studies, you try to carefully diagnose the results of each training, etc. etc. Like, GPT-3 only did one training of their largest model, I believe—they worked hard to figure out good hyperparameter settings by extrapolating from smaller studies.
...Whereas it seems that the report is doing a different analogy:
- (A) Brain: One (billion-subjective-second) run ↔ ML: One run during training (one play of an Atari game etc.)
- (B) Brain: Adjustable parameters on the genome ↔ ML: Learnable parameters in the model
- (C) Brain: Many (billion-subjective-second) runs ↔ ML: One model-training session
I think that analogy is much worse than the one I proposed. You're mixing short tests with long-calculations-that-involve-a-ton-of-learning, you're mixing human tweaking of understandable parameters with gradient descent, etc.
To be clear, I don't think my proposed analogy is perfect, because I think that brain algorithms are rather different than today's ML algorithms. But I think it's a lot better than what's there now, and maybe it's the best you can do without getting into highly speculative and controversial inside-view-about-brain-algorithms stuff.
I could be wrong or confused :-)
Potentially worth noting that if you add the lifetime anchor to the genome anchor, you most likely get ~the genome anchor.
Ajeya's timelines report is the best thing that's ever been written about AI timelines imo. Whenever people ask me for my views on timelines, I go through the following mini-flowchart:
1. Have you read Ajeya's report?
--If yes, launch into a conversation about the distribution over 2020's training compute and explain why I think the distribution should be substantially to the left, why I worry it might shift leftward faster than she projects, and why I think we should use it to forecast AI-PONR instead of TAI.
--If no, launch into a conversation about Ajeya's framework and why it's the best and why all discussion of AI timelines should begin there.
So, why do I think it's the best? Well, there's a lot to say on the subject, but, in a nutshell: Ajeya's framework is to AI forecasting what actual climate models are to climate change forecasting (by contrast with lower-tier methods such as "Just look at the time series of temperature over time / AI performance over time and extrapolate" and "Make a list of factors that might push the temperature up or down in the future / make AI progress harder or easier," and of course the classic "poll a bunch of people with vaguely related credentials."
There's something else which is harder to convey... I want to say Ajeya's model doesn't actually assume anything, or maybe it makes only a few very plausible assumptions. This is underappreciated, I think. People will say e.g. "I think data is the bottleneck, not compute." But Ajeya's model doesn't assume otherwise! If you think data is the bottleneck, then the model is more difficult for you to use and will give more boring outputs, but you can still use it. (Concretely, you'd have 2020's training compute requirements distribution with lots of probability mass way to the right, and then rather than say the distribution shifts to the left at a rate of about one OOM a decade, you'd input whatever trend you think characterizes the likely improvements in data gathering.)
The upshot of this is that I think a lot of people are making a mistake when they treat Ajeya's framework as just another model to foxily aggregate over. "When I think through Ajeya's model, I get X timelines, but then when I extrapolate out GWP trends I get Y timelines, so I'm going to go with (X+Y)/2." I think instead everyone's timelines should be derived from variations on Ajeya's model, with extensions to account for things deemed important (like data collection progress) and tweaks upwards or downwards to account for the rest of the stuff not modelled.
From Part 4 of the report:
Nonetheless, this cursory examination makes me believe that it’s fairly unlikely that my current estimates are off by several orders of magnitude. If the amount of computation required to train a transformative model were (say) ~10 OOM larger than my estimates, that would imply that current ML models should be nowhere near the abilities of even small insects such as fruit flies (whose brains are 100 times smaller than bee brains). On the other hand, if the amount of computation required to train a transformative model were ~10 OOM smaller than my estimate, our models should be as capable as primates or large birds (and transformative AI may well have been affordable for several years).
I'm not sure I totally follow why this should be true-- is this predicated on already assuming that the computation to train a neural network equivalent to a brain with N neurons scales in some particular way with respect to N?
Yes, it's assuming the scaling behavior follows the probability distributions laid out in Part 2, and then asking whether conditional on that the model size requirements could be off by a large amount.
Thanks for sharing this draft! I'm going to try to make lots of different comments as I go along, rather than one huge comment.
[edit: page 10 calls this the "most important thread of further research"; the downside of writing as I go! For posterity's sake, I'll leave the comment.]
Pages 8 and 9 of part 1 talk about "effective horizon length", and make the claim:
Prima facie, I would expect that if we modify an ML problem so that effective horizon length is doubled (i.e, it takes twice as much data on average to reach a certain level of confidence about whether a perturbation to the model improved performance), the total training data required to train a model would also double. That is, I would expect training data requirements to scale linearly with effective horizon length as I have defined it.
I'm curious where 'linearly' came from; my sense is that "effective horizon length" is the equivalent of "optimal batch size", which I would have expected to be a weirder function of training data size than 'linear'. I don't have a great handle on the ML theory here, tho, and it might be substantially different between classification (where I can make batch-of-the-envelope estimates for this sort of thing) and RL (where it feels like it's a component of a much trickier system with harder-to-predict connections).
Quite possibly you talked with some ML experts and their sense was "linearly", and it makes sense to roll with that; it also seems quite possible that the thing to do here is have uncertainty over functional forms. That is, maybe the effective horizon scales linearly, or maybe it scales exponentially, or maybe it scales logarithmically, or inverse square root, or whatever. This would help double-check that the assumption of linearity isn't doing significant work, and if it is, point to a potentially promising avenue of theoretical ML research.
[As a broader point, I think this 'functional form uncertainty' is a big deal for my timelines estimates. A lot of people (rightfully!) dismissed the standard RL algorithms of 5 years ago for making AGI because of exponential training data requirements, but my sense is that further algorithmic improvement is mostly not "it's 10% faster" but "the base of the exponent is smaller" or "it's no longer exponential.", which might change whether or not it makes sense to dismiss it.]
Thanks! Agree that functional form uncertainty is a big deal here; I think that implicitly this uncertainty is causing me to up-weight Short Horizon Neural Network more than I otherwise would, and also up-weight "Larger than all hypotheses" more than I otherwise would.
With that said, I do predict that in clean artificial cases (which may or may not be relevant), we could demonstrate linear scaling. E.g., consider the case of inserting a frame of static or a blank screen in between every normal frame of an Atari game or StarCraft game -- I'd expect that modifying the games in this way would straightforwardly double training computation requirements.
I implemented the model for 2020 compute requirements in Guesstimate here. It doesn't do anything that the notebook can't do (and it can't do the update against currently affordable compute), but I find the graphical structure very helpful for understanding how it works (especially with arrows turned on in the "View" menu).
David Roodman put together a Guesstimate model that some people might find helpful: https://www.getguesstimate.com/models/18944
I am organizing a reading group for this report next Tuesday in case you (or anyone else) wants to show up:
If we use median AI timings, we will be 50 per cent dead before that moment. May be it will be useful different measure, like 10 per cent of TAI, before which our protective measures should be prepared?
Also, this model contradicts naive model of GPT growth in which the number of parameters has been growing 2 orders of magnitude a year last couple of years, and if this trend continues, it could reach human level of 100 trillion parameters in 2 years.
Thanks!
I agree that full distribution information is very valuable, although I consider medians to be important as well. The spreadsheet linked in the report provides the full distribution implied by my views for the probability that the amount of computation required to train a transformative model is affordable, although it requires some judgment to translate that into P(TAI), because there may be other bottlenecks besides computation and there may be other paths to TAI besides training a transformative model. I'd say it implies somewhere between 2031 and 2036 is the year by which there is a 10% chance of TAI.
As I said in a reply to Daniel above, the way to express the view that a brain-sized GPT model would constitute TAI is to assign a lot of weight to the Short Horizon Neural Network hypothesis, potentially along with shifting narrowing the effective horizon length. I think this is plausible, but don't believe we should have a high probability on this because I expect on priors that we would need longer effective horizon lengths than GPT-3, and I don't think that evidence from the GPT-3 paper or follow on papers have provided clear evidence to the contrary.
In my best guess inputs, I assign a 25% probability collectively to the Short Horizon Neural Network and Lifetime Anchor hypotheses; in my aggressive inputs I assign 50% probability to these two hypotheses collectively. In both cases, probabilities are smoothed to a significant extent because of uncertainty in model size requirements and scaling, with substantial weight on smaller-than-brain-sized models and larger-than-brain-sized models.
I saw a presentation covering a bunch of this back in February, and the graphs I found most informative were those showing the training flop distributions before updating against already-achievable levels. There is one graph along these lines on page 13 in part 1 in the google docs, but it doesn't show the combined distribution without the update against already achievable flops.
Am I correct in remembering that the combined distribution before that update was distinctly bimodal? That was one of my main takeaways from the presentation, and I want to make sure I'm remembering it correctly.
Hi John, I think I remember that presentation -- the reason the graph there was quite bimodal is because the Lifetime Anchor I was using at the time was simply assuming ~1x human lifetime levels of computation. In the current model, I'm assuming ~1000x human lifetime levels of computation, because ~1x seemed like a much less likely version of that anchor. The code in the quantitative model will let you see the untruncated version of the distribution, and it looks a lot more smooth now, though still a modest bump.
Also, apologies for such a late reply, I don't get email notifications for comments and haven't been checking regularly!
Some thoughts:
-
The development of transformative AI may involve a feedback loop in which we train ML models that help us train better ML models and so on (e.g. using approaches like neural architecture search which seems to be getting increasingly popular in recent years). There is nothing equivalent to such a feedback loop in biological evolution (animals don't use their problem-solving capabilities to make evolution more efficient). Does your analysis assume there won't be such a feedback loop (or at least not one that has a large influence on timelines)? Consider adding to the report a discussion about this topic (sorry if it's already there and I missed it).
-
Part of the Neural Network hypothesis is the proposition that "a transformative model would perform roughly as many FLOP / subj sec as the human brain". It seems to me worthwhile to investigate this proposition further. Human evolution corresponds to a search over a tiny subset of all possible computing machines. Why should we expect that a different search algorithm over an entirely different subset of computing machines would yield systems (with certain capabilities) that use a similar amount of compute? One might pursue an empirical approach for investigating this topic, e.g. by comparing two algorithms for searching over a space of models, where one is some common supervised learning algorithm, and the other is some evolutionary computation algorithm.
In a separate comment (under this one) I attempt to describe a more thorough and formal way of thinking about this topic.
-
Regarding methods that involve adjusting variables according to properties of 2020 algorithms (or the models trained by them): It would be interesting to try to apply the same methods with respect to earlier points in time (e.g. as if you were writing the report back in 1998/2012/2015 when LeNet-5/AlexNet/DQN were introduced, respectively). To what extent would the results be consistent with the 2020 analysis?
Let and be two optimization algorithms, each searching over some set of programs. Let be some evaluation metric over programs such that is our evaluation of program , for the purpose of comparing a program found by to a program found by . For example, can be defined as a subjective impressiveness metric as judged by a human.
Intuitive definition: Suppose we plot a curve for each optimization algorithm such that the x-axis is the inference compute of a yielded program and the y-axis is our evaluation value of that program. If the curves of and are similar up to scaling along the x-axis, then we say that and are similarly-scaling w.r.t inference compute, or SSIC for short.
Formal definition: Let and be optimization algorithms and let be an evaluation function over programs. Let us denote with the program that finds when it uses flops (which would correspond to the training compute if is an ML algorithms). Let us denote with the amount of compute that program uses. We say that and are SSIC with respect to if for any ,,, such that , if then .
I think the report draft implicitly uses the assumption that human evolution and the first ML algorithm that will result in TAI are SSIC (with respect to a relevant ). It may be beneficial to discuss this assumption in the report. Clearly, not all pairs of optimization algorithms are SSIC (e.g. consider a pure random search + any optimization algorithm). Under what conditions should we expect a pair of optimization algorithms to be SSIC with respect to a given ?
Maybe that question should be investigated empirically, by looking at pairs of optimization algorithms, were one is a popular ML algorithm and the other is some evolutionary computation algorithm (searching over a very different model space), and checking to what extent the two algorithms are SSIC.
Part 1 page 15 talks about "spending on computation", and assumes spending saturates at 1% of the GDP of the largest country. This seems potentially odd to me; quite possibly the spending will be done by multinational corporations that view themselves as more "global" than "American" or "British" or whatever, and whose fortunes are more tied to the global economy than to the national economy. At most this gives you a factor of 2-3 doublings, but that's still 4-6 years on a 2-year doubling time.
Overall I'm not sure how much to believe this hypothesis; my mainline prediction is that corporations grow in power and rootlessness compared to nation-states, but it also seems likely that bits of the global economy will fracture / there will be a push to decentralization over centralization, where (say) Alphabet is more like "global excluding China, where Baidu is supreme" than it is "global." In that world, I think you still see approximately a 4x increase.
I also don't have a great sense how we should expect the 'ability to fund large projects' to compare between the governments of the past and the megacorps of the future; it seems quite plausible to me that Alphabet, without pressure to do welfare spending / fund the military / etc. could put a much larger fraction of its resources towards building TAI, but also presumably this means Alphabet has many fewer resources than the economy as a whole (because there still will be welfare spending and military funding and so on), and on net this probably works out to 1% of total gdp available for megaprojects.
Yeah, I considered pegging spending to a fraction of GWP instead of a fraction of GDP, but found that when I did this I wanted to push the fraction down because I felt that even though companies are getting increasingly globalized, coordination at the world-scale would probably still be thinner than coordination at the scale of something nation-sized (even if it's not actually a literal nation). Ultimately, I just went with GDP because there are more reference points for it.
I feel pretty uncertain about this though, and think there's a lot of room for a more detailed inside-view projection on willingness-to-spend by a firm. We could calculate this by making assumptions about the global surplus created by a transformative model (easily calculable from the definition), the amount of that profit that a firm would capture if it trained a transformative model, and the size of the frontier firm over time (which could be pegged to the global economy or potentially pegged to estimates of profits from training smaller models). We could then back out what a rational firm should be willing to invest.
We could then back out what a rational firm should be willing to invest.
This makes sense, altho I note that I expect the funding here to quite plausibly be 'irrational.' For example, some substantial fraction of Microsoft's value captured is going to global development in a way that seems unlikely to make sense from Microsoft's bottom line (because Microsoft enriched one of its owners, who then decided to deploy those riches for global development). If building TAI comes out of the 'altruism' or 'exploration' budget instead of the 'we expect this to pay back on schedule' budget, you could see more investment than that last category would justify.
Yeah, I agree there is room for spending to be "irrational", though I would guess this is more likely in the direction of spending less than the "rational" amount rather than more, because developing TAI could be unprecedentedly profitable and companies' spending may be limited by capital constraints.
From the draft (Part 3):
I think it is unlikely that the amount of computation that would be required to train a transformative model is in the range of AlphaStar or a few orders of magnitude more -- if that were feasible, I would expect some company to have already trained a transformative model, or at least to have trained models that have already had massive economic impact. To loosely approximate a Bayesian update based on the evidence from this “efficient markets” argument, I truncate and renormalize all the hypothesis probability distributions:
[...]
Can you give some concrete examples of models with massive economic impact that we don't currently see but should expect to see before affordable levels of computation are sufficient for training transformative models?
A simple, well-funded example is autonomous vehicles, which have spent considerably more than the training budget of AlphaStar, and are not there yet.
I am aware of other examples that do seem to be happening, but I'm not sure what the cutoff for 'massive' should be. For example, a 'call center bot' is moderately valuable (while not nearly as transformative as autonomous vehicles), and I believe there are many different companies attempting to do something like that, altho I don't know how their total ML expenditure compared to AlphaStar's. (The company I'm most familiar with in this space, Apprente, got acquired by McDonalds last year, who I presume is mostly interested in the ability to automate drive-thru orders.)
Another example that seems relevant to me is robotic hands (plus image classification) at sufficient level that warehouse pickers could be replaced by robots.
An important question IMO is whether or not those massive expenditures are for making large neural nets, as opposed to training them for a long time or having loads of them in parallel or something else entirely like researcher salaries.
My guess is that Tesla, Waymo, etc. use neural nets 2+ orders of magnitude smaller than GPT-3 (as measured by parameter count.) Ditto for call center automation, robots, etc.
There are some limited sensitivity analysis in the "Conservative and aggressive estimates" section of part 4.
I'd prefer if people didn't share it widely in a low-bandwidth way (e.g., just posting key graphics on Facebook or Twitter) since the conclusions don't reflect Open Phil's "institutional view" yet, and there may well be some errors in the report.
Isn't that in contradiction with posting it to LW (by crossposting)? I mean, it's in free access for everyone, so anyone that wants to share it can find it.
I expect the examples Ajeya has in mind are more like sharing one-line summaries in places that tend to be positively selected for virality and anti-selected for nuance (like tweets), but that substantive engagement by individuals here or in longer posts will be much appreciated.
I'm assuming part of the point is the LW crosspost still buries things in a hard-to-navigate google doc, which prevents it from easily getting cited or going viral, and Ajeya is asking/hoping for trust that they can get the benefit of some additional review from a wider variety of sources.
Hi all, I've been working on some AI forecasting research and have prepared a draft report on timelines to transformative AI. I would love feedback from this community, so I've made the report viewable in a Google Drive folder here.
With that said, most of my focus so far has been on the high-level structure of the framework, so the particular quantitative estimates are very much in flux and many input parameters aren't pinned down well -- I wrote the bulk of this report before July and have received feedback since then that I haven't fully incorporated yet. I'd prefer if people didn't share it widely in a low-bandwidth way (e.g., just posting key graphics on Facebook or Twitter) since the conclusions don't reflect Open Phil's "institutional view" yet, and there may well be some errors in the report.
The report includes a quantitative model written in Python. Ought has worked with me to integrate their forecasting platform Elicit into the model so that you can see other people's forecasts for various parameters. If you have questions or feedback about the Elicit integration, feel free to reach out to elicit@ought.org.
Looking forward to hearing people's thoughts!